Примеры
Пример 1: фраза «напряжение в сети должно быть 220 ± 4,5 вольт» означает, что напряжение должно быть в диапазоне от 215,5 до 224,5 вольт.
Пример 2, где символ «плюс-минус» надо понимать буквально, как указание альтернативы из двух вариантов — известная формула для вычисления двух корней квадратного уравнения \displaystyle{ ax^2 + bx + c = 0 }:
- \displaystyle{ \displaystyle x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}. }
Эта формула — компактная запись, объединяющая формулы для первого и второго корня:
- \displaystyle{ \displaystyle x_1 = \frac{-b + \sqrt {b^2-4ac}}{2a}; \quad x_2 = \frac{-b — \sqrt {b^2-4ac}}{2a} }
Пример 3, аналогичный второму, тригонометрический:
- \displaystyle{ \sin(x \pm y) = \sin(x) \cos(y) \pm \cos(x) \sin(y) }
Пример 4. Здесь истолкование символа плюс-минус иное: надо выбрать знак одночлена в зависимости от его номера в ряду:
- \displaystyle{ \sin\left( x \right) = x — \frac{x^3}{3!} + \frac{x^5}{5!} — \frac{x^7}{7!} + \cdots \pm \frac{1}{(2n+1)!} x^{2n+1} + \cdots }
Значение символа в программировании
Символы в программировании играют важную роль, они используются для создания и написания кода. Каждый символ имеет свое значение и выполняет свою задачу. Например, символы «;» или «{» являются разделителями и используются для разделения кода на отдельные строки. Символы «+» и «-» используются для выполнения арифметических операций.
Также существуют специальные символы, которые используются для кодирования текста и передачи информации. Например, символ «\» используется для экранирования других символов, чтобы они были интерпретированы правильно. Символы «» используются для обозначения HTML-тегов, которые используются для создания веб-страниц.
Кроме того, в программировании используются символы для создания условий и логических выражений. Например, символы «&&» и «||» используются для создания логических операций «И» и «ИЛИ». Символ «!» используется для отрицания выражения.
Использование символов в программировании требует точного знания и понимания их значения
Важно не пропустить ни один символ, так как это может повлиять на правильность и работоспособность программы
Encodings[edit]
- In Unicode: U+00B1 ± PLUS-MINUS SIGN
- In ISO 8859-1, -7, -8, -9, -13, -15, and -16, the plus–minus symbol is code 0xB1hex. This location was copied to Unicode.
- The symbol also has a HTML entity representations of , , and .
- The rarer minus–plus sign is not generally found in legacy encodings, but is available in Unicode as U+2213 ∓ MINUS-OR-PLUS SIGN so can be used in HTML using or .
- In TeX ‘plus-or-minus’ and ‘minus-or-plus’ symbols are denoted and , respectively.
- Although these characters may also be produced using underlining or overlining + symbol ( + or + ), this is deprecated because the formatting may be stripped at a later date, changing the meaning. It also makes the meaning less accessible to blind users with screen readers.
Typingedit
- Windows: Alt+241 or Alt+177 (numbers typed on the numeric keypad).
- Macintosh: ⌥ Option+⇧ Shift+= (equal sign on the non-numeric keypad).
- Unix-like systems: Compose,+,- or ⇧ Shift+Ctrl+uB1space (second works on Chromebook)
- In the Vim text editor (in Insert mode): Ctrl+k +- or Ctrl+v 177 or Ctrl+v x B1 or Ctrl+v u B1
- AutoCAD shortcut string:
Применение в задачах
Понятие «плюс на минус» широко используется в математических задачах, особенно в финансовых расчетах. Например, предположим, что у вас есть 100 долларов, который вы хотите вложить под 3% годовых на 5 лет. В этом случае соответствующая формула будет выглядеть как:
100 + (100 x 0,03 x 5) = 115 долларов.
Таким образом, вы получите 15 долларов бонуса за плюс на минус, что означает, что вы получаете проценты как на ваш первоначальный вклад, так и на процент, который заработал этот вклад.
Кроме того, плюс на минус используется для описания изменений в показателях. Например, если скорость автомобиля увеличивается на 20% в первый час, а затем на 10% во второй час, то скорость автомобиля будет выражена как:
100% + 20% + 10% = 130%.
Это означает, что скорость автомобиля увеличилась на 30%, а не на 20% или 10%.
В целом, плюс на минус — это важное математическое понятие, которое широко применяется в различных областях, таких как финансы, экономика, наука и технологии. Это понятие помогает описать различные виды изменений и расчетов, что делает его необходимым для понимания и применения в реальной жизни
Добавление знака «плюс минус» через раздел «Символ»
1. Кликните в том месте страницы, где должен находиться знак “плюс минус”, и переключитесь на вкладку “Вставка” на панели быстрого доступа.
2. Нажмите на кнопку “Символ” (группа инструментов “Символы”), в выпадающем меню которой выберите “Другие символы”.
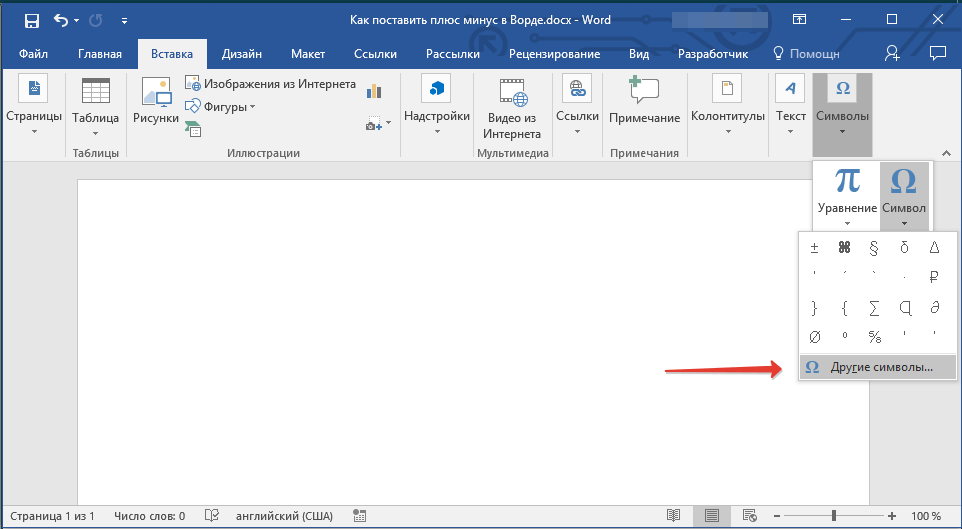
3. Убедитесь в том, что в открывшемся диалоговом окне в разделе “Шрифт” установлен параметр “Обычный текст”. В разделе “Набор” выберите “Дополнительная латиница-1”.
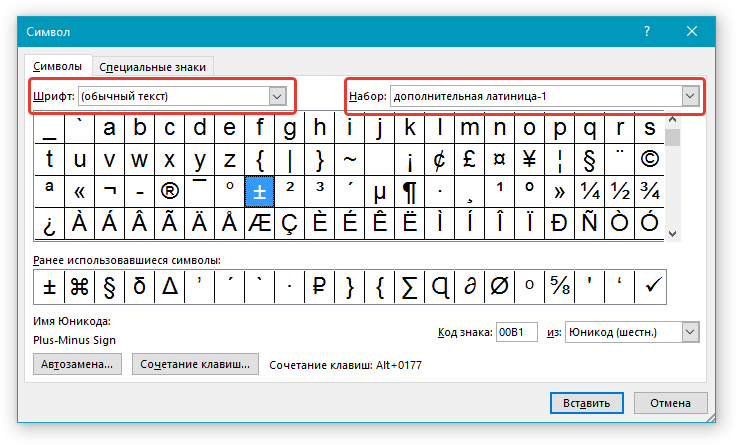
4. В появившемся списке символов найдите “плюс минус”, выберите его и нажмите “Вставить”.
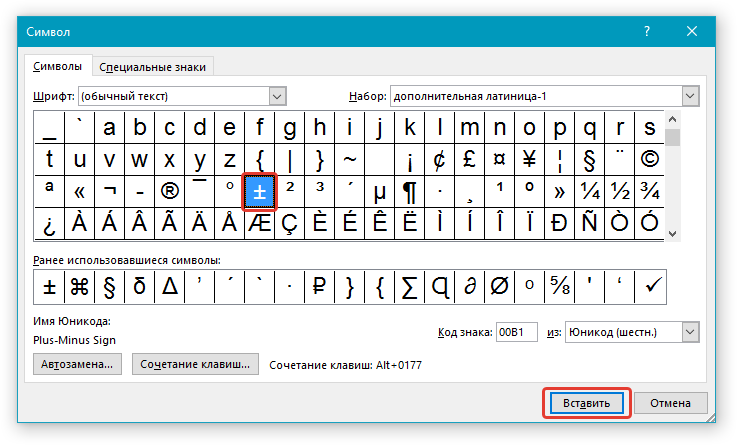
5. Закройте диалоговое окно, знак “плюс минус” появится на странице.
Урок: Вставка знака умножения в Word
История появления символа
Символ «Плюс в кружочке» (+), который мы используем в математике, был введен в употребление примерно в 1555 году германским математиком Иоганном Видманом (Johann Widmann). Он использовал этот символ для обозначения сложения и вычитания чисел в своей книге «Mercantile Arithmetic». В то время он обозначал его как две латинские буквы «p» и «m», расположенные над уровнем.
Впервые символ «+», который мы знаем сегодня, был применен в работах английского математика Роберта Рекорда (Robert Recorde) в 1557 году. Рекорд использовал этот символ в своей книге “The Whetstone of Witte”, где он даёт определения для разных математических операций.
Начиная с 17 века этот математический символ стал все более популярным в Европе и Америке. Он также был стандартизирован в Германии в 1817 году и в России в 1835 году.
В настоящее время символ «Плюс в кружочке» является принятым обозначением для сложения в математике, физике, инженерии и других науках, а также в обычной жизни для обозначения увеличения чего-либо на определенное количество.
Кроме того, символ «+» также используется в программировании и информатике для обозначения операции сложения, а также для объединения строк и списков.
- Применение символа «Плюс в кружочке»:
- Математика — операция сложения
- Физика — обозначение полярности заряда
- Инженерия — обозначение единицы измерения усилия
- Программирование — операция сложения чисел, объединение строк и списков
- Обычная жизнь — обозначение увеличения чего-либо на определенное количество
Минус в компьютерном наборе[править | править код]
Исторически знак дефиса использовался в компьютерном наборе вместо минуса и тире ввиду отсутствия отдельных клавиш для последних. В языках программирования эти символы по‑прежнему не различаются (так как обычно для служебных целей используются только символы ASCII), но при качественном наборе текстов следует различать дефис (‐), минус (−), короткое тире (–) и длинное тире (—).
В Юникоде знак минуса присутствует начиная с версии 1.0.0 в блоке Математические операторы (англ. Mathematical Operators) под шестнадцатеричным кодом 2212 и называется minus sign. В HTML имеет мнемонику .
Символы вероятности и статистики
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ⋂ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ⋂ B ) = 0,5 |
| P ( A ⋃ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ⋃ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( x макс + x мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Примеры
Чтобы лучше понять, почему «плюс» на «минус» дает «минус», рассмотрим несколько примеров.
Пример 1: Вычитание
Когда мы вычитаем одно число из другого, мы фактически складываем первое число с отрицательным вторым числом. Например, 5 — 3 = 5 + (-3) = 2. В этом случае, «плюс» на «минус» дает «минус», потому что мы складываем положительное число с отрицательным числом.
Пример 2: Умножение
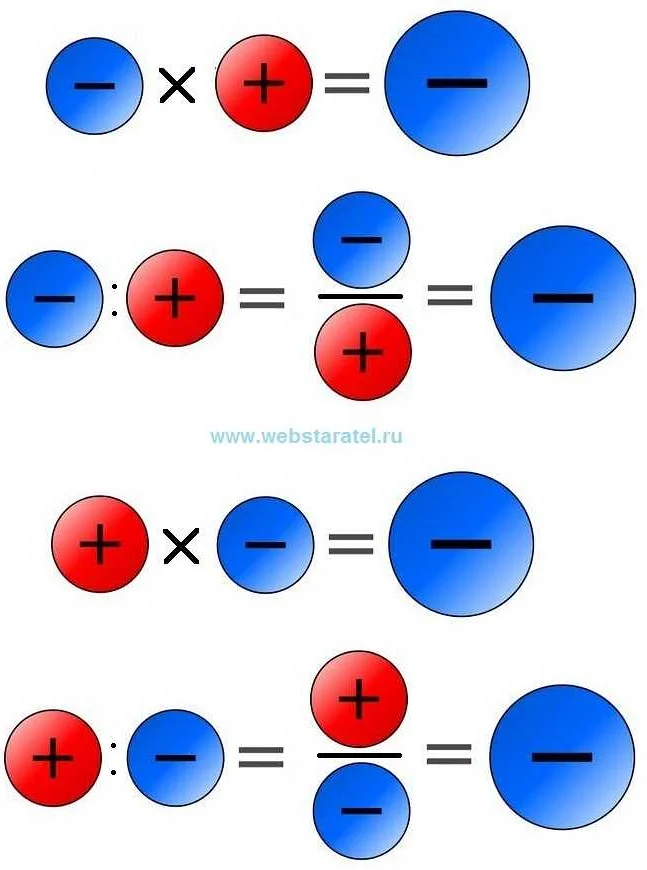
При умножении двух чисел, знак результата зависит от знаков множителей. Если оба множителя положительные или оба отрицательные, то результат будет положительным. Если один множитель положительный, а другой отрицательный, то результат будет отрицательным. Например, 2 * (-3) = -6. В этом случае, «плюс» на «минус» дает «минус», потому что один множитель положительный, а другой отрицательный.
Пример 3: Деление
При делении двух чисел, знак результата также зависит от знаков делимого и делителя. Если оба числа положительные или оба отрицательные, то результат будет положительным. Если одно число положительное, а другое отрицательное, то результат будет отрицательным. Например, 6 / (-2) = -3. В этом случае, «плюс» на «минус» дает «минус», потому что делимое положительное, а делитель отрицательный.
Пример 4: Сложение
При сложении двух чисел, знак результата зависит от знаков слагаемых. Если оба слагаемых положительные или оба отрицательные, то результат будет положительным. Если одно слагаемое положительное, а другое отрицательное, то результат будет зависеть от их абсолютных значений. Например, 2 + (-3) = -1. В этом случае, «плюс» на «минус» дает «минус», потому что одно слагаемое положительное, а другое отрицательное.
Таким образом, знак результата математических операций зависит от знаков исходных чисел и правил, которые определяют знак результата в каждом случае. Понимание этих правил поможет лучше понять, почему «плюс» на «минус» дает «минус».
| Операция | Правило | Пример |
|---|---|---|
| Вычитание | Вычитание — это просто сложение с отрицательным числом. | 5 — 3 = 5 + (-3) = 2 |
| Умножение | При умножении двух чисел, знак результата зависит от знаков множителей. | 2 * (-3) = -6 |
| Деление | При делении двух чисел, знак результата также зависит от знаков делимого и делителя. | 6 / (-2) = -3 |
| Сложение | При сложении двух чисел, знак результата зависит от знаков слагаемых. | 2 + (-3) = -1 |
Что такое математический язык
Языком называют систему общения с использованием звуков и условных символов в устной и письменной формах.
Математические обозначения служат универсальной единицей для обмена информацией между научными работниками разных сфер.
Область применения специфических математических обозначений включает в себя сферы физики, информатики, экономики и инженерии. И те области человеческой деятельности, где присутствуют математические модели.
Естественный язык служит основой формирования структуры математического языка. Многие символы заимствованы из латинского и греческого языков. Их значение интерпретируется избранной формой, типом и положением. В некоторых случаях играет роль цветопередача буквенных обозначений.
Математические знаки и символы собирают в формулы.
Выделяют словесные и символьные формулы.
Математическая формула или форма — комбинация математических знаков, с помощью которых записывают утверждения.
При написании формул используют условные обозначения — числа и буквы, специальные знаки и символы.
Формы записи утверждений бывают истинные и ложные. Смысл формул зависит от значения входящих в них переменных.
Развитие математической символики связано с общим развитием понятийного ряда и методов математики. Введение специальных обозначений началось с цифр, которые заменили зарубки, черточки, узелки в условиях обмена информационными сообщениями количественного характера.
Считают, что первые математические знаки появились у греческих геометров. Евклид использовал буквы для обозначения, например, конечной и начальной точек отрезка.
Буквенные изображения в качестве замены чисел для создания универсальных утверждений возникают в результате освобождения алгебра от геометрической формы.
В XVI веке Ф. Виет использовал буквы для замены чисел.
Создание современной символики относят к XVII веку.
Помимо индо-арабских цифр и букв греческого и латинского алфавитов, математический язык использует множество символов, которые изобретены за последние несколько столетий.
Преимущества использования математического языка заключаются в его:
- компактности;
- однозначности толкования;
- легкости преобразования.
Знак плюс в еврейской культуре
Еврейская традиция восходит по крайней мере до XIX — го века, чтобы написать более с использованием в качестве символа T восстанавливается. Эта практика была принята в израильских школах в 1940-х годах и остается в силе в большинстве начальных школ, в том числе секуляризованных, но в средних школах такая практика становится все реже. Эта практика также встречается в некоторых книгах, написанных религиозными авторами, но в большинстве книг для взрослых используется международный символ + . Обычное объяснение этой практики состоит в том, что она избегает написания символа +, который выглядит как христианский крест . Шрифты Unicode кодируют этот символ U + FB29, который представляет собой еврейскую букву ﬩, заменяющую знак плюса. Этот знак также используется на кнопках управления пассажирским сиденьем израильской авиакомпании El Al .
Объяснение правил
Почему при сложении чисел с разными знаками результат может быть отрицательным? Чтобы понять это, нужно вспомнить правила сложения чисел с разными знаками.
Правило 1: Если складываемые числа имеют одинаковый знак, то складываем их абсолютные значения и результату присваиваем знак этих чисел.
Пример: (-3) + (-5) = -(3+5) = -8
Правило 2: Если складываемые числа имеют разный знак, то вычитаем из большего по модулю меньшее по модулю и результату присваиваем знак большего числа.
Пример: (-3) + 5 = 5 — 3 = 2 (знак числа 5)
Теперь рассмотрим пример: (-3) + (-5). Согласно правилу 1, мы должны сложить абсолютные значения чисел и присвоить результату знак этих чисел. Абсолютные значения чисел 3 и 5 равны 3 и 5 соответственно. Следовательно, (-3) + (-5) = -(3+5) = -8.
Аналогично, рассмотрим пример: 5 + (-3). Согласно правилу 2, мы должны вычесть из большего по модулю меньшее по модулю и присвоить результату знак большего числа. Абсолютные значения чисел 5 и 3 равны 5 и 3 соответственно. Следовательно, 5 + (-3) = 5 — 3 = 2 (знак числа 5).
Таким образом, при сложении чисел с разными знаками результат может быть отрицательным, если большее по модулю число имеет отрицательный знак.
| Первое число | Второе число | Результат |
|---|---|---|
| 3 | 5 | 8 |
| -3 | -5 | -8 |
| 5 | -3 | 2 |
| -5 | 3 | -2 |
Таким образом, при сложении чисел с разными знаками результат может быть отрицательным, если большее по модулю число имеет отрицательный знак.
Кодировки
- В Unicode: U + 00B1 ± ЗНАК ПЛЮС-МИНУС
- В ISO 8859-1, -7, -8, -9, -13, -15, и -16, символ плюс – минус — это код 0xB1шестнадцатеричный. Это местоположение было скопировано в Unicode.
- Символ также имеет HTML-объект представления и .
- Более редкий знак минус – плюс обычно не встречается в устаревших кодировках, но доступен в Unicode как U + 2213 ∓ ЗНАК МИНУС-ИЛИ-ПЛЮС поэтому можно использовать в HTML, используя или .
- В TeX обозначаются символы «плюс-минус» и «минус-плюс». и соответственно.
- Хотя эти символы также могут быть созданы с использованием подчеркивания или перекрытия + символ (+ или + ), это не рекомендуется, потому что форматирование может быть удалено позже, изменив значение. Это также делает смысл менее доступным для слепых пользователей с программы чтения с экрана.
Значение символа в теории множеств
Значение символа «плюс в кружочке» в математике связано с теорией множеств. В этой теории «плюс в кружочке» используется для обозначения операции объединения множеств, то есть для объединения всех элементов двух или более множеств. Например, объединение множеств А и В обозначается как А ∪ В.
Использование этих символов в теории множеств позволяет решать различные математические задачи и проблемы, связанные с работой с наборами объектов. Также теория множеств является важным инструментом во многих областях математики, информатики и теоретической физики.
Применение символа «плюс в кружочке» и других символов теории множеств требует от математиков и информатиков глубокого знания теории множеств и умения правильно использовать эти символы в своих вычислениях и исследованиях.
Плюс на минус
Плюс на минус — это математическая операция, при которой к положительному числу прибавляется отрицательное число или наоборот: отрицательное число вычитается из положительного.
В результате операции плюс на минус мы получаем отрицательное число. Например, 5 + (-3) = 2, а (-7) + 2 = (-5).
Плюс на минус используется во многих математических и физических задачах, например, при расчете скорости и ускорения, при вычислении расстояния между двумя точками на координатной плоскости или при определении количества товара на складе после возврата покупателем.
- Пример 1: Если у вас есть $10, а вы потратили $12, то ваш баланс -$2.
- Пример 2: Если Вася купил 2 кг яблок за $5, а Петя продал ему 1 кг за $3, то у Васи осталось 1 кг яблок и -$2 на счету.
ОперацияПриоритет
| Скобки | Высший |
| Умножение и деление | Средний |
| Плюс и минус | Низкий |
Кодировка
| Символ | Код вЮникоде | Названиев Юникоде | Название | HTMLшестн. | HTMLдесят. | HTMLобозн. |
|---|---|---|---|---|---|---|
| \displaystyle{ \pm } | U+00B1 | Plus-minus sign | Символ плюс-минус | ± | ± | ± |
| \displaystyle{ \mp } | U+2213 | Minus-or-Plus sign | Символ минус-плюс | ∓ | ∓ |
- В ISO 8859-1 символ плюс-минус имеет код 0xB1.
- В TeX знаки плюс-минус и минус-плюс кодируются как и соответственно.
- В системе Microsoft Windows для ввода символа плюс-минус можно, прижав клавишу Alt, ввести на цифровой клавиатуре число 0177.
- В системах Linux/Unix сформировать символ плюс-минус можно последовательностью compose +- или одновременным нажатием клавиш ⇧ ShiftAltGr9.
- На компьютерах Макинтош плюс-минус кодируется вводом символов ⌥ Option ⇧ Shift = .
Другое использование
В физике использование знаков плюс и минус для разных электрические заряды был представлен Георг Кристоф Лихтенберг.
В химии надстрочные знаки плюс и минус используются для обозначения иона с положительным или отрицательным зарядом 1 (например, NH+4). Если заряд больше 1, перед знаком пишется число, обозначающее заряд (как в SO2−4). Знак минус также используется вместо в тире, для одинарная ковалентная связь между двумя атомами, как в скелетная формула.[нужна цитата ]
в Международный фонетический алфавит, подписанный знаки плюс и минус используются как диакритические знаки для обозначения выдвинутые или втянутые суставы звуков речи.
Знак минус также используется как тональная буква в орфографии Дэн, Крумен, Караборо, Мван, Ван, Yaouré, Мы, Ньябва и Годье. Символ Unicode, используемый для тональной буквы (U + 02D7), отличается от математического знака минус.
в алгебраическая запись используется для записи игр шахматы, знак плюс + используется для обозначения хода, который ставит оппонента в проверить, а двойной плюс ++ иногда используется для обозначения двойная проверка. Комбинации знаков плюс и минус используются для оценки хода (+/−, + / =, = / +, — / +).
В лингвистике верхний индекс плюс + иногда заменяет звездочка, что означает непроверенный лингвистическая реконструкция.
В ботанические названия, знак плюс означает прививка-химера.
При написании телефонные номера, знак «плюс» обозначает клавиши, необходимые для набора номера из страны, например «00» при звонке из США.
Бонус: примеры программ для тренировки
Для тех, кто хочет улучшить свои навыки в математике, существуют различные программы для тренировки. Они могут быть полезными для детей, студентов и даже преподавателей, которые хотят усовершенствовать свои знания. Вот несколько примеров таких программ:
- Math Workout — приложение, доступное на Android и iOS, которое предлагает тесты по различным математическим темам, таким как арифметика, алгебра и геометрия. Это отличный способ проверить свои знания на практике.
- Khan Academy — это онлайн-платформа с множеством видеоуроков и интерактивных упражнений по математике. Она доступна бесплатно и может быть полезной как для начинающих, так и для опытных учеников.
- Mathematica — это программное обеспечение, которое помогает в решении сложных математических задач. Он может использоваться научными исследователями, инженерами и учеными. Несмотря на то, что это платное ПО, оно предлагает множество функций и возможностей.
Конечно, это лишь небольшой список примеров, и существует множество других программ для тренировки математики. Выбор зависит от ваших целей, уровня знаний и доступности программы. В любом случае, использование этих программ поможет вам улучшить свои математические навыки и стать более уверенным в своих знаниях.
Итоги
Плюс на минус в математике может дать различные результаты в зависимости от контекста. В некоторых случаях, сложение двух чисел с разными знаками дает отрицательный результат, а в других — положительный. Кроме того, плюс на минус может использоваться в других математических операциях, таких как умножение и деление, и также может давать различные результаты в зависимости от контекста.
Однако, на практике, плюс на минус используется для выражения отрицательных чисел. Если некоторое значение или количество должно быть отрицательным, его можно получить путем добавления знака минус (-) перед положительным числом. Таким образом, плюс на минус упрощает работу с отрицательными числами и позволяет избежать ошибок в расчетах.
Более того, понимание, как работает плюс на минус в математике, обеспечивает более глубокое понимание других математических принципов и операций. Знание правил сложения и вычитания, умножения и деления может помочь в решении более сложных математических проблем и задач, как на учебе, так и в жизни.
Таким образом, плюс на минус в математике имеет важное значение для работы с отрицательными числами и является одним из основных принципов математики























