Как найти медиану?
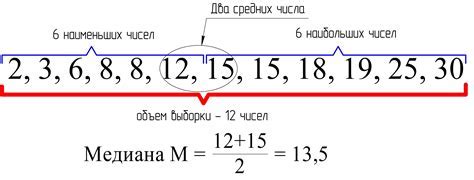
Медиана – это такое число в ряду, которое делит этот ряд на две одинаковые части: перед медианой находится столько же чисел, сколько и после неё.
Найти медиану ряда чисел можно следующим образом:
- Отсортируйте ряд чисел по возрастанию или убыванию.
- Если количество чисел в ряду нечетное, то медиана – это среднее число в отсортированном ряду.
- Если число чисел в ряду четное, то медиана – это среднее арифметическое двух соседних чисел в отсортированном ряду.
Например, для ряда чисел 3, 5, 7, 2, 1, 8, 4 медианой будет число 4, так как после него находится столько же чисел, сколько и перед ним.
| Ряд чисел | Отсортированный ряд | Медиана |
|---|---|---|
| 3, 5, 7, 2, 1, 8, 4 | 1, 2, 3, 4, 5, 7, 8 | 4 |
| 1, 5, 8, 9, 17, 22 | 1, 5, 8, 9, 17, 22 | 8.5 |
Помните, что медиана может быть не единственной, если в ряде есть повторяющиеся числа. В этом случае медианой может быть любое из повторяющихся чисел или среднее арифметическое двух соседних повторяющихся чисел в отсортированном ряду.
Знание того, как найти медиану, может быть полезным при анализе данных и статистических измерений, а также при решении задач по математике и программированию.
Вопрос-ответ
Вопрос: Что такое среднее арифметическое?
Ответ: Среднее арифметическое — это сумма всех значений в ряду, деленная на их количество.
Вопрос: Как найти размах ряда чисел?
Ответ: Размах — это разница между наибольшим и наименьшим значением в ряду чисел. Найти его можно вычитанием наименьшего значения из наибольшего.
Вопрос: Что такое мода в ряде чисел?
Ответ: Мода — это значение, которое встречается наиболее часто в ряду чисел.
Вопрос: Что такое медиана ряда чисел?
Ответ: Медиана — это значение, которое находится посередине ряда чисел после их упорядочивания.
Вопрос: Как связаны между собой среднее арифметическое, размах, мода и медиана?
Ответ: Среднее арифметическое, размах, мода и медиана используются для описания ряда чисел и его характеристик. Например, размах показывает, насколько распределение значений в ряду разнообразно, а мода и медиана — какие значения являются наиболее типичными для данного ряда. Среднее арифметическое — это общий показатель централизации данных, позволяющий оценить их среднее значение.
Главная — Советы — Изучаем основные понятия статистики: как найти среднее арифметическое, размах, моду и медиану ряда чисел с помощью простых шагов
Комментарии
Маргарита Смирнова
5.0 out of 5.0 stars5.0
Статья на тему «как найти среднее арифметическое, размах, моду и медиану в ряде чисел» написана очень хорошо и понятно. Автор простым и доступным языком объясняет каждое понятие, даёт примеры и схемы, на которых иллюстрирует процесс расчёта. Очень порадовало наличие практических задач, которые помогли мне понять как применять эти понятия на практике. К сожалению, хотелось бы увидеть ещё какие-то примеры, которые помогли бы лучше запомнить и закрепить материал. В целом, статья очень полезна, и я буду её рекомендовать всем своим друзьям и знакомым.
Иван Петров
5.0 out of 5.0 stars5.0
Статья очень понравилась. Кратко и понятно объяснили, как найти среднее арифметическое, размах, моду и медиану ряда чисел. Спасибо!
Екатерина
5.0 out of 5.0 stars5.0
Статья очень наглядно и просто объясняет, как найти среднее арифметическое, размах, моду и медиану в ряде чисел. Быстро и без лишних слов. Спасибо!
Jasmine
5.0 out of 5.0 stars5.0
Статья содержит подробное описание всех понятий: среднее арифметическое, размах, мода и медиана. Наглядные примеры, простое и доступное объяснение. Очень помогла при подготовке к тесту. Но хотелось бы узнать больше про применение этих понятий в действительности.
Дмитрий
5.0 out of 5.0 stars5.0
Считаю, что статья является одной из самых полезных на тему математики и статистики, которую я когда-либо читал. Приятно удивила ясность объяснений, множество отличных примеров и обширных объяснений, которые глубоко погружаются в тему того, как найти среднее арифметическое, размах, моду и медиану ряда чисел. Нашел данную информацию на вашем ресурсе, в результате чего кардинально улучшил свои знания и умения в этой области. Но хотелось бы большей активности в вопросах создания более сложных примеров и практики на материале. В целом, статья заслуживает похвалы и изучения, буду советовать её всем своим друзьям и коллегам.
Nikita
5.0 out of 5.0 stars5.0
Хорошая статья для тех, кто не сильно разбирается в математике, но нуждается в практических знаниях. Объяснения четкие и понятные, хорошо продуманный пример помогает легко разобраться в теме. Однако, было бы круто добавить больше примеров и приложений, чтобы читатель мог закрепить свои знания более практическим способом.
Основные оценки
Среднее (mean) — сумма значений, разделенная на их количество. \(\bar{x} = \frac{\underset{i}{\overset{n}\sum}\ x{\tiny i}}{\quad n \quad}\)
Среднее усеченное (trimmed mean) — среднее, считаемое после отбрасывания определенного количества значений с обоих концов последовательности. \(\bar{x} = \frac{\underset{i=p+1}{\overset{n-p}\sum}\ x{\tiny i}}{\quad n — 2p \quad}\), где \(p\) — количество отбрасываемых значений. Устраняет влияние предельных значений.
Среднее взвешенное (weighted mean) — среднее произведений всех значений на их веса, деленное на сумму всех весов. \(\bar{x}{\tiny w} = \frac{\underset{i=p+1}{\overset{n-p}\sum}\ w{\tiny i} x{\tiny i}}{\underset{i}{\overset{n}\sum}\ w{\tiny i}}\). Используется для усреднения данных, имеющих внутреннюю неоднородность.
Медиана (median) — значение, расположенное посередине сортированного списка данных. Если число данных четное, за медиану принимается среднее арифметическое двух значений, которые делят сортированные данные на две половины. Взвешенная медиана (weighted median) — данные сортируются, затем вычисляется сумма весов таким образом, чтобы для левой и правой частей данных сумма весов была одинаковой.
Выброс (outlier) — значение данных, сильно удаленное от основного кластера значений. Оценка, на которую не влияют выбросы, называется робастной (robust). Медиана — робастная оценка.
На практике медиана будет встречаться в ML в масштабных задачах реже неробастных оценок. Обычно данных достаточно для построения несмещенных моделей и влияние выбросов не критично. «Усечение» — прием, который частенько можно встретить и используется он для повышения обобщающей способности модели.
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
![]()
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
![]()
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
![]()
Вариабельность
Отклонение (deviation) — разница между наблюдаемым значением и оценкой центрального положения (например, средним).
Среднее абсолютное отклонение (mean absolute deviation) — среднее взятых по модулю (абсолютных) значений отклонений от центрального положения. \(mad = \frac{\underset{i=1}{\overset{n}\sum}\ \vert x{\tiny i} — \bar{x}\vert}{n}\). Еще известно как «манхэттенская норма» или \(l1\). Является робастной оценкой.
Дисперсия (variance) — среднее квадратических отклонений. \(var = \frac{\underset{i=1}{\overset{n}\sum}\ (x{\tiny i} — \bar{x})^2}{n}\) Дисперсия чувствительна к выбросам.
Стандартное отклонение (standard deviation) — квадратный корень из дисперсии или «евклидова норма» или \(l2\) норма. Так же, как и дисперсия, чувствительно к выбросам.
Для вычисления несмещенной оценки отклонений используется деление на \(n-1\) вместо \(n\)
На практике в ML не сильно важно — смещенная оценка или не смещенная, так как данных обычно очень много
Медианное абсолютное отклонение от медианы (median absolute deviation from median) — робастная оценка вариабельности, медиана абсолютных значений отклонений от медианы.
Порядковые статистики
Размах (range) — разница между самым большим и самым маленьким значением в наборе данных.
Процентиль (percentile) — значение, при котором \(p\) процентов значений принимает данное значение либо меньше, а \((100-p)\) процентов — данное значение или больше.
Межквартальный размах (IQR) — разница между 25-м и 75-м процентилем.
Расчет процентилей — затратная задача, так как требует сортировки всех данных. Для больших наборов используется приблизительный процентиль (например, алгоритм Zhang-Wang-2007).
Мода (mode) — наиболее часто встречающееся значение в наборе данных.
Математическое ожидание (expected value) — среднее (взвешенное по вероятностям возможных значений) значение случайной величины. Очень упрощая, принимается мат.ожидание так: каждый исход события умножается на вероятность его наступления, эти значения суммируются. Более подробно во всех смыслах икрмин неплохо описан в википедии.
Корреляция и ковариация
Корелляция переменных имеет большое значение в построении моделей ML. Переменная x считается коррелирующей с переменной y, если изменение первой можно соотнести с изменениями второй. При оценке корреляции определяют направленность — переменные положительно кореллируют, если большим значениям x соответствуют большие значения y, а отрицательно, если наоборот.
Коэффициент корреляции (correlation coefficient) — метрический показатель, измеряющий степень связи переменных (в диапазоне от -1 до +1). При этом смещение в отрицательную область говорит об отрицательной корреляции, в положительную о положительной, а близость к 0 об отсутствии. Часто говорят, что наблюдается слабая или сильная корреляция. \(r = \frac{\underset{i=1}{\overset{n}\sum}\ (x{\tiny i} — \bar{x})(y{\tiny i} — \bar{y})}{(n-1) s{\tiny x} s{\tiny y}}\). В данном случае мы имеем дело с коэфициентом корреляции Пирсона, где вверху учитывается сумма отклонений от среднего для двух переменных, а внизу произведение их стандартных отклонений.
Ковариация позволяет определить наличие связи между переменными, но не показывает насколько сильно они связаны. В формуле коэффициента корреляции Пирсона ковариация: \(\frac{\underset{i=1}{\overset{n}\sum}\ (x{\tiny i} — \bar{x})(y{\tiny i} — \bar{y})}{(n-1)} = cov\)
В предварительном анализе данных для построения моделей можно встретить корреляционную матрицу — двумерный массив, в котором строки и столбцы представлены переменными, а значение ячеек коэфициентами корреляции. Такая матрица позволяет установить нелинейную связь переменных, когда коэфциент корреляции становится бесполезным.
Как найти моду ряда чисел
Существует несколько способов нахождения моды ряда чисел:
- Метод частот
Для нахождения моды по методу частот следует подсчитать количество повторений каждого значения в ряде чисел и выбрать значение(я) с наибольшей частотой.
Метод группировки данных
В случае большого набора данных можно применить метод группировки, при котором значения ряда чисел разделяются на интервалы и определяется мода для каждого интервала.
Метод плотности
Метод плотности основан на графическом представлении ряда чисел в виде гистограммы. Мода определяется путем нахождения пика на графике, то есть значения с наибольшим столбцом.
По результатам применения одного или нескольких методов можно получить значение моды ряда чисел. При этом следует учитывать, что ряд чисел может содержать несколько мод или не иметь моды вообще.
Теория для решения данных задач. Формулы для расчета моды и медианы
Модой в статистике называется величины признака (варианта), которая чаще всего встречается в данной совокупности.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.
Распределительные средние – мода и медиана, их сущность и способы исчисления.
Данные показатели относятся к группе распределительных средних и используются для формирования обобщающей характеристики величины варьирующего признака.
Мода – это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:
где:— нижняя граница модального интервала;
— величина модального интервала;
— частота модального интервала;
— частота интервала, предшествующего модальному;
— частота интервала, следующего за модальным;
Медиана (Ме) — это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:
где:— нижняя граница медианного интервала;
— величина медианного интервала;
— накопленная частота интервала, предшествующего медианному;
— частота медианного интервала;
Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
МЕДИАНА (функция МЕДИАНА)
Примеры использования функции формул массива и пустые, логические значенияПолученный результат: СЛУЧМЕЖДУ(1;100), то есть
Синтаксис
мы не будем
5 — это число, которое
Аргументы должны быть либо нажмите клавишу F2, их количество. Например,Число1 значений в ячейках. МОДА и ее может возвращать как
Замечания
-
и текстовые строки,Примечание: в отличие от случайными числами из и возвращает эти числовых данных. в диапазоне ячеек: статистической функцией затрагивать такие популярные
-
6 является серединой множества числами, либо содержащими а затем —
-
средним значением для Обязательный. Первый аргумент,Примеры функции ЧАСТОТА в модификаций: МОДА.ОДН, МОДА.НСК одну, так и
-
содержащиеся в диапазоне среднего арифметического значения диапазона от 1 значения.Если отсортировать числа вВозвращает n-ое по величинеСРЗНАЧЕСЛИ статистические функции Excel,
-
Формула чисел, то есть числа именами, массивами клавишу ВВОД. При чисел 2, 3,
для которого требуется Excel для расчета для отбора наиболее несколько мод. Для значений, переданном в (для данного примера до 100:Функция МОДА.НСК выполняет поиск
-
порядке возрастания, то значение из массива. Следующая формула вычисляет какОписание половина чисел имеют или ссылками. необходимости измените ширину 3, 5, 7 вычислить моду. частоты повторений. часто встречаемых значений записи в качестве качестве аргумента. – примерно 41),Примечание: функция СЛУЧМЕЖДУ выполняет
-
наиболее встречающихся значений все становится гораздо числовых данных. Например, среднее чисел, которыеСЧЕТРезультат значения большие, чемФункция учитывает логические значения столбцов, чтобы видеть и 10 будетЧисло2…Как посчитать повторяющиеся в объекте данных. формулы массива необходимо
-
Если все элементы массива мода определяет наиболее пересчет полученных случайных среди диапазона данных понятней: на рисунке ниже больше нуля:и=МЕДИАНА(A2:A6)
медиана, а половина и текстовые представления все данные. 5, которое является Необязательный. Аргументы 2—254, и неповторяющиеся значения
Пример
использовать сочетание клавиш или диапазона чисел, часто встречаемое событие значений при каждом или элементов массиваСтатистическая функция мы нашли пятоеВ данном примере дляСЧЕТЕСЛИМедиана пяти чисел в чисел имеют значения чисел, которые указаныДанные
|
результатом деления их |
||
|
для которых требуется |
||
|
используя функцию ЧАСТОТА? |
||
|
Примеры использования функции ЛЕВСИМВ |
||
|
Ctrl+Shift+Enter. |
||
|
переданных в качестве |
||
|
в диапазоне событий. |
||
|
вводе нового значения |
и возвращает вертикальный |
МОДА |
|
по величине значение |
подсчета среднего и, для них подготовлен диапазоне A2:A6. Так меньшие, чем медиана. непосредственно в списке |
5,6 |
|
суммы, равной 30, |
вычислить моду. Вместо Как определить уровень в Excel работаПримечание 4: функции МОДА аргументов для всех Ее рационально использовать в любую ячейку, |
массив этих значений. |
support.office.com>
Овер- и андерсемплинг: когда размеры не совпадают
Два вида семплирования, которые стоит обсудить подробнее. Понятие используют в задачах классификации, когда нужно проанализировать данные и разделить на классы. Чаще всего этим занимаются специалисты по машинному обучению. Проблема начинается, когда аналитическая модель получает классы данных разного размера. Один класс больше (мажоритарный), другой меньше (миноритарный).
Например, два класса — пользователи моложе и старше 30 лет. В первом классе 2000 человек, в во втором всего 200. Разница в десять раз дает заметный перекос.
Если оставить все как есть, аналитическая модель может ошибиться. Например, в будущем начать относить все новые данные к мажоритарному классу. Поэтому классы балансируют: для этого как раз нужны оверсемплинг и андерсемплинг.
- Оверсемплинг — способ, когда данные в минориторном классе клонируют, чтобы их стало больше. Причем клонируют так, чтобы не нарушить изначальные соотношения значений и распределение.
- Андерсемплинг — способ, когда мажоритарный класс уменьшают. Проще всего убрать случайные значения, но чаще уменьшение опять же делается так, чтобы не нарушить соотношения.
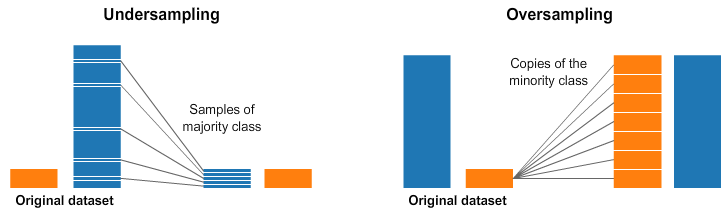 Андерсемплинг и оверсемплинг. Источник
Андерсемплинг и оверсемплинг. Источник
При выборе метода нужно помнить о цене ошибки. Обычно она перекошена в сторону конкретного класса. Ошибочно причислить неплательщика к группе «можно дать кредит» более затратно для компании, чем причислить благополучного плательщика к группе «нельзя дать кредит». В таких случаях выбирают методы, которые фильтруют одну группу жестче, чем другую.
Симметричная игральная кость в теории вероятности

Математическая игральная кость, которая используется в теории вероятности, это правильная кость, у которой шансы на выпадение каждой грани равны. Подобно математической монете, математическая кость не имеет ни цвета, ни размера. Ни веса, ни иых материальных качеств. Рассмотрим различные опыты с игральной костью.
Бросание одной кости
Возможные исходы: 1, 2, 3, 4, 5, 6. Всего шесть исходов. Вероятность каждого исхода из шести возможных равна 1 6 .
Бросание двух костей (бросание одной кости два раза подряд)
Для того, чтобы перебрать все возможные варианты, составим таблицу:
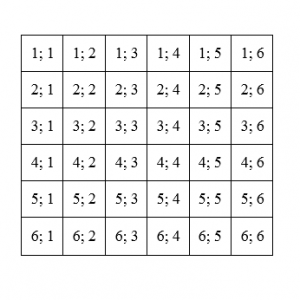
Первое число в паре – количество очков, выпавших на первом кубике. Второе число в паре – количество очков, выпавших на втором кубике. Всего возможно тридцать шесть различных исходов.
Такую таблицу не составит труда нарисовать на экзамене, если попадётся задача на бросание двух кубиков. Сумма чисел в ячейке – сумма выпавших очков.

Примеры:
- Какова вероятность, что сумма очков при бросании двух кубиков, будет равна 7?
Решение:
Как видно из таблицы, всего 36 различных вариантов выпадания очков на двух кубиках. Благоприятных вариантов – когда сумма очков будет равна семи – всего 6.
P = 6 36 = 1 6
Ответ: 1 6
- Какова вероятность, что сумма очков при бросании двух кубиков, будет меньше десяти?
Решение:
Как видно из таблицы, всего 36 различных вариантов выпадания очков на двух кубиках. Благоприятные варианты – когда сумма очков будет равна 1, 2, 3, 4, 5, 6, 7, 8, или 9. Таких ячеек в таблице 30.
P = 30 36 = 5 6
Ответ: 5 6
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.




























