Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют
Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется
Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна
А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Как вычислить ускорение?
Ускорение определяется как отношение изменения скорости к затраченному времени. Если скорость объекта меняется от начального значения U до конечного значения V за время t, то ускорение a можно вычислить по формуле: a = (V — U)/t.
Рассмотрим пример, где объект изначально покоится и достигает скорости 10 м/с через пять секунд. Каково будет ускорение в этом случае?
Исходная скорость U равна 0 м/с, так как объект находится в покое. Конечная скорость V равна 10 м/с. Время t равно 5 секундам. Следовательно, ускорение a будет равно (10 м/с — 0 м/с) / 5 сек = 2 м/с².
Единицы измерения ускорения: м/с² (метры в секунду в квадрате)
Преимущества ускорения:
- Позволяет измерить изменение скорости
- Объясняет поведение тел при разгоне или торможении
- Используется для расчета времени, за которое объект достигнет заданной скорости
Недостатки ускорения:
- Необходимость учета изменения направления движения
- Не может быть измерено напрямую, требует расчетов
Рубрики новостей
- 16K
- 1D X
- 3D
- 4К
- 5D mark 2
- 5D mark III
- 8K
- A6700
- Adobe Premiere Pro
- After Effects
- Apple
- Aputure
- Blackmagic
- Canon
- Canon 90D
- Canon EOS M
- Canon M6 Mk. II
- Disney
- DIY
- DJI
- DJI OSMO Mobile 3
- EOS R
- EOS-1D C
- FAA
- follow focus
- Fujifilm
- GoPro
- Gudsen Moza
- HERO 8
- Insta360
- KineRAW
- making of
- Moment
- NAB
- Nicon Z8
- Nikon
- Nikon D6
- NVIDIA
- Panasonic
- RED
- Samsung
- Screen X
- Sharp
- Sigma
- SONY
- Sony
- Sony A7R IV
- Teradek
- Varavon
- VooDoo
- VR
- Zhiyun-Tech
- Анимация
- Аудио
- Биография
- Вертолеты
- Видео
- Видеоредактор
- Видеоэффекты
- Видоискатель
- Грим
- Дроны
- Дымка
- Звук
- Кино
- Кинокамера
- Кинооператоры
- Композитинг
- Кран
- Мониторы
- Монтаж
- Новости
- Новый год
- Обвес
- Оборудование
- Объективы
- Подводная съемка
- Приемы в кино
- Программное обеспечение
- Ремейк
- Рождество
- Свет
- Светофильтры
- Слайдер
- Смартфоны
- События
- Софт
- Спецэффекты
- Стабилизаторы
- Стабилизация изображения
- Старое кино
- Стедикам
- Сценарий
- Съемка автомобилей
- Т34
- Телефоны
- Трюки
- Уроки
- Фото
- Фотокамеры
- Художник по гриму
- Цветовая коррекция
- Штативы
- Экшн камеры
- Эффекты
- Юмор
Ускорение и его составляющие
В
случае неравномерного движения важно
знать, как быстро изменяется скорость
с течением времени. Физической величиной,
характеризующей быстроту изменения
скорости по модулю и направлению,
является ускорение. Рассмотримплоское
движение, т.
е
такое, при котором все участки
траектории точки лежат в одной плоскости.
Пусть вектор v
задает
скорость точки
Рассмотримплоское
движение, т.
е. такое, при котором все участки
траектории точки лежат в одной плоскости.
Пусть вектор v
задает
скорость точки
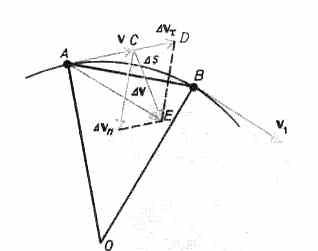
А в
момент времени t.За
время tдвижущаяся
точка перешла в положение Ви
приобрела скорость, отличную от v
как
по модулю, так и направлению и равную
v1=v
+ v.
Перенесем
вектор v1
в
точку Аи
найдем v
(рис.4).
Средним
ускорением неравномерного
движения в интервале от t
до t+tназывается
векторная величина, равная отношению
изменения скорости v
к
интервалу времени t:
Мгновенным
ускорением а (ускорением)
материальной точки в момент времени tбудет
предел среднего ускорения:
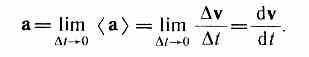
Таким образом,
ускорение а есть векторная величина,
равная первой производной скорости по
времени.
Разложим
вектор v
на
две составляющие. Для этого из точки А(рис.
4) по направлению скорости v
отложим
вектор
AD,по
модулю равный v1.
Очевидно,
что вектор CD,равный
v,
определяет
изменение скорости по
модулю за
время t:
v=v1—v.Вторая
же составляющая вектора v-vn
характеризует
изменение скорости за время tпо
направлению.
Тангенциальная
составляющая ускорения
11
т.е.
равна первой производной по времени от
модуля скорости, определяя тем самым
быстроту изменения скорости по модулю.
Найдем вторую составляющую ускорения.
Допустим, что точка Вдостаточно
близка к точке А,поэтому
As
можно
считать дугой окружности некоторого
радиуса r,
мало отличающейся от хорды АВ.Тогда
из подобия треугольников АОВиEADследует
vn/AB
= v1/r,но
так как AB
= vt,то
В
пределе при t0
получим v1v.
Поскольку
v1v,
уголEADстремится
к нулю, а так как треугольник EADравнобедренный,
то угол ADEмежду
v
и
vnстремится
к прямому. Следовательно, при t0
векторы vn
и
v
оказываются
взаимно перпендикулярными. Так как
вектор скорости направлен по касательной
к траектории, то вектор vn,
перпендикулярный
вектору скорости, направлен к центру
ее кривизны. Вторая составляющая
ускорения, равная
называетсянормальной
составляющей ускорения и
направлена по нормали к траектории к
центру ее кривизны (поэтому ее называют
также центростремительным
ускорением).
Полное
ускорение тела
есть геометрическая сумма тангенциальной
и нормальной составляющих (рис.5):
Итак,тангенциальнаясоставляющая
ускорения характеризует быстроту
изменения скорости по модулю (направлена
по касательной к траектории), а нормальнаясоставляющая
ускорения — быстроту изменения скорости
по направлению (направлена к центру
кривизны траектории).
В зависимости от
тангенциальной и нормальной составляющих
ускорения движение можно классифицировать
следующим образом:
1) а=0,
аn
= 0 — прямолинейное равномерное движение;
2)
a=a=const,
an=0
—
прямолинейное равнопеременное движение.
При таком виде движения
Если
начальный момент времени t1=0,а
начальная скорость v1=v,то,
обозначив t2
= t иv2
= v, получим
a
= (v-v)/t,откуда
v
=v+at.
Проинтегрировав
эту формулу в пределах от нуля до
произвольного момента времени t,найдем,
что длина пути, пройденного точкой, в
случае равнопеременного движения
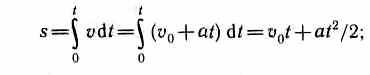
3)
а=f(t),
аn=0
— прямолинейное движение с переменным
ускорением;
4) а=0,
аn=const.
При
а=0
скорость по модулю не изменяется, а
изменяется по направлению. Из формулы
аn=
v2/r
следует, что радиус кривизны должен
быть постоянным. Следовательно, движение
по окружности является равномерным;
5) а=0,
аn0
— равномерное криволинейное движение;
6)
a=const,
an0—криволинейное
равнопеременное движение;
7)a=
f(t), an0
—
криволинейное движение с переменным
ускорением.
12
Основная задача механики
Это строки из замечательного произведения Марка Твена «Приключения Тома Сойера»
Том целый день копался в земле то у дерева, то на холме, но клада так и не нашел. Прежде, чем отправиться за кладом, надо знать, где он находится.
Умение найти положение любого тела в данный момент времени и есть основная задача механики. Эту задачу решают диспетчеры, отправляющие поезд в путь. Они должны знать, как двигаются поезда, иначе – авария. Отправляя самолет в рейс, ракету в полет, специальные службы просчитывают траектории их движения. Космический корабль в огромных просторах космоса должен встретиться и состыковаться со станцией. Для этого надо произвести точнейшие расчеты, чтобы избежать ошибок, приводящих к неудаче.
Почему Том Сойер не мог решить основную задачу механики? Чтобы определить положение тела, надо знать еще какое-то тело, от которого вести отсчет расстояния, и направление, куда это расстояние отмерять. Герои «Острова сокровищ» (автор книги Роберт Стивенсон) смогли найти место, где лежал клад, так как у них была информация о направлении поиска и о дереве, от которого надо вести отсчет расстояния.
Так было написано на карте, которая вела к кладу на острове Сокровищ.
Стоит разобраться в записке на карте. Итак, высокое дерево – это тело, от которого надо вести отсчет расстояния в указанном направлении. Дано и расстояние — «в десяти саженях». Основная задача механики здесь решается.
Чтобы определить, где находится тело на прямой, на плоскости, в пространстве, нужно знать:
Если соединить по прямой тело отсчета с местом, где оказалось движущееся тело, получится отрезок, имеющий длину и направление (в сторону от тела отсчета до нового положения). Этот отрезок называется перемещением. Для обозначения используется буква s, но в отличие от пройденного пути над буквой ставится стрелка, так как перемещение есть векторная величина. Пройденный путь – это скаляр, он имеет только длину.
Итак, перемещение — это вектор, соединяющий начальное и конечное положение тела.
(Источник)
Имея тело отсчета и перемещение, легко можно справиться с основной задачей механики.
При движении тела по прямой численные значения перемещения и пройденного пути совпадают и находятся по формуле s = v ∙ t. А если движение криволинейно? Вот три различных примера.
- На соревнованиях по ориентированию, двигаясь от старта строго по компасу на северо-восток, Миша прошел 670 м. В этом случае 670м – это и пройденный мальчиком путь, и модуль вектора перемещения, направление которого задано.
- Дима с Сережей отправились в лес за грибами. В лес они зашли от столба с пометкой 5 км. Набрав по корзинке грибов, друзья через 2 ч вышли на шоссе у столба с пометкой 6 км. Разве ребята прошагали по лесу 1 км? В этом случае перемещение мальчиков направлено от первого столба ко второму и по модулю равно 1 км. А вот пройденный путь, который прошли мальчики за 2 ч, двигаясь по сложной траектории, составляет несколько километров.
- Братья Чук и Гек после прогулки вернулись домой. Начало совпадает с концом пути. Перемещение братьев получается равным нулю. За время прогулки дети прошли несколько метров, значит пройденный путь, в отличие от перемещения, нулю не равен.
Итак:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законамМасса — это мера инертности телаСила — это количественная мера взаимодействия тел.
Второй закон Ньютона:Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F{→} = m⋅a{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона: Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1{→} = -F_2{→} $
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.
Закон Гука записывают в виде
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значенияГравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:Весом телаСила тяжестиНевесомостьюИскусственный спутник ЗемлиПервая космическая скорость
1.3. Основные понятия и законы статики и гидростатики
устойчивое, неустойчивое и безразличное.устойчивое равновесие.неустойчивое положениебезразличноеПлечом силыУсловие равновесия рычага:Давлениемзакон Паскаля:Гидравлический прессA1 = A2.силой Архимедазакон АрхимедажидкпогрУсловие плавания тела
1.4. Законы сохранения
Импульсом телаимпульсом силы.закон сохранения импульсаМеханической работойМощностьэнергией.кинетическую и потенциальную.кинетической энергией.потенциальной энергией.Энергия сжатой пружины:механическую энергию.закон сохранения механической энергии
1.5. Механические колебания и волны
КолебаниямиГармоническими колебаниямиамплитудой колебанийПериодом TЧастотой периодических колебаний-1Математическим маятникомПериод колебаний математического маятникаПериод колебаний груза на пружинеРаспространение колебаний в упругих средах.поперечнойпродольнойДлиной волныЗвуковыми волнами
Ускорение при равноускоренном прямолинейном движении
Ускорение тела равно отношению изменения вектора скорости к времени, в течение которого происходит это изменение.
v — скорость тела в этот момент времени. v — это скорость объекта в начальный момент времени, а t — время, в течение которого скорость изменилась.
Пример 1. Поезд движется и достигает скорости 36 км/ч за 20 секунд. Найдите ускорение этого ускорения.
Во-первых, договоритесь о единицах измерения. Для этого переведем скорость в м/с. Умножьте километры на 1000 и разделите на 3600 (в часе содержится большое количество секунд). Результат — 10 м/с.
Начальная скорость поезда равна 0 м/с, так как изначально поезд был неподвижен. Получив все данные, вы можете подставить их в формулу, чтобы найти ускорение
Проекция ускорения
vвату проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, а t — время, в течение которого скорость изменилась.
Знак проекции ускорения зависит от направления, в котором вектор ускорения направлен относительно оси OX.
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задачи равномерно ускоряющегося линейного движения проекция величины может быть записана без нижнего указателя, так как при движении объекта по прямой его положение изменяется относительно единственной оси (OX). Если движение описывается более чем одной осью, они должны быть записаны.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости.
Равномерно замедляющееся движение — это частный случай равномерно ускоряющегося движения, при котором скорость за один и тот же промежуток времени уменьшается на одну и ту же величину. Направления векторов скорости и ускорения противоположны друг другу (a. ↓v).
Пример 2. Автомобиль сначала разгоняется, а затем замедляется. Во время ускорения скорость и скорость вектора ускорения совпадают, так как скорость увеличивается. Однако при торможении скорость уменьшается, поскольку направление вектора ускорения меняется на противоположное.
Направление тангенциального ускорения
Направление тангенциального ускорения зависит от типа движения объекта по траектории. Рассмотрим несколько случаев:
- Если объект движется по прямой, то направление тангенциального ускорения совпадает с направлением движения.
- Если объект движется по окружности с постоянной скоростью, то направление тангенциального ускорения направлено по касательной к окружности.
- Если объект движется по окружности с переменной скоростью, то направление тангенциального ускорения всегда направлено по касательной к траектории. При этом, если скорость увеличивается, тангенциальное ускорение направлено в том же направлении, что и скорость. Если скорость уменьшается, направление тангенциального ускорения противоположно направлению скорости.
Направление тангенциального ускорения играет важную роль при решении физических задач, связанных с изучением движения тел. Понимая направление тангенциального ускорения, можно определить, как меняется скорость объекта и предсказать дальнейшее движение.
Векторное представление тангенциального ускорения
Векторное представление тангенциального ускорения характеризуется как модулем, так и направлением. Модуль ускорения определяется как изменение скорости объекта за единицу времени. Направление тангенциального ускорения всегда сонаправлено с вектором скорости.
Для математической записи векторного представления тангенциального ускорения используется символ at. Здесь «t» означает тангенциальное (касательное) направление. Вектор аt может быть представлен как:
at = v2 / R
где v — скорость объекта, а R — радиус кривизны его траектории.
Векторное представление тангенциального ускорения является важным понятием в динамике и механике. Оно позволяет определить, как изменяется движение объекта при изменении его скорости и направления.
Таким образом, векторное представление тангенциального ускорения важно для изучения механики и движения тел в пространстве
Направление вращательного движения
Когда рассматриваем вращательное движение, необходимо учитывать направление углового ускорения, а не просто его величину. В уравнении движения твердого тела можно выделить две главные компоненты вращательного движения: угловое ускорение и момент силы, действующий на тело.
Направление вращательного движения определяется согласно правилу правой руки. Если положить правую руку так, чтобы пальцы указывали в направлении вектора угловой скорости, то большой палец будет указывать направление вектора углового ускорения. Таким образом, вектор углового ускорения ортогонален плоскости вращательного движения и определяет направление изменения угловой скорости.
Определение направления вращательного движения важно для решения разнообразных задач, связанных с динамикой вращательного движения. Например, для определения направления силы, необходимой для изменения угловой скорости твердого тела, или для понимания эффектов прецессии и нутации. Ориентация тела в пространстве определяется вектором угловой скорости, а его изменение — вектором углового ускорения
Знание направления вращательного движения позволяет более точно моделировать, предсказывать и анализировать поведение твердых тел, и использовать их в различных сферах науки и техники
Ориентация тела в пространстве определяется вектором угловой скорости, а его изменение — вектором углового ускорения. Знание направления вращательного движения позволяет более точно моделировать, предсказывать и анализировать поведение твердых тел, и использовать их в различных сферах науки и техники.
| Вектор угловой скорости | Вектор углового ускорения |
|---|---|
| Ортогонален плоскости вращательного движения | Определяет направление изменения угловой скорости |
| Определяет ориентацию тела в пространстве | Позволяет более точно моделировать и анализировать поведение твердых тел |
Подробнее о скорости: что же это такое
Достаточно просто, не так ли? Точнее говоря (физики очень любят точность), скорость равняется изменению положения, деленному на изменение времени. Потому скорость движения вдоль оси X можно выразить следующим образом:
В реальном мире скорость может принимать очень разные формы, некоторые из них описываются в следующих разделах.
Смотрим на спидометр: мгновенная скорость
Итак, у нас уже есть общее представление о скорости. Именно ее измеряет спидометр автомобиля, не так ли? Когда вы катите по прямолинейному шоссе, все, что нужно делать, — всего лишь следить за показаниями спидометра. “Уже 140 километров в час. Пожалуй, сбросим скорость до 120”. Именно так мы часто поступаем в жизни, а иначе говоря, так мы определяем мгновенную скорость.
Движемся постоянно: равномерная скорость
А что если долгое время автомобиль едет со скоростью 120 километров в час? В физике эта скорость называется равномерной (или постоянной), а в жизни она возможна только при движении на абсолютно ровных и прямолинейных дорогах, когда долгое время можно поддерживать движение без изменения скорости.
Равномерное движение с постоянной скоростью является простейшим видом движения, поскольку оно никак не меняется.
Движемся вперед и назад: неравномерное движение
Название этого типа движения говорит само за себя: неравномерное движение означает движение со скоростью, меняющейся со временем. Именно с такой скоростью мы чаще всего сталкиваемся в повседневной жизни. Вот как выглядит уравнение изменения скорости от исходной скорости \( v_1 \) до конечной скорости \( v_0 \):
Остальная часть этой главы посвящена ускорению, которое характеризует неравномерность движения.
Жмем на секундомер и определяем среднюю скорость
Выражение со скоростями не так уж неосязаемо, как может показаться. Измерения скорости можно сделать более конкретными. Допустим, что вам хочется совершить путешествие из Нью-Йорка в Лос-Анджелес, которые находятся на расстоянии около 2781 миль друг от друга. Если предположить, на это путешествие ушло 4 суток, то какой была ваша скорость?
Скорость можно найти, если поделить пройденное расстояние на затраченное на это время:
Итак, результат 695,3 получен, но в каких единицах он выражен?
В этом выражении мили делятся на сутки, т.е. результат равен 695,3 милям в сутки. Это не совсем стандартная единица измерений и вполне естественно было бы поинтересоваться: а сколько это миль в час? Для ответа на этот вопрос нужно перевести сутки в часы, как показано в главе 2. Поскольку в сутках 24 часа, то получим следующий результат:
Итак, получен более понятный результат 28,97 миль в час. Смущает лишь столь малая величина скорости, ведь обычно машины едут со скоростью в 2-3 раза быстрее, однако среднюю скорость для всего путешествия мы вычислили, разделив все расстояния на все время, включая время отдыха.
Средняя скорость и неравномерное движение
Средняя скорость отличается от мгновенной, если только вы не движетесь равномерно, когда скорость вообще не меняется. А средняя скорость неравномерного движения, когда все расстояние делится на все время, может отличаться от мгновенной скорости.
Путешествуя из Нью-Йорка в Лос-Анджелес, вам наверняка придется провести несколько ночей в отелях, и во время вашего отдыха мгновенная скорость автомобиля равна 0 миль в час, а средняя скорость — 28,97 миль в час! Дело в том, что средняя скорость получена в результате деления всего расстояния на все время.
Средняя скорость может зависеть от фактически пройденного пути. Допустим, что, путешествуя по штату Огайо, вы решили подвезти попутчика в штат Индиана и погостить у вашей сестры в штате Мичиган. Все путешествие может иметь вид, показанный на рис. 3.3: первые 80 миль — в штат Индиана, а потом 30 миль — в штат Мичиган.
Если ехать со скоростью 55 миль в час, то для преодоления всего пути длиной 80 + 30 = 110 миль потребуется 2 часа. Но если взять расстояние по прямой между начальной и конечной точкой путешествия, которое равно 85,4 миль, то средняя скорость будет равна:
Таким образом, получена средняя скорость для расстояния от начальной до конечной точки путешествия вдоль пунктирной линии. Но если вам нужно определить скорость для каждого из двух отрезков фактически пройденного пути, то нужно измерить длину каждого из двух отрезков и разделить их на время их прохождения.
При движении с равномерной скоростью это можно сделать легко и просто, поскольку в таком случае средняя скорость равняется мгновенной скорости в любой точке пути.



























