Перемешанные карты в колоде
Перемешанные карты в колоде — это способ случайного распределения карт при игре в карточные игры, чтобы исключить возможность предсказания следующей карты и сохранить игровую ситуацию в неизвестности.
Примеры карт, которые могут быть перемешаны в колоде:
- Пиковый туз
- Червонная десятка
- Крести двойка
- Бубновая пятерка
- Трефовая королева
Распределение карт в колоде может происходить различными способами:
- Альтернативное расположение карт — карты разных мастей перемешиваются друг с другом, чтобы распределение карт в колоде было более случайным.
- Проверка на сопоставление — после перемешивания колоды производится проверка на подозрительные сопоставления карт, чтобы исключить возможность мошенничества.
- Математический алгоритм — существуют различные математические алгоритмы перемешивания карт, которые гарантируют случайное распределение карт в колоде.
Перемешанные карты в колоде обеспечивают справедливость игры и добавляют элемент случайности, делая игру более интересной и непредсказуемой для всех участников.
Итераторы
Итератор — это объект, указывающий на некоторый элемент цепочки элементов, позволяющий перебирать элементы цепочки с помощью некоторого набора операций. Процесс перебора элементов цепочки называется итерированием.
Наиболее очевидный пример итератора — это указатель: указывает на объект, позволяет итерировать массив через инкремент и декремент. В C++ синтаксис итераторов заимствован у указателей.
Классификация
Выделяют пять типов итераторов. Ниже представлены итераторы в порядке убывания их силы.
- Random Access. Это наиболее мощный тип итераторов. Random access поддерживает произвольный доступ к последовательности элементов. По сути равносилен указателем: поддерживает операции инкремента(++), декремента (--), прибавления целого числа (+ val, - val), разыменования (*), разыменования со сдвигом ([]), доступа к члену (->). Как пример, итераторы такого типа предоставляет vector.
- Bidirectional. Двунаправленный итератор является более слабым типом итераторов: позволяет двигаться только вперед и назад, проходя через каждый элемент. Операции: ++, --, *, ->. Как пример, итераторы такого типа предоставляет list.
- Forward. Однонаправленный итератор позволяет двигаться только в одном направлении. Операции: ++, *, ->
- Input. Однонаправленный итератор, позволяющий только считывать данные, но не записывать.
- Output. Однонаправленный итератор, позволяющий только записывать данные, но не считывать.
Вне данной классификации лежит Reverse iterator. Reverse iterator обращает направление для bidirectional и random access итераторов. Для получения начала и конца итератора необходимо вызвать rbegin() и rend() соответственно.
Reverse iterator реализует функцию base(), возвращающую обычный итератор. Для того, чтобы получить из обычного (bidirectional и random access) итератора reverse, достаточно использовать оператор присваивания.
set< int > s; set< int > :: reverse_iterator i = s.rbegin(); set< int > :: iterator j = i.base(); i = j
Внимание, вопрос. Почему в одну сторону можно написать i = j, а в другую только j = i.base()?Внимание, вопрос
Почему нельзя менять значения в set?
Служебная информация
Для описания итератора в С++ существует шаблон iterator_traits. Стандартные алгоритмы получают необходимую информацию об итераторах из специализаций этого шаблона для конкретного итератора.
Определение iterator_traits выглядит следующим образом.
template <class Iterator> struct iterator_traits {
typedef typename Iterator::difference_type difference_type;
typedef typename Iterator::value_type value_type;
typedef typename Iterator::pointer pointer;
typedef typename Iterator::reference reference;
typedef typename Iterator::iterator_category iterator_category;
}
- difference_type описывает тип разности итераторов.
- value_type — тип объекта, на который указывает итератор.
- pointer — тип указателя на объект
- reference — тип ссылки
- iterator_category_tag — категория итератора. Может быть
- input_iterator_tag
- output_iterator_tag
- forward_iterator_tag
- bidirectional_iterator_tag
- random_access_iterator_tag
Стандартные функции
advance(iterator, n) — сдвигает итератор на n элементов. Для random access и bidirectional значение n может быть отрицательным. Работает со всеми типами итераторов вплоть до input. Для random access сдвигается сразу на n элементов, для остальных — использует инкремент (или декремент).
distance(iterator first, iterator last) находит число элементов между first и last. Для radnom access использует значение разности итераторов, для остальных — использует линейный поиск.
Последовательности чисел
Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.
Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.
Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.
Что такое числовая последовательность?
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
- для каждого натурального числа существует элемент данного множества;
- это число является номером элемента и обозначает позицию данного элемента в последовательности;
- для любого элемента последовательности можно указать следующий за ним элемент.
Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.
Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.
На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.
Ограниченные и неограниченные последовательности
Определение 4.
Числовую последовательность
x
1 , x
2 , … x n
, …
называют ограниченной сверху,
если существует такое число M,
что каждый член этой последовательности меньше
числа M
.
Другими словами, для всех n
= 1, 2, 3, …
выполнено неравенство
Определение 5.
Числовую последовательность
x
1 , x
2 , … x n
, …
называют ограниченной снизу,
если существует такое число m,
что каждый член этой последовательности больше
числа m
.
Другими словами, для всех n
= 1, 2, 3, …
выполнено неравенство
Определение 6.
Числовую последовательность
x
1 , x
2 , … x n
, …
называют ограниченной,
если она ограничена и сверху, и снизу.
Другими словами, существуют такие числа M
и m,
что для всех n
= 1, 2, 3, …
выполнено неравенство
m
Определение 7.
Числовые последовательности, которые не являются ограниченными
, называют неограниченными последовательностями
.
Пример 6
. Числовая последовательность
1, 4, 9, … n
2 , …
заданная формулой
x n
= n
2 , n
= 1, 2, 3, … ,
ограничена снизу
, например, числом 0.
Однако эта последовательность неограничена сверху
.
Пример 7
. Последовательность
Пусть
X
{\displaystyle X}
— это либо множество вещественных чисел
R
{\displaystyle \mathbb {R} }
, либо множество комплексных чисел
C
{\displaystyle \mathbb {C} }
. Тогда последовательность
{
x
n
}
n
=
1
∞
{\displaystyle \{x_{n}\}_{n=1}^{\infty }}
элементов множества
X
{\displaystyle X}
называется числовой последовательностью
.
Свойства
Повторяемость и уникальность
Упорядоченная последовательность характеризуется повторяемостью, то есть элементы могут повторяться в последовательности. Однако каждый элемент в упорядоченной последовательности является уникальным и занимает определенное место в последовательности.
Изменяемость и неизменяемость
Упорядоченная последовательность может быть изменяемой или неизменяемой. Если последовательность изменяемая, то элементы в ней могут быть добавлены, удалены или изменены в любой момент времени. Если последовательность неизменяемая, то элементы в ней нельзя изменить после создания.
Индексация
Упорядоченная последовательность имеет индексацию, то есть каждый элемент имеет свой номер или индекс в последовательности. Нумерация индексов начинается с нуля для первого элемента и увеличивается на единицу для каждого последующего элемента.
Сортировка
Упорядоченная последовательность может быть отсортирована по определенным критериям. Например, элементы могут быть отсортированы по возрастанию или убыванию, а также по алфавитному или числовому порядку.
Итерируемость
Упорядоченная последовательность является итерируемой, то есть ее элементы можно перебрать в цикле или с помощью итератора. Это позволяет выполнять различные операции с каждым элементом последовательности.
Объединение и разделение
Упорядоченные последовательности могут быть объединены в одну последовательность, а также разделены на более мелкие последовательности по определенным критериям. Например, можно объединить несколько списков в один список или разделить список на подсписки по определенному значению.
Теоремы
Теоремы о пределах последовательностей — важная составляющая теории, без которой невозможна практика. Есть всего лишь четыре главных теоремы, запомнив которые, можно в разы облегчить ход решения или доказательства:
- Единственность предела последовательности. Предел у любой последовательности может быть только один или не быть вовсе. Тот же пример с очередью, у которой может быть только один конец.
- Если ряд чисел имеет предел, то последовательность этих чисел ограничена.
- Предел суммы (разности, произведения) последовательностей равен сумме (разности, произведению) их пределов.
- Предел частного от деления двух последовательностей равен частному пределов тогда и только тогда, когда знаменатель не обращается в ноль.
Значение рандомизации в исследованиях и практике
Рандомизация, или случайное размещение участников или элементов исследования в разные группы или условия, является важным аспектом в многих исследованиях и практике. Она позволяет ученым получать более достоверные результаты и уменьшает возможное влияние внешних факторов.
Зачем нужна рандомизация?
Использование случайной рандомизации позволяет создать условия, при которых участники и элементы исследования распределяются на группы или условия исследования таким образом, чтобы в каждой группе было примерно равное количество участников или элементов. Это позволяет исключить возможное систематическое смещение и обеспечивает сопоставимость групп.
Преимущества рандомизации в исследованиях:
- Избегание смещения результатов: рандомизация позволяет ученым исключить возможное влияние внешних факторов или личных предпочтений при распределении участников или элементов исследования.
- Улучшение внешней валидности: случайное размещение может помочь ученым обобщить результаты своих исследований на более широкую популяцию, делая их результаты более репрезентативными.
- Получение более точных статистических выводов: использование рандомизации позволяет ученым сделать более точные статистические выводы о причинно-следственных связях между переменными и оценить степень статистической значимости полученных результатов.
Практическое применение рандомизации:
Рандомизация широко используется в различных областях исследований и практики. Например:
- В медицинских исследованиях рандомизация используется для распределения пациентов на разные группы лечения или препаратов. Это позволяет ученым оценить эффективность или безопасность нового лекарства, устройства или метода лечения.
- В психологических исследованиях рандомизация может применяться для распределения участников на разные условия эксперимента или для создания контрольной группы.
- В социологических исследованиях рандомизация может использоваться для случайного отбора респондентов из определенной популяции и минимизации искажений и влияний личных предпочтений при проведении опросов или анкетирования.
В конечном итоге, рандомизация играет важную роль в повышении достоверности исследований и обеспечении более точных результатов. Она помогает исключить возможное смещение и внешние факторы, а также делает возможными более точные статистические выводы и обобщение результатов на более широкую популяцию.
Важность параметра порядка в различных сферах
Параметр порядка является важным понятием во многих областях, где необходимо упорядочить или классифицировать элементы. Он позволяет определить последовательность или приоритетность элементов на основе определенных критериев.
В различных сферах параметр порядка играет важную роль:
В программировании: параметр порядка используется для определения очередности выполнения операций или функций. Например, в алгоритмах сортировки элементов массива параметр порядка позволяет установить приоритетность элементов в зависимости от их значений
Также параметр порядка может быть использован для определения порядка выполнения действий в программе.
В бизнесе: в различных сферах бизнеса, таких как управление проектами или продажи, параметр порядка используется для определения важности задач, приоритетов или стадий выполнения проекта. Например, при составлении календарного плана проекта каждой задаче присваивается параметр порядка, который указывает, в каком порядке задачи должны быть выполнены.
В маркетинге: параметр порядка может быть использован для определения порядка отображения рекламных объявлений или предложений на веб-странице или в электронной почте
Например, в поисковых системах параметры порядка используются для расположения объявлений в результатах поиска, где очень важно отобразить наиболее релевантные объявления сверху списка.
В науке: параметр порядка имеет особое значение в статистике и исследованиях. В статистике параметры порядка могут использоваться для классификации данных и определения приоритетов. В исследованиях параметр порядка может использоваться для установления связей между переменными и определения значимости этих связей.
Важность параметра порядка в различных сферах подчеркивает его универсальность и значимость при работе с различными видами данных и элементами. Он помогает упорядочить, классифицировать и определить приоритетность элементов, что способствует более эффективному и структурированному решению задач в различных областях
Важность произвольного порядка в математике
Произвольный порядок в математике играет важную роль в решении различных задач и задачах, связанных с комбинаторикой и вероятностью. Он позволяет рассмотреть все возможные варианты расположения элементов в некотором множестве и определить количество таких вариантов.
Произвольный порядок особенно полезен при решении задач, связанных с перестановками и сочетаниями. Перестановка — это упорядоченное расположение элементов, а сочетание — неупорядоченное. Зная количество элементов и размеры групп, можно использовать произвольный порядок для определения количества различных перестановок и сочетаний.
Например, если имеется множество из 5 элементов, то количество возможных перестановок будет равно факториалу числа 5 (5!). Если же требуется найти количество сочетаний из этого множества по 3 элемента, то используется формула сочетаний с повторениями, которая также зависит от произвольного порядка.
Таким образом, произвольный порядок является важным инструментом в математике, позволяющим анализировать и решать различные задачи, связанные с перестановками, сочетаниями и другими комбинаторными объектами.
Виды последовательности
Последовательность может быть ограниченной или неограниченной, возрастающей или убывающей.
Последовательность (Xn) называет ограниченной,
если существуют два числа m и M такие, что для любого n принадлежащего множеству натуральных чисел, будет выполняться равенство m
Последовательность (Xn), не являющаяся ограниченной,
называется неограниченной последовательностью.
возрастающей,
если для всех натуральных n выполняется следующее равенство X(n+1) > Xn. Другими словами, каждый член последовательности, начиная со второго, должен быть больше предыдущего члена.
Последовательность (Xn) называется убывающей,
если для всех натуральных n выполняется следующее равенство X(n+1)
Таблицы (датафреймы)
— базовый для R формат, который используется для представления таблиц. В R поддерживается классическая концепция таблиц, характерная для социальных наук и data science, когда по строкам расположены наблюдения, а колонки образуют пространство признаков этих наблюдений. На уровне структуры — это всё те же списки, в которых могут храниться разные по типу объекты, однако с требованием равенства длины объектов
Важно: все значения одной колонки могут быть только одного типа, а не как в Excel, OpenOffice или другом табличном процессоре
Таблицы можно создать с помощью функции , где аналогично созданию списка через запятую перечисляются векторы, значения которых будут представлены в виде колонок (использование списков для формирования колонок возможно, но встречается реже и несколько сложнее в последующем использовании). Так как все колонки должны быть одной длины, то и длины векторов соответственно должны быть одинаковы. Возможны и другие варианты создания -объектов путем преобразования из других объектов с помощью функции .
Предел последовательности
Предел последовательности
— это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности, для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Фундаментальные последовательности
Фундаментальная последовательность
(сходящаяся в себе последовательность
, последовательность Коши
) — это последовательность элементов метрического пространства , в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного. Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.
Объяснение концепции параметра порядка
Параметр порядка – это один из важных элементов в программировании, который позволяет управлять последовательностью выполнения определенных действий или операций.
Основная идея параметра порядка заключается в том, что разные операции или функции должны выполняться в определенном порядке или последовательности для обеспечения правильного результаты работы программы.
Когда мы задаем параметр порядка, мы указываем программе, в каком порядке и какие операции нужно выполнить, чтобы достичь желаемого результата. Без учета порядка, операции могут быть выполнены в случайном порядке или в неправильной последовательности, что может привести к непредсказуемым результатам или ошибкам.
В программировании параметр порядка может иметь разные форматы. Часто это просто числовые значения, но также может быть строковое значение или даже объект. Например, в языке программирования Python можно использовать индексацию для указания порядка выполнения операций.
Пример использования параметра порядка может быть в сценарии игры, где игроку нужно выполнить определенные действия в правильной последовательности. Например, передвинуть объект А, затем открыть дверь, а потом собрать предмет B. Если игрок выполнит эти действия в неправильном порядке, то может быть невозможно пройти дальше или достичь следующего уровня.
Это примерно объясняет, как работает и зачем нужен параметр порядка в программировании. Он позволяет контролировать последовательность выполнения операций и обеспечивать правильный результат работы программы.
Обратная перестановка
Обратной перестановкой называется перестановка, в которой каждый элемент поменялся местами с элементом, оригинально стоявшим на его индексе. Иными словами, обратная перестановка является результатом инвертирования порядка элементов в исходной перестановке.
Для примера рассмотрим следующую перестановку из пяти элементов: 4 2 5 1 3. Чтобы получить обратную перестановку, мы поменяем каждый элемент местами с тем элементом, который оригинально стоял на его индексе.
Таким образом, обратная перестановка будет выглядеть следующим образом: 4 5 1 3 2. Элементы 2 и 5 поменялись местами, элементы 1 и 4 поменялись местами, и т. д.
Обратная перестановка является обратной операцией к исходной перестановке. Если мы снова применим операцию обратной перестановки к полученной обратной перестановке, то снова получим исходную перестановку.
Обратная перестановка широко используется в различных алгоритмах сортировки и шифрования данных. Знание о концепции обратной перестановки помогает понять их работу и эффективность.
Порядок перестановки: основные понятия
Перестановка — это упорядоченный набор элементов, в котором каждый элемент занимает определенное место. Порядок перестановки определяет, сколько раз нужно применить перестановку, чтобы вернуть все элементы в исходное положение.
Порядок перестановки является одним из основных понятий теории групп и комбинаторики. Он широко используется в различных областях, таких как математика, криптография, алгоритмы и другие.
Имеется несколько способов определить порядок перестановки. Один из них — это количество элементов в перестановке. Например, если перестановка содержит 4 элемента, то ее порядок будет равен 4.
Другой способ определения порядка перестановки — это нахождение наименьшего общего кратного всех циклических длин перестановки. Циклическая длина перестановки — это количество элементов, которые не меняются местами при применении перестановки.
Например, рассмотрим перестановку (1 2 3 4). Она имеет следующие циклические длины: 1, 1, 1, 1. Наименьшее общее кратное этих длин равно 1, поэтому порядок данной перестановки равен 1.
Для наглядности, порядок перестановки может быть представлен в виде таблицы, где каждая строка соответствует одному циклу:
| Перестановка | Циклические длины | Порядок |
|---|---|---|
| (1 2 3 4) | 1, 1, 1, 1 | 1 |
| (1 2)(3 4) | 2, 2 | 2 |
| (1 2 3) | 3 | 3 |
Из таблицы видно, что различные перестановки могут иметь разный порядок. Например, перестановка (1 2)(3 4) имеет порядок 2, потому что циклические длины равны 2 и 2.
Порядок перестановки является важным свойством, которое может использоваться для анализа и решения различных задач, связанных с перестановками.
Как использовать произвольный порядок чисел
1. Изучение материала
При изучении нового материала или концепции можно использовать произвольный порядок чисел, чтобы сделать процесс более интересным и эффективным. Вместо традиционного линейного порядка, вы можете представить информацию в произвольном порядке, что поможет активизировать мозг и улучшит вашу способность к запоминанию и пониманию.
2. Организация задач
Произвольный порядок чисел может быть полезен при организации задач или списков дел. Вы можете пронумеровать задачи в случайном порядке, вмешивая более сложные и менее сложные задачи друг с другом. Это поможет вам сохранить интерес и мотивацию при выполнении задач и предотвратит чувство монотонности или утомления.
3. Создание презентаций
Произвольный порядок чисел может быть полезным при создании презентаций или выступлений. Вместо простого линейного порядка слайдов или информации, вы можете использовать произвольный порядок, чтобы создать более динамичную и интересную презентацию
Это поможет привлечь внимание слушателей и сделать вашу презентацию запоминающейся
Также, важно помнить, что произвольный порядок чисел не подходит для всех случаев. Некоторые задачи или материалы могут требовать строгой логической последовательности
При использовании произвольного порядка, стоит быть внимательным и адаптировать его под конкретную ситуацию.
В итоге, произвольный порядок чисел является мощным инструментом, который может быть использован для активизации мозга, улучшения запоминания и создания интересных презентаций. Экспериментируйте с этим методом и найдите способы его применения в своей повседневной жизни и работе.
Повышение когнитивной гибкости
Использование произвольного порядка чисел помогает тренировать мозг на многозадачность, улучшает память, концентрацию и внимание. Когда мы вынуждены упорядочивать числа в произвольном порядке, наше внимание активируется, что способствует улучшению когнитивных функций
При использовании произвольного порядка чисел в тренировке мышления мы вынуждены разбивать сложные задачи на более простые подзадачи, а затем упорядочивать их нестандартным образом. Это требует от нас гибкого и глубокого мышления, поскольку у нас может не быть однозначного правильного ответа.
Произвольный порядок чисел также укрепляет связи между нейронами в нашем мозгу, улучшая его пластичность и эластичность. Это позволяет нам обучаться и адаптироваться быстрее, лучше решать проблемы и находить новые пути решения.
Итак, использование произвольного порядка чисел в тренировке мышления и повседневной жизни помогает нам развивать и повышать нашу когнитивную гибкость, что в свою очередь способствует улучшению наших когнитивных функций и способностей.
Сходимость и пределы
ничего не
происходит
никогда не остановитсяникогда его не достигнет
сходитсяпределомбесконечно малой
подобрать
при отрицательном приросте населения город вымирает
3.2. Бесконечно большие последовательности
нет
бесконечно большой
стремится к бесконечностистремится к плюс бесконечностистремится к минус бесконечности
осциллирующими
3.3. Подпоследовательности и частичные пределы
подпоследовательностью
не является
статью о множествах
частичным пределом
частичным пределом
он тоже
вселюбое бесконечное число точек
периодическая
абсолютно все
3.4. Верхний и нижний пределы
верхнийнижний пределы
Внимание! Статья
в разработке. Возможно, я дописываю её прямо сейчас
Так что ждите
продолжения! (Нажмите Поддержать проект, чтобы узнать, как можно ускорить
этот процесс.)
3.5. Монотонность последовательностей
Внимание! Статья
в разработке. Возможно, я дописываю её прямо сейчас
Так что ждите
продолжения! (Нажмите Поддержать проект, чтобы узнать, как можно ускорить
этот процесс.)
Свойства величин последовательностей
Казалось бы, предел числовой последовательности уже разобран довольно подробно, однако не раз упоминаются такие фразы, как «бесконечно маленькие» и «бесконечно большие» числа. Очевидно, если есть последовательность 1/х, где x→∞, то такая дробь бесконечно малая, а если та же последовательность, но предел стремится к нулю (х→0), то дробь становится бесконечно большой величиной. А у таких величин есть свои особенности. Свойства предела последовательности, имеющей какие угодно малые или большие величины, состоят в следующем:
- Сумма любого количества сколько угодно малых величин будет также малой величиной.
- Сумма любого количества больших величин будет бесконечно большой величиной.
- Произведение сколь угодно малых величин бесконечно мало.
- Произведение сколько угодно больших чисел — величина бесконечно большая.
- Если исходная последовательность стремится к бесконечно большому числу, то величина, ей обратная, будет бесконечно малой и стремиться к нулю.
На самом деле вычислить предел последовательности — не такая сложная задача, если знать простой алгоритм. Но пределы последовательностей — тема, требующая максимума внимания и усидчивости. Конечно, достаточно просто уловить суть решения подобных выражений. Начиная с малого, со временем можно достигнуть больших вершин.
Числовой
последовательностью
называется
числовая функция, определенная на
множестве натуральных чисел
.
Если
функцию
задать на множестве натуральных чисел ,
,
то множество значений функции будет
счетным и каждому номеру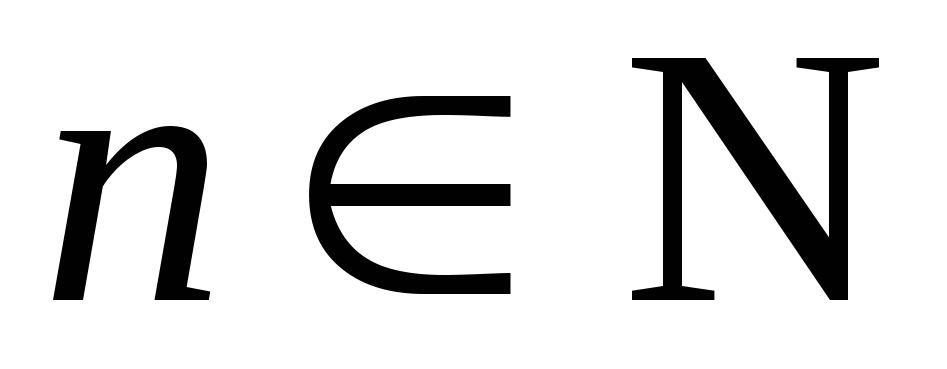 ставится в соответствие число
ставится в соответствие число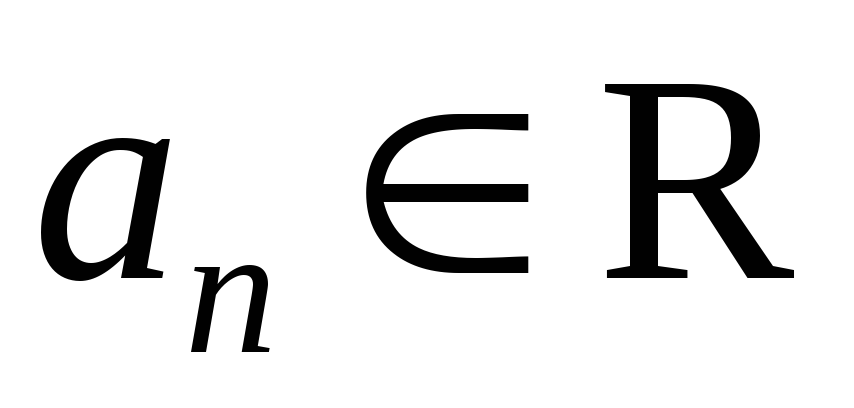 .
.
В этом случае говорят, что заданачисловая
последовательность
. Числаназываютэлементами
или членами
последовательности, а число – общим или
– общим или –м
–м
членом последовательности. Каждый
элемент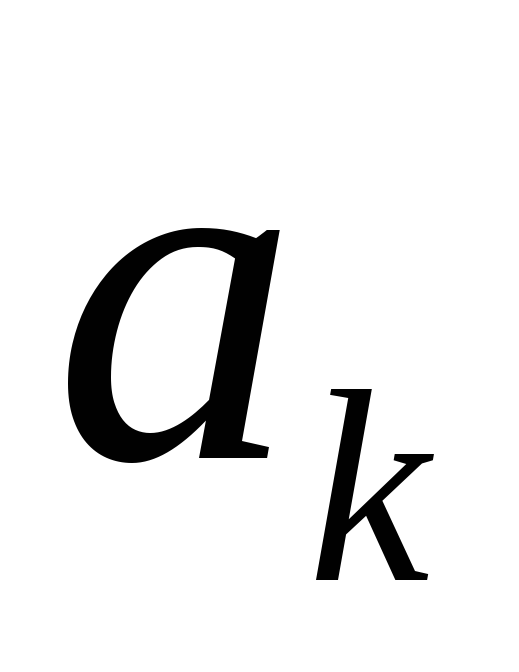 имеет последующий элемент
имеет последующий элемент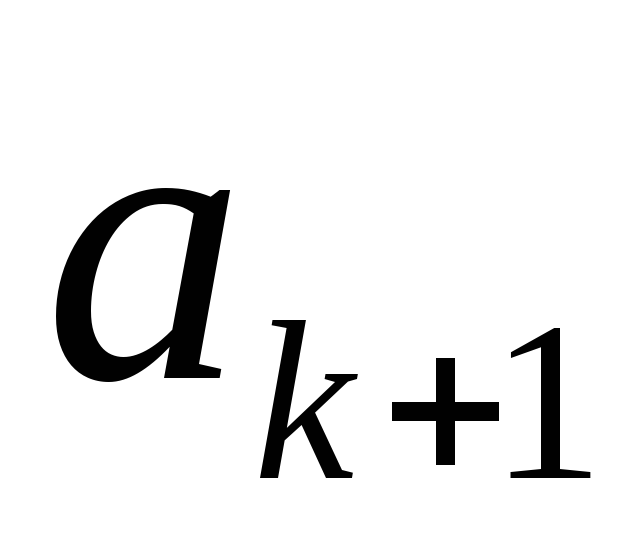 .
.
Это объясняет употребление термина
«последовательность».
Задают
последовательность обычно либо
перечислением ее элементов
,
либо указанием закона, по которому
вычисляется элемент с номером ,
,
т.е. указанием формулы ее ‑го
‑го
члена .
.
Пример.
Последовательность
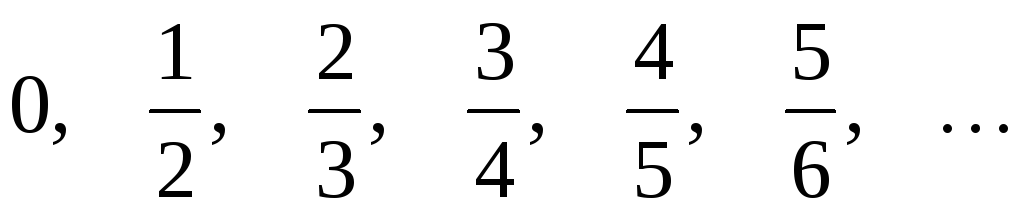 может быть задана формулой
может быть задана формулой
: .
.
Обычно
последовательности обозначаются так:
и т.п., где в скобках указывается формула
ее -го
-го
члена.
Пример.
Последовательность
 ‑это последовательность
‑это последовательность
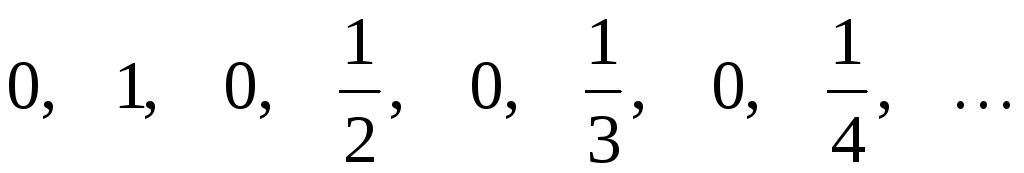
Множество
всех элементов последовательности
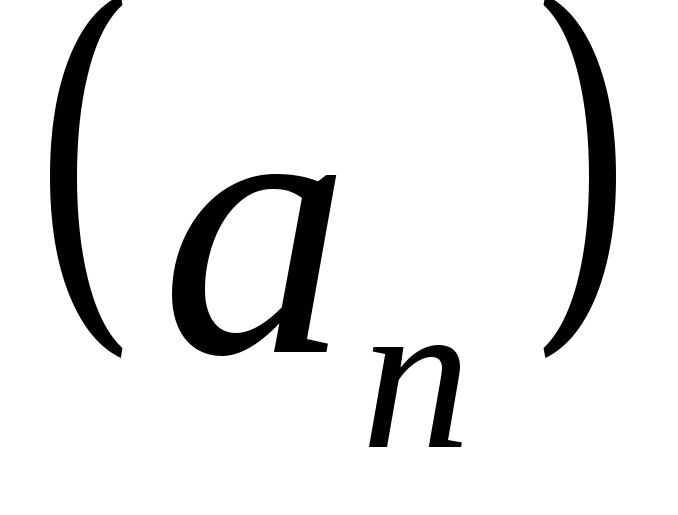 обозначается
обозначается .
.
Пусть
 и
и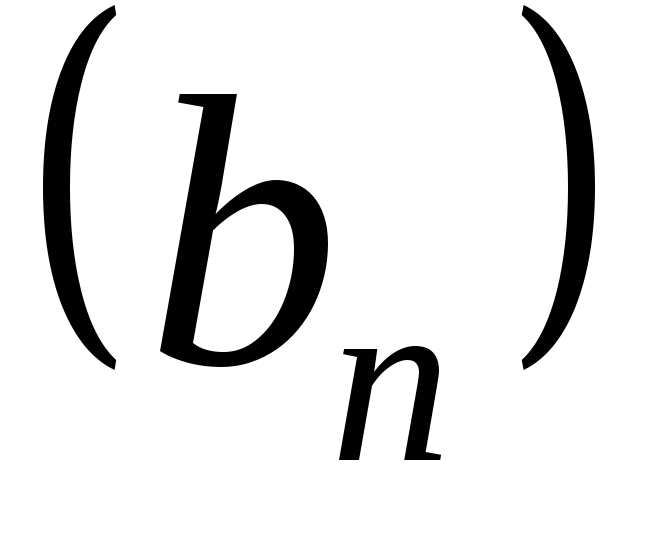 ‑ две последовательности.
‑ две последовательности.
Суммой
последовательностей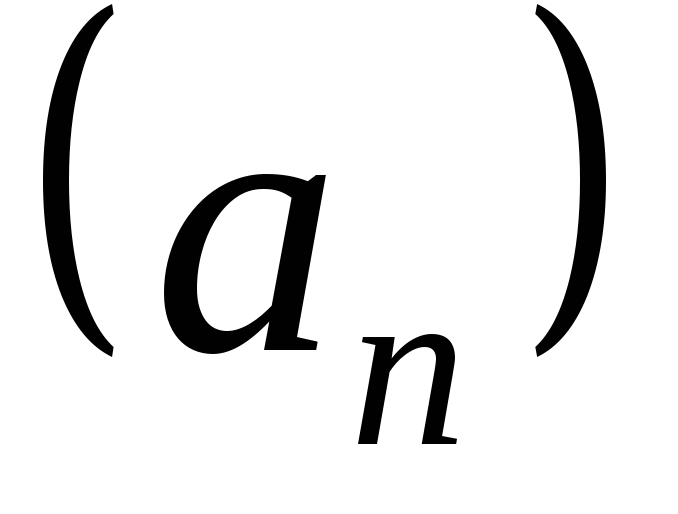 и
и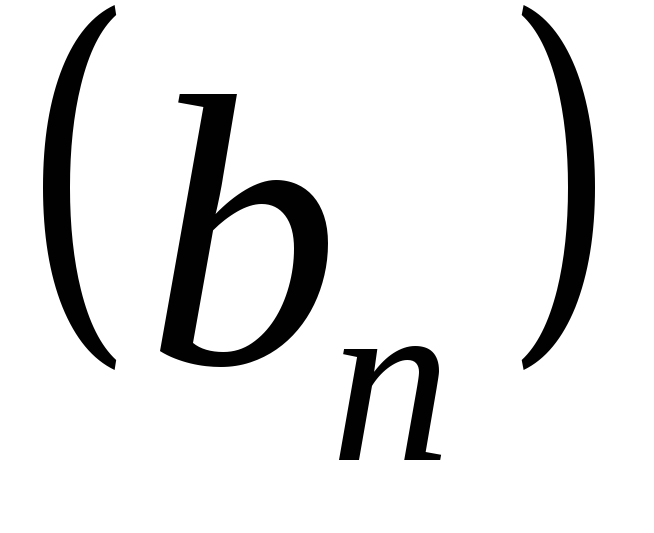 называют последовательность
называют последовательность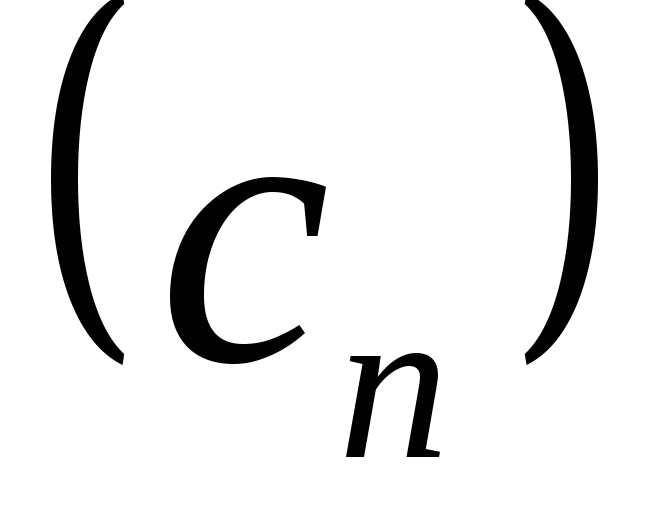 ,
,
где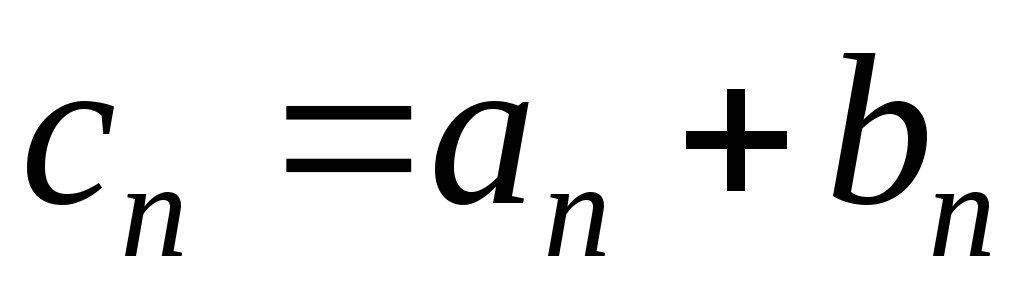 ,
,
т.е..
Разностью
этих последовательностей называют
последовательность ,
,
где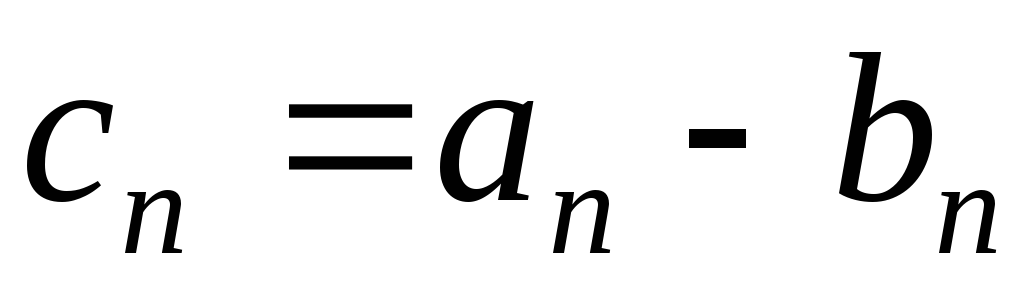 ,
,
т.е..
Если
 и
и
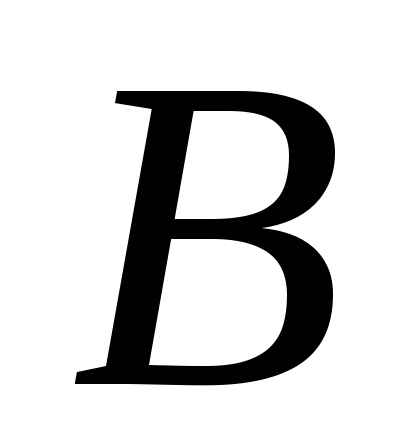 ‑
‑
постоянные, то последовательность
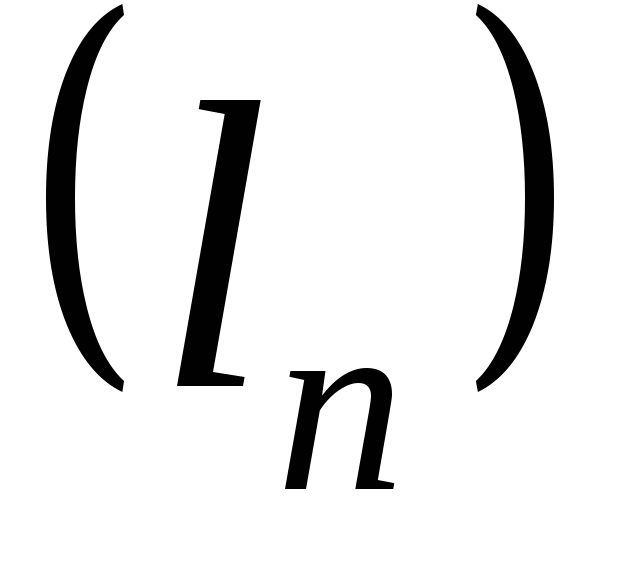 ,
,
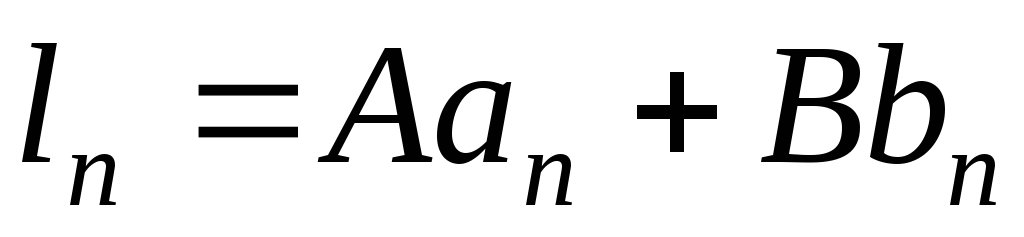 называютлинейной комбинацией
называютлинейной комбинацией
последовательностей и
и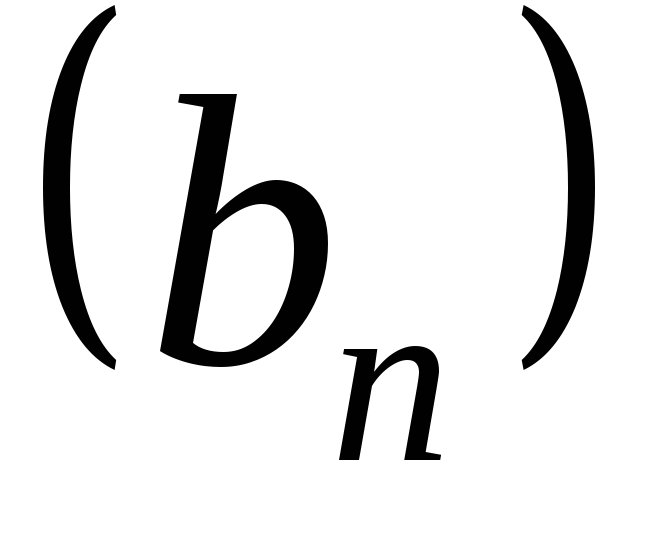 ,
,
т.е.
Произведением
последовательностей и
и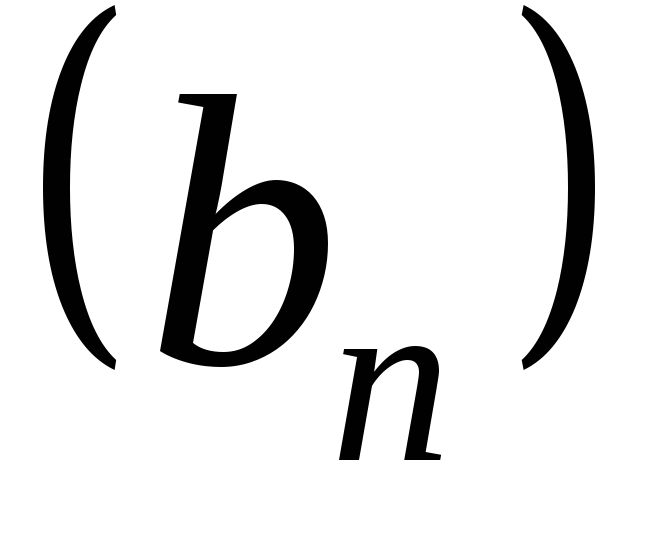 называют последовательность с
называют последовательность с -м
-м
членом ,
,
т.е.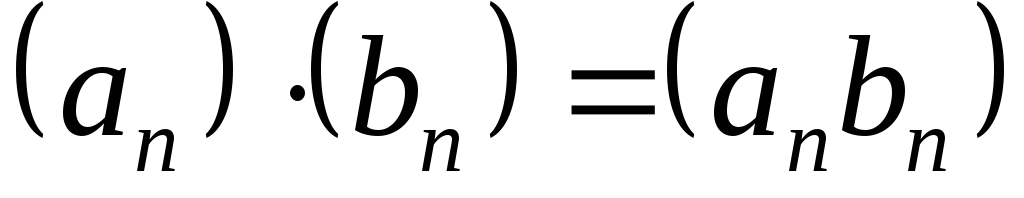 .
.
Если
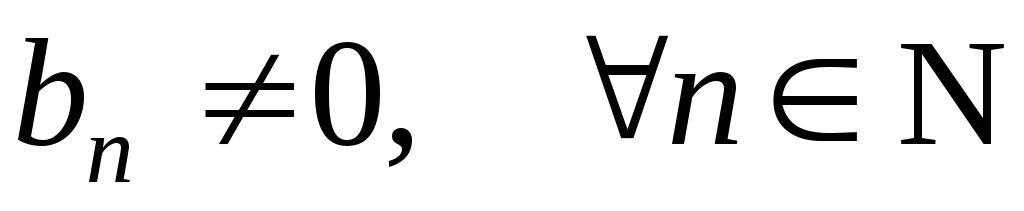 ,
,
то можно определитьчастное
 .
.
Сумма,
разность, произведение и частное
последовательностей
 и
и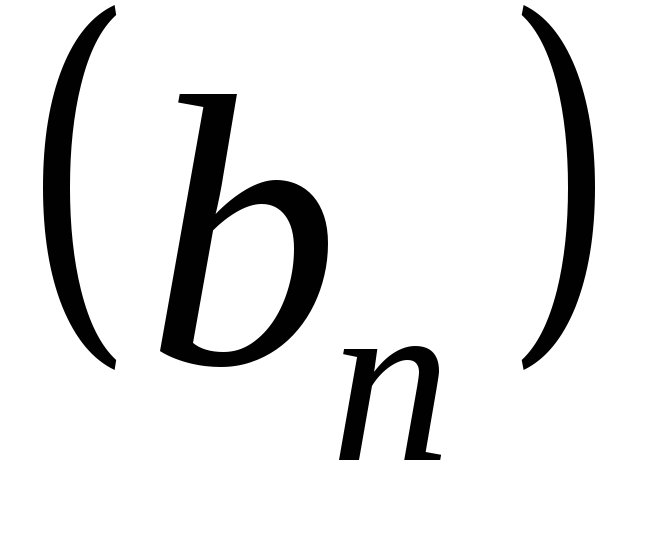 называются ихалгебраическими
называются ихалгебраическими
композициями
.
Пример.
Рассмотрим последовательности
 и
и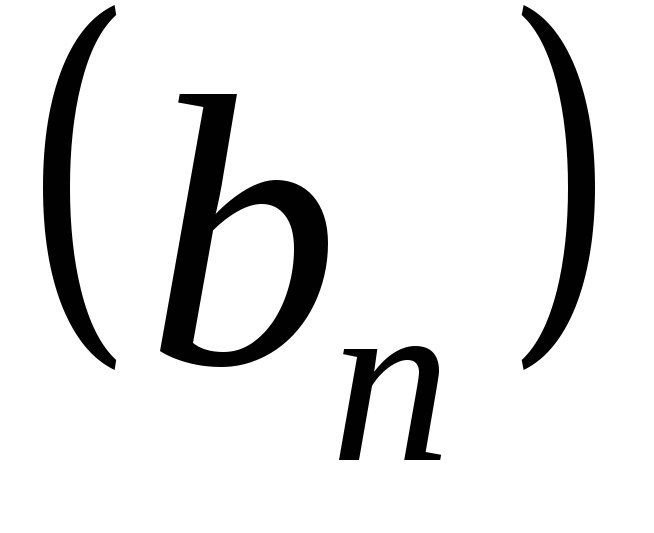 ,
,
где.
Тогда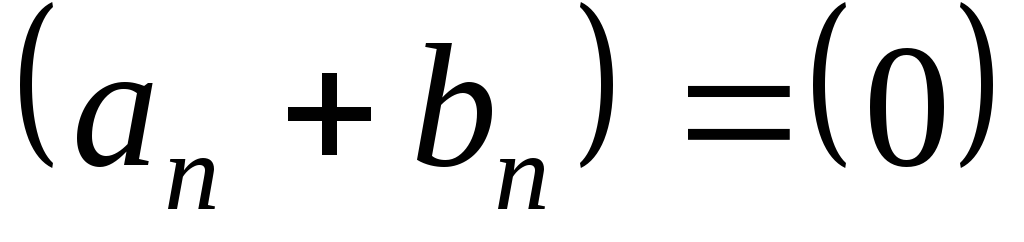 ,
,
т.е. последовательность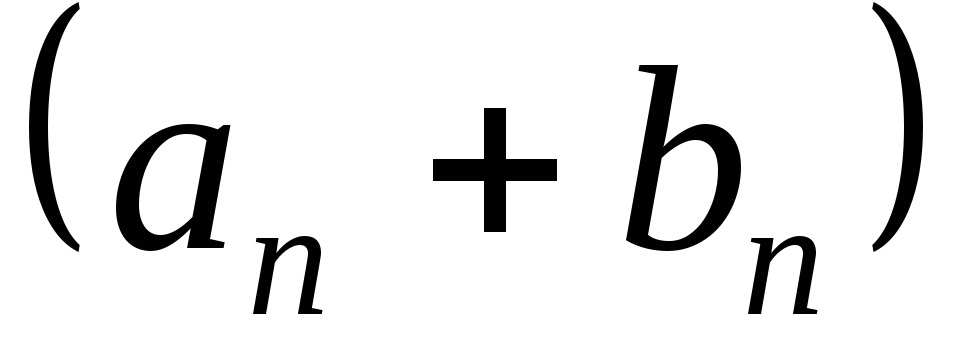 имеет все элементы, равные нулю.
имеет все элементы, равные нулю.
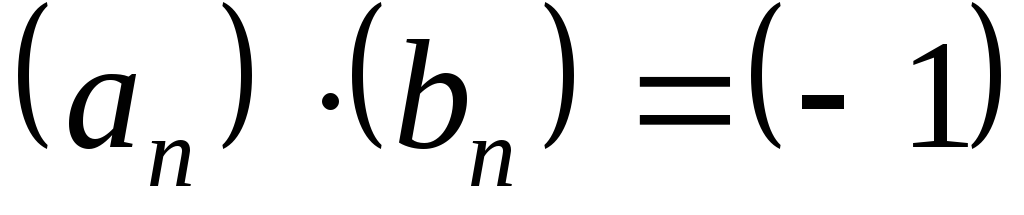 ,
,
 ,
,
т.е. все элементы произведения и частного
равны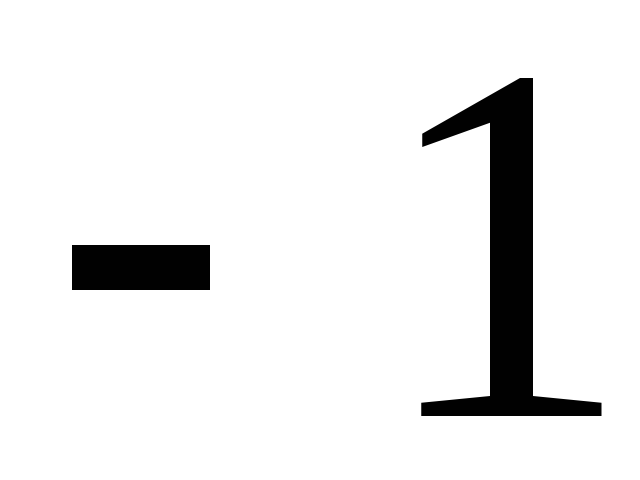 .
.
Если
вычеркнуть некоторые элементы
последовательности
 так, чтобы осталось бесконечное множество
так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемуюподпоследовательностью
последовательности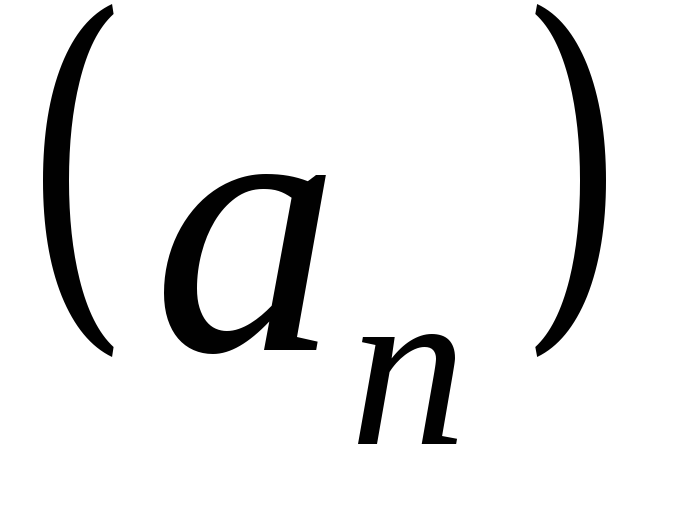 .
.
Если вычеркнуть несколько первых
элементов последовательности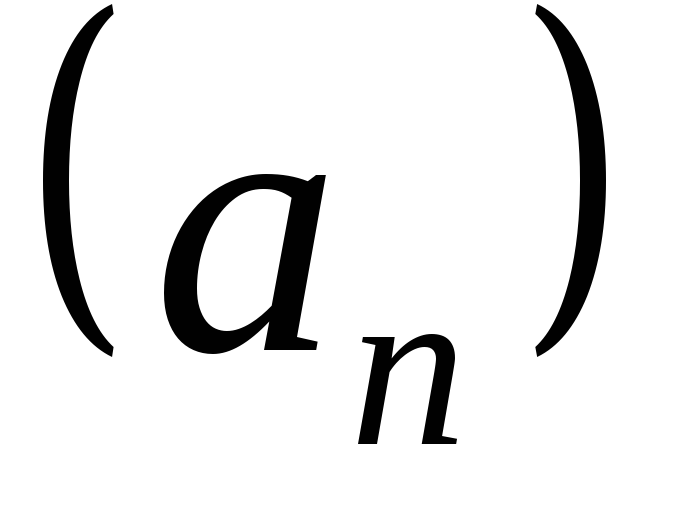 ,
,
то новую последовательность называютостатком
.
Последовательность
 ограничена
ограничена
сверху
(снизу
),
если множество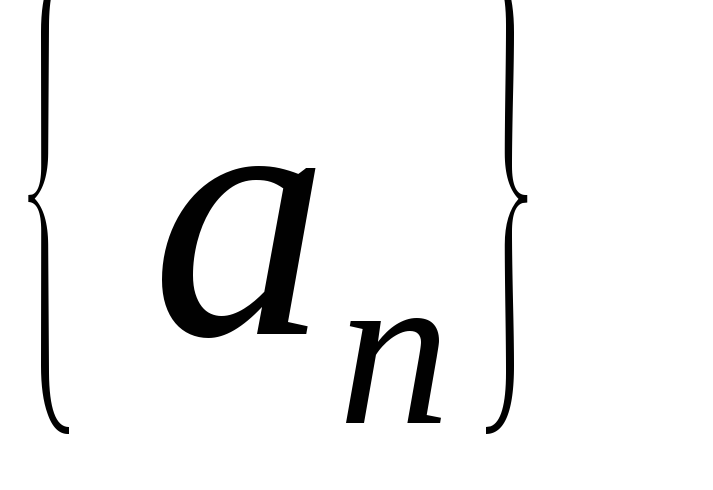 ограничено сверху (снизу). Последовательность
ограничено сверху (снизу). Последовательность
называютограниченной
, если она
ограничена сверху и снизу. Последовательность
ограничена тогда и только тогда, когда
ограничен любой ее остаток.
Алгоритмы рандомизации
Рандомный порядок — это порядок элементов или событий, который не имеет определенной закономерности и определяется случайным образом. Для создания рандомного порядка существуют различные алгоритмы рандомизации. Ниже приведены некоторые из них.
- Алгоритм Фишера-Йетса — один из самых распространенных алгоритмов рандомизации. Он основан на перестановке элементов в массиве. Алгоритм прост и эффективен — он проходит по массиву от конца к началу и на каждом шаге меняет текущий элемент с случайно выбранным элементом до текущей позиции.
-
Алгоритм Кнута — еще один известный алгоритм рандомизации, разработанный Дональдом Кнутом. Он использует генератор псевдослучайных чисел, чтобы определить случайные перестановки элементов. Алгоритм Кнута обеспечивает равновероятное появление каждого элемента на любой позиции.
-
Алгоритм Мерсенна — это алгоритм рандомизации, основанный на числах Мерсенна. Числа Мерсенна — это числа, представленные в виде 2^n — 1, где n — простое число. Алгоритм Мерсенна использует такие числа для выбора случайных перестановок элементов.
Независимо от выбранного алгоритма рандомизации, важно помнить, что рандомный порядок может быть получен только путем использования алгоритма, который представляет случайные значения. В противном случае можно получить порядок, который имеет определенный шаблон или закономерность, и не является истинно рандомным
Примеры
Упорядоченные последовательности
Одним из простейших примеров упорядоченной последовательности является натуральный ряд 1, 2, 3, 4, 5, … . Каждый следующий элемент этой последовательности равен предыдущему плюс единица.
Другой пример упорядоченной последовательности – арифметическая прогрессия. В этой последовательности каждый следующий элемент определяется по формуле an = an-1 + d, где an – текущий элемент, an-1 – предыдущий, а d – разность между элементами.
Неупорядоченные последовательности
Примером неупорядоченной последовательности является множество цветов радуги – красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Эти элементы не имеют строгого порядка, каждый элемент является сам по себе и не зависит от других элементов множества.
Еще одним примером неупорядоченной последовательности являются слова в словаре. Они просто отсортированы по алфавиту и не имеют логической связи между собой.
Частично упорядоченные последовательности
Примером частично упорядоченной последовательности является множество чисел, где некоторые элементы можно сравнить между собой, а некоторые нет. Например, в множестве (-1, 0, 1) число 1 больше числа 0, а число 0 больше числа -1. Однако сравнить числа -1 и 1 нельзя, так как они находятся по разные стороны от нуля.
Еще одним примером может служить множество слов, где некоторые слова можно отнести к одной категории, например, «собака», «кошка», «хомяк» – как домашние животные, а другие слова этой категории не принадлежат, например, «слон» или «тигр».
Одно- и многомерные последовательности
Одномерной упорядоченной последовательностью может служить, например, список покупок в магазине – муть, тофу, чеснок, сыр, яблоки.
Многомерной упорядоченной последовательностью может служить, например, таблица умножения, где каждый элемент определяется парой чисел.
Таблица умножения:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 6 | 8 | 10 |
| 3 | 3 | 6 | 9 | 12 | 15 |
| 4 | 4 | 8 | 12 | 16 | 20 |
| 5 | 5 | 10 | 15 | 20 | 25 |
Предел последовательности.
Пусть есть последовательность {c n
} = {1/n
}.Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a
и b
есть число
В противном случае последовательность называется расходящейся.
Опираясь на это определение, можно, например, доказать наличие предела A = 0
у гармонической последовательности {c n
} =
{1/n
}. Пусть ε – сколь угодно малое положительное число. Рассматривается разность
Существует ли такое N
, что для всех n ≥
N
выполняется неравенство 1/N ? Если взять в качестве N
любое натуральное число, превышающее1/ε
, то для всех n ≥ N
выполняется неравенство 1/n ≤
1/N ε ,что и требовалось доказать.
Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.
Теорема 1. Если последовательность имеет предел, то она ограничена.
Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.
Теорема 3. Если последовательность {a n
}имеет предел A
, то последовательности {ca n
}, {a n
+ с}и {| a n
|}имеют пределы cA
, A
+ c
, |A
| соответственно (здесь c
– произвольное число).
Теорема 4. Если последовательности {a n
}и {b n
} имеют пределы, равные A
и B
pa n
+ qb n
} имеет предел pA
+ qB
.
Теорема 5. Если последовательности {a n
} и {b n
}имеют пределы, равные A
и B
соответственно, то последовательность {a n b n
} имеет предел AB.
Теорема 6. Если последовательности {a n
}и {b n
} имеют пределы, равные A
и B
соответственно, и, кроме того, b n ≠
0 и B ≠
0, то последовательность {a n / b n
} имеет предел A/B
.
Анна Чугайнова



























