Системы линейных уравнений
Напоминание теории. Системой линейных алгебраических уравнений
называется система вида , где
.
В случае квадратной невырожденной матрицы решение системы
единственно.
В NumPy решение такой системы можно найти с помощью функции
numpy.linalg.solve(a, b), где первый аргумент — матрица
, второй — столбец .
a = np.array(, 1, 2]]) b = np.array() x = np.linalg.solve(a, b)
print (a.dot(x))
Бывают случаи, когда решение системы не существует. Но хотелось бы все
равно “решить” такую систему. Логичным кажется искать такой вектор
, который минимизирует выражение
— так мы приблизим выражение
к .
В NumPy такое псевдорешение можно искать с помощью функции
numpy.linalg.lstsq(a, b, …), где первые два аргумента такие
же, как и для функции numpy.linalg.solve(). Помимо решения
функция возвращает еще три значения, которые нам сейчас не понадобятся.
a = np.array(, 1, 1], 2, 1], 3, 1]]) b = np.array() x, res, r, s = np.linalg.lstsq(a, b, rcond=None)
Умножение матриц
Пример 7
. Даны матрицы и . Найти матрицы C = A·B и D = B·A.Решение.
Прежде всего заметим, что произведение A·B существует, так как число столбцов A равно числу строк B.
Пример 8
. Дана матрица . Найти 3A 2 – 2A.Решение.
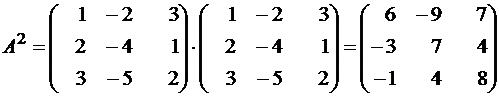 .
.
; .
.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.
С каждой
квадратной матрицей связаны два многочлена: характеристический и минимальный.
Эти многочлены играют большую роль в различных вопросах теории матриц. Так,
например, понятие о функции от матрицы, которое мы введем в следующей главе,
будет целиком основываться на понятии о минимальном многочлене матрицы. В этой
главе рассматриваются свойства характеристического и минимального многочлена.
Этому исследованию предпосылаются основные сведения о многочленах с матричными
коэффициентами и о действиях над ними.
§ 1. Сложение и умножение матричных многочленов
Рассмотрим
квадратную многочленную матрицу , т. е. квадратную матрицу, элементами
которой являются многочлены относительно (с коэффициентами из данного
числового поля ):
Матрицу можно представить
в виде многочлена с матричными коэффициентами, расположенного по степеням :
. (3)
Число называется степенью
многочлена, если .
Число называется
порядком многочлена. Многочлен (1) будем называть регулярным,
если .
Многочлен с
матричными коэффициентами мы будем иногда называть матричным многочленом.
В отличие от матричного многочлена обычный многочлен со скалярными
коэффициентами будем называть скалярным многочленом.
Рассмотрим
основные действия над матричными многочленами. Пусть даны два матричных
многочлена одного и того же порядка и . Обозначим через наибольшую из степеней этих
многочленов. Эти многочлены можно записать в виде
т. е. сумма
(разность) двух матричных многочленов одного и того же порядка может быть
представлена в виде многочлена, степень которого не превосходит наибольшей из
степеней данных многочленов.
Пусть даны два
матричных многочлена и степеней и одного и того же порядка :
Если бы мы
перемножили на
(т. е. изменили
бы порядок сомножителей), то мы получили бы, вообще говоря, другой многочлен.
Умножение
матричных многочленов обладает еще одним специфичным свойством. В отличие от
произведения скалярных многочленов произведение матричных многочленов (4) может
иметь степень, меньшую , т. е. меньшую суммы степеней
сомножителей. Действительно, в (4) произведение матриц может равняться нулю при и . Однако, если хотя
бы одна из матриц и неособенная, то из и следует: . Таким образом, произведение
двух матричных многочленов равно многочлену, степень которого меньше или равна
сумме степеней сомножителей. Если хотябы один из двух сомножителей регулярный
многочлен, то в этом случае степень произведения всегда равна сумме степеней
сомножителей.
Матричный
многочлен -го
порядка можно
записать двояко:
Обе записи при
скалярном дают
один и тот же результат. Однако если мы пожелаем вместо скалярного аргумента подставить
квадратную матрицу -го порядка , то результаты подстановок
в (5) и (5″) будут, вообще говоря, различны, так как степени матрицы могут не быть
перестановочными с матричными коэффициентами .
и будем называть
правым,
а левым
значением матричного многочлена при подстановке вместо матрицы .
Рассмотрим снова
два матричных многочлена
,
и их произведение
Преобразования в
тождестве (7″) сохраняют свою силу при замене матрицей -го порядка , если только
матрица перестановочна
со всеми матричными коэффициентами . Аналогично в тождестве (7″)
можно заменить скаляр матрицей , если матрица перестановочна со
всеми коэффициентами . В первом случае получаем: любой матрицей -го порядка всегда справедливы
тождества
, . (9)
>мерный вектор и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
Определение.-мерным вектором называется упорядоченная совокупность действительных чисел, записываемых в виде где — -я компонента вектора .
Понятие -мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором , а соответствующие цены — вектором
Два -мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. если
Суммой двух векторов одинаковой размерности п называется вектор компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е.
Произведением вектора на действительное число называется вектор , компоненты которого равны произведению на соответствующие компоненты вектора , т.е.
Линейные операции над любыми векторами удовлетворяют следующим свойствам:
- — коммутативное (переместительное) свойство суммы:
- — ассоциативное (сочетательное) свойство суммы;
- — ассоциативное относительно числового множителя свойство;
- — дистрибутивное (распределительное) относительно суммы векторов свойство;
- —дистрибутивное относительно суммы числовых множителей свойство;
- Существует нулевой вектор такой, что для любого вектора (особая роль нулевого вектора);
- Для любого вектора существует противоположный вектор такой, что
- для любого вектора (особая роль числового множителя 1).
Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
Следует отметить, что под можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством.
Линейным пространством является, например, множество всех алгебраических многочленов степени, не превышающей натурального числа Легко убедиться, что если х и у — многочлены степени не выше п, то они будут обладать свойствами 1—8. Заметим для сравнения, что, например, множество всех многочленов степени, точно равной натуральному числу , не является линейным пространством, так как в нем не определена операция сложения элементов, ибо сумма двух многочленов может оказаться многочленом степени ниже . А множество многочленов степени не выше , но с положительными коэффициентами также не является линейным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа.
Из определения векторного (линейного) пространства, в частности из аксиом 1-8, вытекает существование единственного нулевого вектора, равного произведению произвольного вектора на действительное число 0 и существование для каждого вектора единственного противоположного вектора (—), равного произведению этого вектора на действительное число (- 1).
Brilliant Math & Science Wiki
Энди Хейс,
Мехул Арора,
Хобарт Пао,
и
способствовал
Содержимое
- Идентификация полиномов
- Компоненты многочленов
- Степени многочленов
- Арифметика многочленов
- Факторные полиномы
- Полиномиальные функции
- Теоремы об остатках и факторах
- Тождества Ньютона
Многочлен — это особый тип математического выражения.
Некоторые из приведенных выше выражений являются полиномами (выделены синим цветом), а некоторые нет (красным цветом). Многочлены можно определить, отметив, какие выражения содержат только операций сложения, вычитания, умножения и неотрицательных целых показателей степени. Неполиномиальными выражениями будут выражения, содержащие другие операции.
Полиномы — это хорошо изученные математические объекты, поэтому математикам удобно иметь возможность выражать математические процессы в виде полиномов. Неполиномиальные выражения, как правило, представляют больше проблем при решении математических задач. В математическом анализе есть понятие, называемое приближением ряда Тейлора, целью которого является аппроксимация неполиномиального выражения в виде полиномиального выражения.![]()
Словарь многочленов поначалу может показаться немного пугающим. Однако эти «сложно звучащие» слова часто используются для обозначения простых идей.
«Стандартные блоки» полиномов называются мономами.
Обратите внимание, что каждый член может быть положительным или отрицательным, и этот знак зависит от того, был ли член добавлен в многочлен или вычтен из многочлена. Каждое слагаемое также имеет коэффициент
Обратите внимание, что значение коэффициента «по умолчанию» равно 111. Если термин не содержит переменных, то коэффициент является самим термином
Многочлены часто классифицируют по степени .
Многочлены классифицируются таким образом, потому что они демонстрируют различное математическое поведение и свойства в зависимости от степени. Степень полинома также влияет на стратегию решения задач для решения уравнений, содержащих этот полином.
![]()
Термины «постоянная», «линейная», «квадратичная» и «кубическая» широко распространены в математике; они используются не только в полиномах. Однако значение каждого из этих слов всегда связано со степенью некоторого полинома.
Многочлены представляют числа, поэтому любые математические операции могут выполняться над многочленами точно так же, как они выполняются над числами. Когда полиномы складываются, вычитаются или умножаются, результатом является другой полином. При делении многочленов результатом является рациональное выражение. 92-3x+8)(2×2-3x+8) и (x-3)(x-3)(x-3). Используйте полиномиальное деление, чтобы записать частное этих полиномов в виде суммы полинома и рационального выражения.
Полное деление выглядит следующим образом:
Таким образом, полученное частное равно 2x+3+17x−3,2x+3+\frac{17}{x-3},2x+3+x−317. □_\квадрат□
Разложение многочленов на множители — это процесс перезаписи многочлена как эквивалентного произведения многочленов.![]()
Приложения
Диагональность
Минимальный многочлен — мощный инструмент для определения диагонализируемости эндоморфизма.
Прогнозы
Проекция , в самом общем смысле, является эндоморфизмом таким, что:
Проекцию всегда можно диагонализовать. Фактически, взяв:
стоит . Отсюда следует, что оно принадлежит идеалу и, следовательно, делится на минимальный многочлен от . Так как оно имеет два корня и кратности , оно также имеет корни кратности , и поэтому оно диагонализируемо.
Инволюция — это такой эндоморфизм , что:
Точно так же это корень многочлена , который имеет два корня, которые различны, если характеристика поля отлична от . Так что это диагонально.
Использование жордановой формы для нахождения многочлена от матрицы
Использование жордановой формы матрицы для нахождения многочлена от матрицы основано на трех свойствах.
1. Многочлены от подобных матриц подобны.
Действительно, пусть при помощи преобразования подобия матрица приведена к жордановой форме . Подставим в правую часть (7.41):
Учитывая, что для любого натурального , получаем
Таким образом, многочлены и подобны (с той же самой преобразующей матрицей ):
2. Многочлен от блочно-диагоналъной матрицы является блочно-диагоналъной матрицей.
Пусть , где и — квадратные матрицы, а — нулевые матрицы соответствующих размеров. Для блочно-диагональных матриц справедливы равенства (они следуют из операций над блочными матрицами):
где
Поэтому .Для большего числа блоков доказательство V. о 1Аг)) аналогичное.
3. Многочлен (7.41) от жордановой клетки имеет вид
(7.42)
Это верхняя треугольная матрица r-го порядка, на главной диагонали которой стоят значения функции в точке , над диагональю — значения первой производной в этой же точке и т.д., т.е. коэффициенты ряда Тейлора для функции .
Действительно, разложим многочлен (7.40) по формуле Тейлора в окрестности точки
Остаточный член в данном случае равен нулю, так как все производные более высокого порядка, чем , тождественно равны нулю. При вычислении линейный двучлен заменяется матрицей
у которой элементы над главной диагональю равны единице, а остальные элементы равны нулю, т.е. , где — i-й столбец единичной матрицы r-го порядка.
Можно показать, что при возведении в степень единичные элементы матрицы смещаются вверх:
и т.д.
причем — нулевая матрица при . Подставляя эти матрицы в формулу Тейлора, получаем
Складывая матрицы в правой части, получаем квадратную матрицу r-го порядка, у которой элементы главной диагонали равны , элементы над главной диагональю равны — и т.д., т.е. матрицу вида (7.42).
Пример 7.16. Найти многочлен от матриц
Решение. а) Матрица — это жорданова клетка 3-го порядка, соответствующая собственному значению 2: . Находим значения функции и ее производных в точке . Составляем матрицу вида (7.42), учитывая, что
Матрица имеет жорданову форму , т.е. является блочно-диагональной. По свойству 2 многочлен от матрицы является блочно-диагональной матрицей. Записываем многочлен от каждой жордановой клетки по формуле (7.42):
Здесь число 7 рассматривается как квадратная матрица 1-го порядка. Составляем из этих квадратных матриц искомую блочно-диагональную матрицу
Матрица имеет жорданову форму , т.е. является блочно-диагональной. Записываем многочлен от каждой жордановой клетки по формуле (7.42):
Составляем из этих квадратных матриц искомую блочно-диагональную матрицу
Объединение массивов
Массивы можно Объединенять. Есть горизонтальное и вертикальное
объединение.
a = np.floor(10*np.random.random((2,2))) b = np.floor(10*np.random.random((2,2))) print(a) print(b) print() print(np.vstack((a,b))) print() print(np.hstack((a,b)))
] ] ] ]
Массивы можно переформировать при помощи метода, который задает новый
многомерный массив. Следуя следующему примеру, мы переформатируем
одномерный массив из десяти элементов во двумерный массив, состоящий из
пяти строк и двух столбцов:
a = np.array(range(10), float) print(a) print() # Превратим в матрицу a = a.reshape((5, 2)) print(a) print() # Вернем обратно print(a.flatten()) # Другой вариант print(a.reshape((-1))) # Превратим в марицу (9, 1) print(a.reshape((-1, 1))) # Превратим в марицу (1, 9) print(a.reshape((1, -1)))
] ] `0`.` 1`.` 2`.` 3`.` 4`.` 5`.` 6`.` 7`.` 8`.` 9`.``
Подходить на собственном примере
Рассмотрим вещественное векторное пространство размерности 3 с базой B = ( e 1 , e 2 , e 3 ). Рассмотрим затем эндоморфизм u, определяемый его следующим матричным представлением в базе B :
- ты(39-9233-3){\ displaystyle u: \; {\ begin {pmatrix} 3 & 9 & -9 \\ 2 & 0 & 0 \\ 3 & 3 & -3 \ end {pmatrix}}}
Вычисляя матричное представление u 2, а затем u 3 , находим:
- ты2(618-18618-18)етты3().{\ displaystyle u ^ {2}: \; {\ begin {pmatrix} 0 & 0 & 0 \\ 6 & 18 & -18 \\ 6 & 18 & -18 \ end {pmatrix}} \ quad и \ quad u ^ {3}: \; {\ begin {pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}}.}
Поскольку u 3 — нулевой эндоморфизм, u действительно нильпотентен с индексом 3.
Нильпотентность и многочлены
Затем определим характеристический многочлен P эндоморфизма u :
- п(Икс)знак равноDet(ты-Икся)знак равно|3-Икс9-92-Икс33-3-Икс|знак равно-Икс(3-Икс)(-3-Икс)-2(9(-3-Икс)+27)-27Иксзнак равно-Икс3.{\ Displaystyle P (X) = \ det (u-XI) = \; {\ begin {vmatrix} 3-X & 9 & -9 \\ 2 & -X & 0 \\ 3 & 3 & -3-X \ end {vmatrix}} = — X (3-X) (- 3-X) -2 (9 (-3-X) +27) -27X = -X ^ {3}.}
Имеет место равенство P ( X ) = — X 3 . В случае, когда размерность векторного пространства равна n , необходимым и достаточным условием для того, чтобы эндоморфизм был нильпотентным, является то, что его характеристический многочлен равен (- X ) n .
Теория минимальных многочленов говорит нам, что вычисление характеристического многочлена в этом примере не требуется. Многочлен X 3 отменяет эндоморфизм. Тогда минимальный многочлен является делителем этого многочлена. Однако единственный нормированный делитель (то есть чей моном высшей степени равен 1) числа — X 3, который сокращает u, является самим собой. Теорема Кэли-Гамильтона говорит нам, что минимальный многочлен делит характеристический многочлен. Тогда достаточно заметить, что характеристический многочлен имеет степень, равную размерности пространства, чтобы получить его без вычислений. Необходимым и достаточным условием нильпотентности эндоморфизма является то, что его минимальный многочлен имеет вид X p .
Нильпотентность и уменьшенная база
Рассмотрим тогда вектор e 1 . равен 3 , и семейство ( е 1 , у ( е 1 ), у 2 ( е 1 )) является свободным . Причем его кардинал — размерность пространства. Таким образом, эта семья является базой. В этой базе данных матричное представление u принимает следующий вид:
- ты(11).{\ displaystyle u: \; {\ begin {pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \ end {pmatrix}}.}
Опять же, эти свойства являются общими для нильпотентного эндоморфизма. В общем случае размерности n , если x является вектором индекса p, то p меньше или равно n и семейство ( x , u ( x ),…, u p-1 ( x )) является свободным. Кроме того, всегда существует базис ( e 1 , e 2 ,…, e n ) такой, что u ( e i ) равно либо 0, либо e i +1 , причем u ( e n ) = 0. C ‘равно редуцированный базис нильпотентного эндоморфизма.
Существование детерминанта. Разложение по столбцу.
Минором матрицы называется детерминант какой-либо ее квадратной подматрицы. В частности, вводится
Определение.
Пусть a_{ij} — элемент матрицы A порядка n, расположенный в i-й строке и j-м столбце. Назовем дополнительной подматрицей этого элемента матрицу D_{ij} порядка n-1, получаемую из A вычеркиванием i-й строки и j-гo столбца. Дополнительным минором элемента a_{ij} назовем число d_{ij}=\mathbf{det}\,D_{ij}.
Разумеется, говорить о дополнительном миноре имеет смысл только в том случае, если детерминант порядка n-1 существует.
Теорема 2.
На множестве квадратных матриц произвольного порядка определен детерминант.
Докажем это методом полной индукции по порядку матрицы. Начало индукции трудностей не вызывает, так как мы знаем, что известные нам детерминанты второго и третьего порядка обладают нужными свойствами.Предположим теперь, что на множестве матриц порядка n-1 детерминант существует, и построим на множестве матриц порядка n функцию следующим образом. Фиксируем произвольно номер столбца j и произвольной матрице A порядка n сопоставим число \tag{6} f_{j}(A)=\sum_{k=1}^{n} a_{kj}(-1)^{k+j} d_{kj}, где d_{kj} — дополнительный минор элемента a_{kj} в матрице A. Дополнительные миноры существуют в силу предположения индукции. Докажем, что функция удовлетворяет трем условиям, входящим в определение детерминанта.
1. Выберем произвольную строку (пусть ее номер i) и покажем, что выражение в правой части формулы есть линейный многочлен относительно элементов этой строки. В самом деле, при k=i слагаемое a_{ij}(-1)^{i+j} d_{ij} содержит элемент из i-й строки. Коэффициент при нем не зависит от элементов i-й строки, так как эта строка в подматрицу D_{ij} не входит. В остальных слагаемых (при i \neq k) множитель a_{kj} не принадлежит i-й строке, a d_{kj} — линейный многочлен от элементов i-й строки. Теперь свойство линейности по строке для функции f_{j} следует из того, что сумма линейных многочленов — линейный многочлен.
2. Докажем, что для вырожденных матриц f_{j} равна нулю. В силу и уже доказанной линейности по строке для этого достаточно проверить, что f_{j}(A)=0 для произвольной матрицы, имеющей две одинаковые строки. Пусть в матрице A строки с номерами i и l одинаковы (l > i). Тогда в сумме могут быть не равны нулю только два слагаемых, так как при k \neq i и k \neq l дополнительная подматрица D_{kj} содержит одинаковые строки, и потому минор d_{kj} равен нулю. Итак, f_{j}(A)=(-1)^{i+j}a_{ij}d_{ij}+(-1)^{l+j}a_{lj}d_{lj}.
Учтем, что a_{ij}=a_{lj} ввиду совпадения строк. Тогда \tag{7} f_{j}(A)=(-1)^{j}a_{ij}((-1)^{j}d_{ij}+(-1)^{l}d_{lj}).
Дополнительные подматрицы D_{ij} и D_{lj} состоят из одинаковых элементов, но отличаются порядком строк: в каждой из них осталась одна из двух одинаковых строк, но в D_{lj} она стоит на i-м месте, а в D_{ij} — на (l-1)-м. Переставим в матрице D_{ij} строку с номером l-1 на i-е место, не нарушая взаимное расположение остальных строк. Для этого меняем ее последовательно местами с (l-2)-й, (l-3)-й,…, i-й строками. Потребуется (l-2)-(i-1)=l-i-1 перестановок. Отсюда следует, что d_{ij}=(-1)^{l-i-1}d_{lg}. Подставив это в равенство , мы увидим, что f_{j}(A)=0.
3. Рассмотрим f_{j}(E), где E — единичная матрица порядка n. В этом случае в сумме только одно ненулевое слагаемое f_{j}(E)=(-1)^{j+j}d_{jj}.
Но D_{jj}— единичная матрица порядка n-1, и ее детерминант равен 1. Отсюда f_{j}(E)=1, как и требовалось. Теорема доказана.
В силу функции f_{j} при всех j совпадают, и мы можем написать:\tag{8} \mathbf{det}\,A=\sum_{k=1}^{n} a_{kj}(-1)^{k+j}d_{kj}.
Правая часть этой формулы — линейный многочлен от элементов j-ro столбца, следовательно, имеет место
Утверждение 7.
Детерминант обладает свойством линейности по столбцам.
мономиальный
Алгебраическое выражение, содержащее только один ненулевой член, называется мономом. Одночлен — это тип многочлена, например, биномиального и трехчленного, который представляет собой алгебраическое выражение, имеющее только один член, не равный нулю. Он состоит только из одного термина, что позволяет легко выполнять операции сложения, вычитания и умножения.
Примеры:
Различные части мономиального выражения:
- Переменная: буквы, присутствующие в выражении монома, являются переменными.
- Коэффициент : число перед переменной или число, умноженное на переменную в выражении.
- Буквенная часть: алфавиты, присутствующие вместе со значениями экспоненты, являются буквальной частью.
Рассмотрим пример 6xy 2 — мономиальное выражение,
- Коэффициент равен 6
- Переменные x и y
- Степень мономиального выражения = 1 + 2 = 3
- Буквальная часть xy 2
Мономиальная степень
Сумма значений показателей степени переменных в выражении называется степенью монома или мономиальной степенью. Если переменные не имеют значений экспоненты, их неявное значение равно 1.
Пример:
Мономиальные операции
Арифметические операции, которые выполняются над мономом, это сложение, вычитание, умножение и деление.
Сложение двух мономов:
Когда мы добавляем два одночлена с одной и той же литеральной частью, это приводит к одночленному выражению.
Пример:
Вычитание двух мономов:
Когда мы вычитаем два одночлена с одной и той же буквенной частью, это приводит к одночленному выражению.
Умножение двух мономов:
Когда мы умножаем два одночлена с одной и той же буквенной частью, это приводит к одночленному выражению.
Деление двух мономов:
Когда мы делим два одночлена с одной и той же буквенной частью, это приводит к одночленному выражению.
Создание матриц
Приведем несколько способов создания матриц в NumPy.
Самый простой способ — с помощью функции
numpy.array(list, dtype=None, …).
В качестве первого аргумента ей надо передать итерируемый объект,
элементами которого являются другие итерируемые объекты одинаковой длины
и содержащие данные одинакового типа.
Второй аргумент является опциональным и определяет тип данных матрицы.
Его можно не задавать, тогда тип данных будет определен из типа
элементов первого аргумента. При задании этого параметра будет
произведена попытка приведения типов.
Например, матрицу из списка списков целых чисел можно создать следующим
образом:
a = np.array() # Создаем одномерный массив print(type(a)) # Prints "<class 'numpy.ndarray'>" print(a.shape) # Prints "(3,)" - кортеж с размерностями print(a], a1], a2]) # Prints "1 2 3" a = 5 # Изменяем значение элемента массива print(a) # Prints "" b = np.array(,]) # Создаем двухмерный массив print(b.shape) # Prints "(2, 3)" print(b, ], b, 1], b1, ]) # Prints "1 2 4" print(np.arange(1, 5)) #Cоздает вектор с эелементами от 1 до 4
<class 'numpy.ndarray'> (3,) 1 2 3 (2, 3) 1 2 4
matrix = np.array(, 2, 5, 6], 6, 7, 4]])
print ("Матрица:\n", matrix)
Матрица: ]
Второй способ создания — с помощью встроенных функций
numpy.eye(N, M=None, …), numpy.zeros(shape, …),
numpy.ones(shape, …).
Первая функция создает единичную матрицу размера ;
если не задан, то .
Вторая и третья функции создают матрицы, состоящие целиком из нулей или
единиц соответственно. В качестве первого аргумента необходимо задать
размерность массива — кортеж целых чисел. В двумерном случае это набор
из двух чисел: количество строк и столбцов матрицы.
Примеры:
b = np.eye(5)
print ("Единичная матрица:\n", b)
Единичная матрица: ]
c = np.ones((7, 5))
print ("Матрица, состоящая из одних единиц:\n", c)
Матрица, состоящая из одних единиц: ]
d = np.full((2,2), 7) # Создает матрицу (1, 2) заполненую заданным значением
print(d) # Prints "
# ]"
e = np.random.random((2,2)) # Создает еденичную матрицу (2, 2) заполненую случаными числами (0, 1)
print(e) # Might print "
# ]"
] ]
Обратите внимание: размерность массива задается не двумя аргументами
функции, а одним — кортежем!
Вот так — np.ones(7, 5) — создать массив не получится, так как
функции в качестве параметра shape передается 7, а не кортеж
(7, 5).
И, наконец, третий способ — с помощью функции
numpy.arange(stop, , …), которая создает
одномерный массив последовательных чисел из промежутка
[start, stop) с заданным шагом step, и метода
array.reshape(shape).
Параметр shape, как и в предыдущем примере, задает размерность
матрицы (кортеж чисел). Логика работы метода ясна из следующего примера:
v = np.arange(, 24, 2)
print ("Вектор-столбец:\n", v)
Вектор-столбец:
d = v.reshape((3, 4))
print ("Матрица:\n", d)
Матрица: ]
Матричные выражения
Повторим обычные школьные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например: . При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / деление и в последнюю очередь – сложение /вычитание.
Если числовое выражение имеет смысл, то результат его вычисления является числом, например:![]()
Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.
Рассмотрим матричное выражение , где – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.
В первом слагаемом сначала нужно транспонировать матрицу «бэ»: , потом выполнить умножение и внести «двойку» в полученную матрицу
Обратите внимание, что операция транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2
Во втором слагаемом в первую очередь выполняется матричное умножение , и обратная матрица находится уже от произведения. Если скобки убрать: , то сначала необходимо найти обратную матрицу , а затем перемножить матрицы: . Нахождение обратной матрицы также имеет приоритет перед умножением.
С третьим слагаемым всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу.
Если матричное выражение имеет смысл, то результат его вычисления является матрицей.
Все задания будут из реальных контрольных работ, и мы начнём с самого простого:
Пример 9
Даны матрицы . Найти:
Решение: порядок действий очевиден, сначала выполняется умножение, затем сложение.
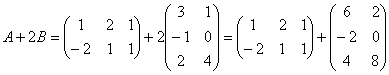
Сложение выполнить невозможно, поскольку матрицы разных размеров.
Не удивляйтесь, заведомо невозможные действия часто предлагаются в заданиях данного типа.
Пробуем вычислить второе выражение: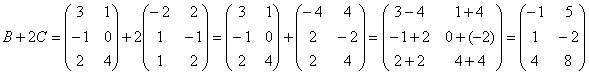
Тут всё нормально.
Ответ: действие выполнить невозможно, .
Повысим градус:
Пример 10
Даны матрицы 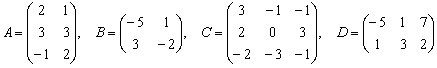 .
.
Найти значения выражений:
Решение: Разбираемся с произведением . Сначала транспонируем матрицы «дэ»:
И умножаем матрицы:
Матричное умножение выполнить невозможно, так как число столбцов матрицы не равно числу строк матрицы .
А вот с произведением проблем не возникает: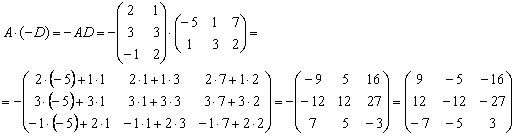
Еще раз заметьте, как на первом же шаге множитель (–1) выносится вперёд, и ноги до него доходят в самую последнюю очередь.
С более сложными выражениями вроде чайникам рекомендую разбираться поэтапно, чтобы не запутаться:
Сначала находим произведение: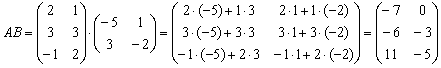
Затем считаем второе слагаемое:
И, наконец, всё выражение: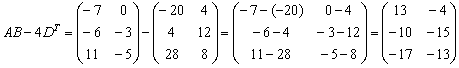
Более подготовленные студенты могут оформить решение одной строкой: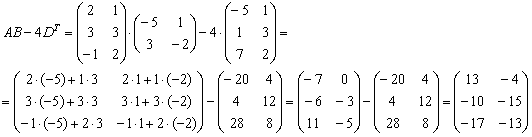
Ответ: действие выполнить невозможно, , .
Пара заключительных примеров для самостоятельного решения:
Пример 11
Для матриц Примера №10 выполнить действия:
Пример 12
Вычислить значение матричного многочлена , если .
В последнем примере решение удобно оформить по пунктам.
Матричные выражения – это просто! И вряд ли на практике вам встретится что-то сложнее, чем разобранные примеры.
Теперь во всеоружии можно приступить к изучению матричных уравнений.
Желаю успехов!
Решения и ответы:
Пример 2: Решение: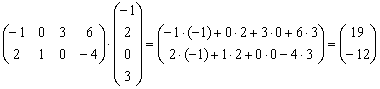 Ответ
Ответ
Пример 5: Решение: ![]() Ответ
Ответ
Пример 7: Решение: 1) Используем формулу  2) Используем формулу
2) Используем формулу  Ответ
Ответ
Пример 8: Решение: Сначала возведём матрицу в квадрат:![]() Возведём матрицу в куб:
Возведём матрицу в куб:![]() Возведём матрицу в четвёртую степень двумя способами:
Возведём матрицу в четвёртую степень двумя способами:![]()
![]() Ответ
Ответ
Пример 11: Решение:![]()
Возведение в квадрат невозможно, поскольку операция определена только для квадратных матриц.
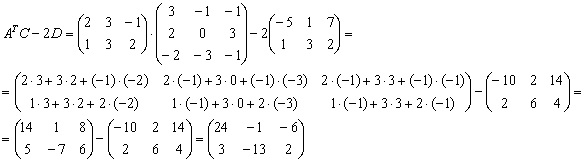
Ответ: , действие выполнить невозможно,
Пример 12: Решение: 1) ![]() 2) 3)
2) 3) ![]() 4) 5)
4) 5) ![]() ОтветПримечание: выражение можно было вычислить и по-другому – предварительно раскрыть скобки:
ОтветПримечание: выражение можно было вычислить и по-другому – предварительно раскрыть скобки:
(Переход на главную страницу)
Ну и что
Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют.
Текст:
Александр Бабаскин
Редактура:
Максим Ильяхов
Художник:
Даня Берковский
Корректор:
Ирина Михеева
Вёрстка:
Мария Дронова
Соцсети:
Олег Вешкурцев
Математические операции
К массивам (матрицам) можно применять известные вам математические
операции. Следут понимать, что при этом у элементов должны быть схожие
размерности. Поведение в случае не совпадения размерностей хорошо
описанно в документации numpy.
x = np.array(,], dtype=np.float64) y = np.array(,], dtype=np.float64) arr = np.array()
# Сложение происходит поэлеметно
#
# ]
print(x + y)
print()
print(np.add(x, y))
print('С числом')
print(x + 1)
print('C массивом другой размерности')
print(x + arr)
] ] С числом ] C массивом другой размерности ]
# Вычитание print(x - y) print(np.subtract(x, y))
] ]
# Деление # # ] print(x y) print(np.divide(x, y))
] ]
# Другие функции # # ] print(np.sqrt(x))
Многочлены от матриц
Напомним определение многочлена от матрицы. Пусть заданы многочлен (степени ) переменной
(7.40)
где — квадратная матрица n-го порядка. Выражение вида
(7.41)
называется многочленом от матрицы .
При больших значениях и вычисление выражения (7.41) затруднительно из-за операции возведения матрицы в натуральную степень. Поэтому требуется найти другие, эквивалентные определению (7.41), формы записи и алгоритмы эффективного вычисления многочлена от матрицы. Для упрощения (7.41) имеются две возможности. Во-первых, можно упростить матрицу так, чтобы многочлен (7.40) от упрощенной матрицы уже вычислялся сравнительно просто. Например, выражение (7.41) легко вычисляется, если матрица диагональная. Во-вторых, можно понизить степень многочлена, тогда самая трудоемкая операция — возведение матрицы в степень — упрощается.
Как найти f(a) при помощи спектрального разложения матрицы?
Спектральное разложение матрицы – это представление матрицы в виде суммы ее собственных значений и ее собственных векторов. При наличии спектрального разложения матрицы a, матричный многочлен f(a) можно найти следующим образом:
- Разложить матрицу a в собственные векторы и собственные значения (можно воспользоваться методом Гаусса или Жордана).
- Подставить собственные значения в матричный многочлен f(x) и сформировать новый матричный многочлен f(λ), где λ – собственное значение.
- Для каждого собственного значения λ найти соответствующий ему собственный вектор.
- Собрать полученные матрицы в линейную комбинацию f(λ) и собственных векторов.
- Полученную матрицу можно сократить, если некоторые собственные значения повторяются.
Найденный результат будет представлять собой матрицу, которая и является значением матричного многочлена f(a).
К примеру, пусть задана матрица:
| a | −1 | 2 |
| 3 | 4 | 5 |
| 1 | 2 | −3 |
Для нахождения значения матричного многочлена f(a) при условии f(x) = x^2 − 4x + 1, нужно:
- Найти собственные значения матрицы a: λ1 = -1, λ2 = 2, λ3 = 2.
- Рассчитать соответствующие собственные векторы:
| λ1=-1 | V1 | | | −1 | 2 | |
| | | 3 | 4 | 5 | ||
| | | 1 | 2 | 2 | ||
| λ2=2 | V2 | | | −1 | 2 | |
| | | 3 | 4 | 5 | ||
| | | 1 | 2 | 5 | ||
| λ3=2 | V3 | | | −1 | 2 | |
| | | 3 | 4 | 5 | ||
| | | 1 | 2 | 1 |
Подставить собственные значения в матричный многочлен f(x) и сформировать новый матричный многочлен f(λ):
| λ | f(λ) |
| -1 | 6 |
| 2 | -3 |
| 2 | -3 |
Собрать полученные матрицы в линейную комбинацию f(λ) и собственных векторов:
| V | f(λ) | f(a) | ||
| −1 | 1 | 6 | + | -2 |
| 2 | -1 | -3 | + | 5 |
| 1 | -3 | + | -10 |
Полученная матрица — результат матричного многочлена f(a).



























