Нахождение длины периода
Определение длины периода функции является важной задачей в анализе и вычислительной математике. Длина периода функции определяет, через какие интервалы функция повторяется
В данной статье мы рассмотрим шаги для определения длины периода функции.
- Понять понятие периода. Период функции — это наименьшая положительная константа T, для которой выполняется условие f(t+T) = f(t) для всех значений t, где f — функция, определенная на интервале.
- Найти первый интервал, где функция повторяется. Начните поиск, начиная с самого маленького положительного значения T. Найдите такое T, при котором выполняется условие f(t+T) = f(t).
- Тестирование других интервалов. Проверьте, повторяется ли функция на других интервалах с длиной T. Если да, то это будет подтверждение длины периода.
- Найти кратчайший период. Если функция повторяется на нескольких интервалах, найдите самый короткий из них — это и будет длина периода функции.
- Учесть особенности функции. Некоторые функции могут иметь особые свойства, связанные с периодичностью. Например, функция синуса имеет период 2π.
- Воспользуйтесь вычислительными методами. Если функция сложная и не поддается аналитическому решению, можно воспользоваться численными методами для нахождения периода.
Надеюсь, эти шаги помогут вам определить длину периода функции быстро и эффективно. Пользуйтесь этой информацией в аналитических и вычислительных задачах, где знание периода функции может быть важным фактором.
Свойства периодических функций
Периодические функции обладают рядом уникальных свойств, которые делают их особенными и полезными в математике и физике.
1. Сдвиг периодической функции
Если функция f(x) является периодической с периодом T, то сдвиг функции на целое число периодов T также будет периодической функцией с периодом T. Например, если f(x) = sin(x) — периодическая функция с периодом 2π, то f(x + T) = sin(x + T) также будет периодической функцией с периодом 2π.
2. Сложение периодических функций
Если функции f(x) и g(x) являются периодическими с одинаковыми периодами T, то их сумма h(x) = f(x) + g(x) также будет периодической функцией с периодом T. Например, если f(x) = sin(x) и g(x) = cos(x) — периодические функции с периодом 2π, то h(x) = sin(x) + cos(x) также будет периодической функцией с периодом 2π.
3. Умножение периодической функции на константу
Если функция f(x) является периодической с периодом T и c — константа, то произведение h(x) = c * f(x) также будет периодической функцией с периодом T. Например, если f(x) = sin(x) — периодическая функция с периодом 2π, и c = 2, то h(x) = 2 * sin(x) также будет периодической функцией с периодом 2π.
Перечисленные свойства позволяют использовать периодические функции для анализа и решения различных задач в математике и физике. Они облегчают вычисления и позволяют упростить математические модели, а также понять и объяснить различные явления и закономерности.
Периодические функции и сдвиг
Сдвиг функции — это изменение ее аргумента при сохранении значения функции. Другими словами, сдвиг функции приводит к смещению ее графика на оси аргументов без изменения его формы.
В случае периодических функций, сохраняя периодичность, можно осуществить сдвиг на целое число периодов. Например, если у нас есть периодическая функция f(x) с периодом T, то ее сдвиг на T приведет к получению функции f(x-T), которая будет иметь такую же форму как и исходная функция f(x), но будет расположена на оси аргументов вдоль направления отрицательной полуоси.
Аналогично, сдвиг на 2T приведет к функции с аргументом f(x-2T), которая будет расположена по отрицательной полуоси на два периода от исходной функции f(x). Таким образом, сдвиг на любое целое число периодов T приведет к получению совершенно эквивалентной периодической функции.
Сдвиг периодической функции имеет большое практическое значение в решении различных задач. Он позволяет приводить задачи к более удобному и простому виду, упрощая расчеты и приводя к более наглядному представлению решения.
Также стоит отметить, что сдвиг периодической функции может быть как по положительной, так и по отрицательной полуоси оси аргументов. При этом, сдвиг на отрицательное число периодов эквивалентен сдвигу на положительное число периодов с изменением направления смещения.
Таким образом, сдвиг является одним из фундаментальных свойств периодических функций, которое широко применяется в различных областях науки и техники.
Сложение и умножение периодических функций
При сложении периодических функций, мы складываем значения функций в каждой точке. Таким образом, если у нас есть две периодические функции f(x) и g(x) с одинаковым периодом Т, то сумма этих функций h(x) = f(x) + g(x) также будет периодической функцией с периодом Т.
Умножение периодических функций подобно сложению. Мы перемножаем значения функций в каждой точке. Если у нас есть две периодические функции f(x) и g(x) с периодом Т, то произведение этих функций h(x) = f(x) * g(x) также будет периодической функцией с периодом Т.
Комбинируя сложение и умножение, мы можем создавать бесконечное количество новых периодических функций. Например, мы можем умножить периодическую функцию f(x) на постоянное число a, чтобы получить новую периодическую функцию h(x) = a * f(x). Мы также можем сложить несколько периодических функций, чтобы получить новую функцию.
Сложение и умножение периодических функций играют важную роль в математике и физике. Эти операции позволяют нам моделировать и представлять различные периодические явления и процессы, такие как колебания, волны, электромагнитные поля и многое другое. Они также позволяют нам анализировать и решать уравнения, связанные с периодическими функциями.
Таким образом, сложение и умножение периодических функций предоставляют нам мощный инструмент для работы с периодическими явлениями и процессами, а также для создания новых функций и моделей в математике и физике.
Видео:Функции. Урок №6. Периодичность функции.Скачать

Феномен периодичности
Феномен периодичности широко распространен в природе. Например, сезоны года, деление суток на день и ночь, фазы Луны, пульсация звезд и циклы жизни организмов – все это примеры проявления периодичности.
Периодичность также наблюдается в физике, химии и математике. Волновые процессы, колебания, смена электрических зарядов, а также функции и графики с периодическими характеристиками – все это связано с периодичностью.
Феномен периодичности играет важную роль в изучении различных явлений, позволяет прогнозировать тренды и поведение систем. Математическое описание периодических функций и процессов позволяет установить закономерности и применить их в практических задачах.
В итоге, феномен периодичности – это фундаментальное свойство многих явлений и процессов, которое помогает понять и объяснить повторяемость и систематичность мира вокруг нас.
Причины периодичности
Причины периодичности можно объяснить различными факторами. Одной из причин является наличие стабильных и повторяющихся условий или факторов, которые влияют на возникновение и характер явления. Например, изменение времени суток может привести к периодичности в поведении животных или циклам растений.
Также периодичность может быть обусловлена внешними воздействиями, такими как изменение времен года, цикличность приливов и отливов, солнечной активности и других природных процессов. Эти воздействия создают определенные условия, которые приводят к повторению определенных явлений и процессов через определенные промежутки времени.
Важное значение в появлении периодичности имеет также внутренняя организация систем и процессов. Некоторые явления имеют структуру, которая сама по себе обладает периодическими характеристиками
Например, колебания в физических системах, таких как маятники или электрические цепи, обусловлены внутренней структурой системы и их периодичность является следствием взаимодействия составляющих их элементов.
Кроме того, периодичность может быть связана с внутренними процессами и циклами, которые происходят внутри организмов или систем. Например, в биологии существует множество физиологических процессов, таких как суточные ритмы человека или менструальный цикл у женщин, которые происходят с определенной периодичностью.
Все эти причины периодичности объясняют появление и регулярность повторения различных явлений и процессов в природе и обществе. Изучение периодичности позволяет понять закономерности и принципы, которые лежат в основе различных явлений и процессов и применить их в практических целях.
Значение периодичности в природе
Периодичность может быть обнаружена в различных сферах природы. Один из известных примеров – это смена времен года. Каждый год мы можем наблюдать повторяющийся цикл изменения погоды – зима, весна, лето и осень. Это связано с периодическими изменениями в солнечной активности и географическом положении Земли. Знание этого цикла позволяет нам адаптироваться к изменению условий и принимать необходимые меры для сохранения комфорта и безопасности.
Другой пример периодичности в природе – это популяции животных и растений. Многие виды имеют свои циклы размножения и миграций. Наблюдение за этими периодами позволяет нам понять и прогнозировать изменения в экосистеме и принимать меры для ее сохранения.
Периодичность также является важным аспектом в изучении климатических изменений и геологических процессов. Измерение периодичности землетрясений, вулканической активности, паводков и других природных катастроф позволяет улучшить системы предупреждения и максимально снизить потенциальный ущерб.
Таким образом, периодичность процессов и явлений в природе имеет огромное значение для нашего понимания и взаимодействия с окружающей средой. Она помогает нам предсказывать и адаптироваться к изменениям, защищать и сохранять разнообразие жизни на Земле, а также предотвращать и минимизировать возможные угрозы для человечества и природы в целом.
Периодичность в физике: влияние сил и механизмы
Периодичность в физике обусловлена взаимодействием различных сил, которые действуют на систему. Наиболее известная периодичность в механике — это периодичность колебаний. Она проявляется, например, при колебаниях маятника или пружинного маятника.
Колебания обусловлены действием упругой силы, которая стремится вернуть систему в равновесное положение. Эта сила действует против силы инерции, которая характеризует сопротивление изменению скорости тела. В результате взаимодействия этих сил возникает периодическое движение системы.
Однако периодичность может проявляться и в других видах сил. Например, в электромагнетизме периодичные процессы связаны с колебаниями электромагнитных волн, которые передают энергию и информацию. Здесь периодичность обусловлена взаимодействием между электрическими и магнитными силами.
Периодичность в атомной физике связана с энергетическими уровнями атомов и колебаниями электронов вокруг ядра. В данном случае взаимодействие осуществляется за счет электромагнитных сил и квантовых свойств атомных систем.
Итак, периодичность в физике зависит от типа взаимодействия сил и механизмов, которые описывают данные процессы. Различные силы действуют на систему с разной силой и направлением, чтобы вызвать периодическое поведение. Понимание периодичности в различных областях физики позволяет предсказывать поведение систем и разрабатывать новые технологии и устройства.
Примеры
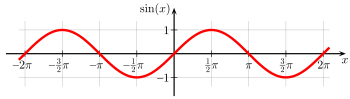
График синусоидальной функции, показывающий два полных периода
Примеры реальных чисел
Синусоидальная функция является периодической с периодом , так
2π{\ displaystyle 2 \ pi}
- грех(Икс+2π)знак равногрехИкс{\ Displaystyle \ грех (х + 2 \ пи) = \ грех х}
для всех значений . Эта функция повторяется с интервалами длины (см. График справа).
Икс{\ displaystyle x}2π{\ displaystyle 2 \ pi}
Когда переменная — время, можно увидеть повседневные примеры ; например, стрелки часов или фазы луны показывают периодическое поведение. Периодическое движение — это движение, при котором положение (я) системы выражается в виде периодических функций с одним и тем же периодом.
Для функции от действительных чисел или от целых чисел это означает, что весь граф может быть сформирован из копий одной конкретной части, повторяющихся через равные промежутки времени.
Простым примером периодической функции является функция, которая дает « дробную часть » своего аргумента. Его период равен 1. В частности,
ж{\ displaystyle f}
- ж(0,5)знак равнож(1.5)знак равнож(2,5)знак равно⋯знак равно0,5{\ Displaystyle f (0,5) = f (1,5) = f (2,5) = \ cdots = 0,5}
График функции — это пилообразная волна .
ж{\ displaystyle f}
Сюжет и ; обе функции периодичны с периодом 2π.ж(Икс)знак равногрех(Икс){\ Displaystyle е (х) = \ грех (х)}грамм(Икс)знак равнопотому что(Икс){\ Displaystyle г (х) = \ соз (х)}
Тригонометрические функции синус и косинус являются общими периодическими функциями с периодом 2л (см рисунок справа). Предмет ряда Фурье исследует идею о том, что «произвольная» периодическая функция является суммой тригонометрических функций с совпадающими периодами.
Согласно приведенному выше определению, некоторые экзотические функции, например, функция Дирихле , также являются периодическими; в случае функции Дирихле любое ненулевое рациональное число является периодом.
Примеры комплексных чисел
Используя комплексные переменные, мы получаем функцию общего периода:
- еяkИксзнак равнопотому чтоkИкс+ягрехkИкс.{\ displaystyle e ^ {ikx} = \ cos kx + i \, \ sin kx.}
Поскольку обе функции косинуса и синуса являются периодическими с периодом 2π, комплексная экспонента состоит из косинусных и синусоидальных волн. Это означает, что формула Эйлера (см. Выше) обладает таким свойством, что если L — период функции, то
- Lзнак равно2πk.{\ displaystyle L = {\ frac {2 \ pi} {k}}.}
Двойные периодические функции
Функция, областью определения которой являются комплексные числа, может иметь два несоизмеримых периода, не будучи постоянной. В эллиптических функциях такие функции. («Несоизмеримые» в этом контексте означает, что они не могут быть кратными друг другу.)
Определение периодичности
Периодичность функции — это повторение определенного паттерна в ее значениях через заданный интервал. Определить периодичность функции можно с помощью следующих шагов:
- Изучение графика функции. На графике можно обнаружить повторяющиеся участки и сделать предположение о периодичности функции.
- Расчет разности между значениями функции для разных аргументов. Если разность между значениями равна определенному числу, это может указывать на периодичность функции.
- Проверка функции на равенство значений при смещении аргумента на определенное число (период). Если функция возвращается к начальному значению, то это может указывать на периодичность.
- Исследование функции на симметричность относительно оси абсцисс. Если функция симметрична, то она, скорее всего, периодична.
- Построение таблицы значений функции для разных аргументов и поиск повторяющихся значений. Если значения функции повторяются через заданный интервал, это может указывать на периодичность.
- Расчет производной функции и анализ ее свойств. Если производная функции имеет периодическую структуру, то и сама функция, скорее всего, периодична.
Если один или несколько шагов указывают на возможную периодичность функции, следует провести более детальный анализ, чтобы подтвердить или опровергнуть это предположение.
Факторы социальной периодичности
Факторы, влияющие на социальную периодичность, могут быть разнообразными и зависеть от конкретной области исследования. Рассмотрим некоторые основные факторы:
- Сезонность — это регулярность явлений, связанная с сезонными изменениями. В разных областях социальной деятельности можно наблюдать сезонные колебания: уровень преступности, уровень заболеваемости, покупательская активность и т. д.
- Дневная периодичность — это регулярность явлений, связанная с циклом суток. Во многих случаях между ночной и дневной активностью людей можно обнаружить определенные закономерности: время работы, время отдыха, суточные ритмы питания и т. д.
- Недельная периодичность — это регулярность явлений, связанная с циклом недели. Некоторые социальные процессы, например, уровень зарплат, праздники, изменение трафика в городах, могут иметь недельные циклы.
- Годовая периодичность — это регулярность явлений, связанная с циклом года. Конечно, наиболее очевидным примером является смена сезонов, но также есть и другие факторы, влияющие на социальную периодичность в течение года: праздники, начало учебного года, сезонные спортивные соревнования.
Это лишь некоторые из факторов, влияющих на социальную периодичность, и список может быть значительно дополнен в зависимости от конкретных исследований и областей интереса. Изучение социальных периодичностей позволяет выявлять закономерности и прогнозировать различные социальные явления, что может быть полезно для планирования и принятия решений в различных областях жизни общества.
Связь с природными явлениями
Периодичность явления может быть связана с различными природными факторами. Вот некоторые из них:
| Природное явление | Факторы периодичности |
|---|---|
| Приливы и отливы | Влияние луны и солнца на гравитационные силы |
| Смена дня и ночи | Вращение Земли вокруг своей оси |
| Смена времен года | Наклонность оси Земли в отношении солнечных лучей |
| Солнечные затмения | Периоды, в которые Луна находится в определенном положении относительно Земли и Солнца |
Это только некоторые примеры того, как периодичность различных природных явлений может быть связана с различными факторами. Многое еще нужно изучить для полного понимания этой темы.
Что такое периодичность в математике?
Периодичность в математике – это свойство некоторых функций или последовательностей возвращаться к одним и тем же значениям с определенной периодичностью. Периодическая функция или последовательность повторяет свои значения через определенные интервалы, называемые периодом.
Периодичность встречается во многих важных математических концепциях и является основой для многих прикладных наук. Она имеет различные применения в физике, химии, инженерии и других областях.
Для функции, чтобы быть периодической, существует такое число T, называемое периодом функции, что для каждого значения x выполняется равенство f(x) = f(x + T). То есть, если мы сдвигаем аргумент функции на значение периода, значение самой функции не изменится.
Существует два вида периодичности – периодичность в дискретной математике и периодичность в непрерывной математике. Периодичность в дискретной математике связана с последовательностями, в то время как периодичность в непрерывной математике связана с функциями.
Периодическая последовательность может быть представлена в виде таблицы или графика. В таблице значения последовательности периодически повторяются через определенные интервалы. В графической форме периодическая последовательность будет иметь форму графика, который повторяется через определенные интервалы.
Периодичность в математике имеет множество приложений. Например, периодичность используется для представления повторяющихся сигналов или колебаний в физике. Она также применяется в теории вероятностей и статистике, где периодичность помогает предсказывать повторяемые события.
Сущность периодичности в математике
В математике периодическая функция — это функция, которая повторяется с определенным интервалом, который называется периодом. То есть, если для функции f(x) существует такое число T, что f(x + T) = f(x) для всех значений x, то эта функция является периодической.
Примером периодической функции может служить синусоида (sin(x)) или косинусоида (cos(x)), которые повторяются через один период, равный 2π.
Одной из основных особенностей периодических функций является их свойство сохранять форму и значения при сдвиге на один или несколько периодов. Это означает, что если для функции f(x) существует период T, то f(x + T) = f(x), f(x + 2T) = f(x) и т. д.
Также периодические функции обладают свойствами сложения и умножения. А именно, сумма или разность двух периодических функций является периодической функцией с тем же периодом, а произведение периодической функции на постоянное число также является периодической функцией с тем же периодом.
Периодические функции имеют различные применения в математике и физике. Например, они используются для описания колебаний, звуковых волн, электромагнитных полей и других физических явлений. Также периодические функции используются в анализе временных рядов, сигналов и данных.
Определение периодической функции
В математике периодической функцией называется функция, которая обладает таким свойством, что для каждого значения аргумента существует такое число, называемое периодом функции, при котором значение функции повторяется.
Формально можно сказать, что функция f(x) называется периодической, если существует такое положительное число T, что для любого значения x выполняется равенство:
| f(x + T) = f(x) |
|---|
Здесь T представляет собой период функции f(x).
Периодические функции встречаются во многих областях математики и физики. Примерами периодических функций можно назвать синусоиду, косинусоиду и параболу. Они имеют хорошо определенные периоды и повторяются с определенными промежутками.
Определение периодической функции позволяет нам более удобно изучать поведение функции на всем протяжении ее области определения, так как зная значение функции на одном периоде, мы можем легко вычислить значение на другом периоде.
Важно отметить, что периодические функции имеют много интересных свойств, которые можно использовать в математике и физике для решения различных задач. Изучение периодических функций оказывает огромную практическую значимость и находит применение в различных областях науки
Примеры периодических функций
- Синусоидальная функция: одним из наиболее известных примеров периодической функции является синусоида. Синусоидальная функция повторяет свое значение при изменении аргумента на 2пи. Она широко используется при описании колебаний и волн, а также в физике и инженерии.
- Ступенчатая функция: это функция, которая принимает константные значения на интервалах, разделенных точками скачка. Например, функция Хевисайда, которая равна 0 для отрицательных аргументов и 1 для положительных аргументов.
- Пилообразная функция: данная функция представляет собой линейную функцию с периодической изменяющимся наклоном. Например, функция пилообразной формы может иметь период 2 и наклон 1, то есть она будет повторяться с шагом 2 и иметь наклон равный 1.
- Модульная функция: это функция, которая равна модулю аргумента. Например, функция модуля |x| будет иметь период 2, так как она повторяется при изменении аргумента на 2.
- Экспоненциальная функция: экспоненциальная функция также может быть периодической, если ее аргумент является комплексным числом. Например, функция e^ix будет периодической с периодом 2пи.
Это лишь некоторые примеры периодических функций, которые активно применяются в математике, физике, инженерии и других науках. Знание и понимание этих функций позволяет решать различные задачи и моделировать разнообразные явления.
Видео:Периодичность функции. Определение периодической функции. Свойства функции. Алгебра 7-11 класс.Скачать

Влияние культурных особенностей
При определении периодичности то и от чего она зависит, важно также учесть культурные особенности общества. Культура каждой страны или региона имеет свои уникальные традиции, обычаи и ценности, которые могут оказывать влияние на периодичность и ее факторы
К примеру, в некоторых культурах существует четкое разделение времени на рабочую и отдыховую части дня. Это может повлиять на периодичность, так как люди в этих культурах могут иметь привычку выполнять определенные действия в определенное время, например, обедать в 12:00 или проводить домашние хлопоты в конкретные дни недели. Такие культурные особенности могут создавать определенные ритмы и паттерны в жизни людей, которые могут отображаться в периодичности.
Культурные особенности могут также влиять на выбор меры периодичности. Например, в западных культурах широко используется седмичная периодичность, так как в них выделяется один выходной день в неделю. В отличие от этого, в некоторых азиатских культурах более популярной может быть установка месячной или годовой периодичности, связанной с особыми праздниками и традициями.
Таким образом, для определения периодичности и ее факторов важно учесть не только биологические и социально-экономические аспекты, но и культурные особенности общества. Культура может создавать свои уникальные ритмы и паттерны, которые отображаются в периодичности и способе ее измерения
Понятие периодической функции.
ГЛАВНАЯ » Материалы для обучения
периодическая функция
основной период
Тригонометрические функции обладают свойством периодичности, которое определяется в общей форме следующим образом.Определение. Функция $f(x)$ называется периодической с периодом $T$ ($T \neq 0)$, если для любого $x$ выполнено условие: если функция определена в одной из точек $x$ или $x + T$, то она определена и во второй точке, и ее значения в обеих точках равны между собой:
$f(x) = f(x + T)$. (1)Число $T$ называется в этом случае периодом функции $f(x)$. Докажем следующее предложение:
Если $T$ — период функции $f(x)$, то и любое из чисел $nT, n = — 1, \pm 2, \cdots$, также является периодом $f(x)$.
Доказательство. Проведем сначала доказательство для $-T$. Для этого рассмотрим пару значений аргумента $x$ и $x + (-T) = x — T$. Из записи
$x = (x — T) + T$
видно (в силу определения периодичности), что если функция определена в одной из точек $x-T, x$, то она определена и во второй точке. Далее устанавливаем равенство $f(x-T) = f(x)$:
$f(x) = f((x-T) + T) = f(x-T)$.
Доказательство того, что $nT$ при натуральном $n$ является периодом функции $f(x)$, проведем по индукции (случай отрицательного $n$ сводится к этому заменой $T$ на $-T$). Итак, требуется установить, что если $f(x)$ определена в одной из точек $x, x + nT$, то она определена и во второй точке, причем $f(x) = f(x+nT)$. Допустим, что утверждение теоремы уже доказано для некоторого $n = k$ (оно, например, очевидно при $n = 1$). Докажем, что оно останется верным и для $n = k + 1$. Прежде всего, в силу того, что $T$ — период, замечаем, что если одно из значении аргумента $x+kT$ и $x+(k+1) T = (x+kT) + T$ принадлежит области определения функции, то ей принадлежит и второе значение. Так как, по предположению индукции, такое же положение справедливо и для пары точек $x$ и $x + kT$, то видно, что точки $x$ и $x + (k+1)T$ принадлежат (или не принадлежат) области определения $f(x)$ одновременно. Далее устанавливаем равенство значений $f(x)$ в точках $x$ и $x +(k+1)T$:
$f(x + (k+1)T) = f(x + kT + T) = f(x + kT) = f(x)$ (последнее — по предположению индукции).
Доказано, что $nT$ — период функции при любом целом $n$. Наименьший положительный период функции (если он существует) называется основным периодом.
Пример 1. Функция $f(x) = c$ ($c$ — постоянная величина) имеет своим периодом любое число. Основного периода здесь нет. График этой функции изображен на рис.
Пример 2. Напомним, что целой частью числа $x$ (обозначение: $$) называется наибольшее целое число, не превосходящее $x$. Целая часть х есть функция от $x$; ее график показан на рис.
Дробной частью числа $x$ (обозначение: $(x)$) мы назвали разность между $x$ и его целой частью:
$(x) = x — $.
Дробная часть $x$ является периодической функцией с основным периодом $T = 1$. Действительно,
$(x + 1) = x + 1 — $,
и так как очевидно, что $ = = + 1$, то
$(x + 1) = x + 1 — = x + 1 — — 1 = x — = (x)$.
График дробной части $x$ показан рис.
Пример 3. а) Рассмотрим следующую функцию $f(x)$, определенную для $x$, удовлетворяющих неравенствам $0 \leq x
$f(x) = \begin{cases} x \: при \: 0 \leq
График функции изображен на рис.
б) С помощью этой функции $f(x)$, приняв за основной период число $T = 2$, построим периодическую функцию $F(x)$:
$F(x) = \begin{cases} x — \: при \: 2n \leq x
$n = 0, \pm 1, \pm 2, \cdots$
График функции $F(x)$ изображен на рис.
Периодичность в культуре и искусстве: потребности и вдохновение
Периодичность организует время и пространство, обеспечивая структуру и порядок. Многие формы искусства, такие как музыка, танец, драма и кино, строятся на основе ритмических элементов и повторяющихся структур. Эта периодичность создает ощущение гармонии и удовлетворяет наши потребности в предсказуемости и порядке.
Искусство также ищет вдохновение в природных циклах и сезонах. Великие художники, поэты и музыканты на протяжении веков вдохновлялись меняющимися временами года, растущими и умирающими цветами, циклами жизни и смерти. Эта периодичность придает искусству глубину и символическую значимость, позволяя нам увидеть обширные темы и идеи, утонченные гармонии и противопоставления.
| Периодичность в культуре и искусстве: | Примеры |
|---|---|
| Музыка | Музыкальная композиция, состоящая из повторяющихся мотивов и ритмических секций. |
| Танец | Хореография, основанная на ритме и повторяемых движениях. |
| Литература | Повествование, строенное на сочетании повторяющихся структур и мотивов. |
| Живопись | Использование цикличности и повторения в композиции и мотивах произведения. |
Периодичность в культуре и искусстве является инструментом для создания гармонии, порядка и символического значения. Она удовлетворяет наши потребности в ритме и повторении, позволяет нам увидеть красоту и глубину созданных человеком произведений, а также вдохновляет нас и помогает нам понять наше место в мире.
Что такое периодичность?
Одним из основных примеров периодичности является годовой цикл природных сезонов. В течение года повторяются зима, весна, лето и осень, при этом каждый сезон длится примерно одинаковое количество времени. Это позволяет нам ожидать появления определенных признаков и изменений в окружающей среде каждый год.
| Область | Примеры периодичности |
|---|---|
| Физика | Период колебаний маятника, электромагнитные волны |
| Химия | Периодическая таблица химических элементов, химические реакции |
| Астрономия | Периодическое движение планет, лунных фаз |
| Биология | Циклы сна и бодрствования, менструальный цикл |
Периодичность имеет большое значение для проведения научных исследований и прогнозирования будущих событий. Например, на основе знания периодичности погодных изменений мы можем предсказывать сезонные стихийные бедствия или разрабатывать планы посева и уборки сельскохозяйственных культур.
В итоге, понимание и изучение периодичности позволяет нам открывать и объяснять законы природы, предсказывать события и разрабатывать эффективные стратегии в различных областях науки и жизни.
Определение периодичности
Периодичность может проявляться в различных аспектах. Например, в физике периодичность может быть связана с колебаниями, в химии — с периодическими закономерностями в таблице Менделеева, а в биологии — с ежемесячным циклом женского организма.
Определить периодичность можно с помощью различных методов и инструментов, в зависимости от конкретного процесса или явления. Например, в физике для измерения периодичности колебаний могут использоваться осциллографы или простые счетчики времени. Астрономы могут наблюдать периодичное движение планет и звезд с помощью телескопов и специальных программ для анализа данных.
Определение периодичности имеет важное практическое значение. Знание о периодичности процессов и явлений позволяет предсказывать их повторение и прогнозировать будущие события
Например, на основе периодичности солнечных затмений астрономы могут составить точное расписание этих явлений на несколько лет вперед.
| Область науки | Пример периодичности |
|---|---|
| Физика | Период колебаний маятника |
| Химия | Периодическая таблица элементов |
| Биология | Ежемесячный цикл женского организма |
| Астрономия | Периодичность солнечных затмений |
Таким образом, периодичность — это важный феномен, который широко применяется в научных исследованиях и имеет практическое значение для прогнозирования и понимания различных процессов и явлений.
Примеры периодических процессов и явлений
1. Отношения между днем и ночью — природные явления, которые изменяются с определенной периодичностью в 24 часа.
2. Пульсация сердца — периодическое сокращение и расслабление сердечной мышцы, которое происходит с определенной регулярностью.
3. Приливы и отливы — ежедневные изменения уровня моря, вызванные гравитационным взаимодействием Земли и Луны.
4. Колебания маятника — периодическое движение маятника вокруг своей оси, которое зависит от его длины и массы.
5. Смена времен года — повторение четырех сезонов — весны, лета, осени и зимы — с определенной периодичностью в году.
6. Электрический ток в переменном токе (AC) — ток, который меняется в направлении и силе с определенной периодичностью.
Эти и другие примеры демонстрируют, как периодичность процессов и явлений может быть наблюдаема в разных областях нашей жизни и научных дисциплинах.





























