Удвоенный квадрат

Введение

Заметка затрагивает тему кватернионов в срезе компьютерной графики в трехмерных приложений.

Кватернионы — это система гиперкомплексных чисел, образующая векторное пространство, которая может быть использована как способ описания вращения объекта в пространстве вокруг произвольной оси в пространстве. Открыты в 1843 г. У.Р. Гамильтоном. Подробнее данное определение будет раскрыто по пути рассмотрения связанной теории.

Под гиперкомплексными числами следует понимать обобщение понятия о числе, более широкое, чем обычные комплексные числа. Смысл обобщения состоит в том, чтобы обычные арифметические действия над такими числами одновременно выражали некоторые геометрические процессы в многомерном пространстве или давали количественное описание каких-либо физических законов.

Важное замечание: зачастую гиперкомплексные числа приравнивают к комплексным, но автор считает это не корректным. Тема является весьма глубокой и для её понимания требуются базовые знания о матрицах, множествах и конкретно о комплексных числах, группах и телах. Автор постарается раскрыть большую часть определений, но при этом не создать бесконечную заметку

Часть теории здесь может быть не обязательной, но полезной для некоторых читателей для понимания математической картины, частью которой являются кватернионы

Автор постарается раскрыть большую часть определений, но при этом не создать бесконечную заметку. Часть теории здесь может быть не обязательной, но полезной для некоторых читателей для понимания математической картины, частью которой являются кватернионы

Тема является весьма глубокой и для её понимания требуются базовые знания о матрицах, множествах и конкретно о комплексных числах, группах и телах. Автор постарается раскрыть большую часть определений, но при этом не создать бесконечную заметку. Часть теории здесь может быть не обязательной, но полезной для некоторых читателей для понимания математической картины, частью которой являются кватернионы.

Содержание заметки:

• ;
• • ,
  • ,
  • ,
  • ,
  • ,
  • ,
  • ;
• ;
• :
  • ,
  • ,
  • ;
  • .

Методы структурирования информации

Процесс изучения человеческого мозга не проходит зря. Ученые вывели несколько методик и способов структурирования информации, которые позволяют сделать запоминание намного более удобным. Мы поговорим об основных и самых популярных способах.

Метод римской комнаты, или цепочка Цицерона, — это очень простой, но эффективный метод для усвоения материала. Он заключается в том, что запоминаемые объекты необходимо мысленно расставить в вашей комнате или той, которую вы очень хорошо знаете. Главное условие в том, что все предметы должны быть расставлены в строгом порядке. После этого для того, чтобы вспомнить необходимую информацию достаточно вспомнить комнату. Именно так и делал Цицерон, когда готовился к выступлению

Он гулял по своему дому, мысленно расставляя акценты, чтобы суметь вернуться к важному моменту по ходу своего выступления. Не стоит ограничиваться комнатой, можно попробовать размещать желаемую информацию на знакомой улице, рабочем столе или другом объекте, который вам хорошо известен. Метод ментальных карт, или метод Бьюзена, — это простой способ графического изображения информации при помощи схем

Часто этот метод называют майндмэппинг, из-за того что необходимо строить ассоциативные карты. Такой способ запоминания стал довольно популярным в последнее время. Подобные карты рекомендуют составлять психологи и различные тренеры для того, чтобы правильно ставить цели и понимать свои настоящие желания. Но первоначальная цель ментальных карт заключалась именно в том, чтобы быстрее запоминать и структурировать информацию. Для того чтобы составить натальную карту, вам понадобится:

Метод ментальных карт, или метод Бьюзена, — это простой способ графического изображения информации при помощи схем. Часто этот метод называют майндмэппинг, из-за того что необходимо строить ассоциативные карты. Такой способ запоминания стал довольно популярным в последнее время. Подобные карты рекомендуют составлять психологи и различные тренеры для того, чтобы правильно ставить цели и понимать свои настоящие желания. Но первоначальная цель ментальных карт заключалась именно в том, чтобы быстрее запоминать и структурировать информацию. Для того чтобы составить натальную карту, вам понадобится:

• Материал, который вы захотите изучить.
• Большой лист бумаги.
• Цветные ручки и карандаши.

После этого нарисуйте в центре листа символ или рисунок, который ассоциируется с темой, которую вы хотите запомнить, или отображает ее суть. После этого по направлению к центру рисуйте различные цепочки связей, которые отражают ту или иную сторону изучаемого объекта. В результате для того, чтобы вспомнить нужную информацию, вам не придется просматривать списки или читать пол-учебника. Вы сможете сразу вспомнить главную идею, посмотрев на нее в центре листа, а потом, двигаясь по отходящим ветвям, вспомнить конкретно то, что вам нужно.

Задания для самостоятельного решения

Задание 1. Преобразуйте выражение (m + n)2 в многочлен.

Решение:
(m + n)2 = m2 + 2mn + n2

Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.

Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64

Задание 3. Преобразуйте выражение (2×2 + 3×3)2 в многочлен.

Решение:
(2×2 + 3×3)2 = (2×2)2 + 2 × 2×2 × 3×3 + (3×3)2 = 4×4 + 12×5 + 9×6

Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.

Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25

Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.

Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2

Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.

Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625

Задание 7. Преобразуйте выражение (3×2 − y3)2 в многочлен.

Решение:
(3×2 − y3)2 = (3×2)2 − 2 × 3×2 × y3 + ( y3)2 = 9×4 − 6x2y3 + y6

Задание 8. Выполните умножение (x − y)(x + y)

Решение:
(x − y)(x + y) = x2 − y2

Задание 9. Выполните умножение (2x − y)(2x + y)

Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4×2 − y2

Задание 10. Выполните умножение (7 + 3y)(3y − 7)

Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49

Задание 11. Выполните умножение (x2 − 5)(x2 + 5)

Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25

Задание 12. Выполните умножение (a3 − b2)(a3 + b2)

Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4

Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)

Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6

Задание 14. Выполните умножение (9x − y2)(y2 + 9x)

Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81×2 − y4

Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)

Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3

Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)

Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19

Задание 17. Выполните умножение (4x + 1)(16×2 − 4x + 1)

Решение:
(4x + 1)(16×2 − 4x + 1) = (4x)3 + 13 = 64×3 + 1

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Как читать формулы сокращенного умножения

article>УÑимÑÑ Ð¿ÑоговаÑиваÑÑ ÑоÑмÑÐ»Ñ ÑокÑаÑенного вÑÑажениÑ:

1. РазноÑÑÑ ÐºÐ²Ð°Ð´ÑаÑов двÑÑ Ð²ÑÑажений Ñавна пÑÐ¾Ð¸Ð·Ð²ÐµÐ´ÐµÐ½Ð¸Ñ Ð¸Ñ ÑазноÑÑи и Ð¸Ñ ÑÑммÑ.
2. ÐвадÑÐ°Ñ ÑÑÐ¼Ð¼Ñ Ð´Ð²ÑÑ Ð²ÑÑажений Ñавен квадÑаÑÑ Ð¿ÐµÑвого плÑÑ Ñдвоенное пÑоизведение пеÑвого на вÑоÑое плÑÑ ÐºÐ²Ð°Ð´ÑÐ°Ñ Ð²ÑоÑого.
3. ÐвадÑÐ°Ñ ÑазноÑÑи двÑÑ Ð²ÑÑажений Ñавен квадÑаÑÑ Ð¿ÐµÑвого минÑÑ Ñдвоенное пÑоизведение пеÑвого на вÑоÑое плÑÑ ÐºÐ²Ð°Ð´ÑÐ°Ñ Ð²ÑоÑого.
4. СÑмма кÑбов двÑÑ Ð²ÑÑажений Ñавна пÑÐ¾Ð¸Ð·Ð²ÐµÐ´ÐµÐ½Ð¸Ñ ÑÑÐ¼Ð¼Ñ Ð¿ÐµÑвого и вÑоÑого на неполнÑй квадÑÐ°Ñ Ð¸Ñ ÑазноÑÑи.
5. РазноÑÑÑ ÐºÑбов двÑÑ Ð²ÑÑажений Ñавна пÑÐ¾Ð¸Ð·Ð²ÐµÐ´ÐµÐ½Ð¸Ñ ÑазноÑÑи пеÑвого и вÑоÑого на неполнÑй квадÑÐ°Ñ Ð¸Ñ ÑÑммÑ.
6. ÐÑб ÑÑÐ¼Ð¼Ñ Ð´Ð²ÑÑ Ð²ÑÑажений Ñавен кÑÐ±Ñ Ð¿ÐµÑвого плÑÑ ÑÑÑоенное пÑоизведение квадÑаÑа пеÑвого на вÑоÑое плÑÑ ÑÑÑоенное пÑоизведение пеÑвого на квадÑÐ°Ñ Ð²ÑоÑого плÑÑ ÐºÑб вÑоÑого.
7. ÐÑб ÑазноÑÑи двÑÑ Ð²ÑÑажений Ñавен кÑÐ±Ñ Ð¿ÐµÑвого минÑÑ ÑÑÑоенное пÑоизведение квадÑаÑа пеÑвого на вÑоÑое плÑÑ ÑÑÑоенное пÑоизведение пеÑвого на квадÑÐ°Ñ Ð²ÑоÑого минÑÑ ÐºÑб вÑоÑого.

ÐбÑÑение на кÑÑÑÐ°Ñ Ð¿Ð¾ маÑемаÑике â доÑога к ÑоÑоÑим оÑенкам в Ñколе и вÑÑÐ¾ÐºÐ¾Ð¼Ñ Ð±Ð°Ð»Ð»Ñ Ð½Ð° Ñкзамене.

Упражнения

«Живописная» экспертиза (Из книги Сергея Быльцова «Логические головоломки и задачи»)

Одному коллекционеру принесли картину, якобы принадлежащую перу кисти Антонио Канале, прозванному Каналетто. Коллекционер не был большим знатоком живописи и потому пригласил на экспертизу трёх специалистов. Эксперты высказали о картине следующие суждения:

• Первый: Это не только не Каналетто, но даже и не Гварди.
• Второй: Это не Каналетто, но это настоящий Алессандро Маньяско.
• Третий: Конечно, это не Маньяско, это, несомненно, Антонио Канале.

Впоследствии объективными методами авторство картины было установлено, и оказалось, что один из экспертов сказал правду, другой ошибся, а третий был прав наполовину. Кто автор картины?

Принцесса и Иванушка

В этом упражнении вам необходимо найти принцессу, исходя из имеющихся данных на табличках. История такова: в поисках принцессы, похищенной Кощеем, Иванушка оказался в старинном замке. Преодолев массу препятствий, он очутился в помещении, из которого вели три двери. Иванушка знал, что за какой-то из них находится принцесса, за другой сидит тигр, а за оставшейся дверью никого нет.

Cтатистика На весь экран

Предлагаем вам также пройти упражнение, которое отлично показывает, что наш мозг может находить и понимать смысл слов, даже если его пытаются намеренно запутать. Это происходит потому, что мы читаем не по буквам и слогам, а слова целиком и кроме того, смысл слов мы понимаем благодаря соседним словам и словосочетаниям, с которыми наш мозг сталкивался раньше.

Cтатистика На весь экран

А теперь предлагаем закрепить материал урока с помощью теста.

Что такое структурирование?

Структурирование материала — это процесс организации информации для ее запоминания, в результате которого элементы изучаемого материала связываются по смыслу в целостную группу или несколько таких групп. Структурирование можно использовать для запоминания любой информации: больших или малых объемов, текста и цифр, учебного или развлекательного материала. Причем организация материала может происходить как до, так и после процесса получения (или накопления) знаний.

К примеру, возьмем номер телефона, написанный сплошным текстом 89115439080. Чтобы ее запомнить в таком виде нужно будет сильно постараться. Но если номер переписать в другом виде, например, в таком: 8 (911) 543-90-80, то запомнить его не составит большого труда. Поэтому, начиная от простого номера телефона и заканчивая большими учебниками, любая запоминаемая информация нуждается в структурировании.

What is a^2-b^2 Formula?

The a2 — b2 formula is given as: a2 — b2 = (a — b) (a + b).

If you would like to verify this, you can just multiply (a — b) and (a + b) and see whether you get a2 — b2.

Verification of a2 — b2 Formula

Let us see the proof of a square minus b square formula. To verify that a2 — b2 = (a — b) (a + b) we need to prove LHS = RHS. Let us try to solve the equation:

a2 — b2 = (a — b) (a + b)

Multiply the binomials (a — b) and (a + b) we get

(a — b) (a + b)

=a (a + b) — b (a + b)

=a2 + ab — ba — b2

=a2 + 0 + b2

=a2 — b2

Hence Verified

a2 — b2 = (a — b) (a + b)

You can understand the a2 — b2 formula geometrically using the following figure:

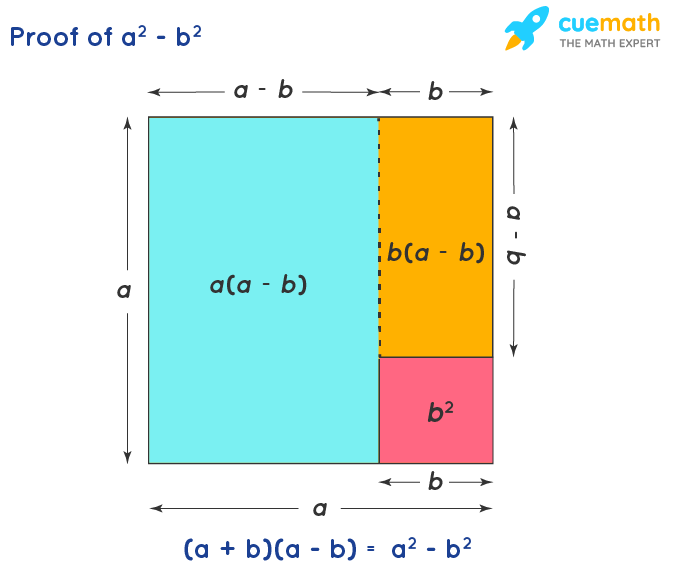
☛ Also Check:

• (a-b)^2 Formula
• (a+b)^2 Formula

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.

Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)2 = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4×2 + 6xy + 6xy + 9y2 = 4×2 + 12xy + 9y2

То есть выражение (2x + 3y)2 равно 4×2 + 12xy + 9y2

(2x + 3y)2 = 4×2 + 12xy + 9y2

Решим аналогичный пример, который попроще:

(a + b)2

Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)2 = (a + b)(a + b)

Выполним это умножение:

(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2

То есть выражение (a + b)2 равно a2 + 2ab + b2

(a + b)2 = a2 + 2ab + b2

Оказывается, что случай (a + b)2 можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4×2 + 12xy + 9y2

Как и в прошлый раз получили многочлен 4×2 + 12xy + 9y2. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)2 = 4×2 + 12xy + 9y2

Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)2 = 52 = 25

Второй способ:

(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9

Значит, (5a + 3)2 = 25a2 + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a2. Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

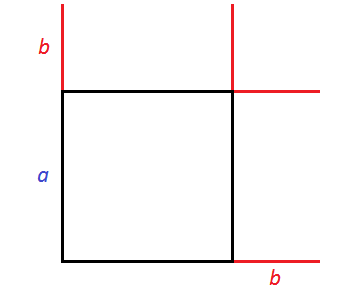
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

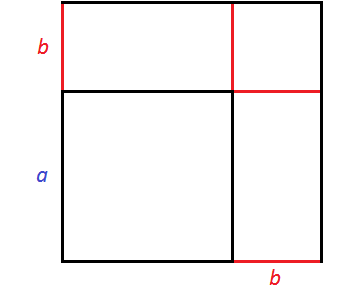
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

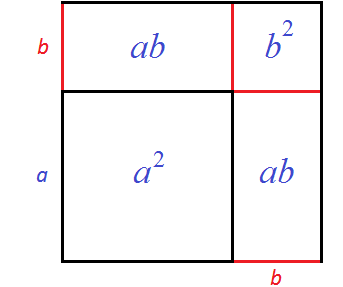
В результате получается следующая сумма площадей:

a2 + ab + ab + b2

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:

(a + b)2 = a2 + 2ab + b2

Шахматный подход[]

Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому неслучайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учётом цвета ячеек.

Файл:MKWik.jpg

Изображение схем построения магических квадратов.

Применение удвоенного квадрата в математике

Один из примеров применения удвоенного квадрата – в теории чисел. При решении некоторых задач, связанных с числами и простыми числами, удвоенные квадраты могут быть использованы для создания алгоритмов и методов решения.

В геометрии удвоенный квадрат может быть использован в качестве модели для изучения различных свойств квадратных фигур и их применения в практике. Благодаря особенностям своей структуры, удвоенный квадрат может быть использован для создания определенных форм и узоров, которые могут иметь практическое применение в архитектуре и дизайне.

Удвоенный квадрат также может быть использован в задачах, связанных с алгоритмами и программированием. Его особенности свойств могут быть использованы для разработки эффективных алгоритмов с минимальным количеством шагов и операций. Кроме того, удвоенные квадраты могут быть использованы в качестве надежной системы кодирования и шифрования информации.

• В теории игр удвоенный квадрат может быть использован в качестве игрового поля для различных стратегических игр и пазлов. Его особенности и свойства могут быть использованы в качестве базы для разработки специальных алгоритмов и методов игры.
• В статистике удвоенный квадрат может быть использован для анализа данных и моделирования различных статистических процессов. Его геометрические и числовые свойства могут быть использованы для разработки моделей и методов статистического анализа данных.
• В искусстве и дизайне удвоенный квадрат может быть использован в качестве основы для создания искусственных узоров и фигур. Благодаря своим геометрическим и числовым свойствам, удвоенные квадраты могут быть использованы для создание интересных и оригинальных дизайнов.

Методы структурирования

При существующем росте информации от человека требуют совершенствования умений работы с ней.

При работе с информацией важно:

1. Уметь осмысленно изучать доступный материал: выделять основную мысль и второстепенную.
2. Проводить анализ, сравнение, синтез полученной информации.
3. Выявлять причинно-следственные связи.
4. Проверять данные на истинность или верифицировать их.
5. Формулировать мысли, ответы на вопросы.
6. Приводить актуальные и выверенные доказательства утверждений.
7. Конструировать план, грамотно формулировать выводы.

Для этого используют технологии структурирования информации. Они представляют собой виды информационного моделирования. Можно изменить форму представления информации при неизменности ее содержания.

Исследователи изучали память человека и выделили несколько способов и методик по структурированию информации. Они помогают запоминать информацию быстрее и удобнее.

Римская комната или метод Цицерона

Метод римской комнаты или Цепочка Цицерона заключается в следующем: те объекты, которые надо запомнить, следует мысленно расставить в знакомой комнате в строго определенном порядке. Потом достаточно просто вспомнить эту комнату. И необходимая информация воспроизведется в памяти.

Считают, что так делал Цицерон, когда готовился к выступлениям. Он прогуливался по своему дому и мысленно размещал ключевые моменты своего выступления в нем.

Вместо комнаты можно использовать знакомую улицу, рабочий стол или любые другие объекты. Главное, чтобы их структура была хорошо известна человеку, которому нужно запомнить информацию.

Карты памяти или метод Тони Бьюзена

Карты памяти по-другому называют ментальными картами, диаграммами связей, интеллект-картами, ассоциативными картами или mind mapping.

Этот метод был предложен в 1974 году, когда опубликовали книгу «Работай головой».

Выделяют области применения карт памяти:

• планирование;
• обучение;
• мозговой штурм;
• запоминание;
• принятие решений и так далее.

Интеллект-карты решают различные задачи: систематизация учебных и рабочих процессов, управление деятельностью человека, распределение материала.

Такой метод структурирования информации предполагает изображение структуры информации с помощью блок-схемы.

Блок-схемой называют такой тип схем, который описывает алгоритмы или процессы, где отдельные шаги изображают в виде блоков различной формы. Они соединяются линиями, которые указывают на наличие связи между понятиями, действиями и знаменуют направление дальнейшего продвижения по информационному полю.

Информация разбивается на блоки и модули по выделенным основаниям и критериям.

Метод позволяет направлять человека к различной информации внутри блоков и модулей и между ними. В процессе используют разные источники и гиперссылки.

Чтобы построить карту памяти вручную, нужно выполнить определенные действия:

1. Взять материал, который нужно запомнить, и белый лист бумаги, ручку, цветные карандаши.
2. В центре листа изобразить любой символ или картинку. На ней наглядно представить название или содержание материала.
3. От центра листа к краям нарисовать цепочку связей, которая будет отражать структуру информации.

Существуют специальные программы, которые позволяют организовывать интеллект-карты по разработанным шаблонам.

Метод классификации

Под классификацией информации понимают создание иерархически организованной системы элементов, которые обозначают объекты или процессы реального мира. Их упорядочивают по признаку сходства или различия признаков, которые отражают выбранные свойства объектов.

Виды классификации:

• естественная или натуральная — выполняется по существенным признакам, которые характеризуют внутреннюю общность объектов или процессов;
• искусственная — по внешним признакам для упорядочивания некоторого множества объектов или процессов.

Принципы классификации:

1. Для каждой операции деления на классы допускают применение одного основания классификации.
2. Объем делимого понятия должен соответствовать полученным в результате деления классам.
3. Результаты деления понятий должны взаимно исключать друг друга.
4. Понятия делят последовательно.

Классификации бывают:

• простыми или одноуровневыми;
• сложными, которые представляют таблицами;
• иерархическими.

Помимо табличного варианта представления информации, для наглядного отображения состава и структуры данных используют графы.

В этом случае вершины или узлы графа обозначают моделируемые объекты, а связи между ними — дугами или ребрами графа.

Связи между объектами называют отношениями.

Симметричную связь обозначают отрезком, а несимметричную — стрелкой.

Дополнительные формулы сокращенного умножения

Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.

Бином Ньютона

Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:

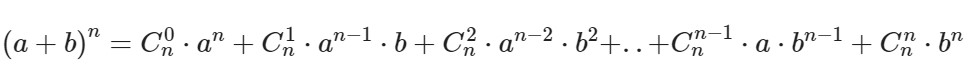
Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:

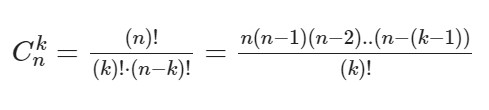
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.

Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Выглядит она так:

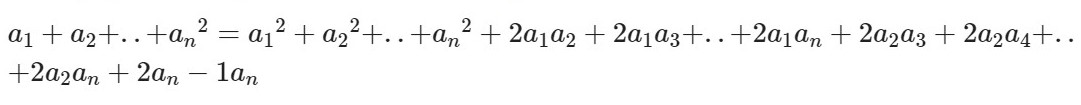
Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:

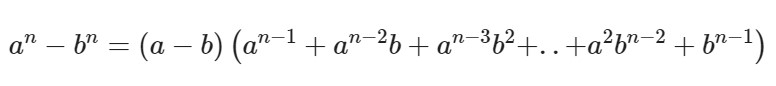
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.

Формула для четных показателей 2m:

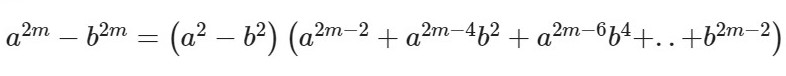
Формула для нечетных показателей 2m + 1:

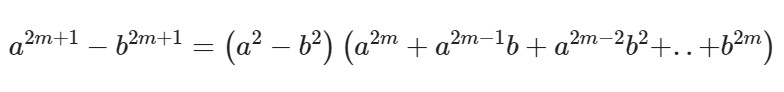
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.

Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.

Вопросы и ответы

И напоследок несколько ответов на часто задаваемые вопросы.

Для чего нужны формулы сокращенного умножения?

Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.

В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.

Как появились формулы сокращенного умножения?

Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.

Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.

Сколько всего формул сокращенного умножения?

Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.

Почему формулы сокращенного умножения изучают на алгебре в 7 классе?

Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.

Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.

Можно ли не использовать формулы сокращенного умножения?

Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.

Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.

Применение[править | править код]

В математике

Единичный квадрат используется как эталон единицы измерения площади, а также в определении площади произвольных плоских фигур. Фигуры, у которых можно определить площадь, называются квадрируемыми.

Теорема Пифагора первоначально формулировалась геометрически: площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Квадратами являются грани куба — одного из пяти правильных многогранников.

В математической физике символ квадрата может означать «оператор Д’Аламбера» (даламбериан) — дифференциальный оператор второго порядка:

u:=∂2u∂x2+∂2u∂y2+∂2u∂z2−1c2∂2u∂t2{\displaystyle \square u:={\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}}

Из теоремы Бойяи — Гервина следует, что любой многоугольник равносоставлен квадрату, то есть его можно разрезать на конечное число частей, из которых составляется квадрат (и обратно).

Графы:
K₄полный граф часто изображается как квадрат с шестью рёбрами.

Другие применения

Шахматная доска имеет форму квадрата и поделена на 64 квадрата двух цветов. Квадратная доска для международных шашек поделена на 100 квадратов двух цветов. Квадратную форму имеет боксёрский ринг, площадка для игры в квадрат.

Квадратный флаг Лима поделён на два чёрных и два жёлтых квадрата, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине.

Графика

Ряд символов имеют форму квадрата.

• Символы Юникода U+25A0 — U+25CF
• U+20DE ◌⃞ COMBINING ENCLOSING SQUARE
• ロ (Японский иероглиф «Ро» (катакана))
• 口 (Китайский иероглиф «рот»)
• 囗 (Китайский иероглиф «ограда»)

В Latex для вставки символа квадрата служат конструкции или .

В HTML, чтобы заключить произвольный текст в квадрат или прямоугольник, можно использовать конструкцию:

text; результат: text.

Что такое структурированные данные?

Когда дело доходит до информатики, структуры данных относятся к конкретным способам хранения и организации данных. Различные структуры данных имеют разные отношения между точками данных, но данные также могут быть неструктурированными. Что значит сказать, что данные структурированы? Чтобы сделать это определение более ясным, давайте рассмотрим некоторые из различных способов структурирования данных.

Структурированные данные часто хранятся в таблицах, таких как файлы Excel или Базы данных SQL. В этих случаях строки и столбцы данных содержат разные переменные или функции, и часто можно определить взаимосвязь между точками данных, проверив, где пересекаются строки данных и столбцы. Структурированные данные могут быть легко помещены в реляционную базу данных, а примеры различных функций в структурированном наборе данных могут включать такие элементы, как имена, адреса, даты, статистику погоды, номера кредитных карт и т. д. Хотя структурированные данные чаще всего представляют собой текстовые данные, они можно хранить такие вещи, как изображения и аудио, в виде структурированных данных.

Общие источники структурированных данных включают в себя такие вещи, как данные, собранные с датчиков, веб-журналы, сетевые данные, а также данные розничной торговли или электронной коммерции. Структурированные данные также могут создаваться людьми, заполняющими электронные таблицы или базы данных данными, собранными с компьютеров и других устройств. Например, данные, собранные с помощью онлайн-форм, часто сразу же вводятся в структуру данных.

Структурированные данные имеют долгую историю хранения в реляционные базы данных и SQL. Эти методы хранения популярны из-за простоты чтения и записи в этих форматах, поскольку большинство платформ и языков могут интерпретировать эти форматы данных.

В контексте машинного обучения структурированные данные легче обучать системе машинного обучения, поскольку закономерности в данных более явны. Определенные функции можно передать в классификатор машинного обучения и использовать для маркировки других экземпляров данных на основе этих выбранных функций. Напротив, обучение системы машинного обучения на неструктурированных данных, как правило, сложнее по причинам, которые станут ясны.

Структурирование информации в базах данных

База данных – это некая совокупность данных, которые совместно используются персоналом предприятия, региона, учащимися вуза и так далее. Задача баз данных состоит в том, чтобы можно было хранить большой объем информации и предоставлять их по первому запросу.

Правильно спроектированная база данных полностью исключает избыточность данных, благодаря чему риск хранения противоречивой информации сводится к минимуму. Исходя из этого, можно сказать, что создание баз данных в современном мире преследует две основные цели – это повышение надежности данных и понижении их избыточности.

Жизненный цикл программного продукта состоит из стадий проектирования, реализации и эксплуатации, но основной и ключевой является стадия проектирования. От того, насколько грамотно она продумана, насколько четко определены связи между всеми элементами, зависит информационная насыщенность и общая производительность.

Правильно спроектированная база данных должна:

• Гарантировать целостность данных.
• Исследовать, находить и удалять противоречивости.
• Обеспечивать легкое восприятие.
• Позволять пользователю структурировать информацию и вносить новые данные.
• Удовлетворять требования производительности.

Перед проектированием базы данных проводят тщательный анализ требований пользователей к будущему программному продукту. При этом от программиста требуется знание основных правил и ограничивающих факторов для того, чтобы грамотно выстроить логические взаимосвязи между запросами

Очень важно правильно проработать поисковой атрибут для того, чтобы пользователи могли по несортированным ключевым словам находить желаемую информацию. Также надо помнить, что чем больший объем информации хранит в себе база данных, тем важнее для нее вопрос производительности, ведь именно при максимальных нагрузках становятся видны все недочеты

Примеры задач с решением

Задача №3

Преобразовать трёхчлен в квадрат двучлена:

28xy + 49×2 + 4y2

Решение.

Поскольку квадраты находятся на втором и третьем местах, поменяем слагаемые между собой и подготовим выражение для применения формулы:

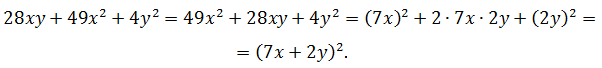
Ответ: (7x + 2y)2. 

Возведение во вторую степень суммы трёх и более слагаемых выполняется аналогично: необходимо возвести в квадрат каждый элемент, записать все возможные удвоенные произведения и сложить полученные результаты.

Правила возведения в степени более высоких порядков возникают, когда выполняется умножение одинаковых многочленов несколько раз.

Возможность выполнять возведение в квадрат больших чисел, не используя калькулятор, является одним из преимуществ сокращённого умножения.

Выполнить раскрытие скобок и упростить:

(x2 + 3x — 4y)2 — x4 — 9×2 — 16y2

Решение.

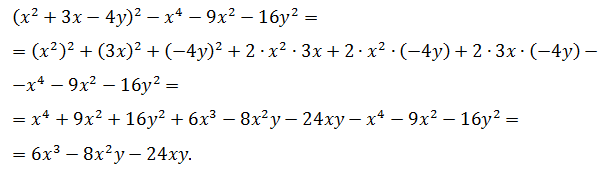
Ответ: 6×3 — 8×2 — 24xy.

Задача №5

Вычислить:

1032 + 1972

Решение.

Для каждого слагаемого применяется одно из правил возведения в квадрат, затем производится суммирование результатов:

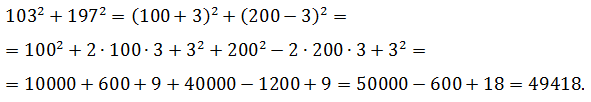
Решая квадратные уравнения, вместо поиска дискриминанта выделяют полный (точный) квадрат среди слагаемых, расположенных в левой части. В правую сторону собираются оставшиеся элементы.

Задача №6

Решить уравнение:

x2 — 4x — 5 = 0

Решение.

Первые два слагаемых левой части полностью удовлетворяют формуле квадрата суммы. Соотнеся их с соответствующими элементами правила, определяют, прибавляют и вычитают третье, затем сворачивают в точный квадрат, остальные члены алгебраической суммы переносят в правую сторону:

Решениями исходного уравнения являются корни уравнений

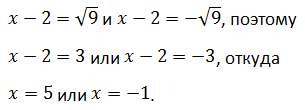
Ответ: x = 5 или x = -1.