Введение в пропорции в прямоугольниках
Когда дело доходит до понимания пропорциональных отношений в прямоугольниках, пропорции необходимы.Пропорции являются основой математики и используются в различных областях, таких как архитектура, инженерия и наука.Они полезны для решения реальных проблем и являются основой многих математических концепций.В этом разделе мы погрузимся глубже в мир пропорций в прямоугольниках, исследуя основы и расширяя наши знания по этой теме.
1. Понимание оснований: пропорции в прямоугольниках
В прямоугольнике соотношение длины к ширине постоянно.Это соотношение известно как соотношение сторон.Соотношение сторон прямоугольника можно рассчитать путем деления длины на ширину.Например, если прямоугольник имеет длину 10 единиц и ширину 5 единиц, соотношение сторон составляет 2: 1.Это означает, что на каждые 2 единицы длины существует 1 единица ширины.
2. Применение пропорций в прямоугольниках
Пропорции в прямоугольниках имеют много реальных приложений.В графическом дизайне соотношение сторон используется для определения размера и формы изображений.В архитектуре соотношение сторон используется для создания чертежи и планов этажей.В инженерии соотношение сторон используется для проектирования структур, которые могут противостоять напряжению и напряжения.В науке соотношение сторон используется для изучения поведения жидкостей и газов.
3. Пропорции в прямоугольниках и сходстве
Пропорции в прямоугольниках тесно связаны с концепцией сходства.Сходство относится к свойству двух фигур, которые имеют одинаковую форму, но не обязательно одинаковый размер.Говорят, что два прямоугольника похожи, если их соответствующие углы совпадают, а соответствующие их стороны пропорциональны.
4. Золотое соотношение и пропорции в прямоугольниках
Золотое соотношение — это математическая концепция, которая использовалась в искусстве, архитектуре и дизайне на протяжении веков.Это пропорция, которая встречается в природе, музыке и даже в человеческом теле.Золотое соотношение составляет приблизительно 1,618 и часто представлено греческой буквой phi ().В прямоугольниках золотое соотношение можно найти путем разделения длины прямоугольника на ширину.Говорят, что прямоугольники с золотым соотношением эстетически приятны и используются в искусстве и дизайне на протяжении веков.
Понимание пропорций в прямоугольниках имеет важное значение для тех, кто интересуется математикой, наукой, техникой или дизайном.Применение пропорций в прямоугольниках огромно, и концепция сходства и золотого соотношения тесно связана с темой.Понимая основы, мы можем расширить наши знания и найти творческие способы использования пропорций в нашей повседневной жизни. Введение в пропорции в прямоугольниках — Пропорции: понимание пропорциональных отношений в прямоугольниках
Введение в пропорции в прямоугольниках — Пропорции: понимание пропорциональных отношений в прямоугольниках
Приложения и использование
Этот термин чаще всего используется в отношении:
- Графика / изображение
- Соотношение сторон изображения
- Соотношение сторон дисплея
- Размер бумаги
- Стандартные форматы фотопечати
- Форматы кинофильмов
- Стандартный размер объявления
- Соотношение сторон пикселя
- Фотолитография : соотношение сторон вытравленной или осажденной структуры — это отношение высоты ее вертикальной боковой стенки к ее ширине.
- HARMST High Aspect Ratios позволяет создавать высокие микроструктуры без уклона.
- Код шины
- Размер шин
- Размер крыльчатки турбокомпрессора
- Соотношение сторон крыла самолета или птицы
- Астигматизм из оптической линзы
- Размеры наностержня
- Фактор формы (анализ изображений и микроскопия)
Вопрос-ответ:
Что такое Пифагоровы треугольники?
Пифагоровы треугольники — это треугольники, у которых длины сторон образуют простые числа и удовлетворяют теореме Пифагора.
Какие условия должны выполняться у сторон Пифагорова треугольника?
У сторон Пифагорова треугольника должно быть выполнено условие, что квадрат самой длинной стороны равен сумме квадратов двух остальных сторон.
Как найти Пифагоров треугольник с заданными сторонами?
Для поиска Пифагорова треугольника с заданными сторонами нужно использовать формулу, которая предлагает различные комбинации чисел, удовлетворяющие условию теоремы Пифагора.
Имеется ли у Пифагорова треугольника единственное решение?
Нет, у Пифагорова треугольника может быть несколько различных решений, так как условия теоремы Пифагора могут быть удовлетворены разными комбинациями чисел.
Какие треугольники называются Пифагоровыми примеры?
Треугольники, у которых длины сторон образуют пифагорову тройку, называются Пифагоровыми примерами. В таких треугольниках выполнено теоремы Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов.
Фильмы, записанные в формате 4:3 (или 1.33:1)
Как мы уже упоминали несколько строк назад, новая версия «Лиги справедливости» по версии Зака Снайдера — не первая и не последняя часть, в которой выбран формат 4:3.
Например, за последние 10 лет мы нашли несколько интересных игр, в которых использовалось это соотношение сторон, чтобы позже выйти на большой экран.
История брака
https://youtube.com/watch?v=pFg0Rk3L9SY
Не заходя слишком далеко сначала, в год 2019 Фильм попал в кинотеатры История одного брака. В нем театральному режиссеру и его жене-актрисе предстоит пережить сложный развод, затрагивающий все стороны их жизни. В дополнение к тому, чтобы бороться, чтобы дать стабильность своему маленькому сыну. Если вам интересно посмотреть этот фильм, вы можете сделать это через платформу Netflix.
Священник
https://youtube.com/watch?v=ZWI2cKrljfw
Годом ранее в г. 2018, нам удалось посмотреть фильм, носивший имя Священник. Эрнест Толлер — пастор-затворник крошечной церкви в Нью-Йорке. Он знакомится с Мэри, молодой девушкой, которая забеременела, и ее мужем, радикальным активистом-экологом. В отчаянии Мария попросит преподобного дать совет ее мужу. Фильм, который можно купить или взять напрокат на таких платформах, как Google Play или Apple TV.
Американский Мед
https://youtube.com/watch?v=y1SpWZm1PLc
Кроме того, в 2016, мы могли видеть драму под названием Американский Мед. Молодая женщина, постоянно скрывающаяся от правосудия, путешествует по стране, продавая подписки на журналы. Не слишком осознавая свою ситуацию, она оказывается вовлеченной в вихрь вечеринок до рассвета, который почти всегда выходит из-под контроля. Этот фильм можно купить или взять напрокат только через Google Play.
Сын Саула
https://youtube.com/watch?v=Kvux1G32C2g
На год раньше предыдущего, в г. 2015, попасть в кинотеатры Сын Саула, фильм, который вы можете посмотреть на платформе Amazon Prime Video. Этот фильм рассказывает об ужасах концлагеря Освенцим в 1944 году. Заключенный по имени Саул попытается спасти ребенка из крематория, к которому он будет относиться как к собственному сыну.
Отель Гранд Будапешт
https://youtube.com/watch?v=IImKsmIZ1VY
Еще одним довольно известным названием в 2014 году был Отель Гранд Будапешт. История, основанная на краже и возвращении картины эпохи Возрождения и решающей битве, которая возникает в семье, которая сталкивается друг с другом за огромное состояние. Фильм можно посмотреть на платформах HBO и Disney+.
Мамочка
https://youtube.com/watch?v=z0xSv2pq5yc
En 2014 фильм Мамочка, которым мы теперь можем наслаждаться на Amazon Prime Video. После смерти мужа молодая мать вынуждена одна воспитывать буйного сына. Все кажется потерянным, пока в доме не появляется новый сосед. Эта женщина интегрируется в жизнь этих матери и сына, чтобы оказывать им необходимую поддержку и помощь.
Идущий
https://youtube.com/watch?v=6C99zDU4Xp8
достигая 2013, мы могли видеть фильм под названием Идущий. Действие происходит в 60-х годах, когда молодая послушница собирается получить обеты и посвятить свою жизнь поискам веры, когда внезапно обнаруживает то, что мучило ее семью: ее предки были замешаны в ужасных действиях нацистов. Она решает отложить свои клятвы и отправиться в долгое путешествие в поисках истины. Этот фильм доступен для просмотра на платформе HBO.
Часть 3. Соотношения сторон видео на популярных платформах
Соотношение сторон является решающим фактором, который следует учитывать при создании контента для популярных платформ, таких как социальные сети, потоковые сервисы и сайты обмена видео. Каждая платформа имеет свои собственные спецификации и требования к соотношению сторон, и несоблюдение их может привести к плохому отображению или искажению контента.
Соотношение сторон Instagram
Предпочтительное соотношение сторон для Instagram — 1:1, также известное как квадратное соотношение сторон. Это означает, что размеры видео в Instagram должны быть равными, создавая квадратную форму. Однако Instagram также поддерживает другие соотношения сторон, например 4:5, 16:9 и 9:16 для вертикального видео. Тем не менее, лучшее соотношение сторон для Instagram — 1:1.
Соотношение сторон TikTok
TikTok — популярное приложение для обмена видео, которое имеет собственное предпочтительное соотношение сторон для видео. Рекомендуемое соотношение сторон для видео TikTok — 9:16, которое также известно как вертикальное или портретное соотношение сторон. Это означает, что размеры видео TikTok больше в высоту, чем в ширину, и предназначены для просмотра на мобильном устройстве без необходимости поворота. Вертикальный формат видео TikTok делает их идеальными для съемки крупным планом или демонстрации отдельных объектов, а также позволяет легко прокручивать ленту одной рукой.
Соотношение сторон Facebook
Facebook поддерживает различные соотношения сторон как для фотографий, так и для видео. Для фотографий рекомендуемое соотношение сторон 4:5, то есть в высоту больше, чем в ширину. Этот размер видео Facebook хорошо подходит для портретно-ориентированных изображений и обеспечивает хороший баланс между достаточно большим размером изображения и легкой видимостью в ленте новостей. Для фильмов с соотношением сторон Facebook поддерживает несколько соотношений сторон, включая 16:9, 9:16 и 1:1. Соотношение сторон 16:9 идеально подходит для широкоэкранных видео, а соотношение сторон 9:16 лучше всего подходит для вертикального или портретного видео. Соотношение сторон 1:1, создающее квадратное изображение, также часто используется для видео на Facebook.
Твиттер Соотношение сторон
Twitter также поддерживает различные соотношения сторон для фотографий и видео. Для фотографий рекомендуемое соотношение сторон 2:1 или 1200 × 600 пикселей. Это соотношение сторон обеспечивает широкий и панорамный вид, который хорошо подходит для изображений с альбомной ориентацией. Для видео Twitter поддерживает несколько соотношений сторон, включая 16:9, 1:1 и 9:16. Соотношение сторон 16:9 идеально подходит для широкоэкранного видео в Твиттере, тогда как соотношение сторон 1:1 обычно используется для квадратных видео. Соотношение сторон 9:16 лучше всего подходит для вертикального или портретного видео.
Сколько пикселей в формате 4 3?
Типичное соотношение сторон для изображений в формате 4:3 составляет 1024 x 768 пикселей или 8 x 6 дюймов.
Полезные дополнительные сведения: * Соотношение сторон определяет соотношение ширины к высоте изображения. * Формат 4:3 идеально подходит для стандартных мониторов и телевизоров, поскольку он соответствует их физическому соотношению сторон. * Другие распространенные соотношения сторон для изображений включают 16:9 (широкоэкранный) и 3:2 (с кадрированием)
* Знание соотношения сторон изображения важно для правильного отображения и гармоничной композиции. * Для достижения наилучших результатов изображения должны создаваться с правильным соотношением сторон или обрезаться до желаемого формата
Напоследок
В плане удобства для работы и видеоигр, нет совершенно никакой разницы, какое разрешение монитора вы будете использовать – это скорее дело привычки. Документы Word или таблицы Excel, равно как и современные игры, одинаково корректно отображаются на экране любого размера и с любым соотношением сторон.
Исключение здесь, пожалуй, только олдскульные «ламповые» игры (например, третьи «Герои меча и магии» в которые некоторые до сих пор играют), где современные разрешения мониторов, в списке поддерживаемых, отсутствуют в принципе – если это «родная» сборка, не мод, доработанный энтузиастами.
Вот, собственно, и все на сегодня.
Мерные стаканы
У опытных хозяек на кухне, как правило, есть специальные мерные стаканы, позволяющие не заниматься вычислениями, сколько это — 1/2 стакана на самом деле грамм. Сейчас мерные стаканы представлены в магазинах в широком ассортименте. Их делают из стекла или пластика, на внешней стороне нанесены шкалы. Причем шкал на одном стакане может быт несколько — отдельно для каждого типа продуктов. Более того, на одной и той же шкале иногда отмечают не только объем в миллилитрах, но и вес в граммах, а иногда и объем в стаканах. Такое приспособление существенно облегчает жизнь кулинару и снижает риск фатальных ошибок.
Применение конгруэнтности и Подобие треугольников
Соответствие и подобие треугольников имеют практическое применение в различных областях, таких как архитектура, инженерия и графический дизайн. Например, архитекторы используют конгруэнтность и сходство, чтобы убедиться, что разные части здания пропорциональны и идеально подходят друг к другу. Инженеры используют свойства треугольников для расчета устойчивости и прочности конструкций, таких как мосты и небоскребы. Графические дизайнеры используют принципы сходства и симметрии для создания гармоничных и визуально приятных макетов и композиций.
Понятия конгруэнтности и подобия треугольников также имеют образовательное значение, поскольку они развивают навыки критического мышления, решения проблем, и логические рассуждения. Они помогают учащимся развивать пространственное мышление, навыки визуализации и понимание красоты и симметрии геометрических фигур. Усвоив эти понятия, учащиеся смогут лучше разбираться в математике и применять свои знания к другим предметам и реальным ситуациям.
| Сходства треугольников | Конгруэнтность треугольников |
|---|---|
| Треугольники с одинаковыми углами | Треугольники одинаковой формы и размера |
| Постулаты подобия AA (угол-угол) или SSS (сторона-сторона-сторона) могут быть использованы для доказательства сходства | SSS (сторона-сторона-сторона), SAS (сторона-угол-сторона) , и постулаты конгруэнтности ASA (Angle-Side-Angle) можно использовать для доказательства конгруэнтности |
| Подобные треугольники имеют соответствующие стороны в одинаковом соотношении | Конгруэнтные треугольники имеют соответствующие стороны и углы, равные по размеру |
В целом, понятия конгруэнтности и подобия треугольников необходимы для изучения геометрии и имеют множество приложений и практических использует в различных областях. Понимая эти концепции и осваивая свойства треугольников, мы можем улучшить наше понимание мира природы и оценить красоту и симметрию математических фигур.
Как учить пропорциям?
Принципы обучения пропорциям
При преподавании пропорций необходимо стремиться к наглядному и практическому подходу. Представление реальных жизненных примеров облегчает понимание. Соотношения присутствуют везде, например:
- Кулинария: Рецепты часто используют соотношения для смешивания ингредиентов.
- Спорт: Команды используют соотношения для определения игровых стратегий.
- Искусство: Художники используют соотношения, чтобы создавать гармоничные композиции.
Интерактивные методы обучения
Практические задания и манипуляции с физическими объектами могут улучшить понимание пропорций. Например:
- Сравнение фигур: Пусть ученики сравнивают размеры и формы фигур и определяют их соотношения.
- Моделирование: Позвольте ученикам создавать модели, используя соотношения, например, используя кубики или блоки.
- Эксперименты по смешиванию: Пусть ученики проводят эксперименты со смешиванием жидкостей или сыпучих веществ, изучая соотношения ингредиентов.
Включив эти подходы в обучение, можно сделать концепцию пропорций более понятной и увлекательной.
Размеры фото на документы
- Для фото на паспорт РФ и другие документы установлены стандартные размеры. Также к ним предъявляется ряд других требований.
- На паспорт РФ: 3,5х4,5 см. Нередко люди сталкиваются с проблемой, когда их фото не принимают в паспортном столе. Зачастую это происходит потому, что многие приносят фото 3х4 см «по старой памяти». Сейчас это уже не является актуальным.
- На заграничный паспорт: 3,5х4,5 см
- На медицинскую книжку, студенческий билет, пенсионное удостоверение, временную регистрацию, зачетную книжку, пропуск, удостоверение, военный билет требуется фото 3х4 см
- На визу Шенген 3,5х4,5 мм
Также для фото на документы установлены цветность, величина головы, и поля над ней, наличие/отсутствие уголка, требования к фону и текстуре бумаги. Все эти аспекты уточняются в организациях, принимающих документы.
Что символизирует треугольник в математике — часто задаваемые вопросы
В: Что такое треугольник символ треугольника в математике?
A: Символ треугольника в математике — это геометрическая фигура, представляющая трехстороннюю фигуру, каждая сторона которой соединена вершиной.
Q: Что символизирует прямоугольный треугольник в математике?
A: Прямоугольный треугольник в математике символизирует треугольник с одним углом, равным 90 градусам, или прямым углом. У него есть два катета, которые перпендикулярны друг другу, и гипотенуза, которая является самой длинной стороной треугольника.
В: Что символизирует равносторонний треугольник в математике?
A: Равносторонний треугольник в математике символизирует тип треугольника, в котором все три стороны равны по длине, а все углы равны 60 градусам.
Q: Что символизирует равнобедренный треугольник по математике?
A: Равнобедренный треугольник в математике символизирует треугольник, две стороны которого имеют одинаковую длину, а два угла, противоположные этим сторонам, равны.
Q: Что означает разносторонний треугольник символизировать в математике?
A: Разносторонний треугольник в математике символизирует тип треугольника, в котором ни одна из сторон не равна по длине, а все три угла различны.
Q: Почему треугольник важен по математике?
A: Треугольник имеет важное значение в математике, поскольку он составляет основу различных геометрических фигур. Он также помогает вычислять площади многоугольников, измерять расстояния и углы и решать математические задачи
Пифагоровы треугольники: примеры и объяснение
Пифагоровы треугольники обладают одним из самых известных математических соотношений, известным как теорема Пифагора:
Для любого прямоугольного треугольника с гипотенузой c и катетами a и b выполняется следующее уравнение:
a2 + b2 = c2
Таким образом, длина гипотенузы (самой длинной стороны) всегда является квадратом целочисленной длины одного катета плюс квадратом целочисленной длины другого катета.
Примеры Пифагоровых треугольников:
- 3, 4, 5 – самый простой и известный пример Пифагорова треугольника, где a = 3, b = 4 и c = 5.
- 5, 12, 13 – еще один пример Пифагорова треугольника с целыми сторонами.
- 8, 15, 17 – третий пример Пифагорова треугольника, где a = 8, b = 15 и c = 17.
- 7, 24, 25 – еще один пример Пифагорова треугольника, где a = 7, b = 24 и c = 25.
Существует бесконечное количество Пифагоровых треугольников, и они могут быть увеличены в размерах и пропорциях. Они имеют широкие применения в различных областях, включая геометрию, физику, архитектуру и дизайн.
Требования к фото на документы для паспорта РФ
 В соответствии с приказом ФМС России от 2 сентября 2011 г внесены изменения в требования к формату фотографии для паспорта гражданина Российской Федерации. Старые форматы могут считаться недействительными с момента вступления приказа в силу.
В соответствии с приказом ФМС России от 2 сентября 2011 г внесены изменения в требования к формату фотографии для паспорта гражданина Российской Федерации. Старые форматы могут считаться недействительными с момента вступления приказа в силу.
Новые требования к фотографии в паспорте РФ в большей степени коснулись цвета фотографии. Если в старых паспортных правилах СССР, а затем и Российской Федерации строго установлен формат черно-белой фотографии, то в новых правилах это ограничение снимается и приоритет отдается цветным фотографиям вместо черно-белых. Но вы по-прежнему можете печатать как в черно-белом, так и в цветном режиме.
Размер фотографии на документ Паспорт гражданина РФ определен — 3,7 на 4,7 см.
Изменения коснулись и пропорций лица по сравнению с общей площадью фото. Если раньше на фото в обязательном порядке должна была быть сфотографирована часть тела человека, а именно плечи и часть груди, то в новых правилах основной упор делается на лицо. Он должен занимать не менее трети свободного пространства фотографии.
Пропорции головы относительно фотографии не менее 80%. Точные размеры головы испытуемого составляют от 3,2 до 3,6 см в высоту и от 1,8 до 2,5 см в ширину. При этом размер свободного пространства над головой должен составлять 0,5 см (допускается погрешность до 1 мм.)
Таким образом, на фотографии нового образца мы увидим только голову и шею испытуемого. Плечи при таком варианте не вписываются в каркас.
Дополнительные требования включают сплошной белый фон и глянцевую бумагу плотностью не менее 170 для фотопечати. Этот пункт перенесен из старых правил без изменений. На иллюстрации вы можете увидеть образец, отвечающий всем требованиям к фото для документов — паспорт гражданина РФ.
Таблица мер и весов
Довольно часто в кулинарных рецептах указывается количество того или иного ингредиента не в граммах, а в стаканах. Но случается, что под рукой стакана нет, а любимое блюдо приготовить хочется. В этом случае можно использовать весы. Главное — разобраться, сколько грамм продукта содержится в одном стакане. Затем можно рассчитать необходимый объем продукта. Часто в стаканах измеряют сыпучие продукты — крупу, соль, сахарный песок. Используя самый простой стеклянный стакан, объем которого равняется мл, мы на самом деле можем отмерить необходимое количество грамм сахара
Однако следует обратить внимание на то, что в рецептах часто используется не стандартный стакан, объем которого равняется мл, а граненный, емкость которого составляет мл. Если у вас на кухне есть весы, вполне можно обойтись и без стаканов. Остановимся на одном примере
Остановимся на одном примере.
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: 1 СТАКАН воды 1/2 ч.л КУРКУМЫ каждое утро БОКА и ЖИВОТ уходят, Кожа как в Молодости.
Прямой угол при строительстве. Нужна лишь веревка и помощь египтян.
При любой стройке часто сталкиваешься с проблемой разметки прямого угла на местности. Несомненно, что существуют всевозможные лазерные приборы, которые эту проблему решают на раз два. Они удобны и практичны. Но имеют один существенный недостаток — цена. Если вы профессионал — тогда — да, этот прибор незаменим. Ну а если любитель, и нужно всего пару раз построить прямой угол, то лишние расходы не к чему. Всегда можно обойтись веревкой, как делали с незапамятных времен. Даже египетские пирамиды строили с помощью этого способа и это до сих пор не потеряло актуальности.
Есть метод, который вполне рабочий и основан он на школьной геометрии. Допустим вам нужно поставить, грубо говоря, столбы под прямым углом друг к другу(угол забора). Этот способ я применял, когда делал на своем участке стол и вбивал трубы в землю. Конечно можно было и на глаз, но так как с этим у меня всегда была беда, то воспользовался обычной веревкой. Главное в этом, чтоб она не растягивалась, вот и все. У меня под рукой оказался мягкий тонкий провод, что вполне подходило под эти задачи.
Суть основывается на, так называемых, египетских треугольниках. Их еще называют Героновыми, Евклидовыми, Пифагоровыми. Не будем вдаваться в подробности, отмечу лишь, что зачастую египетские — это частное от всех остальных. Лишь Пифагоровы тройки точно отвечают нашим требованиям.
Вот этот замечательный треугольник. Его стороны являются целым числом, что нам и нужно. Соответственно. Берем веревку и строим с помощью нее эту фигуру на земле. И не обязательно откладывать именно 3 метра, 4 и 5. Самое главное — соблюсти пропорции. За единицу измерения можно взять и полметра, а можно и любую другую удобную длину. Для примера — полуметровые соотношения — 1,5 м 2 м и 2,5 м. Просто, чем больше размеры — тем точнее наши построения.
Итак. Забиваем столб, от которого нам и надо построить прямой угол. От него отмечаем 3 метра и забиваем колышек на этом месте. К колышку привязываем веревку в пять метров а к столбу — четырехметровую. Связываем свободные концы друг с другом и натягиваем веревки, чтобы обе ни где не провисали. Когда найдем это место — туда колышек и все. Построения закончены — прямой угол у нас имеется. А дальше по линиям веревки забиваем столбы на нужном нам расстоянии.
Просто, дешево, быстро. Главное в этом деле — не спешить, и чем больше точность в отрезках веревки — тем ближе угол к 90 градусам.
Кстати, есть еще пару методов на основе треугольников и знаний геометрии, но об этом как нибудь в следующий раз. А на этом пока все.
Определение размера кадра записи
В англоязычной среде для описания отношения ширины кадра к высоте в большинстве случаев используется термин Display Aspect Ratio (или более кратко — DAR). DAR состоит из двух составляющих:
- Pixel — отношение пиксельных сторон. Учитывая, что в нынешних диджитал-форматах обычно применяются лишь пиксели квадратной формы, то по большей части для видеозаписей значение составит 1:1.
- Storage — отношение численности пикселей в горизонтальном направлении к численности пикселей в вертикальном (данные числа показываются в файловом видеоразрешении).

Измерить рулеткой не получится
Помножив Pixel на Storage, у нас получится DAR – настоящее соотношение сторон записи.
Теперь перейдём к конкретике. Допустим, необходимо выполнить рассчет для файла в AVI-расширении с разрешением видео в 640х480. Для определения SAR, нам придётся поделить ширину видеозаписи в 640 пикселей на высоту 480 для получения простой дроби. В итоге будет 4/3. Ввиду того, что Pixel Aspect Ratio равняется 1, то 4:3 — это и есть размер кадра нашей записи.
Неправильные пропорции изображения в компьютерной игре
Кстати, величины Display Aspect Ratio и Storage Aspect Ratio оказываются идентичными не во всех случаях. Предположим, в форматах DVD и VCD видеофайлы оцифровывается с применением нестандартных точек (значение не равняется 1:1). Для более отчётливого понимания разберем Display Aspect Ratio для DVD-формата с довольно популярным разрешением 720х576. В данной ситуации Storage Aspect Ratio равен 5:4, а Pixel Aspect Ratio, исходя из видеостандарта, будет 16:15. Если умножить данные величины друг на друга, то Display Aspect Ratio выйдет 4:3. Однако это скорее исключение из правила.
Как масштабировать прямоугольники пропорционально
Когда дело доходит до работы с прямоугольниками, масштабирование их пропорционально является важным навыком.Независимо от того, разработаете ли вы веб -сайт, создаете графику или работаете над физическим проектом, понимание пропорциональных отношений в прямоугольниках имеет решающее значение.
Масштабирование прямоугольника пропорционально означает, что вы меняете его размер, сохраняя при этом его первоначальное соотношение сторон.Это важно, потому что это гарантирует, что прямоугольник не искажается или растягивается из формы.Вместо этого он изменяется таким образом, что поддерживает свои первоначальные пропорции. Есть несколько способов масштабировать прямоугольники пропорционально, и вот некоторые углубленные объяснения того, как это сделать:
Есть несколько способов масштабировать прямоугольники пропорционально, и вот некоторые углубленные объяснения того, как это сделать:
1. Используйте инструмент масштабирования: многие программные приложения проектирования, такие как Adobe Illustrator или Sketch, имеют встроенные инструменты масштабирования.Эти инструменты позволяют вам выбрать объект, такой как прямоугольник, и масштабировать его пропорционально путем перетаскивания одного из его углов при удержании клавиши Shift.Это гарантирует, что соотношение сторон остается прежним, пока вы корректируете размер.
2. Рассчитайте соотношение сторон. Если вы работаете с физическим прямоугольником, таким как лист бумаги, вы можете рассчитать его соотношение сторон, чтобы убедиться, что вы масштабируете его пропорционально.Для этого разделите более длинную сторону прямоугольника на более короткую сторону.Например, если у вас есть лист бумаги, который составляет 8 дюймов на 11 дюймов, соотношение сторон составляет 11/8 или 1,375.Используйте это число, чтобы масштабировать прямоугольник вверх или вниз при сохранении его пропорций.
3. Используйте математику: если вы знаете размеры исходного прямоугольника и желаемые размеры нового прямоугольника, вы можете использовать математику для масштабирования ее пропорционально.Для этого разделите ширину и высоту нового прямоугольника по ширине и высоте исходного прямоугольника.Меньшее из двух полученных чисел является масштабным коэффициентом.Например, если оригинальный прямоугольник составляет 4 дюйма на 6 дюймов, и вы хотите масштабировать его до 8 дюймов на 12 дюймов, масштабный коэффициент составляет 2. Чтобы пропорционально масштабировать прямоугольник, умножьте оба размера исходного прямоугольника по шкалефактор
Понимание того, как пропорционально масштабировать прямоугольники, является важным навыком, независимо от того, работаете ли вы над физическими или цифровыми проектами.Поддерживая соотношение сторон, вы можете гарантировать, что ваши дизайны выглядят отполированными и профессиональными.
Как масштабировать прямоугольники пропорционально — Пропорции: понимание пропорциональных отношений в прямоугольниках
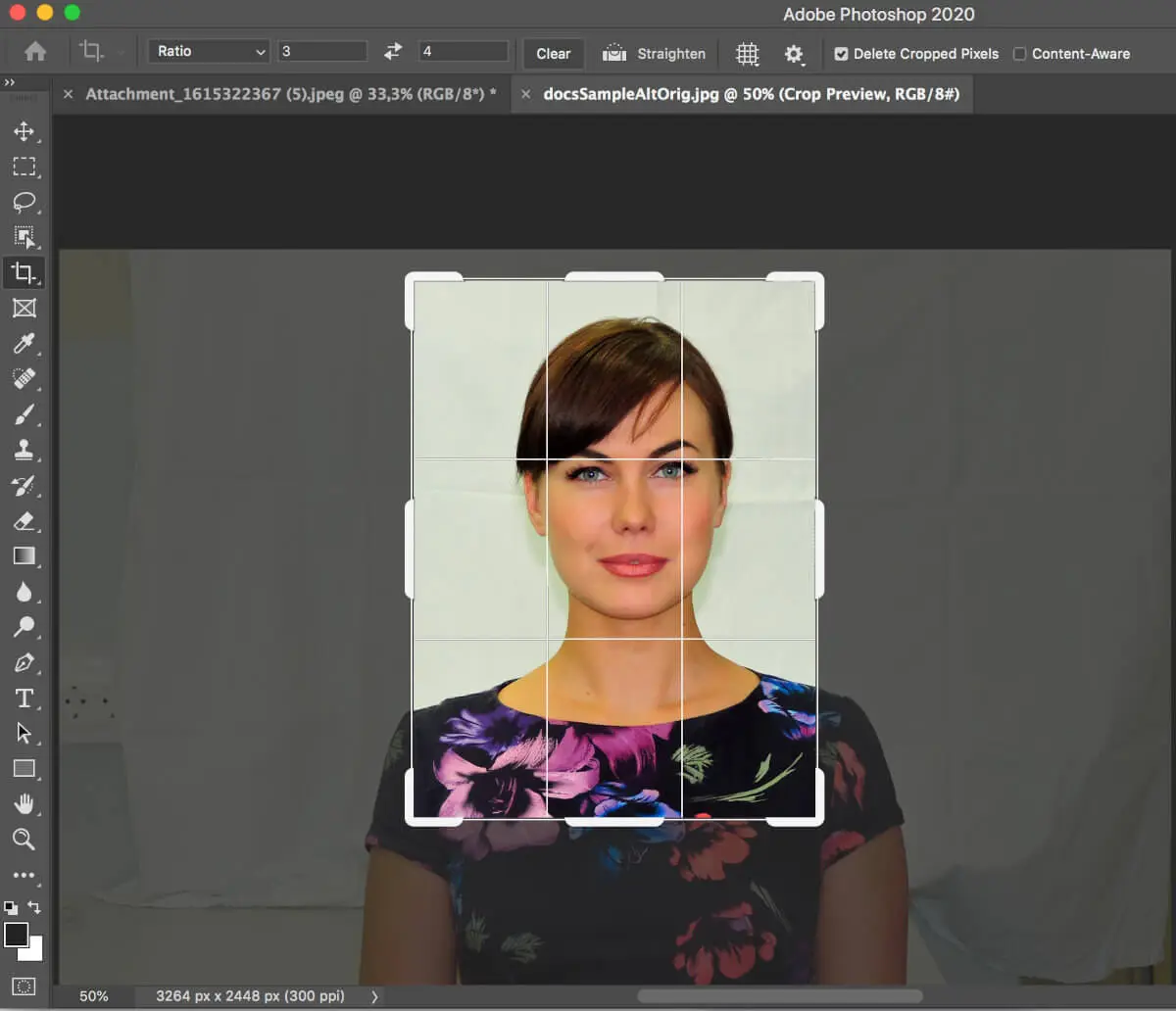
Как изменить размер фотографии до 3х4 см в фотошопе?
Если у вас есть фотошоп или аналогичный фоторедактор, вы можете самостоятельно обрезать фото 3х4 онлайн.
- Запустите фотошоп и выберите фотографию, которую нужно отредактировать, с помощью опции “Обзор”.
- Выберите инструмент “Кадрирование” на левой панели инструментов.
- Перетащите селектор кадрирования, удерживая лицо в центре. Изображение должно включать верхнюю часть туловища.
- Найдите поле «Соотношение» на верхней панели. Введите необходимое соотношение сторон: 3 по ширине и 4 по высоте.
- Нажмите Ввод. Ваше фото 3х4 на компьютере успешно обрезано!
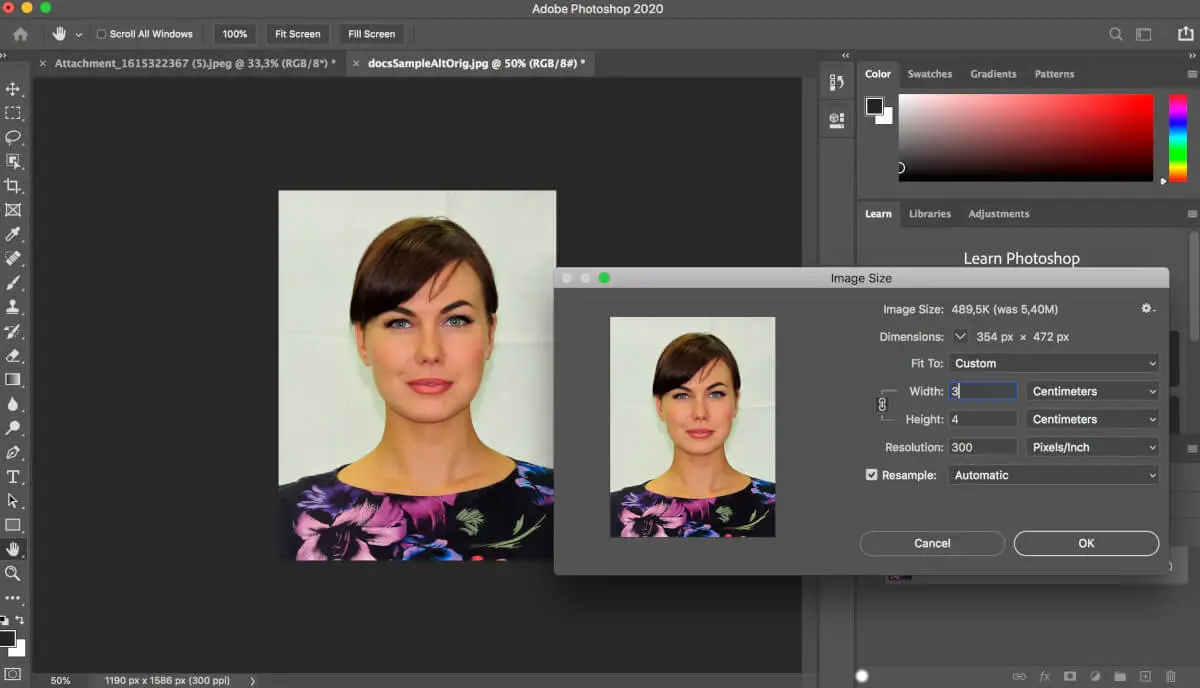
Чтобы установить правильный размер для печати, перейдите в раздел “Изображение”. Выберите размер снимка и установите ширину и высоту: 3×4 см.
Задайте разрешение минимум 300 точек на дюйм (оптимальным выбором является 600 точек на дюйм).
Ваше фото готово.
Прямоугольник: определение, свойства, основные формулы
Прямоугольник — параллелограмм, у которого все углы равны.
Отличие от параллелограмма есть в названиях сторон фигуры: в прямоугольнике длинную сторону принято называть длиной, а короткую — шириной, для сторон параллелограмма особенные наименования не используются.
Помимо всех свойств, присущих параллелограмму, у прямоугольника есть уникальные черты:
-
Диагонали прямоугольника равны.
-
Диагональ делит прямоугольник на два равных прямоугольных треугольника.
-
Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
-
Диагональ прямоугольника является диаметром описанной окружности.
-
Стороны прямоугольника одновременно являются и его высотами.
-
Вокруг любого прямоугольника можно описать окружность, т. к. сумма противоположных углов равна 180°.
Формулы для нахождения площади прямоугольника можно вывести из аналогичных для параллелограмма:
-
(т. к. высота, проведённая из вершины угла к противоположной стороне, совпадает с другой стороной прямоугольника).
-
(т. к. угол между сторонами — прямой, а ).
-
.
Это интересно
Золотой прямоугольник — это геометрическая форма, в которой отношение более длинной стороны к более короткой стороне равно соотношению всего прямоугольника к более длинной стороне. Такое соотношение примерно равно 1,618 и считается наиболее эстетичным и приятным для человеческого глаза.
Глупая ошибка строителей
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.
ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет
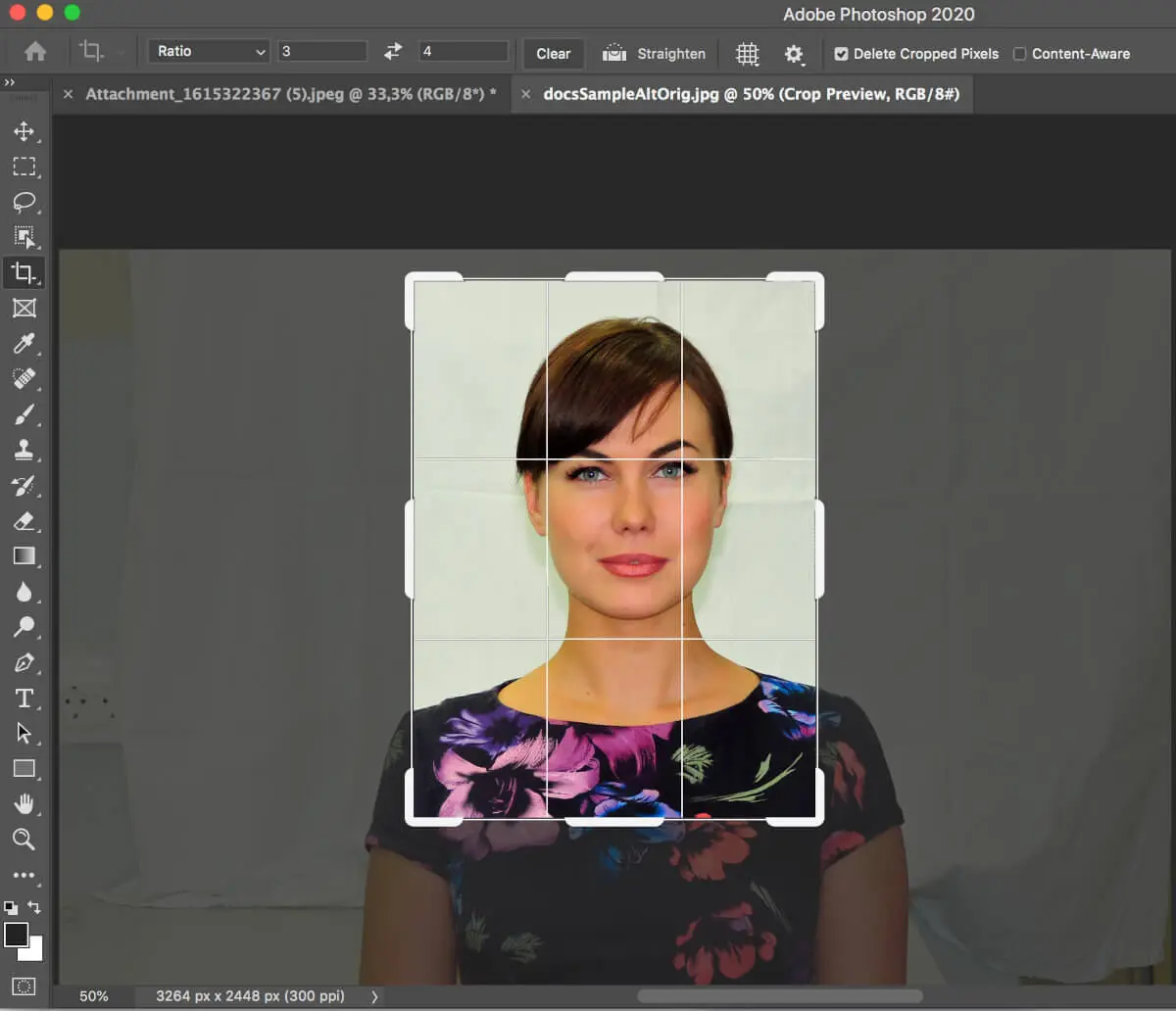
Как изменить размер фотографии до 3х4 см в фотошопе?
Если у вас есть фотошоп или аналогичный фоторедактор, вы можете самостоятельно обрезать фото 3х4 онлайн.
- Запустите фотошоп и выберите фотографию, которую нужно отредактировать, с помощью опции “Обзор”.
- Выберите инструмент “Кадрирование” на левой панели инструментов.
- Перетащите селектор кадрирования, удерживая лицо в центре. Изображение должно включать верхнюю часть туловища.
- Найдите поле «Соотношение» на верхней панели. Введите необходимое соотношение сторон: 3 по ширине и 4 по высоте.
- Нажмите Ввод. Ваше фото 3х4 на компьютере успешно обрезано!
Чтобы установить правильный размер для печати, перейдите в раздел “Изображение”. Выберите размер снимка и установите ширину и высоту: 3×4 см.
Задайте разрешение минимум 300 точек на дюйм (оптимальным выбором является 600 точек на дюйм).
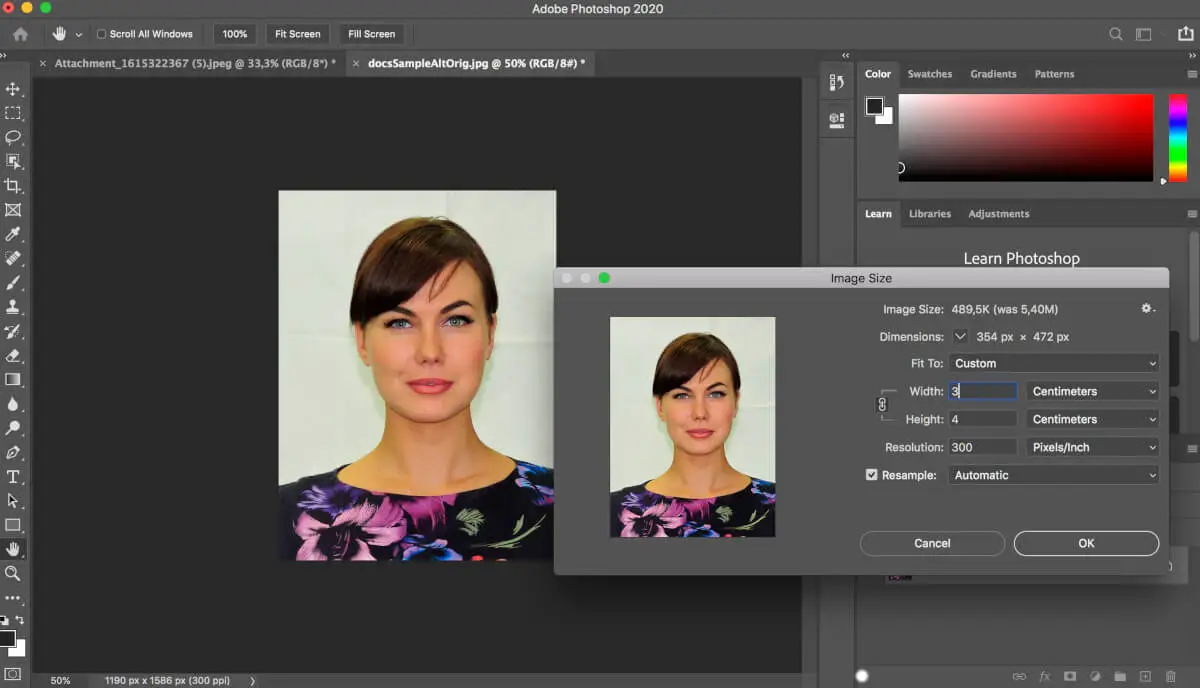
Ваше фото готово.
Такие разные стаканы
Следует начать с того, что ведь и стаканы бывают разные, и зачастую автор не указывает в своем рецепте, какой именно стакан он использует. Есть стаканы хайбол, средний объем которых в среднем 270 мл, но бывают экземпляры объемом и до 350 мл. А если автор использовал граненый стакан, то его объем ровно 200 мл. Часто именно их и используют в рецептах русскоговорящий контингент. Но что делать, если граненого стакана у вас нет, а приготовить блюдо очень хочется. Можно конвертировать стаканы в граммы, если у вас есть весы, а если весов нет, то конвертировать стаканы во что-то более общее, например в ложки. Тогда 1/4 стакана это сколько столовых ложек для этого рецепта? Сейчас разберемся.
Заключение
Теперь вы многое знаете о форматах роликов. Осталось упомянуть, какие пропорции применимы для Ютуба. В этом случае всё довольно просто: на веб-сайте и в приложении данного ресурса значение равняется 16:9, и если запись не соответствует данному стандарту, то на изображение накладываются лишние полосы, а видео теряет эффектность.
Каким же образом распознать неверные размеры кадра у видеозаписи? Если вы запустили ролик, сохранённый с неправильным значением, то сразу же заметите на экране одну из нижеперечисленных неисправностей:
- Некорректное изменение пропорций. То есть картинка кажется чрезмерно вытянутой или, наоборот, — расплющенной.
- Заметные полосы черного цвета по бокам или по горизонтали, либо черная рамка.

Ещё один пример дефекта
Бывает, что подобные неисправности появляются из-за некорректных параметров экрана, на котором запущена видеозапись. Но если все параметры корректны, а картинка на дисплее остаётся неправильной, необходимо отрегулировать формат проигрываемого файла. С помощью видеоредактора ВидеоМОНТАЖ вы за минуту разберетесь, как изменить размер кадра (пропорции видео). Просто скачайте эту программу для обработки видео и исправьте ошибки в пару кликов мыши.
Cохраните себе статью, чтобы не потерять:


























