Параллелограмм — его основные свойства, признаки и формулы

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный шкафчик.

Конспект урока «Прямоугольник. Свойство его сторон. Квадрат»

-Здравствуйте, мои дорогие дети! Сегодня мои друзья и помощники плюс и минус заняты очень важным делом. Присоединяйтесь к нашему турниру по поиску неисправностей. И нам необходимо знакомиться с новыми темами. Поэтому я решил объяснить вам это сам. Но прежде чем мы начнем, я прошу вас отгадать загадку.

У двери, за столом, в книге.

О какой фигуре мы сегодня говорим? Вы уже поняли, что речь идет о прямоугольниках.

Теперь внимательно посмотрите на экран. Что вы видите на экране?

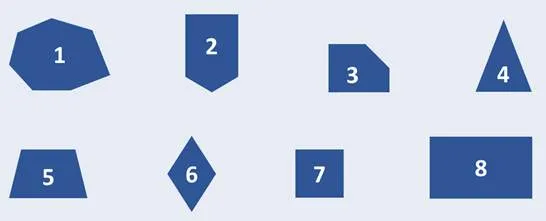
Конечно, эти фигуры можно назвать одним словом — многоугольники. Существуют фигуры с тремя углами, четырьмя углами, пятью углами и т.д.

Вы уже знакомы с темой углов. И помните, что углы бывают разные — прямые, тупые, острые.

А фигура, о которой мы сегодня поговорим, называется прямоугольником. Вы слышите это? Прямой угол. Если мы скажем, что это прямоугольник, то вы догадаетесь, что это означает, что у него прямой угол.

Посмотрите на наш план. Затем с помощью линейки посмотрите, какая фигура находится под прямым углом. Посмотрите на первую диаграмму.

Это шестиугольник. Давайте проверим его углы.

Как видите, эта фигура имеет прямой угол, а остальные фигуры — непрямые.

Посмотрите на вторую диаграмму: это пятиугольник.

У него два прямых угла, остальные три — непрямые.

Третий также является пятиугольником. У него три прямых угла. Четвертый — треугольник. Пятый — это стол.

Эти фигуры не имеют правильных углов.

Но седьмой и восьмой:.

Все эти фигуры имеют правильные углы.

Такие фигуры с прямыми углами называются прямоугольниками

Обратите внимание, что обе фигуры с правильными углами являются четырехугольниками, т.е. имеют четыре угла и четыре стороны. Конечно, существуют различные четырехугольники

Однако прямоугольник называется четырехугольником только в том случае, если все углы правильные

Конечно, существуют различные четырехугольники. Однако прямоугольник называется четырехугольником только в том случае, если все углы правильные.

А теперь я предлагаю вам познакомиться с интересными свойствами прямоугольника. Вам понадобятся линейка и компас.

Перед нами прямоугольник. Посчитайте верхнюю часть.

Она равна 6 см. Затем измеряется нижняя часть, т.е. сторона, противоположная верхней части. Поэтому она называется другой стороной и также равна 6 см.

Они составляют 2 см. Рассчитайте другую сторону. Они также составляют 2 см. Следовательно, равны ли противоположные стороны прямоугольника? Или это только прямоугольник. Проверьте другой прямоугольник.

Стороны равны и противоположные стороны равны.

Теперь мы можем с абсолютной уверенностью сказать, что у прямоугольника равные стороны. Поэтому, называя длины сторон прямоугольника, не обязательно называть каждую сторону. Одна длинная сторона и только одна сторона может быть подписана. Ведь вы знаете, что противоположные стороны прямоугольника равны. Поэтому, подписав одну из сторон, вы знаете, что другая сторона этого прямоугольника также будет такой же длины.

Признаки и свойства прямоугольника

Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:

• фигура является четырёхугольником, три угла которого равны 90°,
• представленный четырёхугольник — это параллелограмм с равными диагоналями,
• параллелограмм, который имеет по крайней мере один прямой угол.

Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.

Формулы для вычисления длины сторон

В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).

Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α угол между диагональю и длиной, β острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:

• С использованием диагонали и известной стороны: a = √(d ² b ²), b = √(d ² a ²).
• По площади фигуры и одной из её сторон: a = S / b, b = S / a.
• При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
• Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
• Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.

Периметр и площадь

Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:

• Через обе стороны: P = 2 (a + b).
• Через площадь и одну из сторон: P = (2S + 2a ²) / a, P = (2S + 2b ²) / b.

Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:

• Через длины обеих сторон: S = a*b.
• При помощи периметра и какой-либо одной известной стороны: S = (Pa — 2 a ²) / 2, S = (Pb — 2 b ²) / 2.
• По диагонали и углу β: S = 0,5 d ² sinβ.

Диагонали прямоугольника

В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:

1. Диагонали равны друг другу и делятся на два равных отрезка в точке их пересечения.
2. Диагональ определяется как корень суммы обеих сторон, возведённых в квадрат (следует из теоремы Пифагора).
3. Диагональ разделяет прямоугольник на два треугольника с прямым углом.
4. Точка пересечения совпадает с центром описанной окружности, а сами диагонали — с её диаметром.

Применяются следующие формулы для расчёта длины диагонали:

• С использованием длины и ширины фигуры: d = √(a ² + b ²).
• С использованием радиуса окружности, описанной вокруг четырёхугольника: d = 2 R.

Диагонали делятся пополам

Так как параллелограмм — это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.

У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.

Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.

Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам.

Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых
(рис.1).

Теорема 1. О свойстве сторон и углов параллелограмма. В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).

Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.

Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.

Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.

Доказательство. В самом деле, пусть а || b (рис.3).

Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD — параллелограмм, и следовательно, АВ = CD.

Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.

По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.

Пример 1. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.

Решение. По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию
$$\left\{\begin{matrix}
2x + 2y = 122
\\x — y = 25
\end{matrix}\right.$$
Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.

Пример 2.

Решение. Пусть условию задачи отвечает рисунок 4.

Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5.
Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 — 5 = 3 .
Итак, BD = 3 см.

Пример 3. Найти углы параллелограмма, зная, что один из них больше другого на 50°.

Решение. Пусть условию задачи отвечает рисунок 5.

Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.

Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.

х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.

Пример 4. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?

Решение. Пусть условию задачи отвечает рисунок 6.

АЕ — биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.

В этом разделе мы рассматриваем геометрический объект параллелограмм. Все элементы параллелограмма наследуются от четырехугольника, поэтому рассматривать их мы не будем. А вот свойства и признаки заслуживают детального рассмотрения. Мы разберем:

• чем признак отличается от свойства;
• рассмотрим основные свойства и признаки, которые изучают в программе 8 класса;
• сформулируем еще два дополнительных свойства, которые получим при решении опорных задач.

Площадь параллелограмма

Площадь параллелограмма — это пространство между четырьмя сторонами параллелограмма. Его можно рассчитать, зная длину основания и высоту параллелограмма и измерив их в квадратных единицах, таких как см 2 , м 2 или дюйм 2

Обратите внимание на следующий параллелограмм, представляющий основание и высоту

Рассмотрим параллелограмм ABCD с основанием (b) и высотой (h). Площадь параллелограмма вычисляется по формуле:

Площадь параллелограмма без высоты

Когда высота параллелограмма не известна, но площадь параллелограмма все же можно найти, если нам известен угол. Формула площади параллелограмма без учета высоты выглядит так:

Где a и b — стороны параллелограмма, а θ — угол между ними.

Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике

Здесь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе.

Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие.

Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.

1) Площади четырехугольников

Площадь параллелограмма

произведение основания на высоту

пороизведение сторон на синус угла между ними

полупроизведение диагоналей на синус угла между ними

Площадь трапеции

произведение полусуммы оснований на высоту

произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними

Площадь произвольного четырехугольника

Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними

• 2) Свойства параллелограмма
• В параллелограмме:
  противолежащие стороны и углы равны
• диагонали пересекаются и в точке пересечения делятся пополам
• 3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть
• 3) Cредняя линия в трапеции

  Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
  То есть и

• 4) Средняя линия в равнобедренной трапеции
• Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.
• То есть
• 5) Теорема с сдвиге диагонали в трапеции
• Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:
• трапеция  — равнобедренная равнобедренный
• 6) Четыре замечательные точки в трапеции
• Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.
• То есть точки M, N, K и P лежат на одной прямой

Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан.

Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список.

Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией.

В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.

Колпаков Александр Николаевич. Репетитор по математике.

Теорема о параллелограмме

Теорема: параллелограммы на одном основании и между одинаковыми параллелями имеют одинаковую площадь.

Доказательство: Предположим, что есть два параллелограмма ABCD и ABEF с одним и тем же основанием DC и между одинаковыми параллельными прямыми AB и FC.

Доказать: площадь параллелограмма ABCD = площадь параллелограмма ABEF.

На приведенном ниже рисунке два параллелограмма ABCD и ABEF лежат между одними и теми же параллельными прямыми и имеют одно и то же основание. Площадь ABDE является общей для обоих параллелограммов. Если присмотреться к двум треугольникам, △BCD и △AEF могут оказаться конгруэнтными.

BC = AE (противоположные стороны параллелограмма),

∠BCD = ∠AEF (это соответствующие углы, потому что BC || AE и CE являются секущими).

∠BDC = ∠AFE (это соответствующие углы, поскольку BD || AF и FD являются секущими).

Таким образом, по критерию ASA конгруэнтных треугольников. Эти два треугольника конгруэнтны, и они должны иметь равные площади.

площадь (BCD) = площадь (AEF)

⇒ площадь(BCD) + площадь(ABDE) = площадь(AEF) + площадь(ABDE)

⇒ площадь(ABCD) = площадь(ABEF)

Следовательно, параллелограммы, лежащие между одними и теми же параллельными прямыми и имеющие общее основание, имеют одинаковую площадь.

ПРЯМОУГОЛЬНИК — ЧЕТЫРЕХУГОЛЬНИКИ

Цель деятельности учителя	Создать условия для введения определения прямоугольника, изучения свойств прямоугольника
Термины и понятия	Прямоугольник, диагонали прямоугольника
Планируемые результаты
Предметные умения	Универсальные учебные действия
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики	Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в решении учебных задач. Регулятивные: проявляют познавательный интерес к изучению предмета. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: умеют контролировать процесс и результат учебной математической деятельности
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Учебник. • Задания для индивидуальной работы
I этап. Проверка домашнего задания
Цель деятельности	Деятельность учителя	Деятельность учащихся
Выявить трудности, возникшие при выполнении домашнего задания	(И/Ф) 1. Сформулируйте теорему Фалеса. 2. Сформулируйте свойства равнобедренной трапеции. 3. Решите устно задачи по готовым чертежам.	1. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. 2. В равнобедренной трапеции углы при основаниях равны, диагонали равны. 3. ∆ABC — равнобедренный. ∠BAC = ∠BCA = х°, как внутренние накрест лежащие при ВС || AD и секущей АС,∠BAD = ∠CDA = 2х°. Из прямоугольного ∆ACD: ∠CAD + ∠CDA = 90° => х = 30°. В трапеции ABCD ∠BAC = ∠CAD = 60°, ∠BCD = 120°
II этап. Изучение нового материала
Цель деятельности	Совместная деятельность
Ввести понятие прямоугольника, доказать свойства и признаки прямоугольника	1. Ввести понятие прямоугольника. Учащиеся знакомы с прямоугольником еще с начальной школы, поэтому ввести понятие прямоугольника можно в процессе беседы по вопросам: — Какой четырехугольник называется прямоугольником? (Ученики могут дать различные ответы, например: “Это четырехугольник, у которого все углы прямые”; “Это четырехугольник, у которого противолежащие стороны равны”.) — Можно ли утверждать, что прямоугольник — это параллелограмм, и почему? — Чем отличается произвольный параллелограмм от прямоугольника? — Закончите предложение: “Прямоугольник — это параллелограмм, у которого…” — Сформулируйте свойства прямоугольника. (И/Г) 2. Рассмотреть особое свойство диагоналей прямоугольника. — Исследуйте стороны, углы и диагонали прямоугольника и заполните таблицу.
		Параллелограмм	Прямоугольник
Стороны	1. 2.	1. 2.
Углы	1. 2.	1. 2. 3.
Диагонали	1.	1. 2.
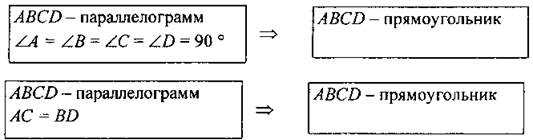
(И/Ф) 3. Рассмотреть признак прямоугольника. — Как определить, является ли данный параллелограмм прямоугольником? Ответ обоснуйте. (Дать учащимся 3-5 минут на обдумывание и обсудить варианты ответов.) (Ф) — Выберите верные утверждения (устно): а) Если в четырехугольнике диагонали равны и делятся точкой пересечения пополам, то этот четырехугольник — прямоугольник. б) Если в четырехугольнике противоположные стороны параллельны, а все его углы прямые, то этот четырехугольник — прямоугольник. в) Если в четырехугольнике диагонали равны, то этот четырехугольник — прямоугольник. г) Если в параллелограмме два угла прямых, то этот параллелограмм — прямоугольник. д) Если в четырехугольнике два прямых угла и две стороны равны, то этот четырехугольник — прямоугольник. е) Если в четырехугольнике диагонали равны, а один угол прямой, то этот четырехугольник — прямоугольник
III этап. Решение задач
Цель деятельности	Деятельность учителя	Деятельность учащихся
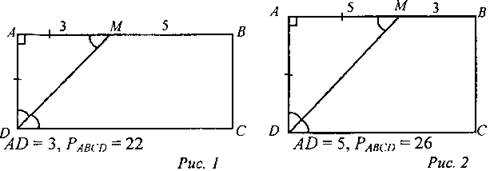
Совершенствовать навыки решения задач, опираясь на полученные знания	(И/Ф)1. Решите задачу: В прямоугольнике ABCD биссектриса угла D пересекает сторону АВ в точке М. Докажите, что ∆ADM — равнобедренный. Найдите периметр прямоугольника, если сторона АВ оказалась разбита на отрезки длиной 3 см и 5 см. Сколько решений имеет задача? 2. Решите № 403. Дано: ABCD — прямоугольник, АС ∩ BD = О, ∠CAD = 30°, АС = 12 см. Найти: РAOB	1. Решение: № 403. Решение: ∆ACD — прямоугольный, в нем ∠CAD = 30°, значит, тогда АВ = CD = 6 см. В прямоугольнике диагонали равны и точкой пересечения делятся пополам, то есть РAOB = АО + ВО + АВ = 6 + 6 + 6 = 18 см. Ответ: РАOB = 18 см
IV этап. Итоги урока. Рефлексия
Деятельность учителя	Деятельность учащихся
(Ф)	(И) Домашнее задание: п. 46 прочитать, решить № 401, 404

ПредыдущаяСледующая

Простейшие виды фигур

Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.

Точка

Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик

Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.

Например, A, B, C или 1, 2, 3.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

Самыми простейшими фигурами являются луч и отрезок.

• Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.
• Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.

Линия

Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными. 

• Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая — когда начало и окончание линии не соединены.
• Прямая — непрерывная линия без изменений.
• Кривая — отличная от прямой линии.
• Ломаная — когда соединены отрезки не под углом 180 градусов. 

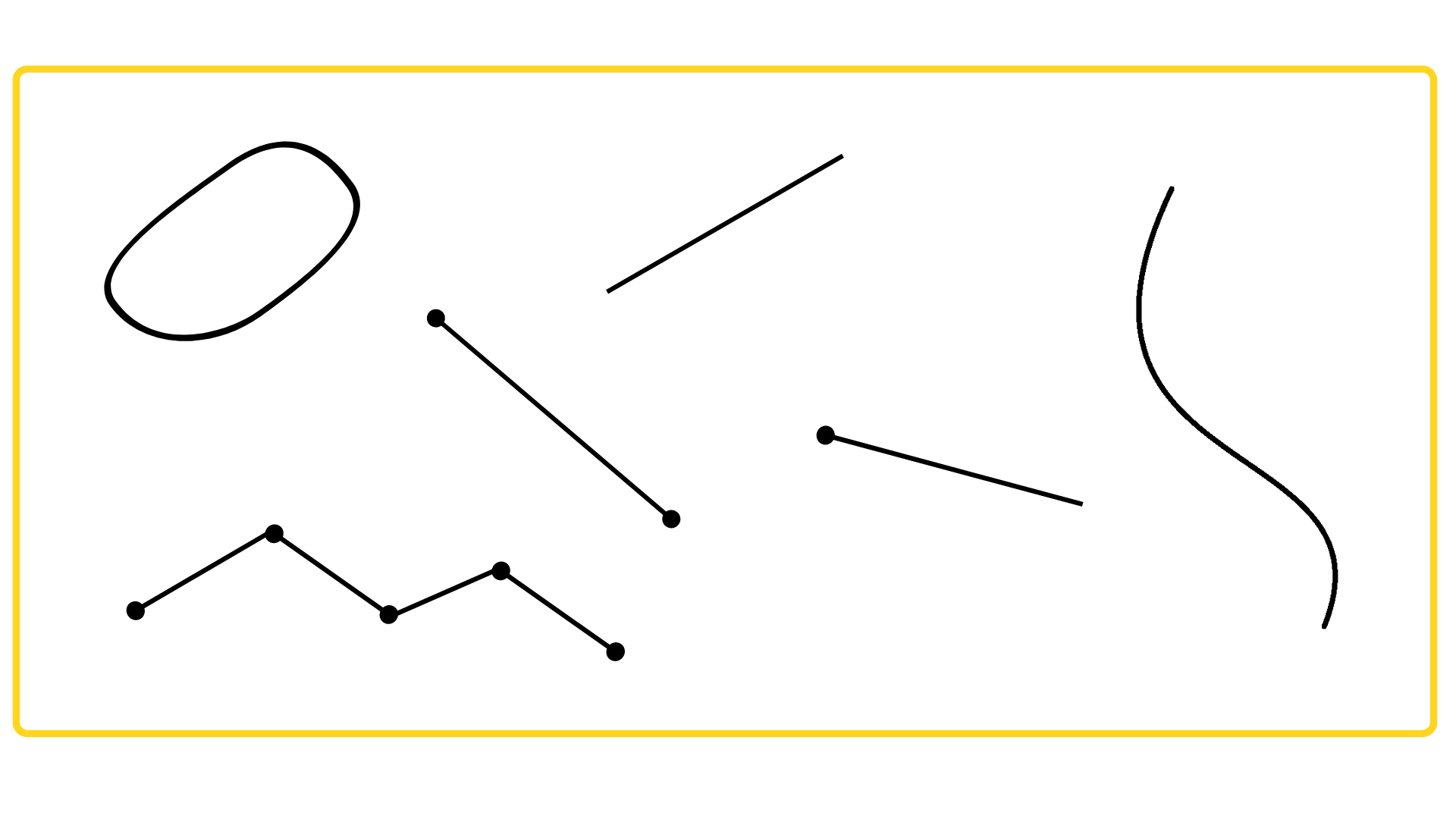
Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.

Четырехугольник

Начнем с так называемой базы. 

Четырехугольник — геометрическая фигура, которая состоит из четырех вершин, которые соединены четырьмя отрезками. 

Важное условие четырехугольника заключается в том, что любые три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются. Мы будем рассматривать выпуклые четырехугольники

Такой четырехугольник расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон

Мы будем рассматривать выпуклые четырехугольники. Такой четырехугольник расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.

Например, вот этот четырехугольник — невыпуклый. 

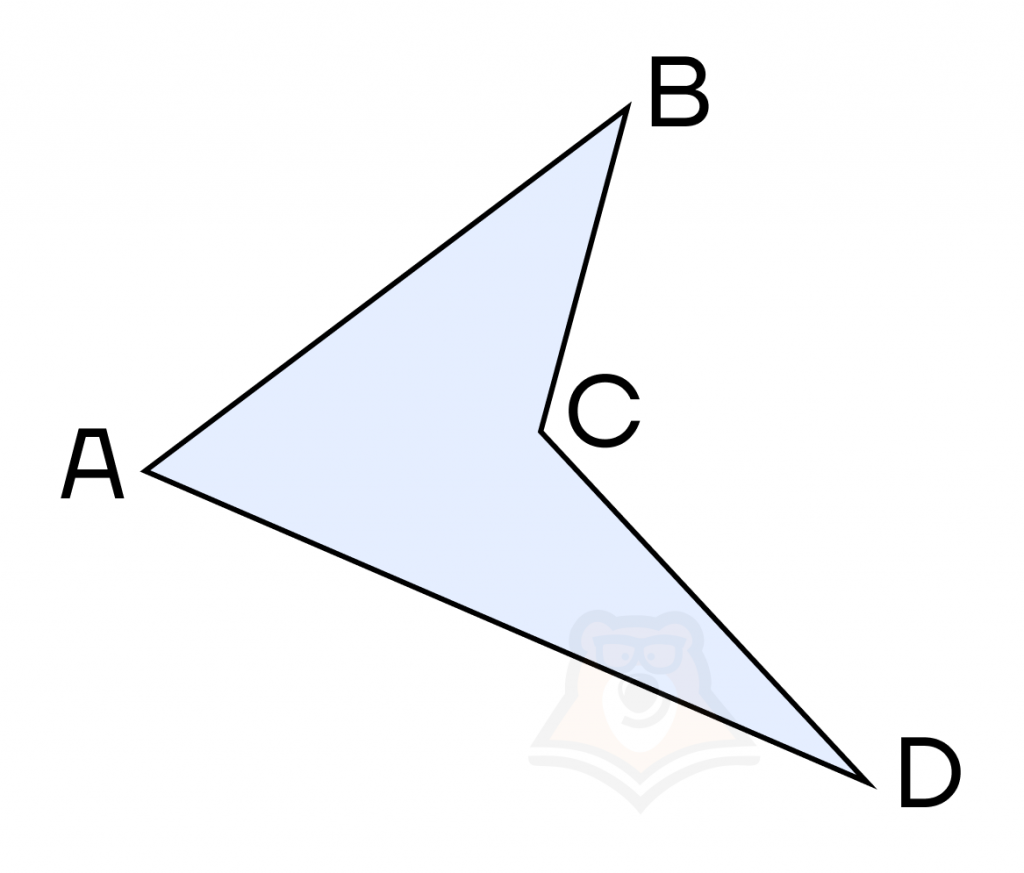
А вот этот — выпуклый. И все четырехугольники, которые мы будем рассматривать дальше, — выпуклые.

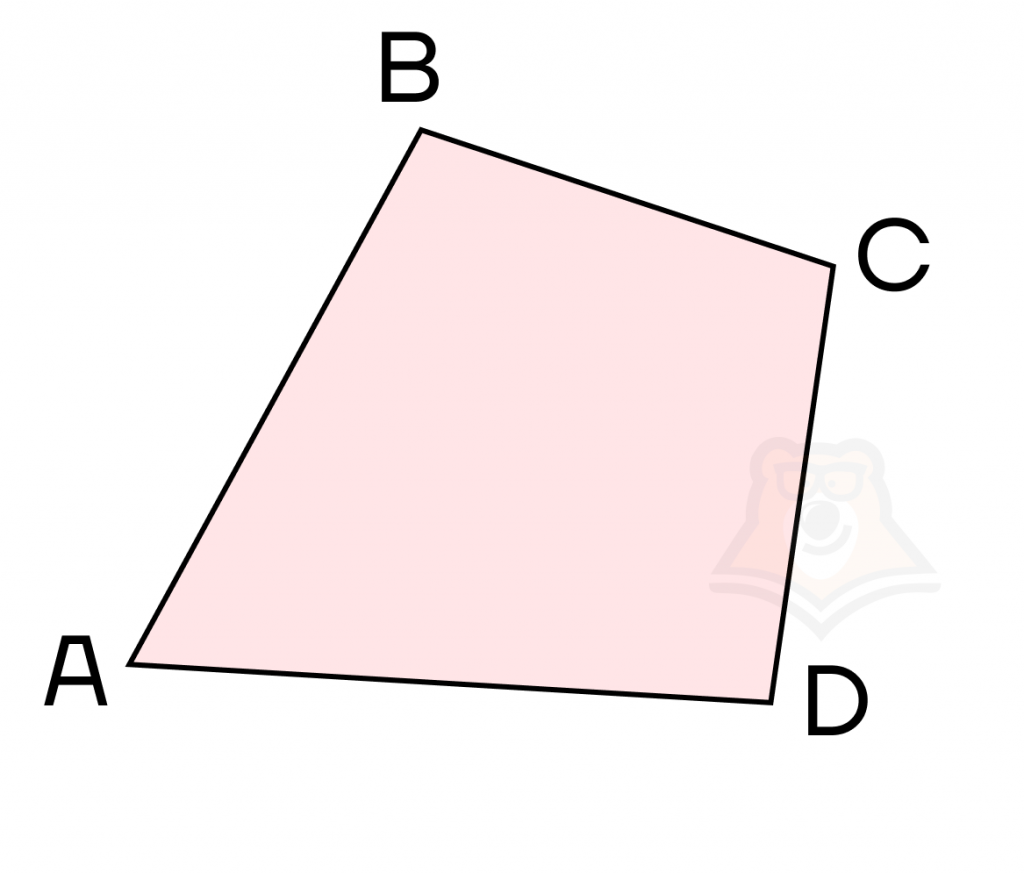
В выпуклом многоугольнике можно посчитать сумму углов по формуле:

\((n-2)*180°\)

Соответственно, для четырехугольника:

\((4-2)*180°=2*180°=360°\)

Итак, теперь мы можем перейти к частным случаям многоугольников.

Свойства четырехугольников. Параллелограмм

Свойства параллелограмма

Внимание! Слова «свойства параллелограмма
» означают, что если у тебя в задаче есть
параллелограмм, то всем нижеследующим можно пользоваться

Теорема о свойствах параллелограмма.

В любом параллелограмме:

Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.

Итак, почему верно 1)?

Раз — параллелограмм, то:

• как накрест лежащие
• как накрест лежащие.

Значит, (по II признаку: и — общая.)

Ну вот, а раз, то и — всё! — доказали.

Но кстати! Мы ещё доказали при этом и 2)!

Почему? Но ведь (смотри на картинку), то есть, а именно потому, что.

Осталось только 3).

Для этого всё-таки придётся провести вторую диагональ.

И теперь видим, что — по II признаку (угла и сторона «между» ними).

Свойства доказали! Перейдём к признакам.

Признаки параллелограмма

Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.

В значках это так:

Почему? Хорошо бы понять, почему — этого хватит. Но смотри:

Ну вот и разобрались, почему признак 1 верен.

Ну, это ещё легче! Снова проведём диагональ.

А значит:

Итоже несложно. Но …по-другому!

Значит, . Ух! Но и — внутренние односторонние при секущей!

Поэтому тот факт, что означает, что.

А если посмотришь с другой стороны, то и — внутренние односторонние при секущей! И поэтому.

Видишь, как здорово?!

И опять просто:

Точно так же, и.

Обрати внимание:
если ты нашел хотя бы
один признак параллелограмма в своей задаче, то у тебя точно
параллелограмм, и ты можешь пользоваться всеми
свойствами параллелограмма. Для полной ясности посмотри на схему:. Для полной ясности посмотри на схему:

Для полной ясности посмотри на схему:

Определение и свойства квадрата

Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.

Четырёхугольник называют квадратом в следующих случаях:

1. Если это прямоугольник, у которого длина a и ширина b равны.
2. Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.

К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:

1. Диагонали перпендикулярны относительно друг друга (свойство ромба).
2. Точка пересечения совпадает с центром вписанной окружности.
3. Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.

Приведём часто используемые формулы для вычисления периметра, площади и элементов квадрата:

• Диагональ d = a √2.
• Периметр P = 4 a.
• Площадь S = a ².
• Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
• Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.

В заключение: геометрия 8 класса и четырехугольники

В 8 классе российских школ особое внимание уделяется геометрии. Изучение четырехугольников играет важную роль в формировании геометрических навыков у учащихся

1. Понимание свойств: В 8 классе ученики углубляются в изучение свойств различных четырехугольников, что помогает им в дальнейшем решать более сложные задачи.
2. Практические задачи: Учащиеся решают разнообразные задачи, связанные с четырехугольниками, что помогает закрепить теоретические знания на практике.
3. Подготовка к ЕГЭ: Знание основных свойств четырехугольников и умение работать с ними – это важная часть подготовки к единому государственному экзамену по математике.

Знание геометрии формирует логическое мышление и аналитические способности, которые пригодятся учащимся в будущем независимо от выбранной ими профессии.