Суть концепции значения измеренной величины
Значение измеренной величины является ключевым понятием в области измерений и метрологии. Оно представляет собой числовое выражение количественной характеристики объекта или явления, полученное в результате измерения. Значение измеренной величины имеет две составляющие: числовую и размерность.
Числовая составляющая определяет количественное значение измеренной величины и выражается числом или числовым выражением. Например, для измерения длины объекта может быть получено значение 10 метров или 1000 миллиметров.
Размерностная составляющая определяет единицы измерения, в которых выражается значение измеренной величины. Размерностная составляющая не является числовой, но важна для определения полной информации об измерении. В примере с длиной объекта, размерность может быть выражена в метрах или миллиметрах.
Значение измеренной величины играет важную роль в научных исследованиях, промышленности, торговле и других областях, где требуется количественная оценка объектов и процессов. Благодаря значению измеренной величины возможна проверка соответствия объектов заданным параметрам, сравнение и анализ данных, установление стандартов и нормативов.
Оценка точности и достоверности значения измеренной величины является важной задачей метрологии. Значение измеренной величины может быть получено с использованием различных методов и приборов, и может содержать погрешности, вызванные неточностью измерительных средств или условиями проведения измерений
Важно проводить калибровку и поверку измерительных приборов, а также анализировать и контролировать погрешности, чтобы получить достоверное значение измеренной величины.
Общий случай: находим значения выражений с дробями, функциями, степенями и не только
Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:
- Степени;
- Скобки;
- Корни;
- Функции и т.д.
Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.
Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:
- Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
- Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
- Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
- Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.
Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.
Задача. Решить:
\
Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:
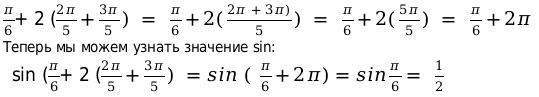
Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:
\
Со знаменателем дела обстоят куда проще:
\
Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:
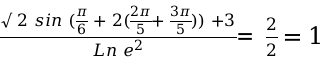
Теперь остается решить следующее выражение:
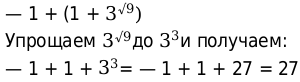
Ответ. 27
Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.
Решаем выражения с тригонометрической функцией
Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:
- Синус;
- Косинус;
- Котангенс;
- Тангенс;
- Секанс;
- Косеканс.
Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.
В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.
Задача. Решить:
\
Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:
sin217 — sin (90 + 127) = cos127
Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:
\
Вспоминаем, что по тригонометрическому тождеству sin2a+ cos2 a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin2127+ cos2127) преобразуем в единицу и получаем:
\
Ответ. 2
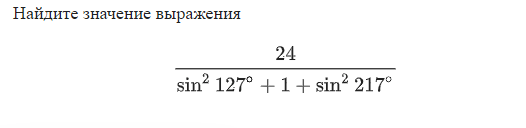
Важно: Не стоит бояться буквенных тригонометрических значений. Большинство примеров построено таким образом, чтобы функции можно было заменить более удобной для вычисления формулой
Поэтому вместо того, чтобы пытаться сразу решить пример, стоит обратить внимание на особенности функций и возможность их приведения к подходящей формуле
Задача. Решить:
\
Решение. Начинаем решение с разбора второй дроби
Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48
Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:
\
Ответ. — 6.
Значение числового выражения с корнями
Задача. Решить:
√ 2² • 2² • 3² = ?
Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:
√2² • √2² • √3² = ?
Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:
2 • 2 • 3 = 12
Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12
Ответ. 12
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Находим значение числовых выражений со степенями
Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.
Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: \), то его необходимо решить в нашем примере это будет: \.
Задача. Решите:
\[
3^{1 / 3} \cdot 7^{1 / 3} \cdot 21^{2 / 3}=?
\]
Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:
\
Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:
\[
(3 \cdot 7)^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3} \cdot 21^{2 / 3}
\]
Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:
\[
21^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21
\]
Решение без пояснений: \[3^{1 / 3} \cdot 7^{1 / 3} \cdot 21^{2 / 3}=(3 \cdot 7)^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3} \cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21\]
Ответ. 21
Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:
\[3^{1 / 3} \cdot 7^{1 / 3} \cdot 21^{2 / 3}=3^{1 / 3} \cdot 7^{1 / 3} \cdot(3 \cdot 7)^{2 / 3}=3^{1 / 3} \cdot 7^{1 / 3} \cdot 3^{2 / 3} \cdot 7^{2 / 3}=3^{1 / 3+2 / 3} \cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21\]
Ответ. 21
Задача. Решить:
\[
2^{-2 \sqrt{5}} \cdot 4^{\sqrt{5}-1}+\left((\sqrt{3})^{1 / 3}\right)^{6}
\]
Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:
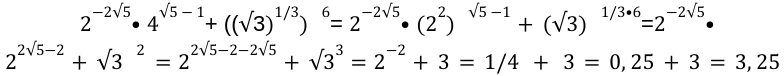
Ответ. 3,25
Выражения с дробями
Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.
Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения
Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.
Задача. Решить:
\
Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:
\
Теперь выполняем вычисления в знаменателе и числителе и находим ответ:
\
Ответ. \
Примеры(2):

Задача. Решить:
\
Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:
\
Теперь можем придать нашему первоначальному выражению следующий вид:
\
Ответ. \.
Выражения с логарифмами
Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что \ мы можем сразу упростить выражение \ до простого и понятного 2 + 5*6 = 32.
Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).
В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.
Задача. Решить:
\
Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:
Это позволит нам решить пример следующим образом:

Ответ. 2




























