Как составить конспект по геометрии 7 класс

Структура конспекта по геометрии

Конспект по геометрии в 7 классе включает основные понятия и термины, которые учащиеся должны изучить в данном курсе. Он помогает систематизировать знания, а также служит вспомогательным материалом для повторения и закрепления изученного материала.

Структура конспекта по геометрии обычно следующая:

1. Основные понятия:
   • Геометрические фигуры — плоские и пространственные фигуры, такие как треугольник, прямоугольник, круг и др.
   • Линии и отрезки — прямая, луч, отрезок, полупрямая.
   • Углы — прямой угол, острый угол, тупой угол, смежные углы.
   • Углы и параллельные прямые — вертикальные углы, односторонние углы, углы с косой.
2. Формулы и свойства:
   • Площадь прямоугольника — S = a * b, где а и b — длины сторон прямоугольника.
   • Площадь треугольника — S = (1/2) * a * h, где a — основание треугольника, h — высота.
   • Теорема Пифагора — a^2 + b^2 = c^2, где a и b — катеты прямоугольного треугольника, c — гипотенуза.
   • Сумма углов треугольника — 180 градусов.
3. Примеры задач:
   

   Задача	Решение
   Найти площадь круга с радиусом 5	Для нахождения площади круга используется формула S = π * r^2, где r — радиус круга. Подставляя значения из условия, получаем: S = π * 5^2 = 25π
   Найти длину окружности с радиусом 3	Для нахождения длины окружности используется формула L = 2πr, где r — радиус окружности. Подставляя значения из условия, получаем: L = 2π * 3 = 6π

Примеры использования ЧТД в геометрии 8 класса

В 8 классе, изучая геометрию, ученики активно применяют ЧТД (четырёхугольник, треугольник, диагонали) для решения задач различной сложности. Вот несколько примеров использования ЧТД в геометрии 8 класса:

Пример 1: Рассмотрим четырёхугольник ABCD, в котором известны стороны AB, BC, CD и угол BCD. С помощью ЧТД можно найти длину диагонали AC. Для этого можно воспользоваться теоремой косинусов и формулой для диагоналей в четырёхугольнике.

Пример 2: Пусть дан треугольник ABC, в котором известны стороны AB, BC и AC. С помощью ЧТД можно найти высоты треугольника, проведённые из вершин A, B и C. Это позволит решить задачу на нахождение площади треугольника или найти длину отрезка между параллельными прямыми.

Пример 3: Рассмотрим четырёхугольник ABCD, в котором известны длины диагоналей AC и BD. С помощью ЧТД можно найти длины сторон и углы между этими сторонами. Определение этих параметров позволит решить различные задачи, например, найти площадь четырёхугольника или найти длину перпендикуляра, опущенного из точки пересечения диагоналей, на одну из сторон четырёхугольника.

Таким образом, применение ЧТД в геометрии 8 класса позволяет решать разнообразные задачи на нахождение длин сторон и диагоналей фигур, нахождение площадей и углов, а также определение других геометрических параметров. Отличное знание ЧТД поможет ученикам успешно справиться с геометрическими задачами и развить свои навыки в этой области.

Аксиома разбиения (дополнительная)

Интуитивно эта аксиома вполне очевидна. Если две точки лежат по разные стороны от плоскости $\alpha $, то отрезок, соединяющий эти точки, неизбежно пересечёт плоскость $\alpha $. И наоборот: если точки лежат по одну сторону от плоскости $\alpha $, то отрезок, их соединяющий, не пересечёт эту плоскость.

На рисунке мы видим, что отрезок $AB$ пересекает плоскость $\alpha $ в точке $M$, поскольку точки $A$ и $B$ лежат по разные стороны от $\alpha $. И наоборот: отрезок $AC$ не пересекает плоскость $\alpha $, поскольку точки $A$ и $C$ лежат по одну сторону от плоскости.

Здесь можно долго рассуждать, что плоскость $\alpha $ делит всё пространство на два полупространства. Что эта плоскость является границей для таких полупространств. Но это уже аналитическая геометрия и топология — сейчас не будем залезать в дебри.

Основные понятия

В планиметрии, которая является разделом геометрии, изучаются различные фигуры и их свойства на плоскости. Учебный курс планиметрии в 7 классе включает в себя основные понятия и термины, с которыми необходимо ознакомиться для успешного изучения предмета.

Основные понятия планиметрии включают в себя:

• Фигуры: в планиметрии изучаются различные геометрические фигуры, такие как треугольники, квадраты, прямоугольники, круги и др. Каждая фигура имеет свои уникальные свойства и характеристики.
• Отрезок: это часть прямой, которая ограничена двумя точками.
• Угол: это область плоскости между двумя лучами, имеющими общее начало.
• Параллельные прямые: прямые, которые не пересекаются и находятся на одной плоскости.
• Перпендикулярные прямые: прямые, которые пересекаются и образуют прямой угол.

Важным понятием в планиметрии также является понятие площади. Площадь — это мера двумерной поверхности, занимаемой фигурой. Для различных фигур существуют формулы для вычисления площади.

Помимо вышеуказанных понятий, на уроках планиметрии в 7 классе изучаются и другие термины и свойства геометрических фигур, такие как диагональ, радиус, теоремы и правила.

ЧТД в геометрии 8 класс

Четырехугольники являются многоугольниками с четырьмя сторонами. Они могут быть выпуклыми или невыпуклыми, ромбами, прямоугольниками, квадратами, параллелограммами и т.д

Важно уметь определять тип четырехугольника по его свойствам и знать основные формулы для вычисления его периметра и площади

На уроках геометрии 8 класса ученики также изучают различные теоремы о четырехугольниках, например, теорему о сумме углов в четырехугольнике или теорему о параллельности диагоналей в параллелограмме. Эти теоремы позволяют решать различные задачи на построение и вычисление параметров четырехугольников.

Важно помнить, что изучение четырехугольников в 8 классе является основой для дальнейшего изучения геометрии, поэтому рекомендуется усвоить материал тщательно и попрактиковаться в решении задач

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника. Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет

Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Сумма любых двух сторон треугольника больше его третьей стороны.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

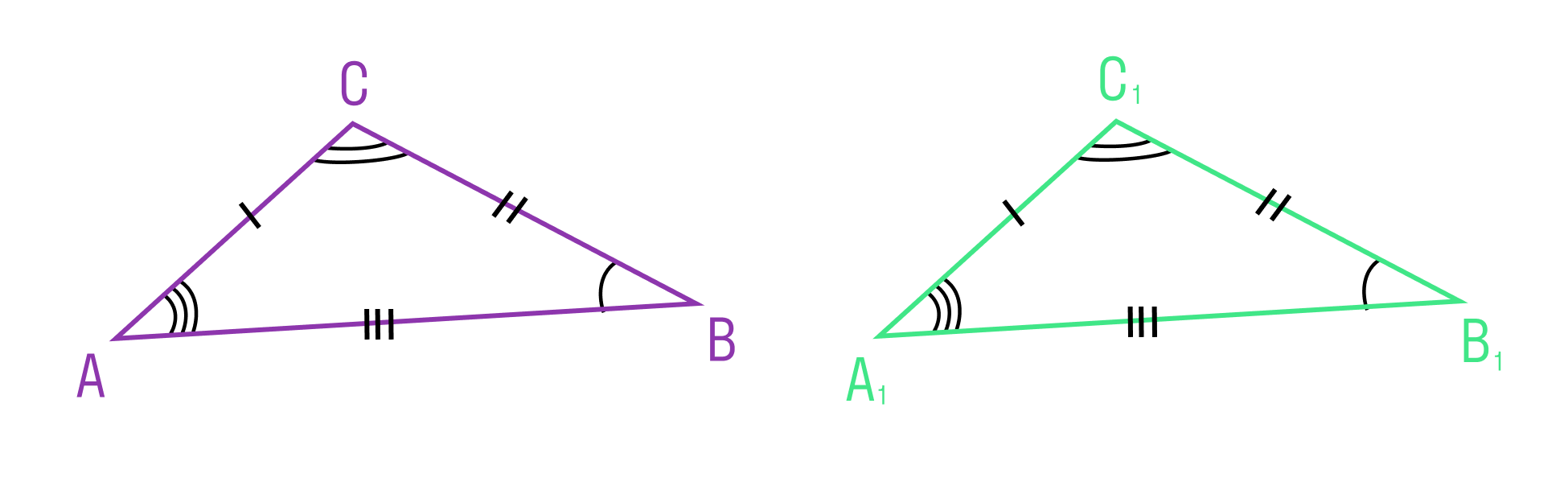
Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

Первый признак равенства треугольников звучит так:

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

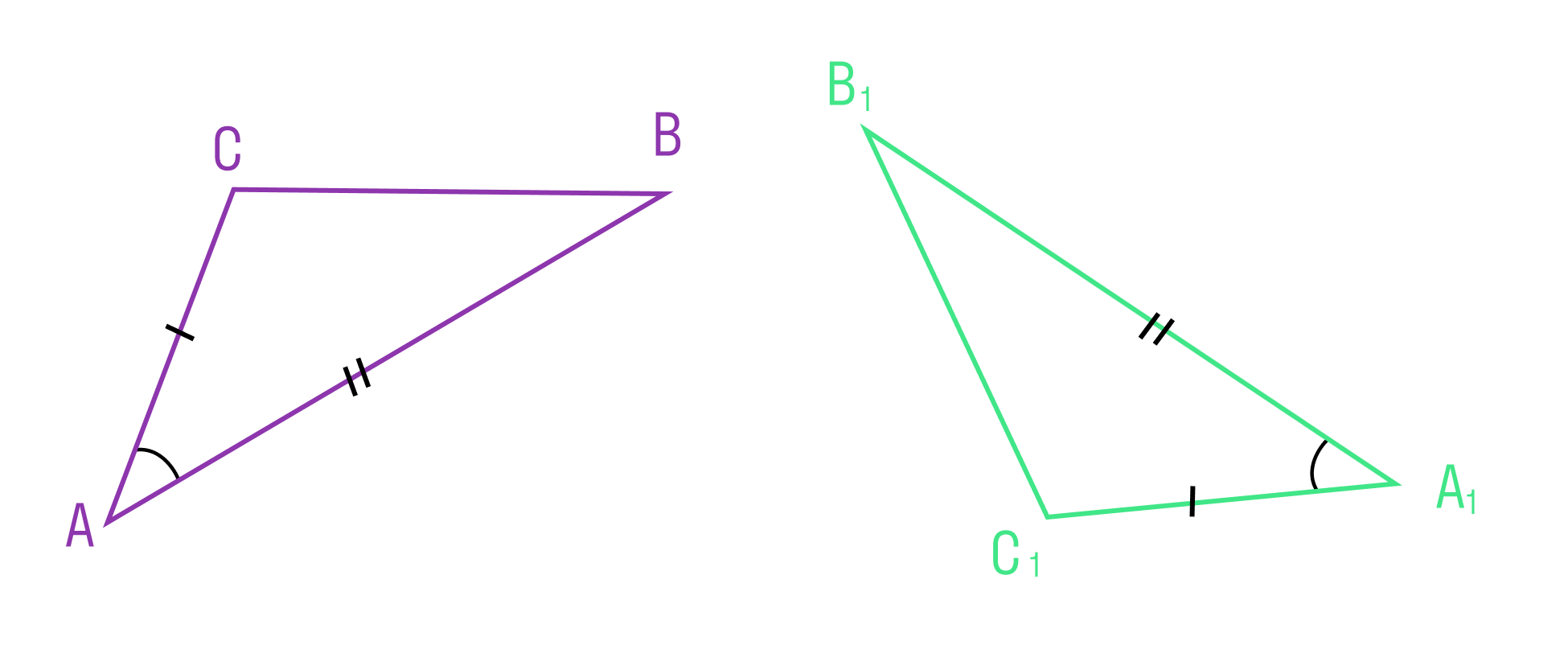
Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

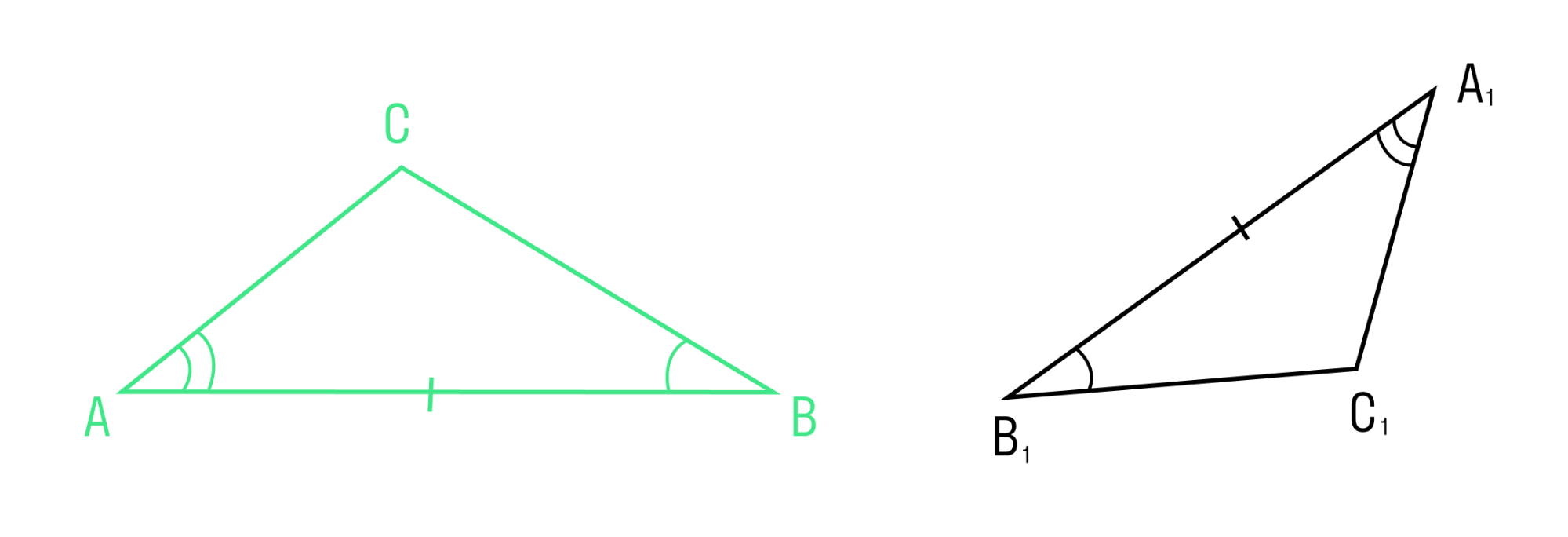
Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

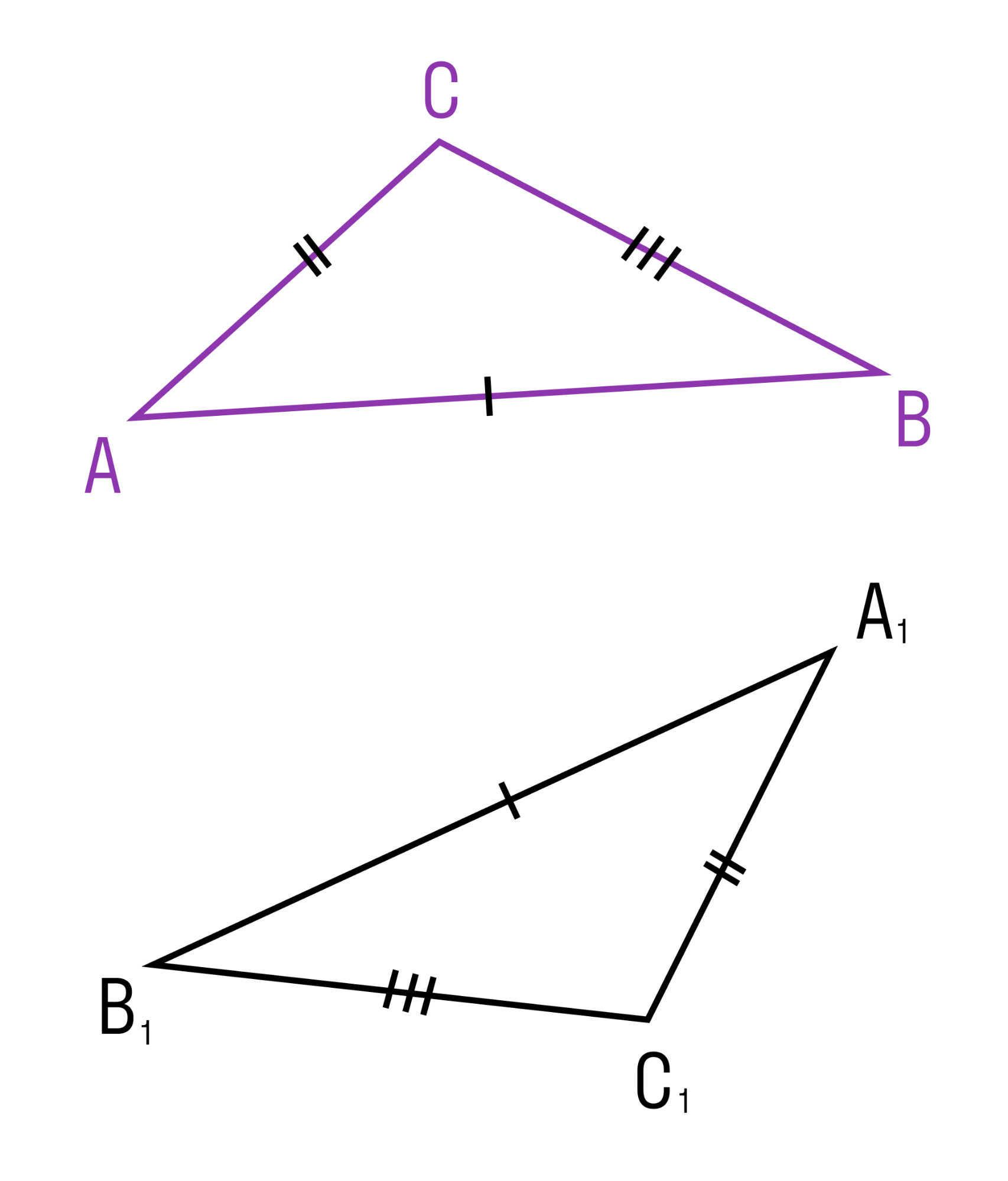
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Будущее ЧТД в геометрии 7 класс

Развитие технологий и доступность компьютеров и интернета открывает новые возможности для применения ЧТД в геометрии. Современные программы и онлайн-ресурсы позволяют использовать геометрические построения и вычисления для решения задач с помощью ЧТД.

Одним из примеров будущего ЧТД в геометрии 7 класса является разработка интерактивных учебных материалов и приложений, которые позволяют ученикам активно взаимодействовать с геометрическими объектами и находить аналитическое решение задач с помощью ЧТД. Такие инструменты могут сделать процесс обучения геометрии более интересным и понятным.

Будущее ЧТД в геометрии 7 класса также может связываться с развитием компьютерных алгоритмов и программ, которые будут автоматически находить ЧТД-решение для конкретной задачи. Это позволит ученикам сосредоточиться на развитии аналитического мышления и применении математических знаний, а не тратить время на рутинные вычисления.

Однако несмотря на развитие технологий, понимание и применение ЧТД в геометрии остается важным навыком для учащихся 7 класса. ЧТД развивает логическое мышление, способность анализировать геометрические свойства и делать выводы. Правильное применение ЧТД помогает решать сложные задачи и находить эффективные пути решения.

Критерии оценивания

Сочинение оценивается по пяти критериям, по каждому можно получить или зачет или незачет. Первые два критерия самые важные: если не получить по ним зачет, экзамен провален. Чтобы получить зачет за сочинение в целом, нужно справиться с первыми двумя критериями и еще хотя бы одним.

2. Привлечение литературного материала

Чтобы получить зачет, нужно привести минимум один литературный аргумент — из русской классики, школьной программы или мировой литературы. Можно использовать даже «Гарри Поттера» или «Голодные игры». Главное — написать развернутый аргумент, который подтвердит ваше мнение.

3. Композиция и логика рассуждения

Чтобы получить балл по этому критерию, предлагаем использовать классическую структуру сочинения.

 5 абзацев

• вступление (тезис),
• собственное мнение, которое доказывается аргументами,
• аргумент 1 (доказательство и микровывод),
• аргумент 2 (доказательство или контраргумент + микровывод),
• вывод (итог рассуждений).

Если сочинение выстроено логично и в нем есть абзацное членение, то данный критерий засчитают.

5. Грамотность

Незачет поставят, если на 100 слов приходится в сумме более пяти ошибок: грамматических, орфографических, пунктуационных. Помните, что на сочинении можно пользоваться орфографическим словарем! Этот поможет свести орфографические ошибки к минимуму.

Что такое конспект по геометрии 7 класс

Конспект по геометрии в 7 классе – это систематизированный материал, который помогает ученикам лучше понять и запомнить основные понятия и принципы данного предмета. Он представляет собой краткую и структурированную запись учебного материала, включающую в себя определения, теоремы, примеры и упражнения.

В конспекте по геометрии 7 класса присутствуют следующие основные принципы:

Определения. В конспекте перечисляются основные понятия и вводятся их определения, которые помогают понять суть предмета.
Теоремы

В конспекте приводятся основные теоремы и правила геометрии, которые ученику важно знать и уметь применять.
Примеры. Конспект содержит примеры решения задач и применения теорем, которые помогают ученику лучше усвоить материал и освоить методики решения.
Упражнения

В конспекте могут быть предложены упражнения, которые позволяют ученику отработать пройденный материал и проверить свои знания.

Конспект по геометрии 7 класса имеет ряд преимуществ. Во-первых, он помогает ученикам систематизировать и организовать знания, полученные во время изучения предмета. Во-вторых, конспект позволяет быстро и легко повторить материал перед контрольной работой или экзаменом. В-третьих, конспект может служить вспомогательным материалом для самостоятельной подготовки ученика.

В итоге, конспект по геометрии 7 класса является незаменимым инструментом для более глубокого и качественного усвоения предмета. Хорошо составленный и структурированный конспект помогает ученикам лучше понять материал, усвоить важные понятия и научиться применять их на практике.

Кому могут пригодиться ГДЗ Атанасяна?

В 7-9 классах ученик должен выполнять домашнюю работу самостоятельно. Да и не каждый родитель сможет вспомнить пройденное когда-то давно в школе, да еще и по такому сложному предмету как геометрия. На выручку придет онлайн решебник к учебнику Атанасяна Л.С. по геометрии за 7-9 классы, содержащий детальные ответы и развернутые комментарии к каждому упражнению. Использование пособия гарантирует:

1. Правильное выполнение домашних заданий.
2. Возможность самостоятельной проработки тем наперед, повторения пройденного материала или восполнения пропущенного.
3. Эффективную подготовку к ответу у доски или написанию контрольной работы.
4. Отсутствие необходимости посещения репетитора (возможность сэкономить время и семейный бюджет).

Объем новой информации в старших классах становится все больше год от года. Усвоить и понять материал на уроке не всегда могут даже ученики с хорошей успеваемостью. Подробные алгоритмы, приведенные в ГДЗ по геометрии 7-9 класс, станут незаменимым помощником дома.

Простейшие следствия из аксиом стереометрии

На основе аксиом можно доказать несколько простых теорем стереометрии.

Доказательство. Возьмем произвольную прямую m и точку C, которая НЕ принадлежит m. Далее отметим на m две любые точки и обозначим их как А и В:

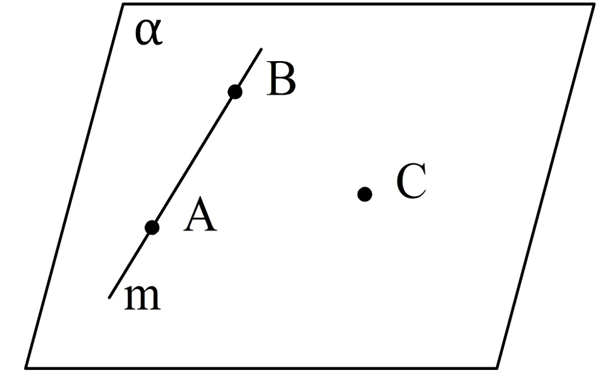
По аксиоме 1 через А, В, С можно провести некоторую плос-ть α. По аксиоме 4 прямая m будет принадлежать α. Тем самым мы показали, что существует плос-ть, проходящая через m и C. Единственность этой плос-ти вытекает уже из аксиомы 2, ведь через А, В и С нельзя провести две различных плос-ти, ч. т. д.

Иногда доказанный факт формулируют иначе: прямая и точка, не находящаяся на прямой, однозначно определяют проходящую через них плос-ть. То есть, указав прямую и точку, можно одновременно указать на ту плос-ть, которая задается ими.

Переходим к следующей теореме.

Отметим на произвольной прямой m точки А и В. Далее выберем ещё две точки в пространстве C и D, причем такие, что А, В, С и D не находятся в одной плос-ти. Тогда у нас есть плос-ти АВС и АВD, которые пересекаются по прямой АВ:

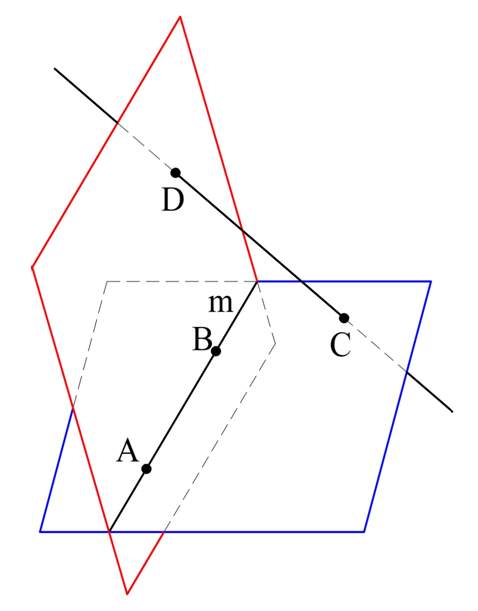
Теперь соединим С и D прямой. Прямая CD состоит из бесконечного количества точек. Через каждую из них можно провести единственную плос-ть, которая будет проходить через АВ. Так как точек бесконечно много, то и плос-тей будет бесконечно много. Осталось лишь показать, что никакие две таких плос-ти не будут совпадать, то есть все они различны.

Действительно, пусть две таких плос-ти совпадают, то есть на самом деле являются одной плос-тью. Тогда получается, что эта единая плоскость проходит через две точки прямой СD. Тогда, по аксиоме 4, вся прямая СD принадлежит этой плос-ти, в том числе и сами точки С и D. Но плос-ть проходит также через А и В. То есть получится, что А, В, С и D входят в состав одной плос-ти, а это не так. Это противоречие означает, что на самом деле все плоскости, проходящие через разные точки прямой CD, будут различны, ч. т. д.

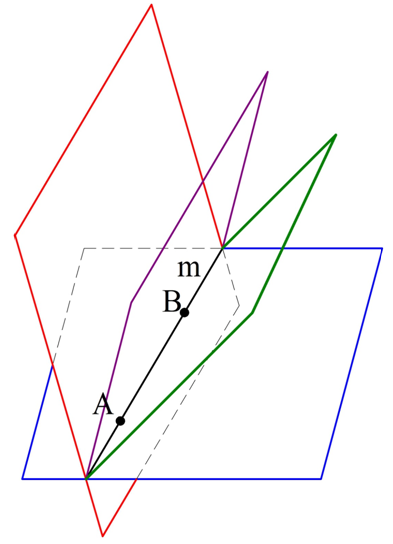
Рассмотрим ещё одну теорему:

Пусть пересекаются прямые m и n. Обозначим точку их пересечения как А. Также выберем на m некоторую точку В, а на n – точку C. Мы можем построить плос-ть α через точки А, В и C, и она будет единственной. Так как и А, и В принадлежат α, то и вся прямая m ей принадлежит (аксиома 4). Аналогично и прямая n находится на плос-ти α. То есть α как раз и является плос-тью, о которой говорится в теореме. Никакая другая плос-ть не будет содержать обе прямые m и n, ведь в противном случае она проходила бы через точки А, В и С, то есть совпадала бы с α.

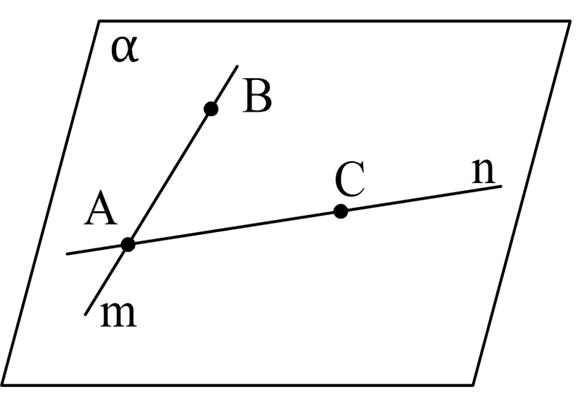
Эта теорема также говорит о том, что две пересекающиеся прямые однозначно определяют проходящую через них плос-ть.

Аксиома прямой и плоскости (основная)

Это интуитивно понятное утверждение, но его нельзя вывести из предыдущих аксиом.

Итак, есть прямая, две точки которой лежат на плоскости:

Следовательно, вся прямая лежит на этой плоскости:

Записывается это так: если точки $\color{red}{A}\in \alpha $ и $\color{red}{B}\in \alpha $, то прямая $l\in \alpha $. Хотя в некоторых учебниках с более строгим изложением предлагают писать $l\subset \alpha $, где знак $\subset $ означает «включение». При этом говорят, что прямая $l$ является подмножеством плоскости $\alpha $.

В этом уроке мы не будем давать строгие теоретико-множественные определения. Потому что сейчас наша цель — максимальная наглядность, а не научная красота. Кому интересно, см. учебник «Геометрия 10» Потоскуева и Звавича.

Вообще существует три варианта взаимного расположения прямой и плоскости в пространстве:

1. Прямая принадлежит плоскости — как раз этот вариант описывает аксиома.
2. Прямая параллельна плоскости, т.е. не имеет с ней общих точек.
3. Прямая пересекает плоскость, т.е. имеет с ней ровно в одну общую точку.

Простой пример: на столе, выполняющем роль плоскости $\alpha $, стоит кирпич $ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$.

Прямая $\color{red}{AB}$ лежит в плоскости $\alpha $. Прямая $\color{red}{B{{B}_{1}}}$ пересекает эту плоскость в точке $\color{red}{B}$ (и тут удобна теоретико-множественная запись $\color{red}{B{{B}_{1}}}\cap \alpha =\color{red}{B}$). Наконец, прямая $\color{red}{{{A}_{1}}{{D}_{1}}}$ параллельна плоскости $\alpha $ (пишут $\color{red}{A{{A}_{1}}}\parallel \alpha $).

Основные понятия стереометрии

Стереометрия оперирует всеми теми понятиями, которые нам известны из планиметрии – точка, прямая, окружность, треугольник и т. д. Но помимо них добавляются и иные термины.

Важнейшее из основных понятий стереометрии – это плоскость. Иногда в литературе применяется сокращение плос-ть. Строгого определения плоскости в рамках геометрии не дают, это понятие считается исходным, как понятия точки или прямой в планиметрии. Лишь некоторые ее свойства косвенно указываются с помощью аксиом. В реальной жизни примерами плоскости являются поверхность стола или лист бумаги. Однако, в отличие от них, плоскость не имеет границы, она бесконечна (как и прямая). Плоскость не имеет кривизны, поэтому, например, поверхность шара плоскостью не является. При изображении плоскости на чертежах ее обычно показывают в виде параллелограмма, при этом традиционно их обозначают маленькими буквами греческого алфавита, которые в планиметрии используются для обозначения углов (α, β, γ и т. п. ):

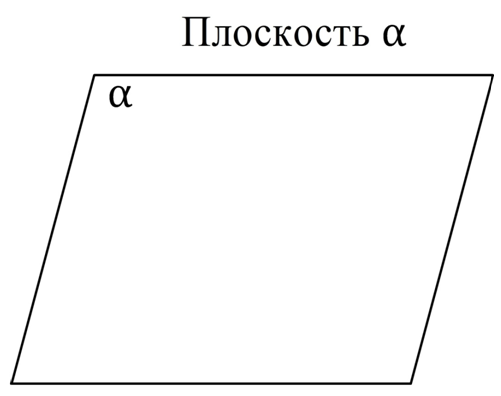
Если на плоскости проведена прямая, то она разобьет ее на две фигуры, которые именуются полуплоскостями:

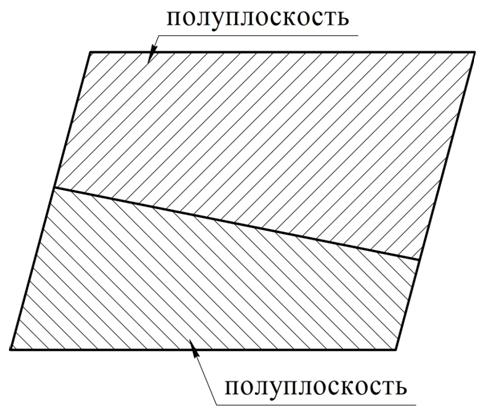
Объемные фигуры – это часть пространства, которая отделена от остального пространства замкнутой поверхностью, то есть границей. Простейший пример объемной фигуры – это куб:

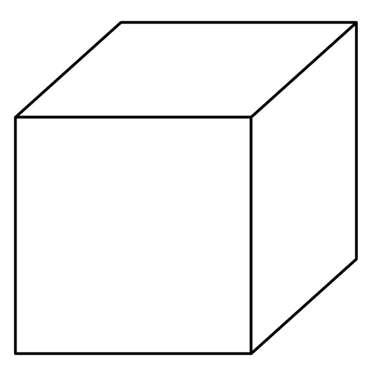
Поверхность куба – это 6 равных квадратов, каждый из них именуется гранью куба. Стороны этих квадратов – это уже ребра куба, а вершины квадратов одновременно являются и вершинами кубов.

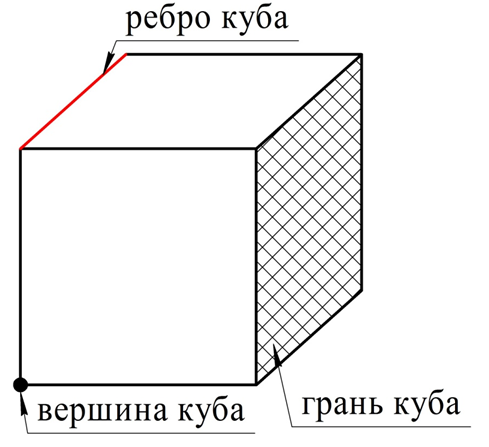
Обратите внимание на изображение куба. Здесь он показан немного сбоку, в результате чего изображение становится объемным

Однако при этом мы вынуждены искажать некоторые размеры и углы на чертеже. Например, верхняя грань должна быть квадратом, но на плоском рисунке углы у этой грани прямыми не являются. При необходимости мы просто ставим специальный значок перпендикулярности между отрезками, который использовали и в планиметрии:

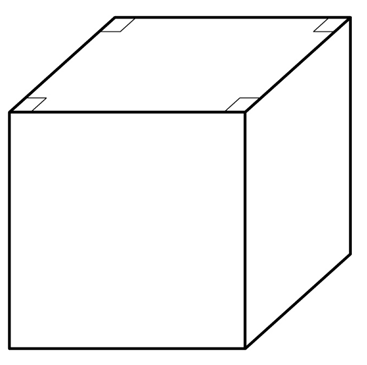
Важно понимать, что из-за искажения размеров у объемных фигур на плоских чертежах мы НЕ можем проверить решение некоторых стереометрических задач с помощью точных построений. Однако есть специальные компьютерные программы 3-D черчения, в которых такие построения уже можно выполнить

Также заметим, что на рисунке видны не все 6 граней куба, а только 3 из них. Если возникает необходимость показать невидимые на чертеже линии, то использует штриховые линии:

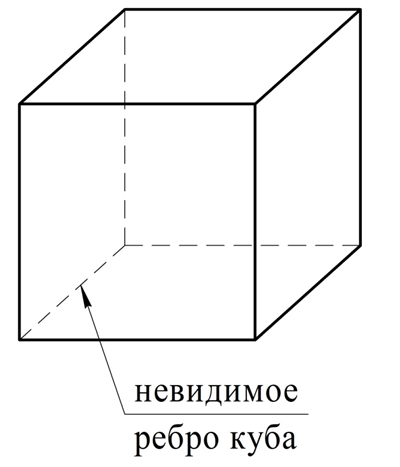
Все грани куба – это многоугольники. Если у фигуры вся ее поверхность состоит лишь из многоугольников, то она именуется многогранником. Таким образом, куб является примером многогранника. Другими примерами многогранников могут служить параллелепипед, пирамида, усеченная пирамида:

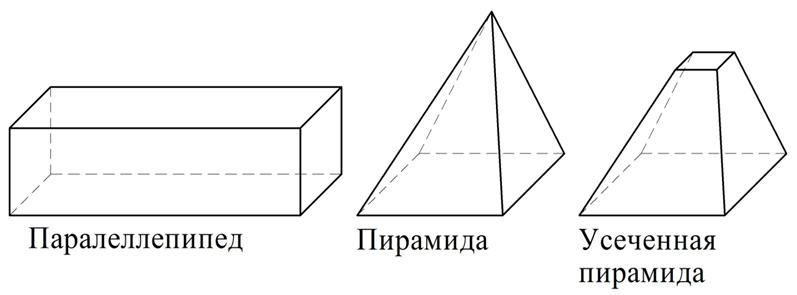
Более подробно различные виды многогранников будут рассматриваться позднее, тогда же им будут даны и их определения.

Если у объемной фигуры хоть одна поверхность не является многоугольником, то она не может считаться многогранником. Наиболее простыми и часто встречающимися такими фигурами являются шар, цилиндр, конус

Обратите внимание, что у них могут отсутствовать ребра и вершины, которые обязательно есть у многогранника:

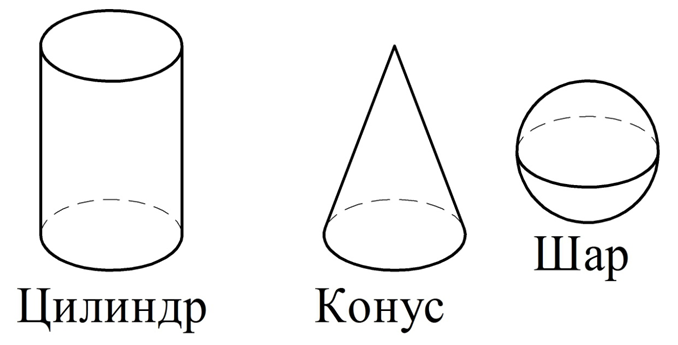
Следует различать саму объемную фигуру и ее границу. Так, шар – это объемная фигура, а поверхность шара – это сфера.

Рекомендации по использованию ЧТД в изучении геометрии школьной программы

Для более глубокого понимания геометрии и умения работать с ЧТД, рекомендуется следующее:

1.
Понять определение и свойства ЧТД. Внимательно изучить определения и основные свойства четырехугольников, треугольников и других фигур. Запомнить основные теоремы и формулировки, чтобы уметь применять их в решении задач.
2.
Решать разнообразные задачи. Регулярно решать задачи, связанные с ЧТД, из учебника и дополнительных источников

Обратите внимание на различные типы задач, чтобы развить умение применять полученные знания в практических ситуациях.
3.
Искать связи с другими разделами геометрии. Выявлять связи между изучаемыми фигурами и другими разделами геометрии, такими как геометрические преобразования, круги и окружности, треугольники и др

Понимание этих связей поможет более глубоко понять геометрию и успешно решать задачи.
4.
Использовать геометрические конструкции. Уметь строить различные геометрические конструкции, связанные с ЧТД, с использованием линейки и циркуля. Это поможет визуализировать задачу и лучше понять ее сущность.
5.
Обращаться за помощью. В случае затруднений не стесняйтесь обращаться за помощью к учителю или одноклассникам. Обсуждение и совместное решение задач поможет лучше усвоить материал и развить навыки решения геометрических задач.
6.
Практиковаться. Регулярная практика поможет закрепить полученные знания и навыки. Решайте задачи как на уроках, так и самостоятельно, чтобы стать более уверенным в решении геометрических задач.

Соблюдение данных рекомендаций поможет учащимся успешно изучить геометрию школьной программы и лучше понять понятие ЧТД, его свойства и применение в задачах.

ЧТД в геометрии 8 класс Атанасян: основная концепция и применение

Концепция ЧТД заключается в следующем: если известно, что прямая проходит через точку некоторой фигуры, то можно извлечь определенные свойства этой точки и применить их для решения геометрических задач.

Одним из наиболее часто используемых применений ЧТД является определение углов. Если прямая проходит через вершину угла, то можно использовать свойства этой прямой и точки для определения значений мер угла.

Применение ЧТД также позволяет решать задачи нахождения длин отрезков. Если известно, что точка лежит на прямой, то можно использовать свойства этой точки и прямой для нахождения длин смежных отрезков.

Для лучшего понимания и применения ЧТД, учебник Атанасян предлагает ряд теоретических материалов, примеров и задач, также предлагает алгоритмы и решения с подробными пояснениями.

ЧТД в геометрии 8 класс Атанасян является важным инструментом для анализа и решения геометрических задач, и его понимание и применение являются необходимыми навыками для успешного изучения геометрии на этом уровне.

Аксиома разбиения (дополнительная)

Интуитивно эта аксиома вполне очевидна. Если две точки лежат по разные стороны от плоскости $\alpha $, то отрезок, соединяющий эти точки, неизбежно пересечёт плоскость $\alpha $. И наоборот: если точки лежат по одну сторону от плоскости $\alpha $, то отрезок, их соединяющий, не пересечёт эту плоскость.

На рисунке мы видим, что отрезок $AB$ пересекает плоскость $\alpha $ в точке $M$, поскольку точки $A$ и $B$ лежат по разные стороны от $\alpha $. И наоборот: отрезок $AC$ не пересекает плоскость $\alpha $, поскольку точки $A$ и $C$ лежат по одну сторону от плоскости.

Здесь можно долго рассуждать, что плоскость $\alpha $ делит всё пространство на два полупространства. Что эта плоскость является границей для таких полупространств. Но это уже аналитическая геометрия и топология — сейчас не будем залезать в дебри.

Аксиома плоскости (основная)

Другими словами, три точки, не лежащие на одной прямой, однозначно определяют плоскость:

На рисунке точки $A$, $B$ и $C$ лежат на плоскости $\alpha $. Поскольку эти точки не лежат на одной прямой, они однозначно задают эту плоскость. Обычно её так и обозначают: плоскость $ABC$.

Простой пример из жизни — стул на трёх ножках. Такого количества опор достаточно, чтобы он не качался и не падал. Плоскость стула задаётся однозначно благодаря всего трём точкам опоры.

Мы будем постоянно использовать эту аксиому для доказательства и решения задач. Ведь если удастся задать плоскость, то мы сведём трёхмерную задачу к двухмерной. А это радикально упрощает рассуждения.

Принципы геометрии 7 класса

1. Принцип соответствия

Принцип соответствия гласит, что фигуры, которые могут быть совмещены без вращения или искажения, считаются равными. Это значит, что две фигуры с одинаковыми размерами и формами считаются равными. Принцип соответствия является основой для различных методов сравнения фигур и решения геометрических задач.

2. Принцип вложения

Принцип вложения гласит, что если фигура целиком содержится внутри другой фигуры, то она также содержится внутри любой другой фигуры, вмещающей первую фигуру. Этот принцип позволяет определять взаимные положения фигур и решать задачи на вложение и пересечение фигур.

3. Принцип сравнения

Принцип сравнения гласит, что сравнение фигур осуществляется путем сравнения их длин, площадей, объемов и других характеристик. Сравнение фигур позволяет устанавливать иерархию между ними и определять отношения между их характеристиками.

4. Принцип построения

Принцип построения гласит, что для решения геометрической задачи необходимо построить определенные фигуры или чертежи, которые позволяют увидеть свойства и зависимости между элементами задачи. Построение фигур помогает визуализировать геометрические задачи и находить ответы на них.

5. Принцип определенности

Принцип определенности гласит, что для каждого геометрического понятия должны быть четкие и однозначные определения. Определения позволяют понять суть геометрического понятия и использовать его в решении задач. Принцип определенности также устанавливает связь между геометрическими понятиями и математическими символами и операциями.

Принципы геометрии 7 класса
Принцип
Описание

Принцип соответствия
Фигуры, совмещаемые без вращения или искажения, считаются равными.

Принцип вложения
Фигура, содержащаяся внутри другой фигуры, содержится и внутри вмещающей фигуры.

Принцип сравнения
Сравнение фигур осуществляется путем сравнения их характеристик.

Принцип построения
Для решения задачи необходимо построить фигуры или чертежи, отображающие свойства и зависимости между элементами.

Принцип определенности
Для каждого геометрического понятия должно быть четкое и однозначное определение.

Взаимодействие объектов

Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.

Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.

Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.

На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.

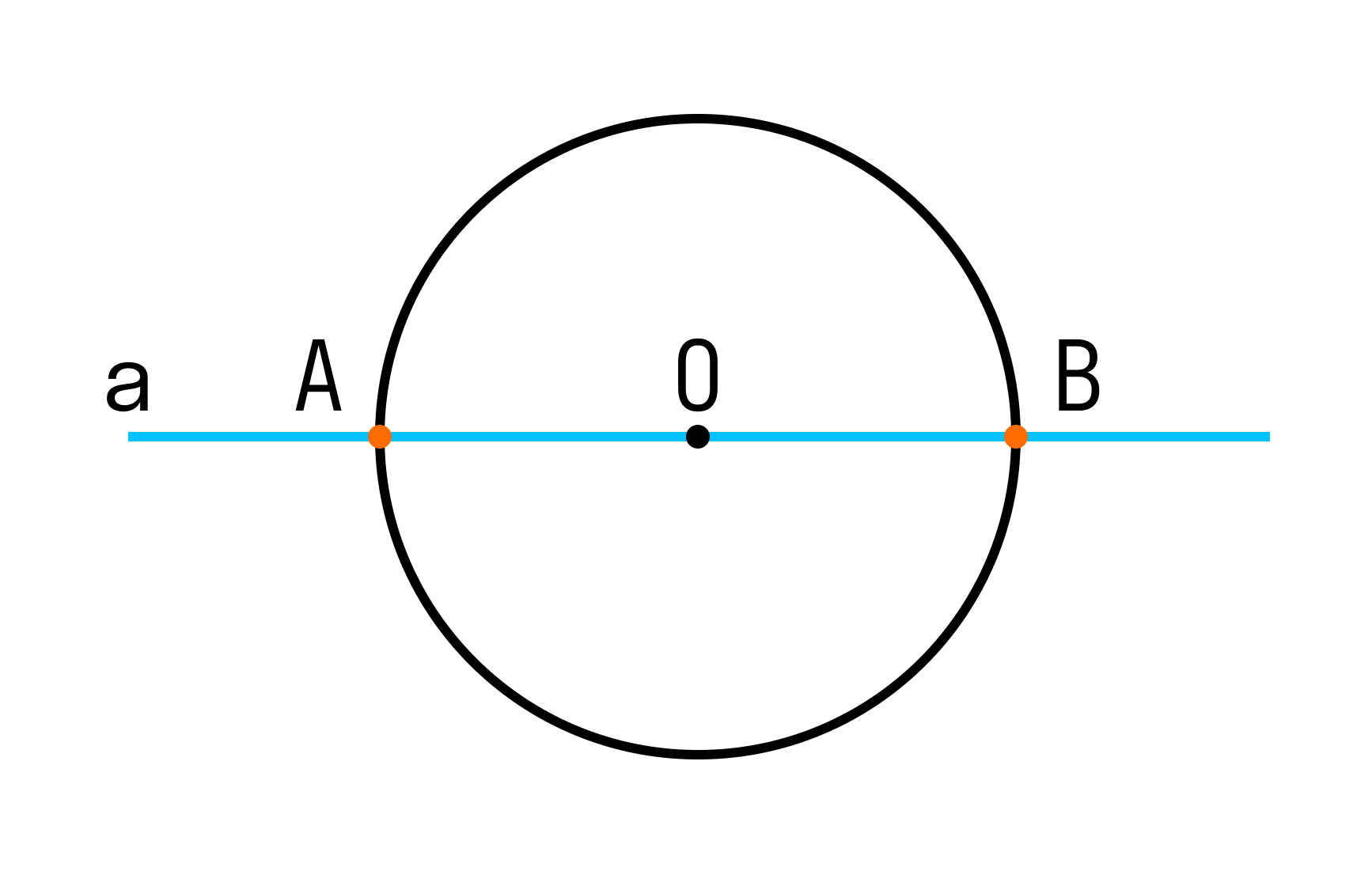
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:

Если расстояние от центра окружности до прямой меньше радиуса окружности (d r), то прямая и окружность не имеют общих точек.

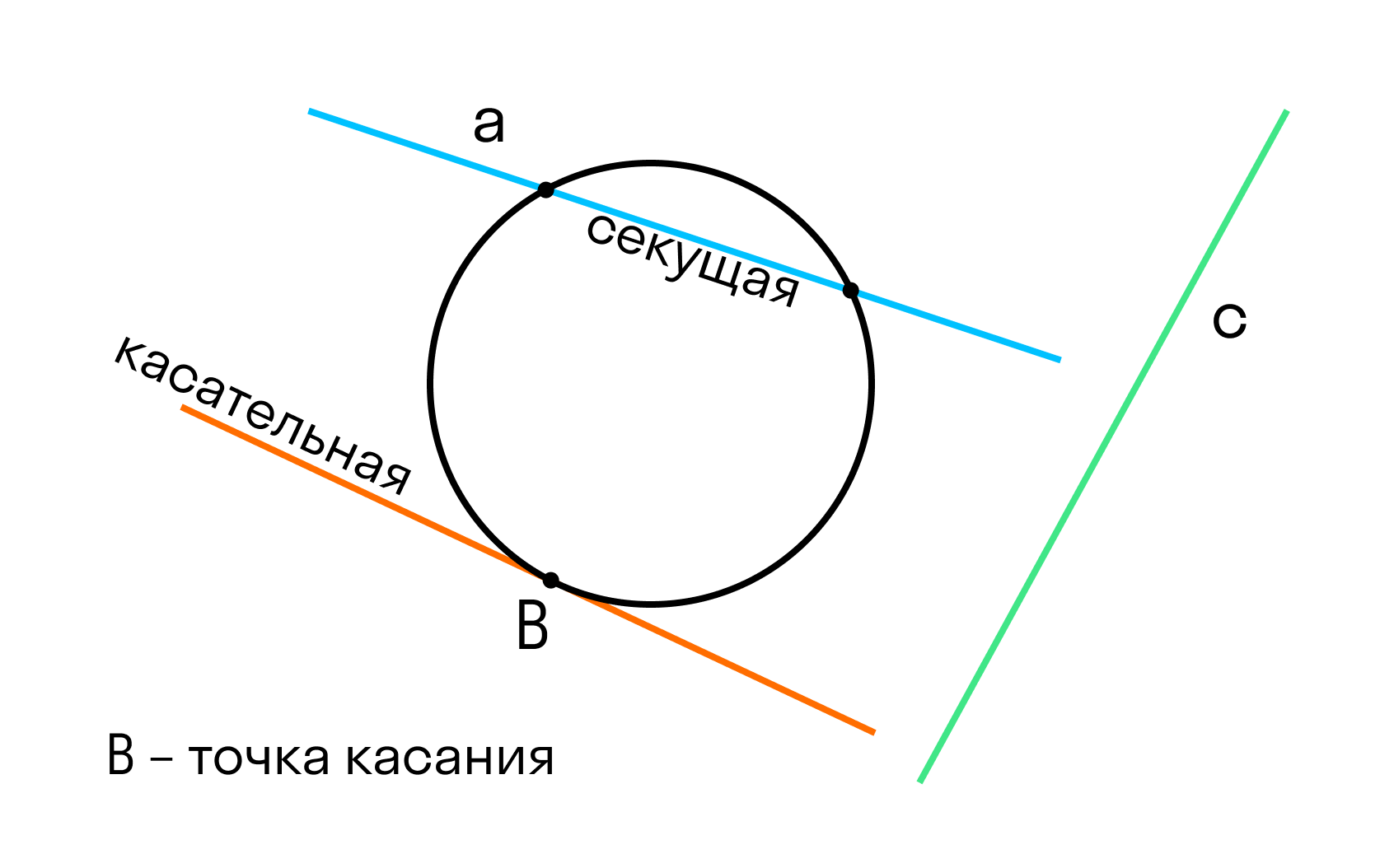
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.

На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

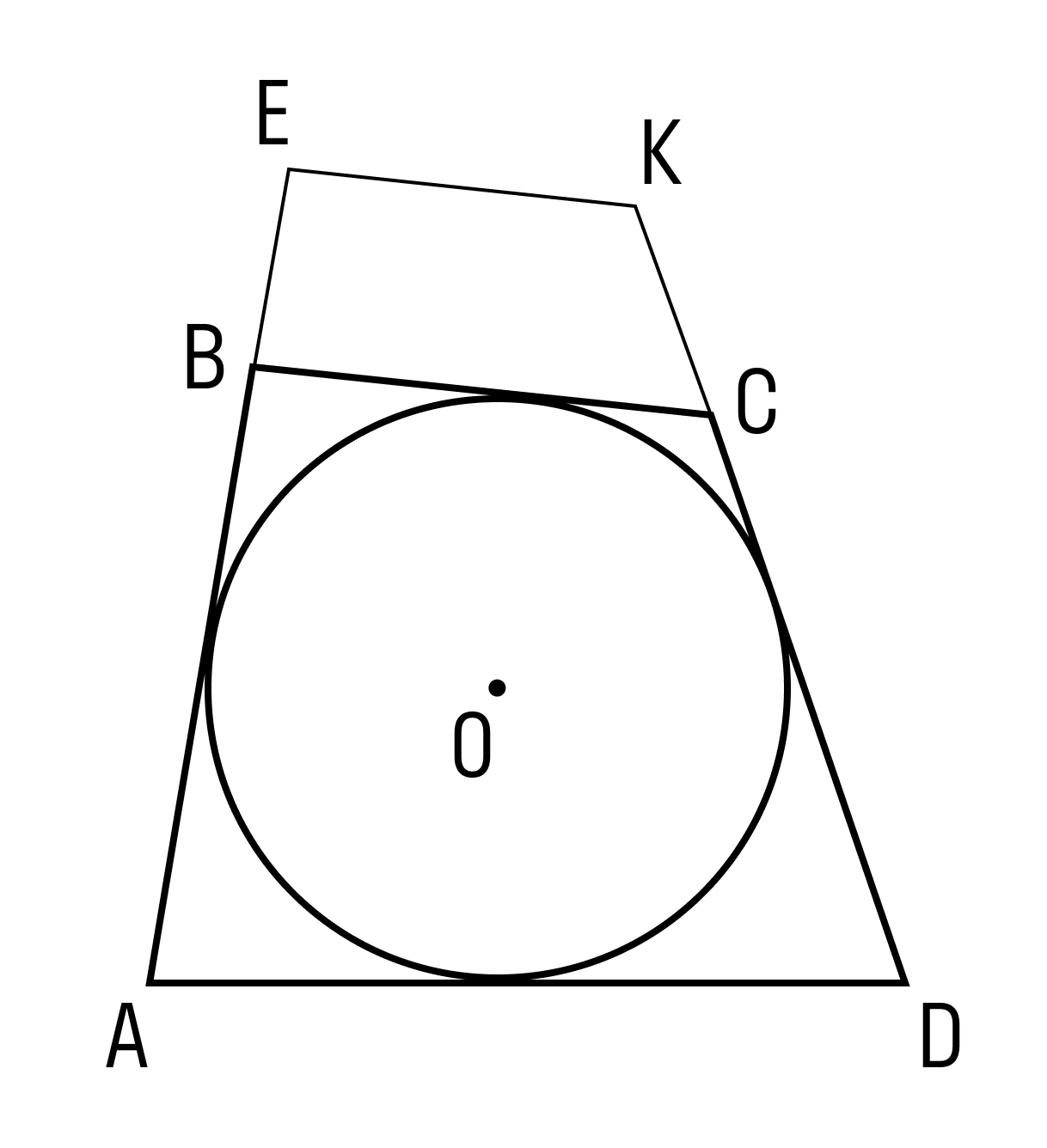
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.

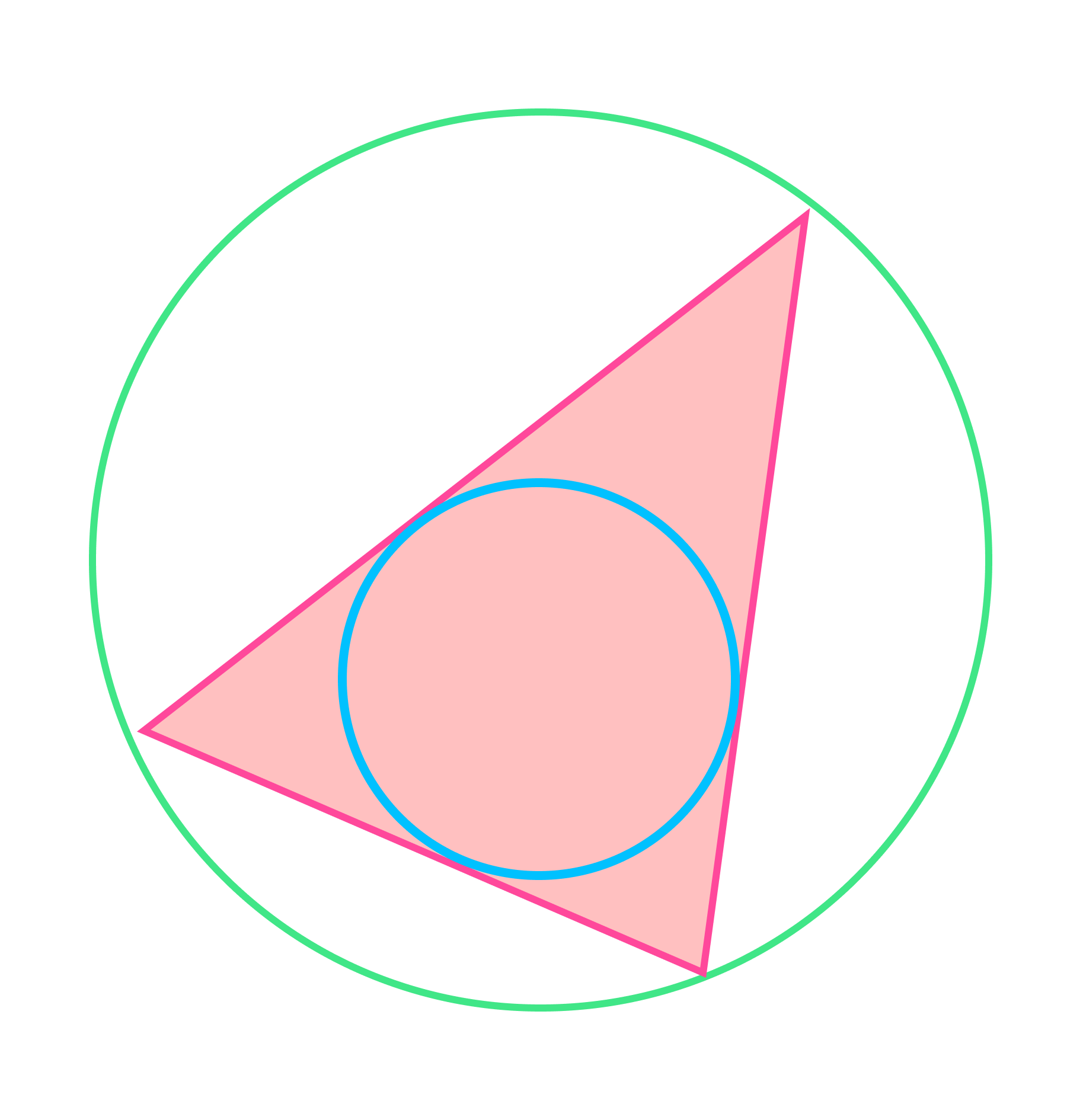
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.

Определение и смысл ЧТД

ЧТД основана на идеи, что поверхность любого материала может быть представлена в виде набора точек или вершин. На основе этих точек строится топографическая карта поверхности, которая позволяет визуально и количественно оценить неровности и дефекты.

Основной смысл ЧТД заключается в том, чтобы получить информацию о состоянии поверхности и выявить дефекты, которые не видны невооруженным глазом

Это особенно важно в случаях, когда поверхность должна быть идеально гладкой или иметь определенные параметры, например, в машиностроении или производстве микрочипов

Использование ЧТД позволяет не только обнаружить дефекты, но и измерить их размеры, форму, глубину и другие характеристики. Это позволяет проанализировать состояние поверхности до, во время и после процесса обработки, а также контролировать качество продукции на всех стадиях производства.

Узнайте, что такое ЧТД и какое значение оно имеет в геометрии

ЧТД является мощным графическим инструментом, который может быть использован для изучения и анализа различных геометрических свойств и теорем связанных с треугольниками. Она позволяет наглядно представить исходные данные и увидеть взаимосвязи между углами и сторонами треугольника.

Важность ЧТД заключается в том, что она помогает студентам и исследователям понять и запомнить геометрические свойства треугольников. Она помогает в изучении различных теорем и правил, связанных с треугольниками, таких как теорема синусов, теорема косинусов, теорема о средних линиях и другие

ЧТД также полезна для решения задач на конкретные геометрические объекты, такие как медианы, биссектрисы и высоты треугольников. Она помогает найти точки пересечения этих линий и легко определить различные углы и отношения сторон.

Зачем нужно знать ЧТД?

Знание ЧТД, или Числа торовых диаграмм, в геометрии существенно помогает в анализе и решении задач, связанных с сетями, цепями, графами и другими объектами схожей структуры. Это полезный инструмент при проектировании и оптимизации систем, соединенных линиями, как в сфере производства, так и в информационных технологиях.

Кроме того, знание ЧТД может значительно упростить работу с графами процессов, транспортных и логистических систем, дорожными картами, геометрическими схемами и даже при проектировании мебели, позволяя быстро ориентироваться в больших объемах информации и находить оптимальные решения.

Зачем нужны аксиомы

Математику изучают в школе не просто так. Большинство забудет все эти уравнения, графики и аксиомы сразу после ЕГЭ в 11 классе.

Задача школьного курса математики состоит в том, чтобы вы освоили научное мышление. Чтобы поняли, как работает наука, как проверяются гипотезы и как доказываются утверждения. И чем отличается частный жизненный опыт от универсальных знаний.

Подробнее о том, чем научное знание отличается от обывательского (и почему это так важно), смотрите в цикле уроков «Как работает наука». Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств

Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих

Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств. Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих.

Простой пример «очевидного» утверждения. Биссектриса треугольника пересекает его противоположную сторону:

Спасибо, Капитан Очевидность. Однако напрямую этот факт ниоткуда не следует. Его можно доказать, например, через тригонометрию или координаты. Но потребовать такое доказательство — отличная задача-гроб на устном экзамене в университет.

Создание системы аксиом — долгий и кропотливый процесс. Классическая евклидова геометрия, которую изучают в школе, основана на аксиомах, которые формировались более двух тысяч лет. Основоположник этих аксиом — Евклид — жил в III веке до н.д. Собственно, потому геометрия и называется евклидовой.

Зато когда система аксиом построена, все последующие теоремы выводятся из неё через логические рассуждения. Без привлечения наглядных иллюстраций и «очевидных соображений». Вот здесь и начинается настоящая наука.:)

Что дает итоговое сочинение

В первую очередь зачет за итоговое сочинение гарантирует, что 11-классник будет допущен к сдаче ЕГЭ. Даже ребята, которые сдают ЕГЭ в 10-м классе, на следующий год пишут сочинение. 

Также итоговое сочинение — это отличная возможность проверить свои знания в экзаменационной атмосфере. Декабрьский экзамен проходит в том же порядке, что и ЕГЭ в мае-июне: в отдельной аудитории, под наблюдением организаторов и в ограниченное время. Вы можете использовать эту возможность, чтобы проверить, как поведет себя организм в стрессовой обстановке. Это поможет морально и физически подготовиться к следующим  экзаменам.

Наконец, вузы также засчитывают результат итогового сочинения как индивидуальное достижение. Отлично справившись с экзаменом, вы не только получите доступ к ЕГЭ, но и сможете заработать до 10 дополнительных баллов при поступлении. У каждого учебного заведения свои критерии оценки работы — например, ВШЭ дает максимальный балл, если текст написан с опорой на минимум два произведения. Количество баллов, которые добавят за сочинение, также варьируется. Так, МГУ может начислить только 2 балла, зато Государственный институт русского языка им. Пушкина — все 10!

Пример итогового сочинения

Мы подготовили для вас реальный пример итогового сочинения, за который ученик получил зачет по максимальному количеству критериев. Для получения зачета достаточно выполнить три из пяти критериев: обязательно «Соответствие теме» и «Аргументация» и еще один.

Используйте этот текст как пример итогового сочинения — 2025 и заряжайтесь мотивацией на получение зачета

Помимо доступа к экзаменам, хорошо написанное итоговое сочинение гарантирует до 10 дополнительных баллов к сумме ЕГЭ. При поступлении в вузы с высокой конкуренцией вроде Бауманки или Вышки несколько баллов могут стать решающими — это еще один повод ответственно подойти к подготовке. Преподаватели MAXIMUM Education на курсе по итоговому сочинению объясняют ученикам, как писать пробные тексты, и дают развернутую обратную связь, которая на реальном экзамене поможет добиться зачета.