Поверхностный интеграл II рода
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
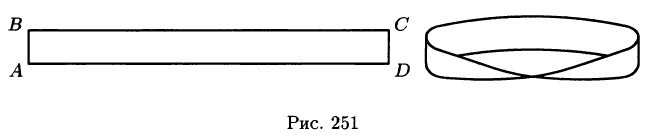
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), — функции, непрерывные в некоторой области D плоскости Оху и т.д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, a В — с D (см. рис. 251).
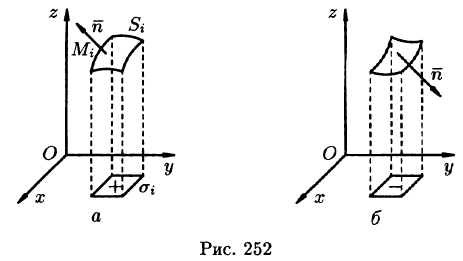
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части , где i = 1,2,…,п, и проектируем их на координатные плоскости. При этом площадь проекции берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е. со знаком «минус», если выбрана нижняя сторона поверхности (или ) (см. рис. 252, б). В этом случае интегральная сумма имеет вид

где — площадь проекции на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.
Предел интегральной суммы (58.1) при если он существует и не зависит от способа разбиения поверхности S на части и от выбора точек называется поверхностным интегралом II рода (по координатам) от функции f(x;y;z) по переменным x и у по выбранной стороне поверхности и обозначается
Итак
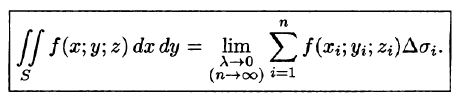
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
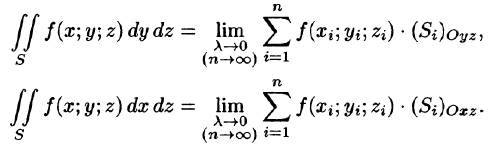
Общим видом поверхностного интеграла II рода служит интеграл
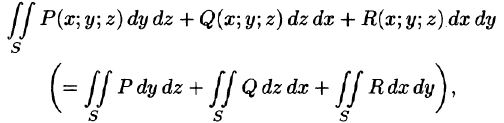
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается , по внутренней .
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности равен сумме интегралов по ее частям (аддитивное свойство), если пересекаются лишь по границе, их разделяющей.
- Если — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
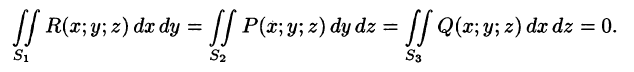
Плоскость, общее уравнение плоскости
Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.
Пусть в пространстве есть три уже известные нам оси координат — Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.
Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:
Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор
перпендикулярен вектору
Вектор
Теперь, используя формулу скалярного произведения векторов
Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости,
Перед решением задач может пригодиться урок о декартовой системе координат. Также хорошо бы владеть материалом о скалярном произведении векторов.
Пример 1. Составить уравнение плоскости, проходящей через точку
Решение. Используем формулу (1), еще раз посмотрим на неё:
В этой формуле числа A , B и C координаты вектора
xyz
Вычисления очень простые: подставляем эти числа в формулу и получаем
Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:
Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида
называется общим уравнением плоскости.
Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.
Как найти эти точки? Чтобы найти точку пересечения с осью Oz , нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0 . Поэтому получаем z = 6 . Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6) .
Точно так же находим точку пересечения плоскости с осью Oy . При x = z = 0 получаем y = −3 , то есть точку B(0; −3; 0) .
И, наконец, находим точку пересечения нашей плоскости с осью Ox . При y = z = 0 получим x = 2 , то есть точку C(2; 0; 0) . По трём полученным в нашем решении точкам A(0; 0; 6) , B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.
Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.
1. При D = 0 уравнение
2. При A = 0 уравнение
Ox
OxOxB =
OyC =
Oz
3. При A = D = 0 уравнение
OxOxA =D =
Oy
Oz
4. При A = B = 0 уравнение
xOyOxAOyB
yOz
xOz
5. При A = B = D = 0 уравнение
z =xOyxOyA = B =D =y =xOzx =yOz
Пример 3. Составить уравнение плоскости P , проходящей через ось Oy и точку
Решение. Итак, плоскость проходит через ось Oy . Поэтому в её уравнении y = 0 и это уравнение имеет вид
AC
P
Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (
Среди них x = 2 , z = 3 . Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:
Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем
Подставив найденное значение A в уравнение
Это и есть уравнение, требуемое в условии примера.
Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение
Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением
Нормальное уравнение плоскости – описание и пример.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz.
Рассмотрим плоскость, которая удалена на расстояние p () единиц от начала координат в положительном направлении нормального вектора плоскости . Будем считать, что длина вектора равна единице. Тогда его координаты равны направляющим косинусам, то есть, , причем . Обозначим расстояние от точки до плоскости как , то есть, точка N лежит на плоскости и длина отрезка ON равна p. Для наглядности отметим все данные на чертеже.
Получим уравнение этой плоскости.
Возьмем точку трехмерного пространства . Тогда ее радиус вектор имеет координаты , то есть, (при необходимости смотрите раздел ). Очевидно, что множество точек определяют описанную ранее плоскость тогда и только тогда, когда на направление вектора равна p, то есть, (смотрите рисунок ниже).
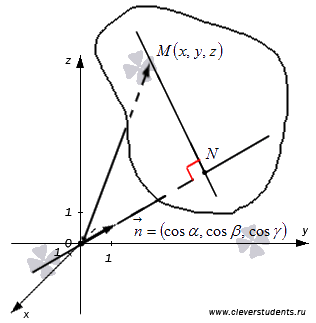
Тогда векторов и дает нам следующее равенство 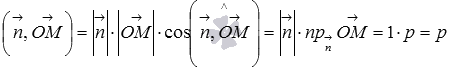 . Это же представляется как
. Это же представляется как ![]() . Сопоставление двух последних равенств дает нам искомое уравнение плоскости . Перенесем p в левую часть, и мы получим уравнение , которое называется нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.
. Сопоставление двух последних равенств дает нам искомое уравнение плоскости . Перенесем p в левую часть, и мы получим уравнение , которое называется нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.
Итак, нормальное уравнение плоскости вида задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .
Следует заметить, что косинусы зачастую явно не фигурирует в нормальном уравнении плоскости, так как и — это некоторые действительные числа, сумма квадратов которых равна единице.
Приведем пример нормального уравнения плоскости.
Пусть плоскость задана в прямоугольной системе координат Oxyz уравнением в нормальном виде . Здесь , нормальный вектор плоскости имеет координаты , его длина равна единице, так как . Более того, заданная плоскость находится на расстоянии 7 единиц от начала координат в направлении вектора , так как p = 7.
Очевидно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости вида , в котором числа A, B и C таковы, что длина нормального вектора плоскости равна единице, а число D неотрицательно.
Осталось разобраться с вопросом: «Как узнать, действительно ли перед нами нормальное уравнение плоскости»? Ответить на него достаточно просто: если выполняются оба условия и , то мы имеем уравнение плоскости в нормальном виде, если же хотя бы одно из условий не выполняется, то уравнение плоскости не является нормальным. Рассмотрим пример.
Пример.
Есть ли среди указанных уравнений уравнения плоскости в нормальном виде?
- ;
- ;
- .
Решение.
Начнем с первого уравнения. Проверим, равна ли длина нормального вектора плоскости единице. Вычислим длину: 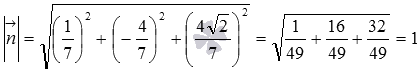 . Осталось убедиться, что число p в этом уравнении положительно. Это действительно так, так как . Таким образом, первое уравнение плоскости является уравнением плоскости в нормальном виде.
. Осталось убедиться, что число p в этом уравнении положительно. Это действительно так, так как . Таким образом, первое уравнение плоскости является уравнением плоскости в нормальном виде.
Второе уравнение плоскости не является нормальным уравнением плоскости, так как не выполняется условие (в этом уравнении ).
В третьем уравнении длина нормального вектора не равна единице: 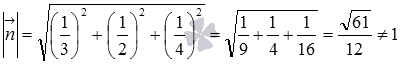 . Поэтому оно не является уравнением плоскости в нормальном виде.
. Поэтому оно не является уравнением плоскости в нормальном виде.
Ответ:
только первое уравнение является нормальным уравнением плоскости.
Теорема о пересекающихся прямых
По сути, это обычные прямые из планиметрии, которые пересекаются в одной точке. Если прямые $a$ и $b$ пересекаются в точке $M$, то обычно это записывается так:
\
Для доказательства рассмотрим две прямые:
Мы видим, что эти прямые пересекаются в точке $M$. Отметим на прямой $a$ произвольную точку $N$, которая не совпадает с $M$:
По Теореме о прямой и точке, доказанной выше, прямая $b$ и точка $N$ однозначно задают плоскость. Обозначим эту плоскость $\alpha $:
Итак, прямая $b\subset \alpha $. Кроме того, точки $M\in \alpha $, $N\in \alpha $. По Аксиоме о прямой и плоскости заключаем, что прямая $a=MN\subset \alpha $.
Итак, обе прямые лежат в плоскости $\alpha $. Единственность такой плоскости следует из того, что любая плоскость, содержащая пересекающиеся прямые $a$ и $b$, содержит, в частности, прямую $b$ и точку $N$. И по предыдущей теореме через эту прямую и точку проходит лишь одна плоскость.
Что называют общим уравнением плоскости
Поговорим об уравнении плоскости для трехмерного пространства.
Плоскость в трехмерном пространстве
Разбираясь в чертежах, необходимо знать стандартные обозначения.
Все геометрические плоскости обычно прописывают прописными буквами греческого алфавита, а прямые обозначают большими буквами. Иногда для обозначения используют греческий алфавит, но с подстрочными индексами снизу. Чтобы изобразить ее, необходимо нарисовать параллелограмм, который создаст впечатление плоскости в пространстве.
Поскольку плоскость является бесконечной структурой, мы сможем отобразить лишь ее небольшой кусок. Поэтому вокруг параллелограмма изображают неровный овал, произвольной формы.
В реальности она могут быть расположены в любом произвольном порядке, иметь любой наклон или угол.
Если имеется прямоугольная система координат, расположенная в трехмерном пространстве, то в уравнении будут 3 неизвестных. Чтобы добиться равенства, нужно поставить в уравнение координаты точки, которая расположена именно в данной плоскости.
Если будут поставлены координаты другой точки, не из данной плоскости, тождество не получится.
Представим, что в 3-х мерном изображении и прям-ной координатной системы Oxyz общее уравнение, проходящей через две линии, имеет 3 неизвестных: x, yes и z. Они удовлетворяют координатам плоскости.
Значит, что при использовании этих данных для каждой из точек, лежащей на плоскости, обязательно должно получиться равенство. Если равенства нет, то точка к ней не относится.
Для записи общего уравнения через точку, необходимо вспомнить определение прямой линии, перпендикулярной заданной плоскости.
Правило:
Каждая прямая будет перпендикулярной к плоскости, если она перпендикулярна относительно прямой, принадлежащей данной плоскости.
Это значит, что каждый нормальный вектор, соответствующий исходной плоскости, будет перпендикуляром к нулевому вектору, принадлежащему плоскости. Это является доказательством теоремы, которая будет определять вид общего уравнения плоскости.
Это значит, что каждый нормальный вектор, соответствующий исходной плоскости, будет перпендикуляром к нулевому вектору, принадлежащему плоскости. Это является доказательством теоремы, которая будет определять вид общего уравнения.
Разновидности систем координат
Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.
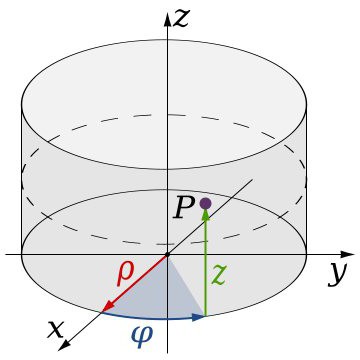
Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.
Строительные задания в пространстве
Все планиметрические конструкции выполнены с помощью чертежных инструментов с использованием единой плоскости. Обычные инструменты рисования больше не подходят, так как вы не можете рисовать символы в пространстве.
Кроме того, при объемном строительстве в пространстве, появляется необходимость в построении еще одного нового элемента — новой плоскости. Ее невозможно построить в пространстве такими простыми средствами.
Поэтому при строительстве в пространстве, строителям необходимо точно знать, как лучше построить ту или иную конструкцию.
Во всех конструкциях в пространстве мы можем предполагать следующие качества:
- Плоскость можно выстроить, если найдены элементы, точно определяющие ее положение в исходном пространстве. Мы можем построить плоскость, если она будет проходить через 3 заданные точки, через прямую линию и наружную точку. А также иметь 2 пересекающиеся или две параллельные прямые.
- При условии, что даны 2 пересекающиеся плоскости, то обязательно будет существовать и линия их пересечения, которую можно легко найти.
- Если дана плоскость в пространстве, то можно легко сделать любые планиметрические конструкции.
Создание любой конструкции в пространстве означает сокращение ее до конечного числа указанных базовых структур. Эти базовые знания можно использовать для решения более сложных задач.
Именно так решаются задачи построения стереометрии.
Пример задания на построение в пространстве
Задача.
Нужно обнаружить точку, где будут пересекаться заданная прямая А с плоскостью Р. Затем необходимо составить нужное уравнение для прямой, проходящей через заданные точки: А (1; 2) и B (-1; 1).
Решение:
- подставляем в уравнение (8) х 1 = 1, y 1 = 2, х 2 = -1; y 2 = 1;
- получаем либо 2y-4 = х-1, либо х-2y + 3 = 0.
Использование плоскости xoy в математических расчетах
Использование плоскости xoy позволяет решать задачи, связанные с геометрией, алгеброй и анализом. Например, с ее помощью можно находить точки пересечения прямых и кривых, определять расстояние между точками, находить производные и интегралы функций, а также строить графики функций.
Для работы с плоскостью xoy используются математические методы и инструменты, такие как системы координат, уравнения прямых и кривых, геометрические фигуры и интегральное исчисление.
Примером использования плоскости xoy может служить решение задачи о нахождении пересечения двух прямых. Сначала задается уравнение каждой прямой в виде y = k1x + b1 и y = k2x + b2, где k1 и k2 — коэффициенты наклона прямых, а b1 и b2 — свободные члены. Затем уравнения прямых решаются системой уравнений, где x и y — неизвестные, и находятся их значения, образующие точку пересечения на плоскости xoy.
Нормальное уравнение плоскости
В данной статье мы рассмотрим нормальное уравнение плоскости. Приведем примеры построения нормального уравнения плоскости по углу наклона нормального вектора плоскости от осей Ox, Oy, Oz и по расстоянию r от начала координат до плоскости. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
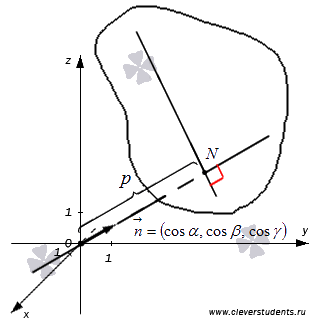
Пусть в пространстве задана декартова прямоугольная система координат. Тогда нормальное уравнение плоскости Ω представляется следующей формулой:
| xcosα+ycosβ+zcosγ−r=0, | (1) |
где r− расстояние от начала координат до плоскости Ω, а α,β,γ− это углы между единичным вектором n, ортогональным плоскости Ω и координатными осьями Ox, Oy, Oz, соответственно (Рис.1). (Если r>0, то вектор n направлен в сторону плоскости Ω, если же плоскость проходит через начало координат, то направление вектора n выбирается произвольной).
Выведем формулу (1). Пусть в пространстве задана декартова прямоугольная система координат и плоскость Ω (Рис.1). Проведем через начало координат прямую Q, перпендикулярную плоскости Ω, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором
ORn
Выразим уравнение плоскости Ω через следующие параметры: длину отрезка
α, β, γnOx, Oy, Oz
Так как вектор n является единичным вектором, то его проекции на Ox, Oy, Oz будут иметь следующие координаты:
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M (x,y, z). Точка M лежит на плоскости Ω тогда и только тогда, когда проекция вектора
Rr
| (3) |
Скалярное произведение векторов n и
| , | (4) |
где
nαn
Поскольку n единичный вектор, то (4) можно записать так:
| . | (5) |
Учитывая, что n=<cosα, cosβ, cosγ>,
| . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosα+ycosβ+zcosγ−r=0. | (7) |
Мы получили нормальное уравнение плоскости Ω. Уравнение (7) (или (1)) называется также нормированным уравнением плоскости . Вектор n называется нормальным вектором плоскости .
Как было отмечено выше, число r в уравнении (1) показывает расстояние плоскости от начала координат. Поэтому, имея нормальное уравнение плоскости легко определить расстояние плоскости от начала координат. Для проверки, является ли данное уравнение плоскости уравнением в нормальном виде, нужно проверить длину нормального вектора этой плоскости и знак числа r, т.е. если |n|=1 и r>0, то данное уравнение является нормальным (нормированным) уравнением плоскости.
Пример 1. Задано следующее уравнение плоскости:
| . | (7) |
Определить, является ли уравнение (7) нормальным уравнением плоскости и если да, то определить расстояние данной плоскости от начала координат.
Решение. Нормальный вектор плоскости имеет следующий вид:
Определим длину вектора n:
Ответ: Длина вектора n равна 1,
Каноническое уравнение прямой
Пусть декартова система координат будет установлена на плоскости Оху.
Задача: получить простое уравнение и если она является точкой прямой и и вектор кода прямой И.
- Возьмем любую точку А на плоскости Р.
- Через данную точку А и исходную прямую а проведем простую плоскость Q. Она будет пересекать плоскость Р вдоль новой прямой b.
- В плоскости Q находим точку С — пересечение прямых линии а и b.
- Эта точка будет желательной. Если прямые а и b окажутся параллельными, то у проблемы не будет решения.
Рассмотрим уравнение прямой, которая является линией пересечения двух плоскостей:
- Бесчисленные плоскости проходят через каждую прямую в пространстве.
- Любые два из них, пересекающиеся, определяют его в пространстве.
- Это значит, что уравнения для 2 плоскостей, вместе взятые, представят собой уравнение для прямой.
Вывод:
Любые 2 непар-ные плоскости, когда они заданы единым уравнением, можно определить по линии их взаимного пересечения. Эти уравнения именуют общими простыми уравнениями.
Рассмотрим уравнение прямой линии, проходящей через две точки:
- Заданы точки А (1х; 1у) и B (2х; 2у).
- Уравнение для прямой, проходящей через точки А (1х; 1у) и B (2х; 2у), когда они лежат на прямой, параллельной оси О х (y 2 -y 1 = 0) или оси О y (2х -1х = 0), то уравнение будет иметь вид: y = 1у или х = 1х.
Пусть будет плавающая точка, принадлежащая прямой А. Тогда получаем направляющий вектор для прямой А, он будет иметь идентичные координаты. Набор всех точек на данной плоскости определит прямую, проходящую через точку и имеющую вектор направления, при условии, что векторы коллинеарны.
Каноническое уравнение для прямой, лежащей на плоскости, можно задать в прям-ной системе к-т Оху, как прямую, проходящую через точку и имеющую свой вектор направления.
Пример канонического уравнения
Если уравнение является каноническим для прямой, то она должна соответствовать этому уравнению и будет проходит через точку, которая является ее вектором направления.
Нужно обратить внимание на следующие важные факты:
- Если направляющий вектор — это прямая линия, которая проходит через точку, то ее каноническое ур-ние можно составить.
- Когда один вектор является направляющим для прямой, то каждый из векторов также будет направляющим для заданной прямой.
- Поэтому каждое уравнение для любой другой прямой в канонической форме будет соответствовать заданной прямой.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
Разобьем поверхность S на части Обозначим через проекцию на плоскость Оху. При этом область D окажется разбитой на п частей Возьмем в произвольную точку и восстановим перпендикуляр к плоскости Оху до пересечения с поверхностью S . Получим точку на поверхности . Проведем в точке М, касательную плоскость и рассмотрим ту ее часть , которая на плоскость Оху проектируется в область (см. рис. 247). Площади элементарных частей обозначим как соответственно. Будем приближенно считать, что
![]()
Обозначив через, острый угол между осью Oz и нормалью п, к поверхности в точке получаем:
![]()
(область есть проекция на плоскость Оху).
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке есть
![]()
где — координаты нормального вектора к плоскости. Острый угол уг есть угол между векторами и
![]()
Следовательно,
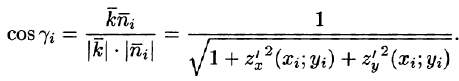
Равенство (57.4) принимает вид
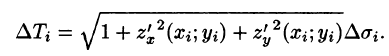
В правой части формулы (57.2) заменим (учитывая (57.3)) на полученное выражение для , a заменим на Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра (а следовательно, и ), получаем формулу
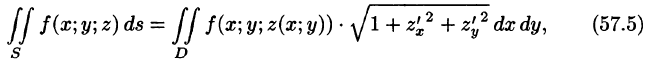
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
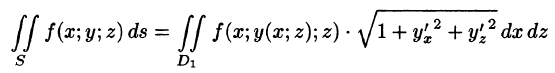
и
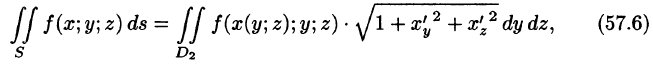
где — проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
Пример:
Вычислить — часть плоскости расположенной в I октанте (см. рис. 248).
Решение:
Запишем уравнение плоскости в виде
Находим По формуле (57.5) имеем:
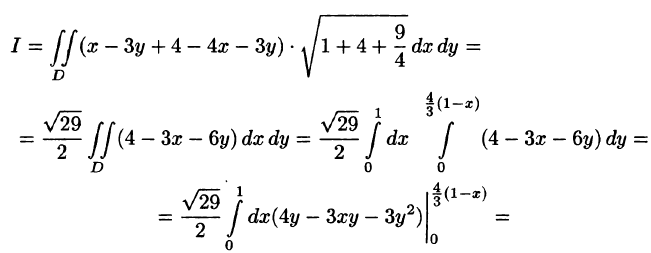
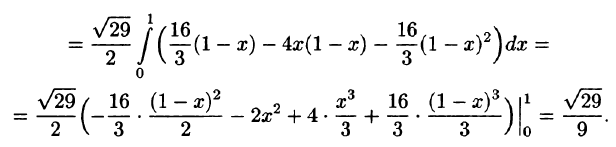
Пример:
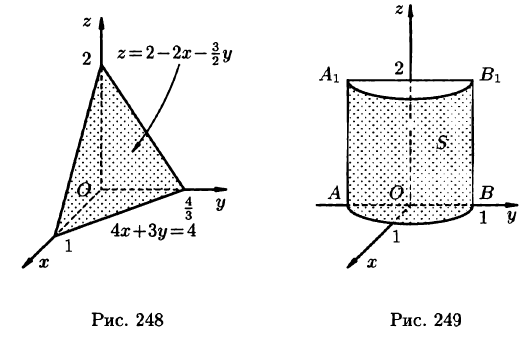
Вычислить
где S — часть цилиндрической поверхности отсеченной плоскостями z = 0, z = 2 (см. рис. 249).
Решение:
Воспользуемся формулой (57.6). Поскольку
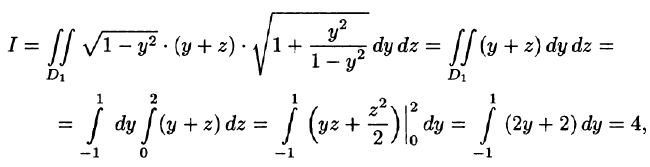
то где — прямоугольник
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
или
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть Для нахождения массы поверхности:
- Разбиваем поверхность S на п частей площадь которой обозначим .
- Берем произвольную точку в каждой области . Предполагаем, что в пределах области плотность постоянна и равна значению ее в точке .
- Масса области мало отличается от массы фиктивной однородной области с постоянной плотностью
4. Суммируя по всей области, получаем:
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей , т. е.
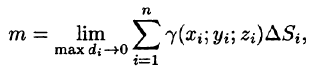
т. е.
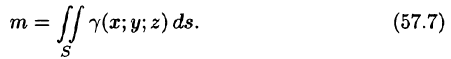
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
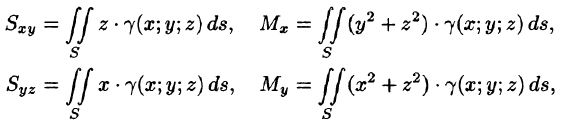
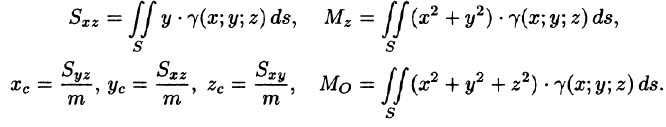
Пример:
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение ![]() — поверхностная плотность полусферы.
— поверхностная плотность полусферы.
По формуле (57.7) находим:
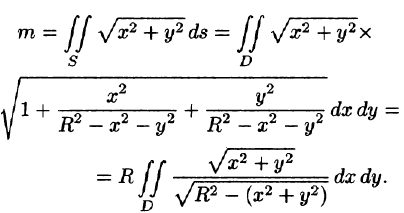
Переходим к полярным координатам:
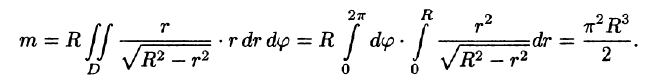
внутренний интеграл вычислен с помощью подстановки r= Rsint:
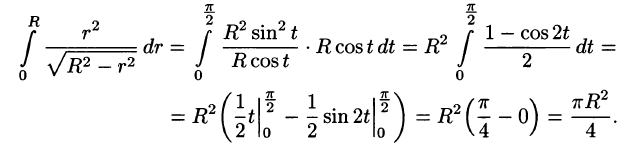
Примеры построения сечений
Рассмотрим несколько примеров построения сечений в различных фигурах.
Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р.
Решение. Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить.
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить.
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т.
4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М.
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить.
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ.
Пример 2. Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1).
Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е.
Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А1В1 в точке О.
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС1) и точки О и М в плоскости (АВВ1).
Тогда КТОМЕ — сечение призмы.
Пример 3. Дан куб ABCDA1B1C1D1. М — середина ребра АА1. Постройте сечение куба, которое будет параллельно диагонали куба А1С и будет проходить через точки М и В.
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА1С). Проведем в ней прямую, параллельную А1С из точки М. Пусть она пересечет АС в точке К.
2. Тогда МК — средняя линия треугольник АА1С, значит К — середина АС.
Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники».
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) — их можно соединить.
4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам.
Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм».
Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD.
Следовательно, прямую ВК можно продлить до точки D.
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD1) и точки М и В в плоскости (ABB1).
Тогда сечением будет треугольник DMB.
Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры.
Уравнение плоскости, проходящей через три точки
Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки
и вектора нормали, являются также три точки, не лежащие на одной прямой.
Пусть даны три различные точки ,
и ,
не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы и
не коллинеарны, а поэтому
любая точка плоскости
лежит в одной плоскости с точками , и
тогда и только тогда, когда векторы
, и
компланарны, т.е. тогда и только тогда,
когда смешанное произведение этих векторов равно нулю.
Используя выражение смешанного произведения в координатах, получим уравнение плоскости
(3)
После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.
Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:
, ,
и определить частный случай общего уравнения прямой, если такой имеет место.
Решение. По формуле (3) имеем:
Раскрываем определитель по первой строке:
Получили общее уравнение плоскости
или после деления на -2:
.
Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.
Решения типичных задач, которые бывают на контрольных работах —
в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
Использование плоскости xoy в архитектуре
Архитекторы используют плоскость xoy для создания точных и подробных чертежей зданий, а также для планирования помещений и расстановки мебели. На плоскости xoy отображаются все грани, стены и окна здания, а также указываются размеры и пропорции каждого элемента.
Использование плоскости xoy в архитектуре позволяет архитекторам легко видеть и представлять здание в двухмерном пространстве. Это помогает им визуализировать и понять различные аспекты здания, такие как его размеры, форма и композиция.
Кроме того, плоскость xoy используется при проектировании ландшафта. Ландшафтные архитекторы используют плоскость xoy для отображения садов, парков и других элементов ландшафтного дизайна. Они могут точно расположить пути, дорожки, водные объекты и растения на этой плоскости, чтобы создать эстетически привлекательные и функциональные пространства.
Таким образом, использование плоскости xoy в архитектуре играет важную роль в создании точных и детальных планов зданий и ландшафтных ансамблей. Это позволяет архитекторам и ландшафтным архитекторам визуализировать и понять свои проекты, а также представить их заказчикам и другим заинтересованным сторонам.





























