Fundamentals of numerical computation

Определение[править | править код]

Норма вектора

Норма в векторном пространстве V {\displaystyle V\ } над полем вещественных или комплексных чисел — это функционал pV→R+{\displaystyle p\colon V\to \mathbb {R_{+}} }, обладающий следующими свойствами:

1. p(x)=⇒x=V;{\displaystyle p(x)=0\Rightarrow x=0_{V};}
2. ∀x,y∈V,p(x+y)⩽p(x)+p(y){\displaystyle \forall x,y\in V,p(x+y)\leqslant p(x)+p(y)} (неравенство треугольника);
3. ∀α∈C,∀x∈V,p(αx)=|α|p(x).{\displaystyle \forall \alpha \in \mathbb {C} ,\forall x\in V,p(\alpha \,x)=|\alpha |p(x).}

Эти условия являются аксиомами нормы.

Векторное пространство с нормой называется нормированным пространством, а условия (1—3) — также аксиомами нормированного пространства.

Из аксиом нормы очевидным образом вытекает свойство неотрицательности нормы:

∀x∈V,p(x)⩾{\displaystyle \forall x\in V,p(x)\geqslant 0}.

Действительно, из третьего свойства следует: p(V)=p(⋅V)=⋅p(V)={\displaystyle p(0_{V})=p(0\cdot 0_{V})=0\cdot p(0_{V})=0}, а из свойства 2 — ∀x∈V=p(V)=p(x−x)⩽p(x)+p(−x)=2p(x){\displaystyle \forall x\in V\colon 0=p(0_{V})=p(x-x)\leqslant p(x)+p(-x)=2p(x)}.

Чаще всего норму обозначают в виде: ‖⋅‖{\displaystyle \|\cdot \|}. В частности, ‖x‖{\displaystyle \|x\|} — это норма элемента x{\displaystyle x} векторного пространства R{\displaystyle \mathbb {R} }.

Вектор с единичной нормой (‖x‖=1){\displaystyle \left(\|x\|=1\right)} называется единичным или нормированным.

Любой ненулевой вектор x{\displaystyle x} можно нормировать, то есть разделить его на свою норму: вектор x‖x‖{\displaystyle {\frac {x}{\|x\|}}} имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.

Норма матрицы

Нормой матрицы A{\displaystyle A} называется вещественное число ‖A‖{\displaystyle \|A\|}, удовлетворяющее первым трём из следующих условий:

1. ‖A‖⩾{\displaystyle \|A\|\geqslant 0}, причём ‖A‖={\displaystyle \|A\|=0} только при A= {\displaystyle A=0\ };
2. ‖αA‖=|α|⋅‖A‖{\displaystyle \|\alpha A\|=|\alpha |\cdot \|A\|}, где α∈R{\displaystyle \alpha \in \mathbb {R} };
3. ‖A+B‖⩽‖A‖+‖B‖{\displaystyle \|A+B\|\leqslant \|A\|+\|B\|};
4. ‖AB‖⩽‖A‖⋅‖B‖{\displaystyle \|AB\|\leqslant \|A\|\cdot \|B\|}.

Если выполняется также и четвёртое свойство, норма называется субмультипликативной. Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов. Очевидно, что все подчинённые матричные нормы субмультипликативны.

Матричная норма ‖⋅‖ab{\displaystyle \|\cdot \|_{ab}} из Km×n{\displaystyle K^{m\times n}} называется согласованной с векторной нормой ‖⋅‖a{\displaystyle \|\cdot \|_{a}} из Kn{\displaystyle K^{n}} и векторной нормой ‖⋅‖b{\displaystyle \|\cdot \|_{b}} из Km{\displaystyle K^{m}} если справедливо:

‖Ax‖b⩽‖A‖ab‖x‖a{\displaystyle \|Ax\|_{b}\leqslant \|A\|_{ab}\|x\|_{a}}

для всех A∈Km×n,x∈Kn{\displaystyle A\in K^{m\times n},x\in K^{n}}.

Норма оператора

Норма оператора A{\displaystyle A} — число, которое определяется так:

‖A‖=sup‖x‖=1‖Ax‖{\displaystyle \|A\|=\sup _{\|x\|=1}\|Ax\|},

где A{\displaystyle A} — оператор, действующий из нормированного пространства L{\displaystyle L} в нормированное пространство K{\displaystyle K}.

Это определение эквивалентно следующему:

‖A‖=supx≠‖Ax‖‖x‖{\displaystyle \|A\|=\sup _{x\neq 0}{\frac {\|Ax\|}{\|x\|}}}

Свойства операторных норм:

1. ‖A‖⩾{\displaystyle \|A\|\geqslant 0}, причём ‖A‖={\displaystyle \|A\|=0} только при A={\displaystyle A=0};
2. ‖αA‖=|α|⋅‖A‖{\displaystyle \|\alpha A\|=|\alpha |\cdot \|A\|}, где α∈R{\displaystyle \alpha \in \mathbb {R} };
3. ‖A+B‖⩽‖A‖+‖B‖{\displaystyle \|A+B\|\leqslant \|A\|+\|B\|};
4. ‖AB‖⩽‖A‖⋅‖B‖{\displaystyle \|AB\|\leqslant \|A\|\cdot \|B\|}.

В конечномерном случае, оператору в некотором базисе соответствует матрица — матрица оператора. Если норма на пространстве(пространствах), где действует оператор, допускает одно из стандартных выражений в базисе, то свойства нормы оператора повторяют аналогичные свойства нормы матрицы.

Свойства линейных операций[править]

Коммутативность сложения векторовАссоциативность сложения векторов

Сложение векторов коммутативно: a+b=b+a{\displaystyle \mathbf {a} +\mathbf {b} =\mathbf {b} +\mathbf {a} }.

Сложение векторов ассоциативно: (a+b)+c=a+(b+c){\displaystyle (\mathbf {a} +\mathbf {b} )+\mathbf {c} =\mathbf {a} +(\mathbf {b} +\mathbf {c} )}.

Прибавление нулевого вектора к любому не меняет последнего: a+=a{\displaystyle \mathbf {a} +\mathbf {0} =\mathbf {a} }.
Очевидно, OA→+AA→=OA→{\displaystyle {\overrightarrow {OA}}+{\overrightarrow {AA}}={\overrightarrow {OA}}}.

Для любого вектора a=AB→{\displaystyle \mathbf {a} ={\overrightarrow {AB}}} существует вектор −a=BA→{\displaystyle -\mathbf {a} ={\overrightarrow {BA}}} такой, что a+(−a)={\displaystyle \mathbf {a} +(-\mathbf {a} )=\mathbf {0} } или AB→+BA→=AA→={\displaystyle {\overrightarrow {AB}}+{\overrightarrow {BA}}={\overrightarrow {AA}}=\mathbf {0} }.

Умножение вектора на число ассоциативно: (αβ)a=α(βa){\displaystyle (\alpha \beta )\mathbf {a} =\alpha (\beta \mathbf {a} )}.
Умножение вектора на число дистрибутивно относительно сложения чисел: (α+β)a=αa+βa{\displaystyle (\alpha +\beta )\mathbf {a} =\alpha \mathbf {a} +\beta \mathbf {a} }.

Доказательство сводится к перечислению всех возможных знаков α{\displaystyle \alpha } и β{\displaystyle \beta }, в каждом случае утверждение очевидно.

Дистрибутивность умножения векторов относительно сложения

Умножение вектора на число дистрибутивно относительно сложения векторов: α(a+b)=αa+αb{\displaystyle \alpha (\mathbf {a} +\mathbf {b} )=\alpha \mathbf {a} +\alpha \mathbf {b} }.
Это следует из подобия треугольников △OAB{\displaystyle \triangle OAB} и △OA′B′{\displaystyle \triangle OA’B’} на рисунке.

Очевидно, умножение на единицу не меняет вектор: 1a=a{\displaystyle 1\mathbf {a} =\mathbf {a} }.

Примечаниеправить

В алгебре изучаются так называемые алгебраические структуры. Это множества математических объектов, для которых определены некоторые операции, удовлетворяющие некоторым системам аксиом.

Пример такой структуры, изучаемой в линейной алгебре, — так называемое векторное (линейное) пространство. Это множество векторов, для которых определены операции сложения и умножения на элементы некоторого поля (например, поля вещественных чисел), причем эти операции удовлетворяют указанным выше свойствам.

В линейной алгебре изучаются общие свойства таких множеств, их элементы (их называют абстрактными векторами) не обязаны быть геометрическими векторами (хотя чаще всего именно их приводят в качестве наглядного примера).

В аналитической геометрии векторы нужны, в первую очередь для введения системы координат (см. ниже). Благодаря этому удается описать геометрические фигуры при помощи аналитических формул.

Особенности длины вектора

Особенности длины вектора включают:

1. Положительность: длина вектора всегда является положительным числом или нулем. Даже если вектор направлен в обратную сторону, его длина будет положительной.
2. Зависимость от координат: длина вектора зависит от координат его начальной и конечной точки. Изменение какой-либо из этих координат приведет к изменению длины вектора.
3. Выражение через компоненты: длину вектора можно выразить через компоненты вектора с использованием теоремы Пифагора в трехмерном пространстве или теоремы Пифагора для произвольных размерностей.
4. Соотношение скалярного произведения: длина вектора может быть выражена через скалярное произведение самого вектора на себя.

Определение и измерение длины вектора являются важными векторными операциями и широко используются в геометрии, физике и других науках. Знание особенностей длины вектора позволяет более полно понять его свойства и использовать векторные операции для решения различных задач.

Модуль или абсолютная величина вектора

Модуль или абсолютная величина вектора представляет собой его длину, которая определяется по формуле:

Где a_x, a_y, a_z представляют собой координаты вектора в соответствующих осях. Модуль вектора всегда является положительным числом или нулем, но никогда не может быть отрицательным.

Модуль вектора имеет важное значение при решении задач по физике и математике. Он позволяет определить длину перемещения, скорость и ускорение, а также установить равенство или неравенство между векторами

Благодаря модулю вектора можно производить его нормирование, то есть приводить вектор к единичной длине.

Модуль вектора также позволяет определить перпендикулярность двух векторов. Если модуль вектора равен нулю, значит он является нулевым вектором, который не имеет направления и считается коллинеарным любому другому вектору.

Неотрицательность длины вектора

Длина вектора определяется как квадратный корень из суммы квадратов его составляющих. Таким образом, все компоненты вектора возводятся в квадрат, суммируются, и затем из полученной суммы берется квадратный корень.

Такое определение длины вектора обладает следующими особенностями:

• Квадратная корень всегда дает неотрицательное значение, даже если вектор имеет отрицательные компоненты.
• Если вектор состоит из нулевых компонент, его длина будет равна нулю.
• Длина вектора может быть равной нулю только в случае, когда сам вектор также равен нулевому вектору.

Таким образом, неотрицательность длины вектора является важным свойством, которое следует учитывать при работе с векторами и их длинами.

Геометрическая интерпретация длины вектора

Геометрически, длина вектора представляет собой расстояние от начала координат до конца вектора в пространстве. Она может быть вычислена с помощью формулы, которая основана на теореме Пифагора. Для двумерного пространства формула имеет вид:

|AB| = √((x2 — x1)^2 + (y2 — y1)^2)

где (x1, y1) и (x2, y2) — координаты начала и конца вектора, соответственно.

Геометрическая интерпретация длины вектора позволяет наглядно представить, насколько «длинным» или «коротким» является вектор. Она также позволяет определить направление вектора, так как длина вектора всегда положительна.

Длина вектора имеет важное значение во многих областях, включая математику, физику и компьютерную графику. Например, вектоная алгебра и геометрия используют длину вектора для определения углов между векторами и вычисления скалярных произведений

Таким образом, понимание геометрической интерпретации длины вектора является важным аспектом, позволяющим более глубоко и точно изучить свойства и особенности векторов.

Example: the norm of a complex array

Another important example is the norm of a

column vector having complex entries.

Let

be the space of all

complex vectors
(on the complex field
).

In the lecture on inner products,
the inner product between two

vectors

was defined to
bewhere

is the conjugate transpose
of
,

are the

entries of

and

are the complex conjugates of the

entries of
.

The norm induced by this inner product
iswhere
we have used the fact that the modulus

is equal to the square root of

times its complex conjugate
.

Thus, the formula for the norm of a complex vector is not very different from
the formula for real vectors: we just need to replace the absolute values of
the entries of the vector with their moduli.

Example
DefineThen

Применение нормальных векторов в компьютерной графике

Нормальные векторы имеют широкое применение в компьютерной графике и визуализации. Они позволяют определить ориентацию поверхности и взаимодействие света с объектами, что позволяет создавать реалистичные изображения.

Вот некоторые из основных способов применения нормальных векторов в компьютерной графике:

Определение освещения и теней
Нормальные векторы используются для определения направления света и расчета освещенности поверхности. Если нормаль вектор повернут в сторону источника света, то поверхность будет освещена с большей интенсивностью. Это позволяет создать эффекты теней и объемности объектов.

Затенение и расчет отраженного света
Нормальные векторы также используются для расчета затенения объектов и отраженного света. Затенение позволяет создать эффекты плавного перехода цвета на поверхности объекта, а отраженный свет добавляет блеск и отражения визуально.

Определение вектора нормали
В компьютерной графике нормальные векторы используются для определения вектора нормали к поверхности в каждой ее точке

Это позволяет определить ориентацию поверхности и ее наклон, что важно при отображении реалистичных объектов.

Расчет отражения и преломления света
При визуализации преломления света или отражения его от поверхности нормальные векторы играют важную роль. Они позволяют определить угол падения и отражения света от поверхности, что создает эффекты преломления или отражения, такие как отражение лучей на водной поверхности или преломление света через стекло.

В заключение, применение нормальных векторов в компьютерной графике является ключевым элементом для создания реалистичных изображений и эффектов. Они позволяют определить ориентацию поверхности, взаимодействие света с объектами и создать эффекты теней, отражения и преломления света.

Нормализация в векторном пространстве

В векторном пространстве с внутренним произведением и , как правило , процедура, которая для заданного вектора приводит к тому, что он имеет унитарную
норму , называется нормализацией.

Обычная ситуация, в которой используется эта процедура, — построение ортонормированного базиса (или ортонормированной системы, сына) векторного пространства. Предположим, что мы находимся в векторном пространстве размерности , и мы уже знаем полный базис векторов, ортогональных друг другу; то есть мы находимся в случае, когда вектора компонентов множества

составляют .

Чтобы получить ортонормированный базис, просто возьмите каждый из этих векторов по отдельности и разделите каждый на значение его нормы (обратите внимание, что это деление на скаляр, потому что норма вектора является скаляром).

каждый из полученных таким образом векторов будет иметь унитарную норму (поэтому он также будет единицей вектора ). Кроме того, эти векторы будут ортогональны друг другу. Поэтому весь

составляет ортонормированный базис нормированного векторного пространства.

Свойства нормы[править | править код]

1. ‖x‖−‖y‖ ⩽‖x±y‖⩽‖x‖+‖y‖{\displaystyle \|x\|-\|y\|\ \leqslant \|x\pm y\|\leqslant \|x\|+\|y\|}
2. (‖x‖−‖y‖)2⩽‖x±y‖2⩽(‖x‖+‖y‖)2{\displaystyle {{\bigl (}\|x\|-\|y\|{\bigr )}}^{2}\leqslant {\|x\pm y\|}^{2}\leqslant {{\bigr (}\|x\|+\|y\|{\bigl )}}^{2}}
3. ‖x‖2+‖y‖2−‖x−y‖22‖x‖‖y‖∈−1,1{\displaystyle {\frac {\|x\|^{2}+\|y\|^{2}-\|x-y\|^{2}}{2\|x\|\|y\|}}\in }
4. ‖V‖=‖x−x‖=‖x‖=⋅‖x‖={\displaystyle \|0_{V}\|=\|x-x\|=\|0x\|=0\cdot \|x\|=0}
5. =‖x−x‖⩽‖x‖+‖−x‖=2‖x‖⇒‖x‖⩾{\displaystyle 0=\|x-x\|\leqslant \|x\|+\|-x\|=2\|x\|\Rightarrow \|x\|\geqslant 0}

Эквивалентность норм

Две нормы p{\displaystyle p} и q{\displaystyle q} на пространстве V{\displaystyle V} называются эквивалентными, если существует две положительные константы C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}} такие, что для любого x∈V{\displaystyle x\in V} выполняется C1p(x)⩽q(x)⩽C2p(x){\displaystyle C_{1}p(x)\leqslant q(x)\leqslant C_{2}p(x)}. Эквивалентные нормы задают на пространстве одинаковую топологию. В конечномерном пространстве все нормы эквивалентны.

L1 Norm

The L1 norm also known as the taxi-cab norm or the Manhattan norm. Is another common way to normalize vectors. The formula is given below:

\(||\vec{v}||_1 =\Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^1\Big)^{\frac{1}{1}}\)

It may be slightly perplexing why the \(\frac{1}{1}\) exponent has been included in the formula above. However, it will soon become clear. Note that we could just as easily have written the formula above as:

\(||\vec{v}||_1 = \sum\limits_{i=1}^{n}|\vec{v}_i| \)

Python function for L1 norm

Example

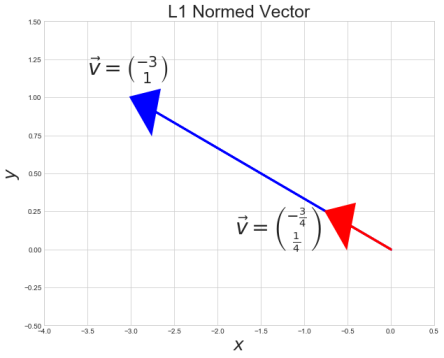
Take the following vector \(\vec{v}\)

\(\vec{v} = \begin{bmatrix} -3 \\ 1 \\ \end{bmatrix} \hspace{0.5cm} \)

Take the L1 norm

\(||\vec{v}||_1 = (|x|^1 + |y|^1)^\frac{1}{1} = |x| + |y|\)

\(4 = |-3| + |1|\)

Normalize the vector by the L1 norm

\(\hat{v} = \begin{bmatrix} \frac{3}{( |-3|+|1|)} \\ \frac{3}{( |-3|+|1|)} \\ \end{bmatrix} = \begin{bmatrix} \frac{-3}{4} \\ \frac{1}{4} \\ \end{bmatrix} \)

Check the L1 norm of the resulting vector equals 1

\(|x| + |y| =1\)

\(|-\frac{3}{4}| + |\frac{1}{4}| = \frac{4}{4} = 1\)

What does that look like?

Let’s normalize the random vectors we created at the beginning of the document using the L1 norm and inspect the resulting shape. 

As with the L2 norm we see an nice shape emerge after normalizing the vectors. Whereas the L2 norm vectors produced a circle, the L1 shows a diamond. 

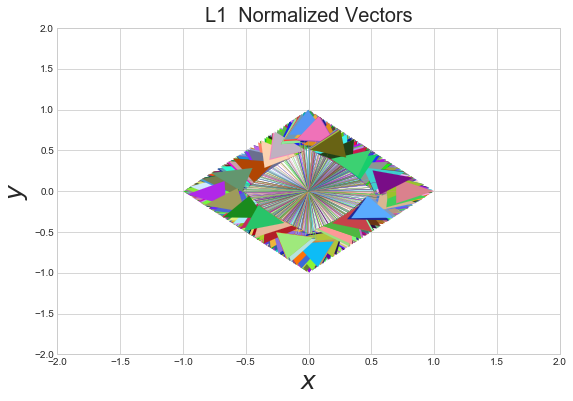
What can we say about the L1 norm?

1) The L1 norm will always be greater than or equal to the L2 norm. Why? Think back to the fact that the L1 norm is also known as the taxicab norm, we could think of the L2 norm as the as the crow flies distance, whereas the L1 norm is equivalent to taking a taxi along streets that requires turns.

2)  When we normalize a 2d vector by the L1 norm. The resulting vector’s elements \(|x| + |y| = 1\) 

3) When thinking of the L1 norm in 2d we should think of a diamond 

In this section we will compare the formulae for the L1 and L2 norm. Recall the formula for the L1 norm for which a seemingly unnecessary exponents were included. Observe the formulae for the L1 and L2 norm below:

\(||\vec{v}||_1 = \Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^1\Big)^{\frac{1}{1}} \\ ||\vec{v}||_2 = \Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^2\Big)^{\frac{1}{2}} \\ \)

You may notice a pattern. Although Let’s add one more to show the pattern:

\(||\vec{v}||_3 = \Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^3\Big)^{\frac{1}{3}} \\ \)

Definition of norm

We are going to give an abstract, axiomatic definition of norm. Later we will
show some examples of norm to clarify its meaning.

Definition
Let

be a vector space. A norm on

is a function

that associates to each

a positive real number, denoted by
,
which has the following properties.

1. Definiteness:

2. Absolute
   homogeneity:where

   is the field over which the vector space is defined (i.e., the set of scalars
   used for scalar multiplication);

   denotes the absolute value if

   and the modulus if
   .

3. Triangle
   inequality:

These properties are pretty intuitive.

As the norm is a measure of the length of a vector, it is reasonable to
require that it should always be a positive number.

The definiteness property imposes that all vectors except the zero vector
should have a strictly positive length.

Absolute homogeneity means that if you scale up (or down) a vector by a factor
,
then its length is re-scaled accordingly.

Finally, in the triangle inequality,

is to be interpreted as the side of a triangle, while

and

are the other two sides. A well-known fact from geometry is that the length of
one side of a triangle is less than the sum of the lengths of the other two
sides. The triangle inequality axiom extends this property to the notion of
length in an abstract vector space.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям этой прямой.

Если рассматривать прямую в прямоугольной системе координат Oxy, то ей будут соответствовать уравнение прямой на плоскости некоторого вида, а нормальные векторы прямой будут определяться своими координатами (смотрите статью координаты вектора). При этом встает вопрос: «как найти координаты нормального вектора прямой, когда нам известно уравнение этой прямой»?

Найдем ответ на поставленный вопрос для прямых, заданных на плоскости уравнениями различного вида.

Если прямую линию на плоскости определяет общее уравнение прямой вида , то коэффициенты А и B представляют собой соответствующие координаты нормального вектора этой прямой.

Пример.

Найдите координаты какого-нибудь нормального вектора прямой .

Решение.

Так как прямая задана общим уравнением, то мы сразу можем записать координаты ее нормального вектора – ими являются соответствующие коэффициенты перед переменными x и y. То есть, нормальный вектор прямой имеет координаты .

Ответ:

Одно из чисел A или B в общем уравнении прямой может равняться нулю. Это не должно Вас смущать. Рассмотрим на примере.

Пример.

Укажите любой нормальный вектор прямой .

Решение.

Нам дано неполное общее уравнение прямой. Его можно переписать в виде , откуда сразу видны координаты нормального вектора этой прямой: .

Ответ:

Уравнение прямой в отрезках вида или уравнение прямой с угловым коэффициентом легко приводятся к общему уравнению прямой, откуда и находятся координаты нормального вектора этой прямой.

Пример.

Найдите координаты нормального вектора прямой .

Решение.

От уравнения прямой в отрезках очень легко перейти к общему уравнению прямой: . Следовательно, нормальный вектор этой прямой имеет координаты .

Ответ:

Если прямую определяет каноническое уравнение прямой на плоскости вида или параметрические уравнения прямой на плоскости вида , то координаты нормального вектора получить немного сложнее. Из этих уравнений сразу видны координаты направляющего вектора прямой — . Найти координаты нормального вектора этой прямой позволяет условие перпендикулярности векторов и .

Также можно получить координаты нормального вектора прямой, если привести каноническое уравнение прямой или параметрические уравнения прямой к общему уравнению. Для этого производят следующие преобразования: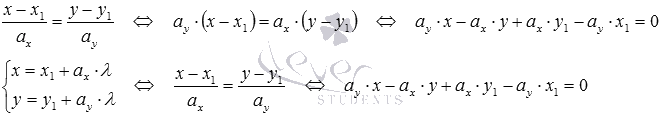

Как способ предпочесть – решать Вам.

Покажем решения примеров.

Пример.

Найдите какой-нибудь нормальный вектор прямой .

Решение.

Направляющим вектором прямой является вектор . Нормальный вектор прямой перпендикулярен вектору , тогда скалярное произведение векторов и равно нулю: . Из этого равенства, придав n_x произвольное ненулевое действительное значение, найдем n_y. Пусть n_x=1, тогда , следовательно, нормальный вектор исходной прямой имеет координаты .

Второй способ решения.

Перейдем от канонического уравнения прямой к общему уравнению: 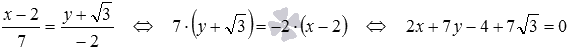. Теперь стали видны координаты нормального вектора этой прямой .

Ответ:

или

Пример.

Укажите координаты какого-либо нормального вектора прямой, заданной параметрическими уравнениями .

Решение.

Перейдем к общему уравнению этой прямой. Для этого выполним следующие действия: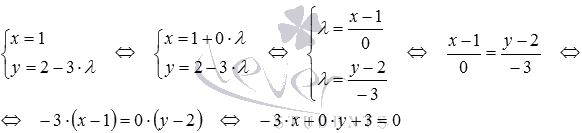

Теперь видны координаты нормального вектора прямой: .

Ответ:

Осталось рассмотреть способы нахождения координат нормального вектора прямой, которую определяют некоторые уравнения прямой в пространстве в прямоугольной системе координат Oxyz.

Если прямая задана уравнениями двух пересекающихся плоскостей и , то ее нормальным вектором является как нормальный вектор плоскости , так и нормальный вектор плоскости , то есть, векторы и .

Если прямую определяют канонические уравнения прямой в пространстве вида или параметрические уравнения прямой в пространстве вида , то числа a_x, a_y и a_z являются координатами направляющего вектора этой прямой. Нормальным вектором такой прямой является любой ненулевой вектор, перпендикулярный вектору . Таким образом, чтобы найти координаты нормального вектора прямой, заданной параметрическими или каноническими уравнениями в пространстве, нужно .

Список литературы.

• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

Некогда разбираться?

What Is a Norm?

A norm is a way to measure the size of a vector, a matrix, or a tensor. In other words, norms are a class of functions that enable us to quantify the magnitude of a vector. For instance, the norm of a vector X drawn below is a measure of its length from origin.

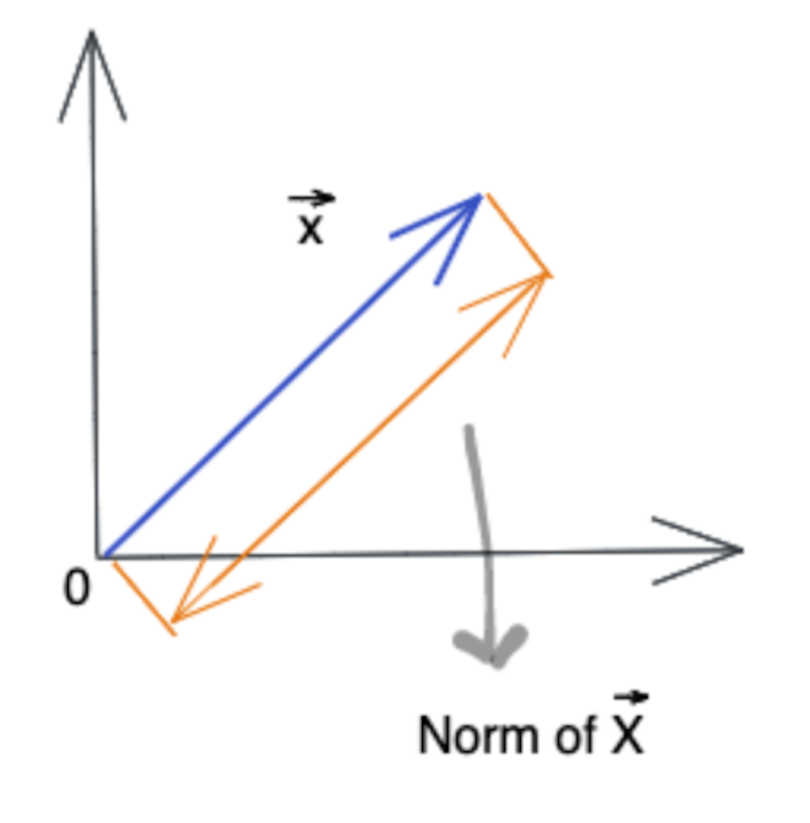Image created by the author.

The subject of norms comes up on many occasions in the context of machine learning:

• When defining lossfunctions, i.e., the distance between the actual and predicted values
• As a regularization method in machine learning, e.g., ridge and lasso regularization methods.
• Even algorithms like SVM use the concept of the norm to calculate the distance between the discriminant and each support-vector.

Примеры применения нормирования векторов в реальных задачах

1. Машинное обучение и анализ данных

Нормирование векторов является неотъемлемой частью обработки признаков в алгоритмах машинного обучения и анализа данных. Например, в задачах классификации объектов необходимо нормализовать значения признаков, чтобы они имели одинаковый масштаб и не приводили к несбалансированным весам в модели.

2. Графический дизайн и обработка изображений

Нормализация векторов также применяется в области графического дизайна и обработки изображений. Например, при работе с изображениями с высоким контрастом цветов, необходимо нормализовать цветовую гамму для создания более естественного визуального эффекта.

3. Физика и механика

Нормирование векторов используется во многих областях физики и механики. Например, в задачах международных стандартов единиц измерения давления, скорости или силы, можно использовать нормированные векторы для унификации данных.

4. Биоинформатика и молекулярная биология

Нормализация векторов является ключевым понятием в области биоинформатики и молекулярной биологии. Например, при работе с последовательностями ДНК необходимо проводить нормализацию данных для исключения влияния различий в длине последовательностей.

5. Финансы и экономика

Нормирование векторов может применяться в банковской и экономической сферах. Например, нормализация финансовых показателей позволяет унифицировать данные между компаниями разного размера и масштабов деятельности для проведения анализа финансовой устойчивости и прогнозирования будущих результатов.