Практическое применение понятия плоскости
Понятие плоскости играет важную роль в различных сферах нашей жизни. Вот некоторые примеры практического применения плоскости:
- Строительство: плоскость используется в строительстве для создания планов зданий, дизайна интерьера и экстерьера. Архитекторы и инженеры используют плоскость для расчетов, измерений и построения масштабных моделей.
- География: плоскость используется для создания карт и планов местности. Карты позволяют нам изучать и навигировать по различным областям и маршрутам.
- Мода: плоскость используется для создания выкройки и моделирования одежды. Дизайнеры используют плоскость для создания шаблонов и форм для дальнейшего пошива.
- Графика и дизайн: плоскость используется для создания иллюстраций, арт-работ и дизайна различных объектов, таких как логотипы, баннеры и упаковка товаров.
- Игры и развлечения: плоскость используется в различных играх, таких как шашки, шахматы и простые головоломки, где игроки могут перемещать объекты на плоскости по определенным правилам.
Это лишь некоторые примеры, как понятие плоскости применяется в реальном мире. Понимание плоскости позволяет нам анализировать и взаимодействовать с окружающей нас средой, а также создавать и проектировать новые объекты и структуры.
Как задать плоскость в пространстве
На уроках геометрии учитель может спросить: «А каким образом можно задать плоскость?», и некоторые из ваших одноклассников растеряются. Давайте разберемся, что значит «задать плоскость». По сути, это значит перечислить элементы и способы их расстановки, которые позволяют сказать: «Вот, через них проходит плоскость». Теперь подробнее разберемся, в каких случаях можно утверждать, что плоскость существует.
-
Вернемся к аксиоме. Как мы уже знаем, через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. А значит, задать плоскость можно через три точки, которые не лежат на одной прямой.
-
Второй способ вытекает из первого: проведем прямую, соединяющую две точки из трех. Сейчас нашей плоскости принадлежат прямая и точка, не лежащая на ней. Они и задают плоскость.
-
Продолжим соединять точки. На этот раз соединим между собой любые две точки: пусть это будут А и В, А и С. Мы получим две прямые, которые пересекаются друг с другом. Это значит, что плоскость могут задать две пересекающиеся прямые.
-
Четвертый способ: плоскость могут задать прямые, параллельные друг другу.
Построение плоскости на плоскости
Построение плоскости на плоскости — это одна из задач геометрии, которая представляет собой визуализацию плоскости на уже имеющейся плоскости. Для выполнения этой задачи, необходимо знать основные свойства плоскости и уметь работать с геометрическими фигурами.
В контексте 5 класса, для построения плоскости на плоскости можно использовать следующий алгоритм:
- Выбрать на исходной плоскости две точки, которые будут определять направление плоскости.
- Провести прямую через эти две точки.
- Выбрать на этой прямой еще одну точку.
- Провести прямые через каждую из трех точек.
- Точка пересечения двух прямых, проведенных через первую и вторую точку, определит требуемую плоскость.
Например, чтобы построить плоскость на плоскости, можно выбрать точки A(2,2) и B(6,4). Проведя прямую через эти точки, выберем на ней точку C(4,6). Проведем прямые через точки A, B и C. Точка пересечения двух прямых, проведенных через точки A и B, определит требуемую плоскость.
| Точка | Координаты |
|---|---|
| A | (2,2) |
| B | (6,4) |
| C | (4,6) |
Определение плоскости
Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Проецирование плоских фигур. Пересечение плоских фигур
Плоской называют такую фигуру, все точки которой лежат в одной плоскости и ограничены линиями, составляющими контур этой фигуры. Простейшей плоской фигурой является многоугольник.
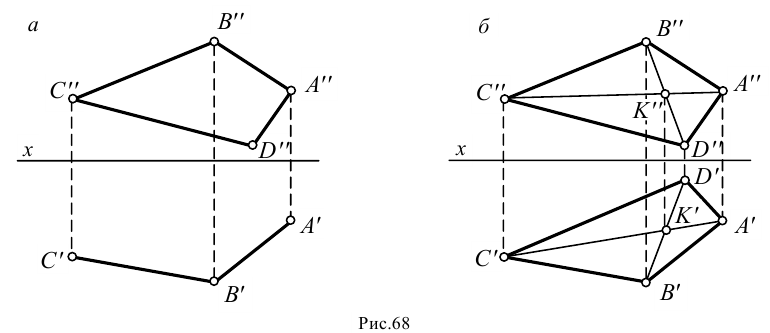
Для однозначного определения положения многоугольника в пространстве необходимо убедиться, чтобы все его точки находятся в одной плоскости.
Например, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис.68, а). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многогранника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей (рис.68, б).
Линия пересечения двух плоских фигур, как и линия пересечения двух плоскостей, определяется двумя точками, общими для этих фигур. Такие точки могут быть найдены как точки пересечения сторон одной фигуры с плоскостью другой.
На рис.69 найдена линия пересечения треугольников и . Для этого выполнены следующие построения.
Сначала найдена точка пересечения стороны треугольника с плоскостью треугольника . Затем аналогично построена точка пересечения другой стороны, например стороны , с плоскостью треугольника .
Для построения точки через сторону проведена вспомогательная фронтально-проецирующая плоскость и построена прямая пересечения вспомогательной плоскости и треугольника . На пересечении горизонтальных проекций и определена горизонтальная проекция точки встречи. Ее фронтальная проекция построена на фронтальной проекции .
Для построения точки через сторону проведена горизонтально-проецирующая плоскость . Затем построена прямая пересечения плоскости и треугольника и на пересечении с найдена фронтальная проекция . Точка построена на горизонтальной проекции .
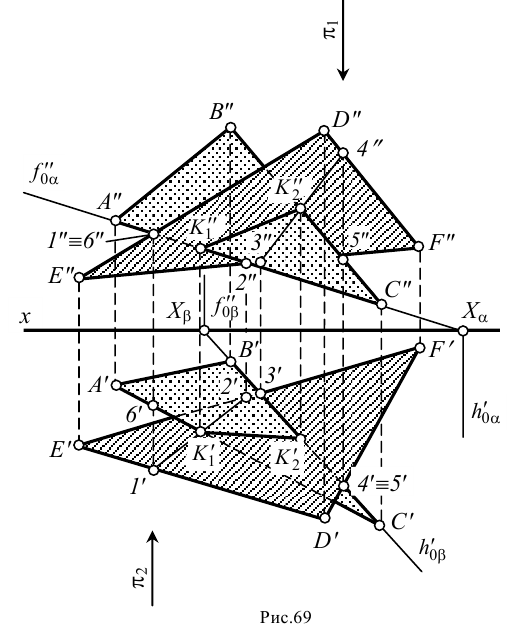
Зная две точки, общие для заданных плоскостей, проводим через них линию пересечения с проекциями и .
Определяем видимость плоскостей друг относительно друга с помощью конкурирующих точек, например, точек и — на горизонтальной плоскости проекций и точек и — на фронтальной плоскости проекций .
Пересекающиеся плоскости и угол между ними
Поскольку существует всего два варианта взаимного расположения плоскостей, то достаточно проверить, являются ли они параллельными или нет. В случае их пересечения часто возникает необходимость в определении соответствующего угла. Согласно определению, углом между рассматриваемыми геометрическими объектами является угол между их нормалями.
Таким образом, изучая вопрос взаимного расположения плоскостей и угла между плоскостями, достаточно рассчитать скалярное произведение векторов n1¯ и n2¯. Соответствующая формула примет вид:
Угол между плоскостями θ всегда является острым, поскольку в числителе стоит модуль скалярного произведения.
Следует отметить частный случай, когда две плоскости пересекаются под углом 90o. Тогда достаточно вычислить скалярное произведение нормальных векторов. Оно будет равным нулю.
Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат Охуz. Для определения нормального вектора n→=(A, B, C) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид Ax+By+Cz+D=0. То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2x-3y+7z-11=0.
Решение
По условию имеем уравнение плоскости
Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n→=(2, -3, 7) – это нормальный вектор плоскости
Все векторы плоскости задаются при помощи формулы t·n→=2·t, -3·t, 7·t, t является любым действительным числом не равным нулю.
Ответ: n→=(2, -3, 7).
Пример 2
Определить координаты направляющих векторов заданной плоскости x+2z-7=0.
Решение
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x+2z-7=0 к виду 1·x+0·y+2z-7=0. Отсюда получим, что координаты нормального вектора данной плоскости равны (1, 0, 2). Тогда множество векторов будет иметь такую форму записи (t, 0, 2·t), t∈R, t≠0.
Ответ: (t, 0, 2·t), t∈R, t≠0.
При помощи уравнения плоскости в отрезках, имеющего вид xa+yb+zc=1, и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1a, 1b, 1c.
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
- https://obrazovaka.ru/matematika/ploskost-pravilo.html
- https://budu5.com/manual/chapter/1216
- https://klevo.net/vzaimnoe-raspolozhenie-ploskostej-neobhodimye-svedenija/
- https://www.syl.ru/article/242597/mod_ploskie-i-obyemnyie-geometricheskie-figuryi
- https://ladle.ru/education/matematika/5class/ploskost-pryamaya
- https://Zaochnik.com/spravochnik/matematika/prjamaja-ploskost/normalnyj-vektor-ploskosti-koordinaty-normalnogo-v/
Плоскость в геометрии
В геометрии плоскость — это безграничная и без закруглений поверхность, которая может быть представлена как бесконечно маленькая аккуратная поверхность.
Некоторые свойства и особенности плоскости:
- Бесконечность: плоскость не имеет начала и конца, она простирается во все стороны.
- Гладкость: плоскость не содержит ни гребней, ни впадин, она абсолютно ровная и гладкая.
- Равенство всех прямых: любые две прямые, лежащие на плоскости, будут одинаковы в том смысле, что они не могут быть ни кривыми, ни загнутыми.
- Два измерения: плоскость имеет только два измерения — длину и ширину, не имея третьего измерения (высоты).
Примеры использования плоскости в повседневной жизни:
- Стол — это прямоугольная плоскость, на которой мы работаем и едим.
- Доска в школе — это плоскость, на которой пишут учителя и ученики.
- Окно — это прямоугольный фрагмент плоскости в стене, который позволяет проникать свету и воздуху в помещение.
В геометрии плоскости — это важный элемент для изучения различных фигур и форм, а также для работы с прямыми и точками.
| Свойство | Описание |
|---|---|
| Бесконечность | Плоскость не имеет начала и конца, она бесконечна во всех направлениях. |
| Гладкость | Плоскость не содержит никаких неровностей и отличается абсолютной ровностью. |
| Равенство всех прямых | Любые две прямые на плоскости будут иметь одинаковые свойства и не будут пересекаться. |
| Два измерения | Плоскость имеет только два измерения — длину и ширину. |
Теорема о трех перпендикулярах на плоскости
Чтобы прямая линия, которая лежит в данной плоскости, была к ней перпендикулярна, вполне достаточно, чтобы она была перпендикулярна к проекции данной плоскости.
Любой угол между линией и плоскостью — это угол между линией и ее выступом на плоскости. Когда прямая b наклонна к исходной плоскости, то прямая а будет проекцией этой наклонной, а угол α будет находиться между наклонной и заданной плоскостью.
Любая прямая, которая получена при пересечении 2 плоскостей, будет называться ребром двугранного угла. Полуплоскости с одним общим ребром называют треугольными угловыми гранями.
Если граница полуплоскости совпадает с краем двугранного угла и делит двугранный угол на два равных, то ее называют биссектрисой.
Угол с двойными стенками можно измерять соответствующим линейным углом. Линейный угол для любого двугранного угла является углом между перпендикулярами, проведенными к каждой грани, и ее краем.
Свойства плоскости
Плоскость — это геометрическая фигура, которая не имеет объема и расположена между двумя осями. Вот некоторые свойства плоскости:
- Плоскость проходит через любые три точки. Если даны три точки в пространстве, то всегда можно провести плоскость, через которую они все пройдут. Это свойство позволяет нам вычислять и строить плоскость, зная только несколько точек.
- Плоскость делит пространство на две части. Если есть плоскость в пространстве, то она разделяет пространство на две части: одна часть находится выше плоскости, а другая — ниже. Это свойство позволяет нам классифицировать точки и фигуры находящиеся с одной стороны плоскости или на другой стороне.
- Плоскость параллельна самой себе. Плоскость может быть параллельна самой себе, то есть располагаться на одном и том же расстоянии от другой плоскости. Параллельные плоскости никогда не пересекаются и имеют одинаковую ориентацию.
- Плоскость пересекается с прямой в одной точке или совпадает с прямой. Когда прямая пересекает плоскость, они могут встретиться только в одной точке или прямая может лежать полностью внутри плоскости. Если прямая лежит в плоскости, то они совпадают и имеют бесконечное количество общих точек.
Эти свойства плоскости помогают нам лучше понять и работать с этой геометрической фигурой. Они используются в различных задачах и приложениях, где требуется работа с плоскостью.
Параллельные плоскости
Теперь рассмотрим подробнее каждый из названных выше случаев. Предположим, что в общей форме заданы следующие две плоскости:
Как понять, являются ли они параллельными? Сделать это очень просто. Достаточно вспомнить о нормальных векторах. Если две плоскости параллельны между собой, значит, их нормали также параллельны. Выпишем координаты нормальных векторов к указанным плоскостям. Имеем:
Достаточным условием параллельности n1¯ и n2¯ является возможность задания одного из них через другой. Математически это записывается так:
Где k — некоторое (в том числе отрицательное) число. Если одну нормаль невозможно выразить путем умножения координат другой на число, то такие плоскости не будут параллельными.
Частным случаем параллельности плоскостей является их полное совпадение друг с другом. Тогда должны выполняться такие условия:
Пример параллельных плоскостей в пространстве приведен ниже.
Плоскость и ее основные свойства
Рассмотрим свойства плоскости, которые обычно принимаются без доказательств, поскольку это аксиомы:
- Когда каждые 2 точки, которые лежат на одной прямой, принадлежат к единой плоскости, то все точки, находящиеся на этой прямой, также будут принадлежать к данной плоскости.
- Если 2 плоскости соприкасаются в одной точке, значит они будут пересекаться на прямой линии, проходящей через эту точку.
- Для любых 3 точек, не принадлежащих одной прямой, можно нарисовать плоскость, причем только одну.
Последствия этих аксиом следующие:
- Можно нарисовать плоскость, имеющую прямую линию и точку за ней. Действительно утверждение, что точка вне прямой линии вместе с любыми двумя точками, лежащими на прямой, буду образовывать три точки, через которые может пройти новая плоскость.
- Через две пересекающиеся линии можно провести единственную плоскость. Если взять точку пересечения и еще одну точку на прямой, то получим 3 точки, через которые можно будет провести единственную плоскость.
- Только одну плоскость можно нарисовать двумя параллельными линиями. Доказано, что две параллельные прямые по определению лежат в одной плоскости. Эта плоскость уникальна, потому что не более одной плоскости можно провести через одну параллельную плоскость и одну точку в другую.
- Вращение плоскости по прямой. Поэтому можно провести бесчисленное количество плоскостей через любую линию в пространстве.
Доказательство:
- Действительно, пусть это будет прямая линия.
- Возьмите отдельно точку А.
- Через А и данную прямую а проходит плоскость М.
- Возьмем точку B, лежащую вне данной плоскости М.
- Через данную точку В и прямую линию также будет проходить плоскость N, которая может не совпадать с М. Это связано с тем, что она имеет точку B и она не принадлежит к М плоскости.
- Мы можем взять другую точку С в пространстве за плоскости М и N.
- Через точку С и прямой пройдет новая плоскость, например Р. Она не совпадет с М, ни с N, потому что содержит точку С, которая не принадлежит плоскости М и плоскости N.
Продолжая занимать все новые и новые точки в пространстве, мы получаем все больше и больше плоскостей. Они все будут пересекать исходную линию.
Их может быть бесчисленное число. Все полученные плоскости можно рассматривать как различные повороты одной исходной плоскости, которая может будет вращаться вокруг прямой А.
Таким образом, мы можем найти еще одно качество плоскости, которая может вращаться вокруг прямой, принадлежащей к ней.
Уравнение для плоскости, которая проходит через 3 точки
Если 3-мерном пространстве дана прямоугольная к-ная система, она обозначена обычно Oxyz.
Тогда уравнение, где данные a, b и C являются действительными числами больше нуля, именуется ур-ем плоскости на отрезки.
При абсолютном значении чисел a, b и с, они будут равны длине отрезков, обрезанных плоскостью по осям координат. Буквенные значения демонстрируют положительное или отрицательное направление линейных сегментов относительно оси координат.
Чтобы составить общее уравнение для исходной плоскости, можно применить следующую теорему.
Теорема:
Любое уравнение, имеющее стандартный вид, имеет действительные значения A, b, C и D, которые не должны быть равны нулю. Эти данные определяют исходную плоскость в системе координат Oxyz, расположенной в 3-мерном пространстве.
Эта теорема содержит в себе 2 части:
- Сначала получаем общее уравнение для плоскости, которая будет проходить через точку и саму плоскость.
- Затем мы доказываем, что данное уравнение можно использовать для действительных чисел, чтобы доказать, что оно будет определять плоскость V, Z и D.
Доказательство 1 части:
- Так как значения чисел A, V и Z не будут равны нулю одновременно, значит есть определенная точка, координаты которой будут соответствовать исходному уравнению, то есть выдавать верное равенство.
- Далее вычитаем правую и левую части полученного уравнения из данного уравнения. Получается уравнение, которое будет эквивалентно исходному.
- Далее необходимо будет доказать, что полученное уравнение будет определять именно плоскость в данной системе координат 3-мерного пространства и найти общее уравнение.
Главным условием для перпендикулярности 2 векторов является их равенство. То есть, когда координаты удовлетворяют уравнению, то векторы будут перпендикулярны и наоборот. При верном равенстве набор точек будет обуславливать плоскость, проходящую через эту точку.
Полученное уравнение будет определять плоскость, расположенную в 3-мерном пространстве. Также оно будет полностью соответствовать для общего уравнения плоскости, которая проходит через три точки.
Из сказанного следует, что любое уравнение, эквивалентное исходному, будет определять одну и ту же плоскость. Мы доказали 1 часть теоремы.
Доказательство 2 части теоремы:
Когда имеем плоскость, проходящую через точку, вектор которой нормален, мы можем доказать, что в прям-ной координатной системе Oxyz ее задают с помощью данного основного уравнения.
Если взять любую точку данной системы координат, то векторы будут перпендикулярны, а произведение будет равно нулю.
После принятия данного понятия, уравнение снова изменится и будет определять нашу плоскость.
Вывод: если уравнения эквивалентны, то они определяют одинаковую плоскость. Мы доказали теорему.
Данный обзор будет полезен при решении математических задач, а также в аналитической геометрии.
Сечения
Как дракон с помощью сечений разрушал город?
…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.
Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.
Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.
Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.
Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.
Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.
Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.
Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях
Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости
Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.
Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии
В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Зачем может потребоваться сечение? Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.
Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.
А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.
| Чем вода похожа на сечение?Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться. |
Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.
Взаимно перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.
Рассмотрим построение плоскости , перпендикулярной плоскости и проходящей через прямую (рис.73). Из любой точки прямой , например из точки , проводим перпендикуляр к заданной плоскости . Строим проекции следов прямой и перпендикуляра .
Через горизонтальные проекции горизонтальных следов и проводим горизонтальный след плоскости ; через фронтальные проекции фронтальных следов и — ее фронтальный след. Проверяем правильность построений: следы и пересекаются в точке схода следов , на оси .
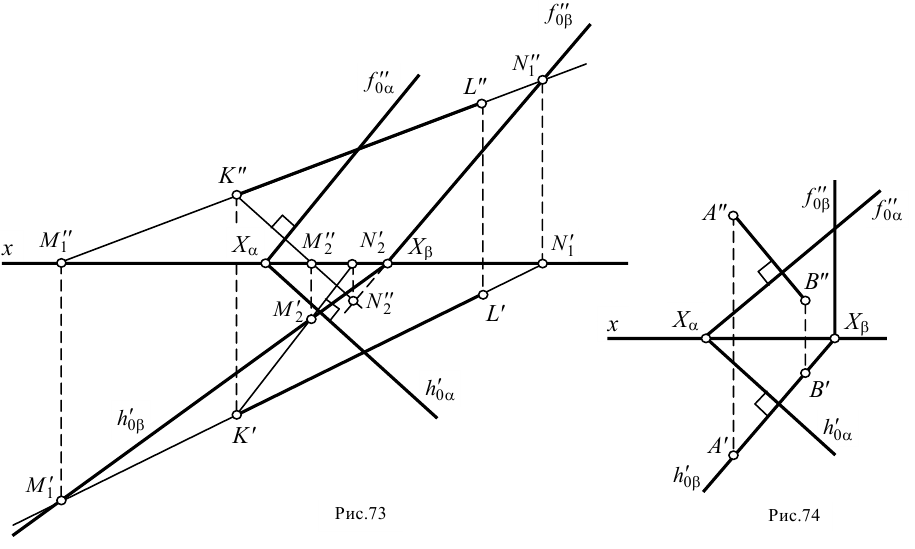
Таким образом, плоскость перпендикулярна плоскости , так как проходит через прямую , перпендикулярную плоскости
Следует обратить внимание на то, что одноименные следы плоскостей и не перпендикулярны друг другу
Действительно, одноименные следы двух взаимно перпендикулярных плоскостей общего положения не перпендикулярны друг другу. Наоборот, если одноименные следы двух плоскостей общего положения взаимно перпендикулярны, то сами плоскости не перпендикулярны между собой.
Если одна из рассматриваемых плоскостей является плоскостью частного положения, то существует несколько очевидных случаев, когда перпендикулярность следов может служить признаком перпендикулярности самих плоскостей. Например, перпендикулярность горизонтальных следов плоскости общего положения а и горизонтально-проецирующей плоскости соответствует взаимной перпендикулярности этих плоскостей (рис.74). Это нетрудно доказать, выбрав в плоскости прямую , перпендикулярную плоскости .
По аналогии с рассмотренным примером перпендикулярность фронтальных следов фронтально-проецирующей плоскости и плоскости общего положения также соответствует взаимной перпендикулярности этих плоскостей.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Взаимное расположение точки, прямых и плоскостей
- Перпендикулярность геометрических объектов
- Метод замены плоскостей проекций
- Проецирование прямой линии
- Поверхности вращения
- Пересечение прямой линии с поверхностью
- Построение линии пересечения поверхностей
- Проецирование прямой




























