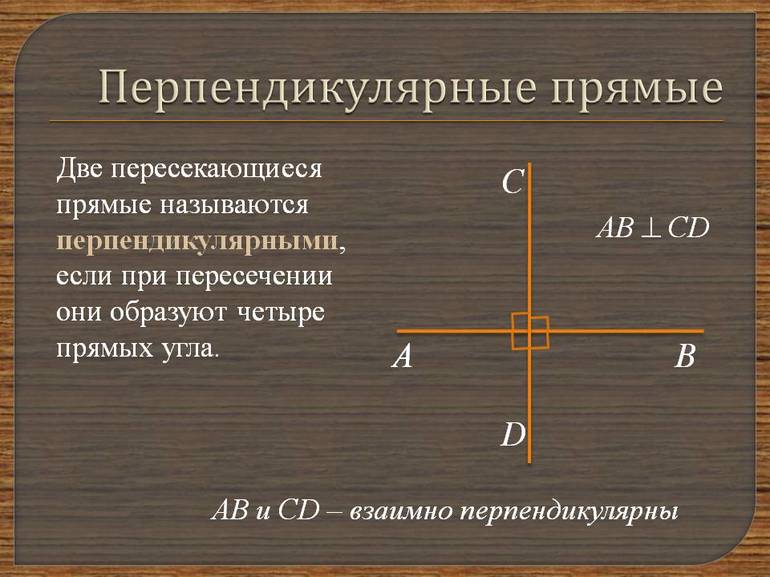
Шаг 1: Перпендикулярность: определение и свойства
Основное свойство перпендикулярных прямых заключается в том, что угол между ними равен 90 градусам. Это значит, что когда две перпендикулярные прямые пересекаются, они образуют прямой угол.
Перпендикулярные прямые обладают следующими свойствами:
| Свойство | Описание |
| Определение | Две прямые называются перпендикулярными, если они пересекаются под прямым углом. |
| Угол | Угол между перпендикулярными прямыми равен 90 градусам. |
| Существование | Для любой данной прямой существует единственная перпендикулярная ей прямая. |
| Симметрия | Если прямая A перпендикулярна прямой B, то прямая B также перпендикулярна прямой A. |
| Третья прямая | Если прямая A перпендикулярна прямой B, и прямая B перпендикулярна прямой C, то прямая A также перпендикулярна прямой C. |
Примеры перпендикулярных прямых включают:
— Вертикальные линии, такие как стены в здании, которые пересекают горизонтальные полы или потолки.
— Углы треугольников, где перпендикулярные прямые соответствуют боковым сторонам.
— Линии на карте, которые пересекают друг друга в прямых углах.
Понимание понятия перпендикулярности и его свойств поможет в решении задач геометрии, а также в построении и анализе различных фигур и объектов.
Геометрическое определение перпендикулярности
Геометрическое определение перпендикулярности можно проиллюстрировать на примере перпендикулярных отрезков. Если два отрезка пересекаются так, что образуется прямой угол, то они являются перпендикулярными. Данное определение также применимо к отрезкам, лучам и прямым линиям. Примером перпендикулярных прямых могут служить стороны прямоугольника или крест-анкер, где четыре прямые линии образуют углы в 90 градусов друг с другом.
Понятие перпендикулярности широко используется в геометрии и играет важную роль в решении различных задач. Например, перпендикулярные линии и плоскости часто используются для построения прямоугольных форм, ориентации объектов в пространстве и определения правильных углов. Знание определения перпендикулярности позволяет точно определить взаимное расположение линий и применять их в практических ситуациях.
Свойства перпендикулярных линий и отрезков
Одним из главных свойств перпендикулярных линий является то, что они образуют прямой угол. Прямой угол равен 90 градусам и может быть обозначен символом ⌫. Если две линии пересекаются и образуют прямой угол, то они называются перпендикулярными.
Еще одним свойством перпендикулярных линий и отрезков является то, что они имеют равные углы косинусы. Если две линии перпендикулярны, то косинусы углов, образованных этими линиями, равны 0. Это свойство может быть использовано для нахождения перпендикулярной линии или отрезка.
Еще одно важное свойство перпендикулярных линий и отрезков — то, что они не пересекаются. Если две линии пересекаются, то они не могут быть перпендикулярными. Это свойство помогает строить перпендикуляры и определять их положение в пространстве
Это свойство помогает строить перпендикуляры и определять их положение в пространстве.
Кроме того, перпендикулярные линии и отрезки могут использоваться для создания прямоугольников, параллелограммов и других геометрических фигур.
Итак, свойства перпендикулярных линий и отрезков — это образование прямого угла, равность углов косинусов, их непересечение и использование в построении различных фигур. Знание этих свойств поможет решать задачи и проводить геометрические конструкции.
Понятие взаимной перпендикулярности
Другими словами, если имеются две перпендикулярные линии А и В, и две перпендикулярные линии С и D, то можно сказать, что А перпендикулярна В, С перпендикулярна D, и А перпендикулярна С, и В перпендикулярна D. Таким образом, все линии в данной системе взаимно перпендикулярны друг другу.
Примером взаимной перпендикулярности может служить прямоугольник. В прямоугольнике все четыре стороны являются взаимно перпендикулярными, так как каждая из них образует прямой угол с соседними сторонами.
Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Интересная задача
Есть такая задача:В Заколдованном Лесу било 10 заколдованных источников — номер 1, 2, 3,… 10. Вода каждого источника была неотличима на цвет, вкус и запах от обычной воды, но являлась сильнейшим ядом. Выпивший её был обречён — если только в течение часа после этого не пил воды источника с бОльшим номером (например, от яда источника 3 спасали источники 4-10; яд 10-го источника не оставлял шансов на спсасение). Первые 9 источников были общедоступны, но источник 10 был в пещере Кащея Бессмертного, и доступ к нему имел только Кащей.И вот однажды Иван-Дурак вызвал Кащея на поединок. Условия были простыми: каждый приносит с собой по стакану некоторой жидкости, соперники обмениваются стаканами и выпивают их содержимое. А дальше — справляются, как могут.Кащей был доволен. Ещё бы: он даст Ивану яд номер 10, и Ивана ничто не сможет спасти. А сам он яд, данный Иваном, запьёт водой 10-го источника — и будет спасён.Попробуйте разработать план дуэли для Ивана. Задача — остаться жить самому и прикончить Кащея.Ответ 1. Угробить Кащея. Ему нужно дать не яд, а чистую воду. Он запьёт её своим ядом — и он обречён.Ответ 2. Не угробиться самому. Любой яд, кроме номера 1, может являться и противоядием. Перед тем, как придти на дуэль, нужно выпить яд малого номера. И тогда яд номер 10, полученный от Кащея на дуэли, не убьёт, а спасёт.Вообще, идея-то тривиальная. Не всегда можно взвесить поступок изолированно. Одно и то же действие может оказаться и ядом, и противоядием. Многое зависит от фона. Не буду говорить, что всё — но, несомненно, многое.И когда вы слышите, что кто-то из ваших знакомых совершил Такую-То и Такую-То Гадости, не спешите вешать ярлыки. Уверены ли вы, что это именно гадости? Не может ли быть, что они просто выглядят так? Уверены ли вы, что фон этих действий вам известен?
Применение термина
Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.
В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.
В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.
Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.
Определение перпендикулярности прямой и плоскости
Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.
Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:
- Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
- В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.
Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.
В трехмерном пространстве
Перпендикулярные линии
Две прямые в пространстве перпендикулярны тогда и только тогда, когда они пересекаются под прямым углом. В космосе непараллельные линии могут не пересекаться. Если одна из линий параллельна прямой, перпендикулярной другой, то две прямые называются ортогональными . Они будут называться перпендикулярными, только если они секущие.
В пространстве, если дана линия и указана точка, не находящаяся на линии, есть только одна линия, проходящая через данную точку и перпендикулярную данной линии. Если точка расположена на прямой, через эту точку проходит бесконечное количество прямых, перпендикулярных данной прямой.
В космосе понятия параллелей и перпендикуляров больше не связаны.
- Если две прямые перпендикулярны, любая линия, параллельная одной, ортогональна только другой. Оно будет перпендикулярно другому, только если оно разрезает его.
- Если две прямые параллельны, любая прямая, перпендикулярная одной, ортогональна только другой. Он будет перпендикулярен другому только в том случае, если он его разрежет.
- Две прямые могут быть перпендикулярны одной и той же линии, но не параллельны, достаточно, например, взять три линии, поддерживающие края угла куба .
Линия, перпендикулярная плоскости
В пространстве, если линия не параллельна плоскости, она всегда пересекает эту плоскость. Если линия перпендикулярна двум пересекающимся линиям плоскости, мы будем говорить, что линия перпендикулярна плоскости. Тогда линия будет ортогональна всем линиям плоскости. Это свойство иногда называют теоремой о двери, потому что оно объясняет, почему дверь может поворачиваться на петлях, если ее ось вращения перпендикулярна полу.
В пространстве через данную точку проходит только одна линия, перпендикулярная данной плоскости, и только одна плоскость, перпендикулярная данной линии.
Затем мы находим более интересные отношения на перпендикулярном и параллельном
- Если линия перпендикулярна плоскости, любая линия, параллельная первой, также перпендикулярна плоскости, любая плоскость, параллельная переднему плану, также перпендикулярна прямой.
- Если две прямые параллельны, любая плоскость, перпендикулярная одной, перпендикулярна другой. Если две плоскости параллельны, любая линия, перпендикулярная одной, перпендикулярна другой.
- Если две плоскости перпендикулярны одной и той же линии, они параллельны. Точно так же, если две прямые перпендикулярны одной плоскости, они параллельны.
Направление, перпендикулярное поверхности в точке, часто называют направлением, нормальным к поверхности , или же ортогональным .
Перпендикулярные плоскости
Представление о перпендикулярных плоскостях, хотя и интуитивно понятно, очень опасно, поскольку практически не имеет свойств. Чтобы понять понятие перпендикулярных плоскостей, мы должны вернуться к первому определению перпендикуляра ( отвес ) и к понятиям вертикальной плоскости и горизонтальной плоскости . Горизонтальная плоскость — это плоскость, перпендикулярная направлению отвеса. Вертикальная плоскость — это плоскость, содержащая направление отвеса. Тогда говорят, что вертикальная плоскость перпендикулярна горизонтальной плоскости.
Из этого первого понятия рождается следующее определение: плоскость перпендикулярна другой, если она содержит линию, перпендикулярную второй плоскости. Докажем, что это соотношение симметрично.
Нет понятия ортогональных плоскостей в размерности 3. Две плоскости были бы ортогональными, если бы любое направление переднего плана было ортогональным любому направлению второй плоскости, что материально невозможно.
Мы должны опасаться понятия перпендикулярных плоскостей. Например :
- две перпендикулярные плоскости могут содержать параллельные линии
- две плоскости, перпендикулярные третьей, не обязательно параллельны (см. грани куба ).
Однако есть еще некоторые свойства
- Если две плоскости перпендикулярны, плоскость, параллельная одной, перпендикулярна другой.
- Если две плоскости параллельны, плоскость, перпендикулярная одной, перпендикулярна другой.
📽️ Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

10 класс, 18 урок, Теорема о прямой, перпендикулярной к плоскостиСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Геометрия 10 класс (Урок№9 — Признак перпендикулярности прямой и плоскости.)Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Геометрия 10 класс (Урок№10 — Перпендикуляр и наклонные.)Скачать

Уравнения прямой на плоскости | Векторная алгебраСкачать
Как составить уравнение прямой, проходящей через две точки. Урок 3. Геометрия 8 класс.Скачать

Условие перпендикулярности векторов. 11 класс.Скачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

Составляем уравнение прямой по точкамСкачать

7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Свойства перпендикулярных углов
Перпендикулярные углы обладают несколькими важными свойствами:
1. Перпендикулярные углы равны между собой. Если две прямые линии пересекаются и образуют перпендикулярные углы, то их величины будут одинаковыми.
2. Сумма двух перпендикулярных углов равна 90 градусов. Если две прямые линии пересекаются и образуют перпендикулярные углы, то сумма этих углов будет составлять 90 градусов.
3. Перпендикулярные углы образуются между пересекающимися перпендикулярными прямыми. Если две прямые линии пересекаются и образуют перпендикулярные углы, они будут также пересекать другие прямые и образовывать перпендикулярные углы.
4. Прямые линии, перпендикулярные одной и той же прямой, образуют пары перпендикулярных углов. Если прямая и имеющаяся прямая образуют перпендикулярные углы, то пары углов, образованные другими прямыми пересекающимися с этой прямой, будут также являться перпендикулярными углами.
Перпендикулярные углы являются важным понятием в геометрии и часто используются для решения задач, связанных с прямыми, плоскостями и углами.
Сумма перпендикулярных углов
Перпендикулярные углы обладают особыми свойствами, включая свойство суммы. Сумма двух перпендикулярных углов всегда равна 90 градусам.
Предположим, у нас есть две перпендикулярные прямые, пересекающиеся в точке O. Вертикальные углы, образованные этими прямыми, являются перпендикулярными углами. Угол AOB и угол COD — перпендикулярные углы. Их сумма равна 90 градусам.
Пример:
На чертеже дома имеется перпендикулярный угол, образованный стенами. Угол между стенами А и В равен 40 градусам, а угол между стенами В и С равен 50 градусам. Тогда сумма этих двух перпендикулярных углов будет равна 90 градусам (40 градусов + 50 градусов = 90 градусам).
Свойство суммы перпендикулярных углов можно использовать для решения различных геометрических задач и нахождения неизвестных углов.
Дополнительные углы
Свойства дополнительных углов позволяют решать различные геометрические задачи. Например, если у нас есть два угла, и мы знаем, что они являются дополнительными, то можем найти значение одного угла, если известно значение другого.
Ниже приведены некоторые примеры:
- Угол A = 40°, угол B — дополнительный к углу A. Найдем значение угла B:Угол B = 180° — 40° = 140°
- Угол X = 120°, угол Y — дополнительный к углу X. Найдем значение угла Y:Угол Y = 180° — 120° = 60°
- Угол M = 80°, угол N — дополнительный к углу M. Найдем значение угла N:Угол N = 180° — 80° = 100°
Также важно отметить, что дополнительные углы могут быть как острыми, так и тупыми. Главное условие — их сумма должна быть равна 180 градусам
Знание о дополнительных углах помогает решать задачи связанные с измерением и сравнением углов, а также строить и анализировать геометрические фигуры.
Равные перпендикулярные углы
Например, если взять две перпендикулярные линии AB и CD, и на них построить перпендикулярные углы AEF и CEG, то эти углы будут равны друг другу. В случае равенства перпендикулярных углов возникает возможность решения разнообразных уравнений и геометрических задач, таких как построение фигур или нахождение неизвестных углов и сторон.
Равные перпендикулярные углы — одно из основных свойств перпендикулярных линий и широко используется в геометрии. Это позволяет упростить решение задач и делает их более понятными и доступными.
Свойства перпендикулярных прямых
Сначала разберём два «стандартных» свойства, которые вы найдёте в любом учебнике геометрии 7-го класса. А затем — одно «нестандартное», но именно оно чаще всего и встречается в настоящих задачах.
3.1. Теорема о двух прямых, перпендикулярных третьей
Прямая $AB\bot EF$ и прямая $MN\bot EF$. Следовательно, прямые $AB$ и $MN$ не пересекаются. Проще говоря, они параллельны (см. урок «Параллельные прямые»).
3.2. Теорема о прямой, перпендикулярной данной
Доказательство этой теоремы состоит из двух частей: сначала докажем, что такую прямую провести можно, а затем — что она единственная.
Прямая, перпендикулярная данной, строится очень просто. Рассмотрим прямую $a$, на которой отмечена точка $M$:
Отложим от луча $MK$ угол, равный 90°. В любую сторону: в верхнюю полуплоскость или нижнюю — не имеет значения. Получим луч $MN$:
Наконец, продолжим луч $MN$ в противоположную другую сторону (т.е. построим дополнительный луч). Получим искомую прямую $MN\bot a$:
Единственность такого построения следует либо из аксиомы о том, что нужный угол можно отложить в нужном направлении одним и только одним способом, либо из предыдущей теоремы о двух прямых, перпендикулярных данной. В самом деле, пусть есть ещё одна прямая $ML$, которая, как и $MN$, перпендикулярна прямой $a$:
Поскольку $MN\bot a$ и $ML\bot a$, по предыдущей теореме эти прямые не пересекаются. Что противоречит нашему построению, в котором у прямых $MN$ и $ML$ есть общая точка $M$. Следовательно, прямые $MN$ и $ML$ совпадают, что и требовалось доказать.
3.3
Важное свойство прямого угла. Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи
Звучит оно очень просто:
Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:
Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:
Это утверждение может показаться очевидным. И оно действительно является таковым. Однако деление прямого угла на части встречается в задачах настолько часто, что я не мог не упомянуть об этом.
Кроме того, начинающие ученики часто не замечают такие углы на чертежах. Поэтому сейчас мы будем отрабатывать эту теорему на реальных задачах.
Перпендикулярность и косинусы в математике
В геометрии перпендикулярность — это особый вид отношения между двумя прямыми, лучами или отрезками. Два отрезка, луча или прямые называются перпендикулярными, если они образуют прямой угол, то есть угол, равный 90 градусам.
Перпендикулярность имеет несколько основных свойств:
- Перпендикулярные прямые или отрезки никогда не пересекаются.
- Перпендикулярные прямые или отрезки имеют равные прямые углы между ними.
- Если два отрезка или луча перпендикулярны к одной прямой, они также перпендикулярны друг другу.
Для определения перпендикулярности применяются различные методы. Однако наиболее популярным является применение тригонометрических функций и величины косинуса.
Косинус угла между двумя векторами или прямыми определяется по формуле:
| cos(θ) = a · b / (|a| · |b|) |
|---|
Где a и b — это два вектора или прямые, |a| и |b| — длины этих векторов или прямых, а θ — угол между ними.
Если косинус угла между двумя векторами или прямыми равен 0, это означает, что они перпендикулярны друг другу.
Применение косинусов позволяет более точно и удобно определять перпендикулярность в геометрии и математике в целом. Также косинусы широко используются в различных научных и инженерных расчетах.
Свойство перпендикулярных прямых
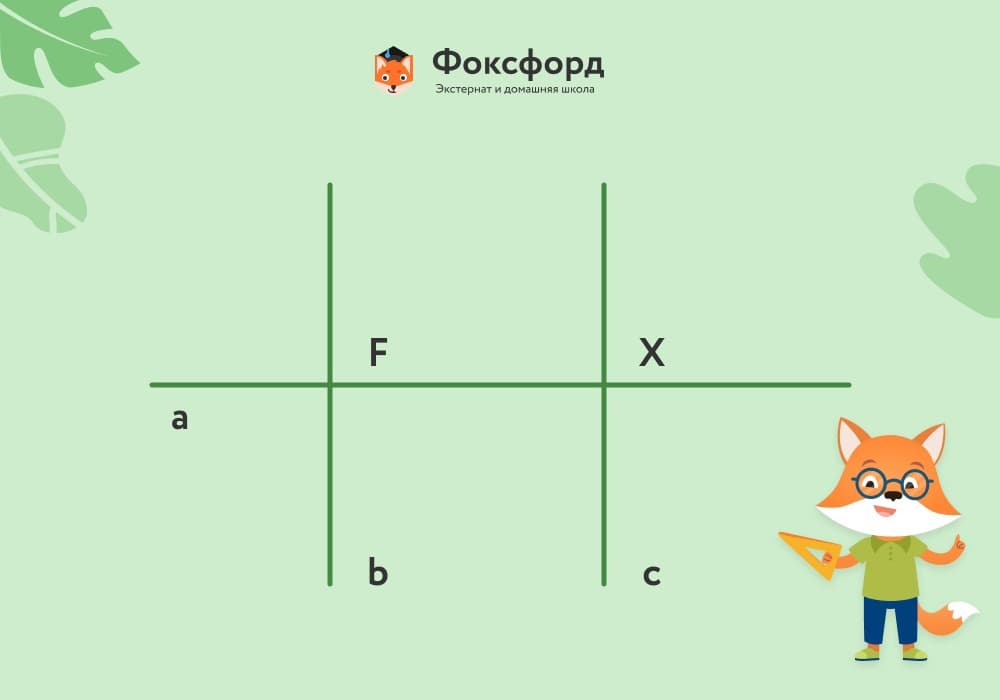
Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.


Мы в инстаграм
Домашняя онлайн-школаПомогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством
Звонок по России бесплатный
Посмотреть на карте
Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.
Теорема о перпендикулярных прямых, как доказать
Задачи на перпендикулярные прямые, как правило, решают с учетом свойств этих линий. Доказательством перпендикулярности прямых является прямой угол, который они составляют. В том случае, когда требуется определить их перпендикулярность при известных уравнениях прямоугольной системы координат, следует применить необходимое и достаточное условие перпендикулярности линий.
Теорема 1
Теорема 1
Для того чтобы прямые a и b являлись перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.
Подтверждением данной теоремы является определение направляющего вектора прямой и перпендикулярности линий.
Допустим, что имеется прямоугольная декартовая система координат Оху, на которой заданы уравнения для прямой на плоскости, определяющие линии а и b. Направляющие векторы, характерные для данных прямых а и b, можно обозначить, как:
\(\vec{a}\) и \(\vec{b}\)
Согласно формуле прямых а и b, необходимым и достаточным условием является перпендикулярность векторов \(\vec{a}\) и \(\vec{b}.\)
Данное утверждение справедливо в том случае, когда скалярное произведение векторов:
\(\vec{a}=(a_{x};a_{y})\) и \(\vec{b}=(b_{x};b_{y})\) не равно нулю, а запись обладает таким видом:
\((\vec{a};\vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0\)
Таким образом, необходимое и достаточное условие перпендикулярности линий а и b, которые расположены в прямоугольной системе координат Оху на плоскости, представляет собой следующее выражение:
\((\vec{a};\vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0\)
где \(\vec{a}=(a_{x};a_{y})\) и \(\vec{b}=(b_{x};b_{y})\) являются направляющими векторами линий а и b.
Данную теорему целесообразно использовать в том случае, когда требуется определить координаты направляющих векторов, либо, когда известны канонические или параметрические уравнения прямых на плоскости заданных линий а и b.
Примечание
Необходимое и достаточное условие перпендикулярности прямых а и b можно применять в случае трехмерного пространства.
В данном отношении запись будет иметь такой вид:
\((\vec{a};\vec{b})=a_{x}*b_{x}+a_{y}*b_{y}+ a_{z}*b_{z}=0\)
где \(\vec{a}=(a_{x};a_{y})\)
\(\vec{b}=(b_{x};b_{y})\)
\(\vec{z}=(z_{x};z_{y})\)
являются направляющими векторами прямых а и b.
Теорема 2
Теорема 2
Линии а и b на плоскости будут перпендикулярны, если нормальный вектор прямой а и вектор прямой b взаимно перпендикулярны. Данное условие считается необходимым и достаточным.
Доказательство этой теоремы заключается в применении рассматриваемого условия в том случае, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. Таким образом, имея общее уравнение прямой вида:\(
A_{x}+B_{y}+C=0\)
а также уравнение прямой в отрезках вида:
\(\frac{x}{a}+\frac{y}{b}=1\)
и уравнение прямой с угловым коэффициентом вида y = kx + b, координаты векторов можно определить.
В том случае, когда линия а на плоскости определена с помощью уравнения с угловым коэффициентом:
\(y=k_{1}x+b_{1}\)
и прямая b имеет вид:
\(y=k_{2}x+b_{2}\)
тогда координаты нормальных векторов будут следующие:
\((k_{1};-1)\) и \((k_{2};-1)\)
Условие перпендикулярности соответствует выражению:
\(k_{1}*k_{2}+(-1)*(-1)=0\Leftrightarrow k_{1}*k_{2}=-1\)
Теорема 3
Теорема 3
Прямые а и b перпендикулярны на плоскости при необходимом и достаточном условии, при котором один из направляющих векторов этих линий будет коллинеарным нормальному вектору второй прямой.
Доказательство взаимного расположения
Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:
- Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
- Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.
Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.
https://youtube.com/watch?v=7uOoLy6YKZY
Построение прямых углов на местности
Для построения прямых углов на местности применяют специальные приборы, простейшим из которых является экер. Экер представляет собой два бруска, расположенных под прямым углом и укрепленных на треножнике (рис. 7). На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны. Чтобы построить на местности прямой угол с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (прямая ОВ на рисунке 7). Получается прямой угол АОВ.В геодезии для построения прямых углов используются более совершенные приборы, например теодолит.
Задание.
По горизонтали:3. Отрезок прямой, соединяющий точку окружности с ее центром. 6. Утверждение, не требующее доказательства. 9. Конструкция, система мысли. 10. Вид четырехугольника. 15. Отрезок прямой, соединяющий две точки кривой. 16. Мера длины. 17. Тригонометрическая функция. 18. Точка пересечения диаметров окружности. 19. Тригонометрическая функция. 20. Часть окружности. 21. Старинная мера длины.По вертикали:1. Символ какого-либо алфавита. 2. Вид параллелограмма. 4. Хорда, проходящая через центр окружности. 5. Геометрический элемент. 7. Луч, делящий угол пополам. 8. Символ греческого алфавита. 10. Сумма длин сторон треугольника. 11. Вспомогательное предложение, используемое для доказательства. 12. Элемент прямоугольного треугольника. 13. Одна из замечательных линий треугольника. 14. Тригонометрическая функция.
Что такое перпендикулярно?
Перпендикуляры могут относиться к линиям, кривым, прямоугольникам или трехмерным фигурам. Они проходят перпендикулярно и пересекаются в определенной точке.
Точка пересечения является прямым углом для перпендикулярных фигур.
Перпендикулярность описывается или демонстрируется с помощью определенного символа. У них также есть собственное уравнение.
Это следует транзитивному свойству, согласно которому, если прямая X перпендикулярна прямой Y, которая перпендикулярна прямой Z, то прямая X становится перпендикулярной прямой Z.
Прямые углы или углы в девяносто градусов изображают перпендикулярные лучи. Они рассчитываются, измеряются и строятся с помощью теоремы Пифагора.
Эта теорема и метод используются при закладке нескольких полей, садов и других больших площадей.
Несколько примеров помогают нам понять перпендикулярные лучи и дают нам краткое представление об этом термине. Некоторые из этих примеров:
- Конструкции окна.
- Футбольное поле.
- Пересечения железнодорожных путей.
- Дом со стеной, лежащей перпендикулярно полу и потолку.
- Знак «плюс» аптечки или коробки.
Линии в этом случае точно вертикальные и прямые. Буква «Т» состоит из двух линий, лежащих перпендикулярно друг другу. Они лежат под прямым углом друг к другу.
Оптические условия
В оптике существуют определенные условия, которые определяют поведение световых лучей при распространении в среде. Изучение этих условий позволяет понять, почему перпендикулярный луч не преломляется и как такое явление объясняется.
Световой луч — это узкий параллельный пучок света, который обладает определенными свойствами при прохождении через различные оптические среды. Отражение и преломление — два основных процесса, которые определяют поведение лучей при переходе из одной среды в другую.
Один из оптических законов, известный как закон преломления, гласит, что при переходе луча из среды с одним показателем преломления в среду с другим показателем преломления, угол падения равен углу преломления. Это означает, что световой луч может изменять свое направление при взаимодействии с разными материалами.
Однако важно понимать, что перпендикулярный луч, падающий перпендикулярно границе раздела двух сред, не преломляется при переходе. Это происходит из-за того, что угол падения в данном случае равен нулю, а следовательно, угол преломления также равен нулю
Это и объясняет отсутствие преломления при взаимодействии перпендикулярного луча с поверхностью раздела сред.
|
Причиной такого поведения перпендикулярного луча может быть разница в оптической плотности разных сред. Оптическая плотность определяет скорость распространения света в среде и может варьироваться в зависимости от ее физических свойств. Интересное явление, связанное с оптическими условиями, это полное внутреннее отражение. Оно наблюдается при попытке преломления луча, падающего из более плотной среды в менее плотную, при условии, что угол падения превышает критический угол. В этом случае луч полностью отражается от границы раздела сред и не проникает в новую среду. |
Изменение показателя преломления
В ходе преломления света происходит изменение показателя преломления. Это явление сопровождается перераспределением энергии световых волн и изменением направления распространения света. При этом перпендикулярный луч, падающий на границу раздела двух сред, не преломляется в силу особенностей этого явления.
Перепад показателей преломления возникает вследствие различной связи фотонов с атомами в разных средах. Вещества имеют свои характеристики, включая показатель преломления, который определяет, насколько сильно свет изменяет свой курс при переходе из одной среды в другую.
Однако перпендикулярный луч, идущий под углом 90 градусов к поверхности раздела сред, не подвергается преломлению. В силу симметрии этого угла, покажется, что световая волна не изменит свое направление и сохранит первоначальный курс.
- Изменение показателя преломления связано с перераспределением энергии световых волн.
- Перпендикулярный луч, испытывая падение под прямым углом на границу раздела двух сред, не преломляется.
- Различные свойства веществ приводят к различному показателю преломления.
Как понять что перпендикуляр?
Перпендикулярные прямые на плоскости
В геометрии перпендикулярными называют прямые на плоскости, образующие четыре прямых угла при пересечении.
Ключевые особенности перпендикулярных прямых:
- Образуют прямой угол (90 градусов) при пересечении.
- Угол между ними равен π/2 радиан.
- Две перпендикулярные прямые делят плоскость на четыре части.
- Перпендикулярные прямые могут быть получены как ортогональные проекции одной прямой на другую.
- Историческая справка:
Устаревший термин для перпендикулярной прямой — «восставленная». Он возник от представления прямой, перпендикулярной к горизонтальной линии, как линии, поднятой вертикально.
Признаки параллельности прямых
По характерным углам, которые образуются секущей, можно определить параллельность прямых. Первый из признаков параллельности двух прямых звучит так:

Попробуем доказать это. Пусть c – секущая для aи b, и ∠1 равен∠5.
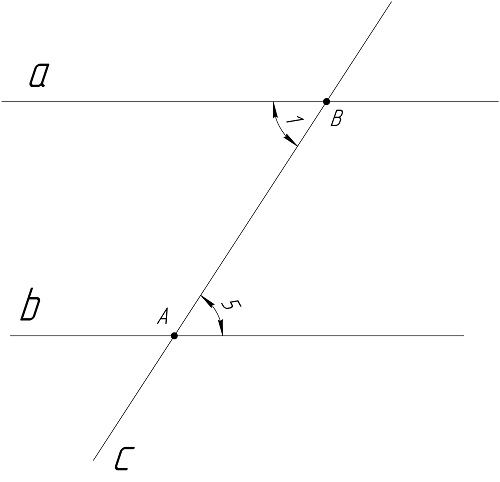
Сначала рассмотрим простейший случай, когда эти углы прямые. Тогда a и b перпендикулярны c,а потому a||b. В более сложном случае ∠1 и ∠5 не равны 90°. Тогда с середины отрезка АВ (обозначим ее как О), опустим перпендикуляр на a, а точку их пересечения обозначим как H. Далее построим отрезок АК, который лежит на b и равен по длине BH:
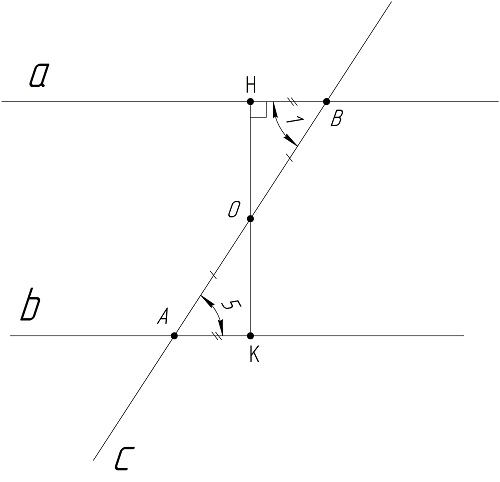
Теперь рассмотрим треугольники АОК и ВОН. ∠ОАК и ∠НВО равны друг другу, также равны и две прилегающие к нему стороны: ОА=ОВ (так как О – середина отрезка АВ) и HB=АК. Получаем, что эти треугольники равны друг другу по 1-ому признаку равенства треугольников (смотри урок 3).
Из этого можно сделать два вывода. Во-первых, равны ∠АОК и ∠НОВ, поэтому они являются вертикальными.Это означает, что Н, О и К располагаются на одной прямой. Во-вторых, угол ∠ОКА=∠ВНО=90°. Следовательно, отрезок HK перпендикулярен и к a, и к b. Поэтому a||b.
Второй признак формулируется так:

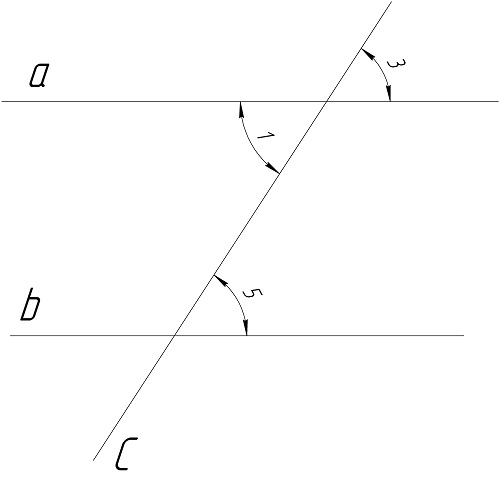
Действительно, пусть ∠3 и ∠5 равны друг другу. Тогда∠1 равен∠3, так как они вертикальные. Получаем, что ∠5=∠3=∠1. Но ∠5 и ∠1 накрест лежащие. Их равенство ранее доказанному1-ому признаку параллельности означает, a||b.
Третий признак звучит так:

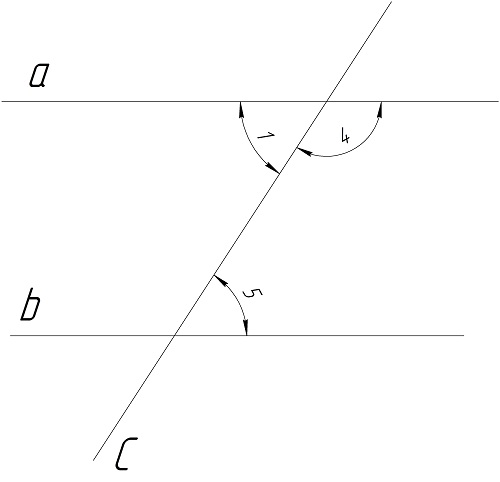
Пусть ∠5+∠4=180° (1). Так как ∠4 и ∠1 являются смежными, то для них можно записать равенство: ∠4+∠1=180°. Отсюда можно получить значение угла 4: ∠4=180°-∠1. Подставляя это уравнение в выражение (1), получаем:
∠5+(180°-∠1)=180. Раскрывая скобки и перенося слагаемые в правую часть, можно получить равенство ∠5=∠1. Но эти углы являются накрест лежащими, а потому их равенство означает, что a||b.


























