Что такое координаты вектора — какие операции можно производить
Три попарно перпендикулярные прямые с определенными направлениями и единицей измерения в геометрии составляют систему координат в пространстве. Точка, в которой пересекаются данные прямые, представляет собой начало координат.
Оси координат:
- \(Ox\) — ось абсцисс.
- \(Oy\) — ось ординат.
- \(Oz\) — ось аппликат.
Через две прямые, которые пересекаются, можно построить плоскость. Таким образом, образуются три координатные плоскости в виде:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
- \((Oxy)\);
- \((Oyz)\);
- \((Oxz)\).
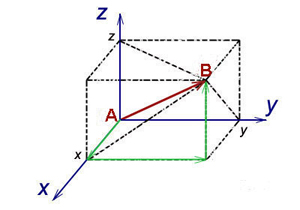
Определить положение точки \(А\) в пространстве можно с помощью трех координат \(x, y\) и \(z\).
Координата x является понятием абсциссы точки \(A\), координата y — определяет ординату точки \(A\), координата \(z\) — аппликату точки \(A\).
Запись имеет следующий вид:
\(A(x;y;z)\).
Варианты расположения точки:
- в том случае, когда точка расположена на оси \(Ox\), ее координаты — \(X(x;0;0)\);
- при нахождении точки на оси \(Oy\) она характеризуется координатами \(Y(0;y;0)\);
- если точка принадлежит оси \(Oz\), ее координаты — \(Z(0;0;z)\);
- точка, лежащая в плоскости \(Oxy\), обладает координатами \(A1(x;y;0)\);
- в том случае, когда расположение точки совпадает с плоскостью \(Oyz,\) она обладает координатами \(A2(0;y;z)\);
- если точка расположена в плоскости \(Oxz\), то данная точка имеет координаты \( A3(x;0;z)\).
Допустим, что в системе координат существуют некие единичные векторы \(\overrightarrow { i }\), \(\overrightarrow { j }\) и \(\overrightarrow { k }\), которые были отложены от начала координат. В этом случае допустимо определить прямоугольный базис. Какой-либо вектор раскладывается на единичные вектора и записывается в виде:
\(\overrightarrow {OA}=x⋅\overrightarrow { i }+y⋅\overrightarrow { j }+z⋅\overrightarrow { k }\)
Коэффициенты \(x\), \(y\) и \( z\) могут иметь одно единственное значение и являются координатами вектора.
Определение
В прямоугольной системе координат \(Х0у\) проекции х и у вектора \(\overrightarrow {OA}\) на оси абсцисс и ординат называют координатами вектора. То есть координаты вектора являются числами, описывающими положение вектора относительно координатной плоскости.
Координатами вектора, начало которого совпадает с точкой \(A(x1; y1)\), а конец — соответствует точке \(B(x2; y2)\), называют числа:
\(a1 = x2 — x1\);
\(a2 = y2 — y1\).
Координаты вектора записывают в таком виде:
\(\overrightarrow {OA}{x;y;z}\).
Правила записи с помощью координат:
Координаты суммы векторов при наличии известных координат векторов:
Координаты разности векторов при заданных координатах векторов:
Координаты произведения вектора на число при наличии определенных координатах вектора:
Длина, которой обладает вектор:
Координаты вектора при заданных координатах, которыми характеризуются начальная и конечная точки вектора:
Расстояние по модулю, на которое удалены две точки с заданными координатами:
Координаты серединной точки отрезка, когда заданы координаты начальной и конечной точек отрезка:
Координаты вектора обладают следующими свойствами:
- Какие-либо равные векторы в единой системе координат обладают идентичными координатами.
- Координаты коллинеарных векторов пропорциональны в том случае, когда ни один из векторов не обладает нулевым значением.
- Квадрат длины какого-либо вектора определяется как сумма квадратов его координат.
- В процессе умножения вектора на действительное число каждая его координата умножается на это число.
- Когда требуется сложить вектора, следует определить сумму соответствующих координат данных векторов.
- Скалярное произведение пары векторов соответствует сумме произведений их соответствующих координат.
Направляющие косинусы
Определение
Направляющими косинусами вектора
называются косинусы углов, образованных вектором с
положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для
единичного вектора направляющие косинусы
равны его координатам.
Если в пространстве задан вектор $\overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right)$, то
его направляющие косинусы вычисляются по формулам:
$\cos \alpha=\frac{a_{x}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, \cos \beta=\frac{a_{y}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}, \cos \gamma=\frac{a_{z}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$
Здесь $\alpha$, $\beta$ и
$\gamma$ — углы, которые составляет вектор с положительными
направлениями осей $O x$, $O y$ и
$O z$ соответственно.
На оси абсцисс и ординат называются координатами
вектора
.
Координаты вектора общепринято указывать в виде (х, у)
, а сам вектор как: =(х, у).
И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Что такое искусственный интеллект
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Виды векторов[править | править код]
Иногда вместо того, чтобы рассматривать в качестве векторов множество всех направленных отрезков (рассматривая как различные все направленные отрезки, начала и концы которых не совпадают), берут только некоторую модификацию этого множества (фактормножество), то есть, некоторые направленные отрезки рассматривают как равные, если они имеют одинаковое направление и длину, хотя они могут иметь разное начало (и конец), то есть направленные отрезки одинаковой длины и направления считаются представляющими один и тот же вектор; таким образом, каждому вектору оказывается соответствующим целый класс направленных отрезков, одинаковых по длине и направлению, но различающихся началом (и концом).
Так, говорят о «свободных», «скользящих» и «фиксированных» векторах. Эти виды отличаются понятием равенства двух векторов.
- Говоря о свободных векторах, отождествляют любые векторы, имеющие одинаковое направление и длину;
- говоря о скользящих векторах — добавляют, что начала равных скользящих векторов должны совпадать или лежать на одной прямой, на которой лежат изображающие эти векторы направленные отрезки (так что один может быть совмещен с другим перемещением в направлении, им же самим задаваемом);
- говоря о фиксированных векторах — говорят, что равными считаются только векторы, у которых совпадают и направления, и начала (то есть в этом случае факторизации нет: нет двух фиксированных векторов с различными началами, которые считались бы равными).
Формально:
Говорят, что свободные векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны, если найдутся точки E{\displaystyle E} и F{\displaystyle F} такие, что четырёхугольники ABFE{\displaystyle ABFE} и CDFE{\displaystyle CDFE} — параллелограммы.
Говорят, что скользящие векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны, если
- точки A,B,C,D{\displaystyle A,B,C,D} располагаются на одной прямой,
- векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны между собой как свободные векторы.
Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила, действующая на твердое тело. Перенос начала вектора силы вдоль прямой, на которой он лежит, не меняет момента силы относительно любой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (даже почти всегда вызовет): поэтому при вычислении момента нельзя рассматривать силу как свободный вектор, то есть, нельзя её считать приложенной к произвольной точке твердого тела.
Говорят, что фиксированные векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны, если попарно совпадают точки A{\displaystyle A} и C{\displaystyle C}, B{\displaystyle B} и D{\displaystyle D}.
Вектором в одном случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Все операции над векторами (сложение, умножение на число, скалярное и векторное произведения, вычисление модуля или длины, угла между векторами и т. д.) в принципе определены одинаково для всех типов векторов, различие в типах сводится в этом отношении только к тому, что для скользящих и фиксированных наложено ограничение на возможность осуществления операций между двумя векторами, имеющими разное начало (так, для двух фиксированных векторов запрещено — или лишено смысла — сложение, если их начала отличаются; однако для всех случаев, когда эта операция разрешена — или имеет смысл — она такова же, как для свободных векторов). Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса и т. п.), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).
Элементы вектора
В основном вектор имеет три элемента: направление, смысл и модуль.
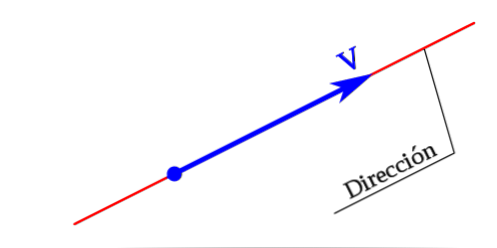
Вектор — это объект, который имеет величину и направление. Примеры векторов включают смещение, скорость, ускорение и силу.
Чтобы описать одну из этих векторных величин, необходимо найти величину и направление.
Например, если скорость объекта составляет 25 метров в секунду, то описание скорости объекта является неполным, поскольку объект может двигаться со скоростью 25 метров в секунду к югу или 25 метров в секунду к северу, или 25 метров в секунду к юго-востоку.
Чтобы полностью описать скорость объекта, должны быть определены оба: и величина 25 метров в секунду, и направление, например, на юг.
Чтобы такие описания векторных величин были полезными, важно, чтобы каждый согласился с тем, как описывается направление объекта.. Большинство людей привыкли к мысли, что восточное направление указано на карте, если вы посмотрите направо
Но это простая договоренность, которую картографы использовали годами, чтобы каждый мог договориться
Большинство людей привыкли к мысли, что восточное направление указано на карте, если вы посмотрите направо. Но это простая договоренность, которую картографы использовали годами, чтобы каждый мог договориться.
Так, каково направление векторной величины, которая не идет на север или восток, если не где-то между севером и востоком? Для этих случаев важно, чтобы было какое-то соглашение для описания направления указанного вектора.. Эта конвенция называется CCW
Используя это соглашение, мы можем описать направление любого вектора с точки зрения его угла поворота влево
Эта конвенция называется CCW. Используя это соглашение, мы можем описать направление любого вектора с точки зрения его угла поворота влево.
При использовании этого соглашения направление на север будет составлять 90 °, поскольку, если вектор указывает на восток, его необходимо повернуть на 90 ° влево, чтобы достичь точки севера..
Кроме того, направление на запад было бы расположено на 180 °, поскольку вектор, указывающий на запад, должен был бы поворачиваться на 180 ° влево, чтобы указывать на западную точку..
Другими словами, направление вектора будет представлено линией, содержащейся в векторе, или любой линией, параллельной ему.,
Она определяется углом, образованного между вектором и любой другой опорной линией. Таким образом, направление линии, которая находится в векторе или некоторой линии, параллельной ему, является направлением вектора.
чувство
Смысл вектора относится к элементу, который описывает, как точка A подходит к концу B:
Смысл вектора определяется порядком двух точек на линии, параллельной вектору, в отличие от направления вектора, которое определяется отношением между вектором и любой базовой линией и / или плоскостью.
Направление и смысл определяют направление вектора. Ориентация говорит, под каким углом находится вектор, а смысл говорит, куда он указывает.
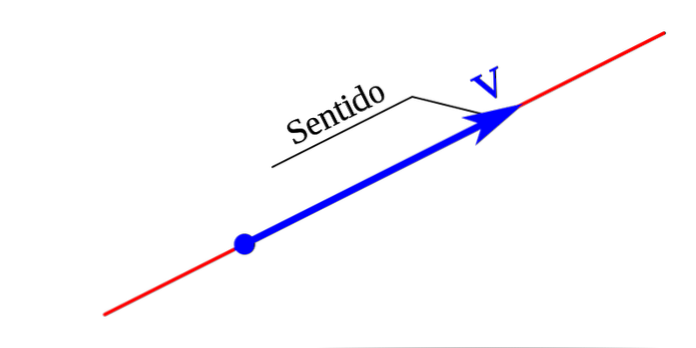
Направление вектора устанавливает только угол, который вектор составляет с его горизонтальной осью, но это может создать неоднозначность, поскольку стрелка может указывать в двух противоположных направлениях и при этом оставаться под тем же углом..
Смысл проясняет эту двусмысленность и указывает, куда указывает стрелка или куда идет вектор.
Почему-то смысл подсказывает нам порядок чтения вектора. Указывает, где вектор начинается и заканчивается.
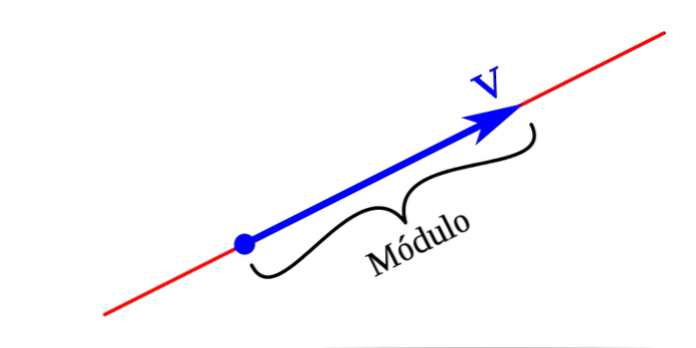
Модуль или амплитуду вектора можно определить как длину сегмента AB. Модуль может быть представлен длиной, которая пропорциональна значению вектора. Модуль вектора всегда будет равен нулю или в других случаях некоторому положительному числу.
В математике вектор будет определяться его евклидовым расстоянием (модулем), направлением и смыслом.
Евклидово расстояние или евклидово расстояние — это «обычное» расстояние по прямой линии между двумя точками, расположенными в евклидовом пространстве. С этим расстоянием евклидово пространство становится метрическим пространством.
Евклидово расстояние между двумя точками, например, P и Q, является расстоянием между отрезком, соединяющим их:
Положение точки в евклидовом пространстве n является вектором. Таким образом, P и Q являются векторами, начиная с начала пространства и их точек, указывающих две точки.
Евклидова норма, величина или евклидово расстояние вектора измеряют длину указанного вектора.
ссылки
- Вектор направления Получено с сайта physclassroom.com..
- В чем смысл вектора? Получено с сайта физики.stackexchange.com..
- В чем разница между направлением, смыслом и ориентацией? Получено с сайта math.stackexchange.com.
- Евклидово расстояние. Получено с wikipedia.org.
Операции над отрезками
Любые геометрические свойства векторов можно перенести на систему координат — как двоичную, так и троичную. Впоследствии приобретаются алгебраические характеристики, что упрощает способы вычисления. Можно привести в пример несколько классических операций:
- Модуль. Это то же самое, что и длина.
- Сложение. Высчитывается путем суммирования координатных слагаемых.
- Модуль суммы. Вычисляется посредством теоремы косинусов.
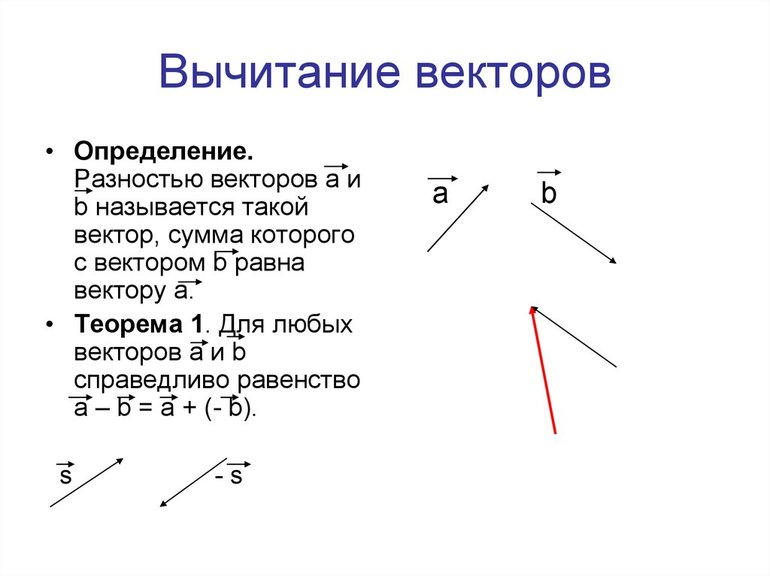
- Вычитание. Высчитывается путем получения разности соответствующих координатных показателей.
- Модуль разности. Здесь также задействуется теорема косинусов, однако перед угловой величиной ставится знак минус.
- Умножение на число. Если показатель имеет положительное значение, то вектор будет сонаправленным, больше в указанное количество раз. Если отрицательное, то противоположно ориентированным.
- Скалярное произведение. Вычисляется через геометрические характеристики. В формуле присутствует значение косинуса — рассматривается угол, который образуется, если отрезки наложить друг на друга, но направление оставить прежним.
- Векторное произведение. Для вычисления задействуется трехмерное пространство. Чтобы получить результат, необходимо чертить перпендикулярно расположенный вектор (относительно двух других).
Сложнее всего выполняются операции по произведению. Здесь задействуются алгебраические и геометрические свойства. Удобнее видеть чертеж, ориентироваться по нему. Когда отрезки наложены друг на друга либо имеется перпендикуляр (в трехмерном пространстве), выводить математические значения намного проще.
https://youtube.com/watch?v=EA8aSyZ1tow
Понятие вектора
Тот факт, что вектор — это направленный отрезок, будет проще понять, остановившись
на различиях между скалярными и векторными величинами.
В приведенной ниже таблице «Не векторы» — это скалярные величины или просто скаляры,
а «Векторы» — векторные величины.
| Не векторы | Векторы |
| Масса | Сила тяжести |
| Длина | Путь |
| Время | Ускорение |
| Плотность | Давление |
| Температура | Скорость |
| Объем | |
| Площадь | |
| Модуль вектора |
Не векторы (скаляры) не имеют направления, а векторы имеют направление.
Вектор обязательно идёт от некоторой точки A по прямой к некоторой точке
B. Числовое значение вектора — длина, а физическое и геометрическое — направление. Из этого и выводится первое, самое простое определение вектора. Итак, вектор —
это направленный отрезок, идущий от точки A к точке B. Обозначается он так:
.
А чтобы приступить к различным операциям с векторами, нам нужно познакомиться
с ещё одним определением вектора.
Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной
точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем
просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях,
чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает
вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку,
проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении,
указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец,
окажетесь в конечной точке.

Все остальные термины — это уточнения представленного выше объяснения, необходимые для
различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим
более строгим определениям, останавливаясь на типичных задачах на векторы.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве,
скорость и ускорение этой точки, а также действующая на неё сила.
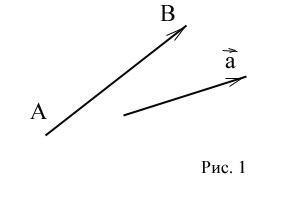
Геометрический вектор представлен
в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало
и конец.
Если A — начало вектора, а B — его конец, то вектор обозначается
символом или одной строчной буквой . На рисунке
конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора
называется длина порождающего его отрезка
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений)
путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением.
Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку
пространства. В этом случае вектор называется свободным. В курсе высшей математики
векторы изучаются в разделе аналитической геометрии, где рассматриваются свободные векторы. Итак, если свободный вектор —
это вектор, начало которого может быть в любой точке пространства, то все векторы одинакового направления
и длины считаются равными.
9 Правило параллелепипеда
Параллелепипед
— это объемная фигура, противоположные грани которой состоят из двух
равных параллелограммов, лежащих в параллельных плоскостях.
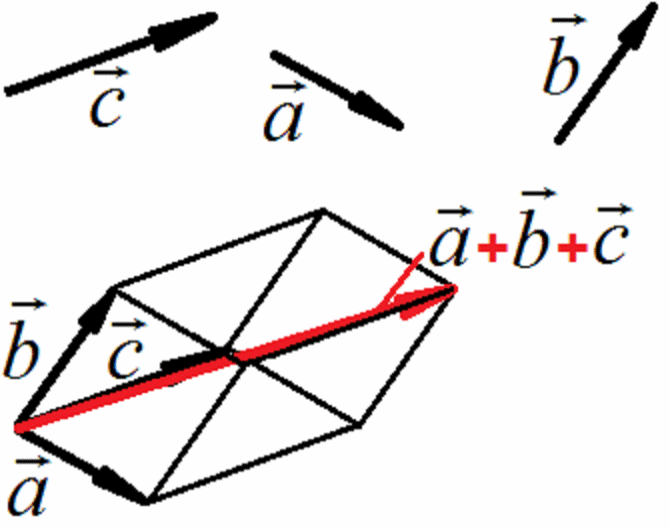
Правило
параллелепипеда позволяет складывать три некомпланарных вектора,
которые откладываются из одной точки и строится параллелепипед так,
чтобы суммируемые векторы образовывали его ребра, а остальные ребра
параллелепипеда были соответственно параллельны и равны длинам ребер,
образованных суммируемыми векторами. Диагональ параллелепипеда
образует вектор, являющийся суммой заданных трех векторов, который
начинается из точки начала складываемых векторов.
Признак коллинеарности векторов
Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что

Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:
x1 = k * x2
y1 = k * y2
Если числа х2 и у2 не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:
Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.

Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.
Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты {8; 5}, а у вектора b они равны {24; 15}. Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:
24:8 = 3
Получили число 3. Далее поделим и координаты у:
15:5 = 3
Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:
В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:
Естественно, снова получилось одинаковое число.
Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты {0; у1}, причем у1≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты {x2; у2} составят:
Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у2 и у1 могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие
y2 = ky1
Например, есть вектор {0; 5}. Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,
![]()
Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору {0; 5}. В частности, ему не будут коллинеарны вектора:
![]()
Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.

Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.
Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:
Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:

Числа различны, поэтому вектора НЕ коллинеарны.
В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.
е) {0; 5} и {0; 12}
У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.
ж) {0; 3} и {2; 6}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
з) {9; 0} и {4; 0}
У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.
и) {0; 3} и {12; 0}
Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.
к) {0; 0} и {5; 8}
Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.
Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.
Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.


























