Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π | |
| cos x |
1 |
√3/2 (0,8660) |
√2/2 (0,7071) |
1/2 (0,5) |
-1/2 (-0,5) |
-√2/2 (-0,7071) |
-√3/2 (-0,8660) |
-1 |
-√3/2 (-0,8660) |
-√2/2 (-0,7071) |
-1/2 (-0,5) |
1/2 (0,5) |
√2/2 (0,7071) |
√3/2 (0,8660) |
1 |
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.
1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус.
И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются»
: синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами».
Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Синусы — «смешиваются»
:
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами
. А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Формулы произведения синусов, косинусов и синуса на косинус
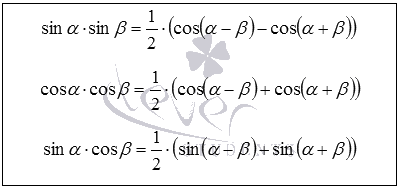
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Башмаков М. И.
Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра
и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
Гусев В. А., Мордкович А. Г.
Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Таблица значений тригонометрических функций
Примечание
. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».
См. также
полезные материалы:
Для определения значения тригонометрической функции
, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60
градусов, синус 60
градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Синус пи, косинус пи, тангенс пи и других углов в радианах
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах
. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.
Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180
.
Примеры
:
1. Синус пи
.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.
2. Косинус пи
.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.
3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.
|
значение угла α (градусов) |
значение угла α (через число пи) |
sin (синус)
|
cos (косинус)
|
tg (тангенс)
|
ctg (котангенс)
|
sec (секанс)
|
cosec (косеканс)
|
| 1 | — | 1 | — | ||||
|
15 |
π/12 |
2 — √3 | 2 + √3 | ||||
|
30 |
π/6 |
1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
|
45 |
π/4 |
√2/2 | √2/2 | 1 | 1 | √2 | √2 |
|
60 |
π/3 |
√3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
|
75 |
5π/12 |
2 + √3 | 2 — √3 | ||||
|
90 |
π/2 |
1 | — | — | 1 | ||
|
105 |
7π/12 |
— | — 2 — √3 | √3 — 2 | |||
|
120 |
2π/3 |
√3/2 | -1/2 | -√3 | -√3/3 | ||
|
135 |
3π/4 |
√2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
|
150 |
5π/6 |
1/2 | -√3/2 | -√3/3 | -√3 | ||
|
180 |
π |
-1 | — | -1 | — | ||
|
210 |
7π/6 |
-1/2 | -√3/2 | √3/3 | √3 | ||
|
240 |
4π/3 |
-√3/2 | -1/2 | √3 | √3/3 | ||
|
270 |
3π/2 |
-1 | — | — | -1 | ||
|
360 |
2π |
1 | — | 1 | — |
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
Определение знака
Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.
Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.
Дополнительные сведения
Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).
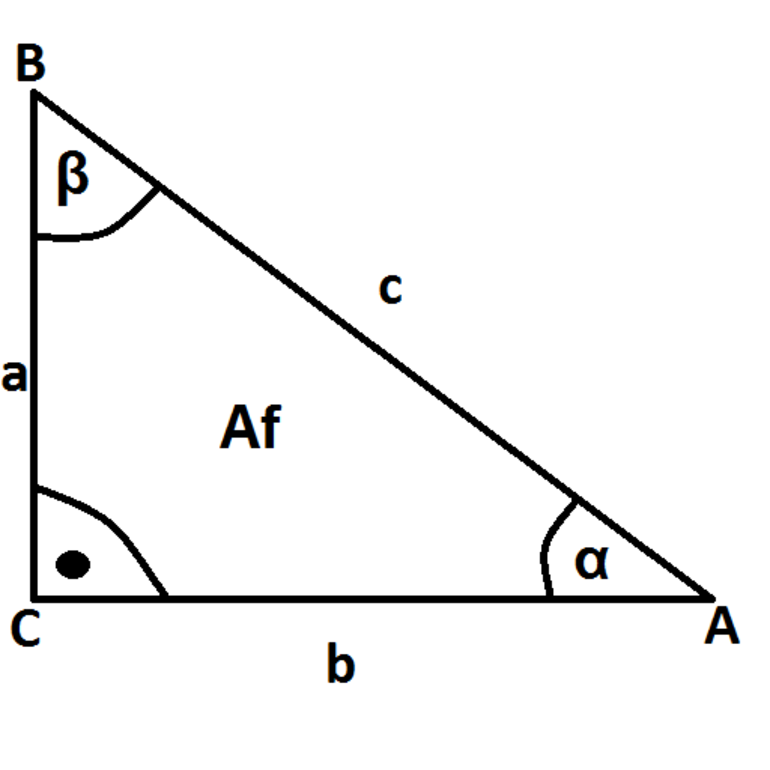
Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180
Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).
Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).
Построение окружности
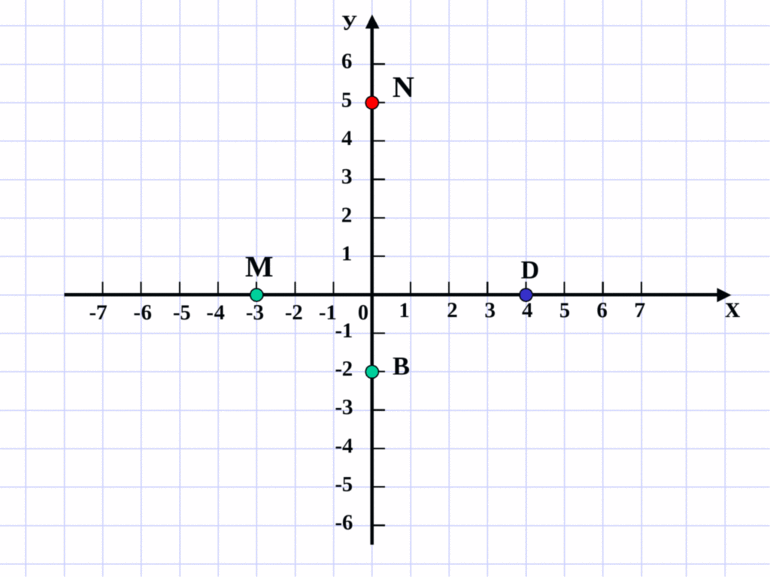
Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».
Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
- Координаты заключаются в круглые скобки и разделяются «;».
- На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:
- Значения по x и y больше 0 соответствуют первой четверти (I).
- II: x<0 и y>0.
- III: x<0 и y<0.
- IV: x>0 и y<0.
Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:
- 0 и 2ПИ (0 и 360 градусов) — (1;0).
- ПИ/2 (90) — (0;1).
- 3ПИ/2 (270) — (1;0).
Использование готового инструмента
Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).
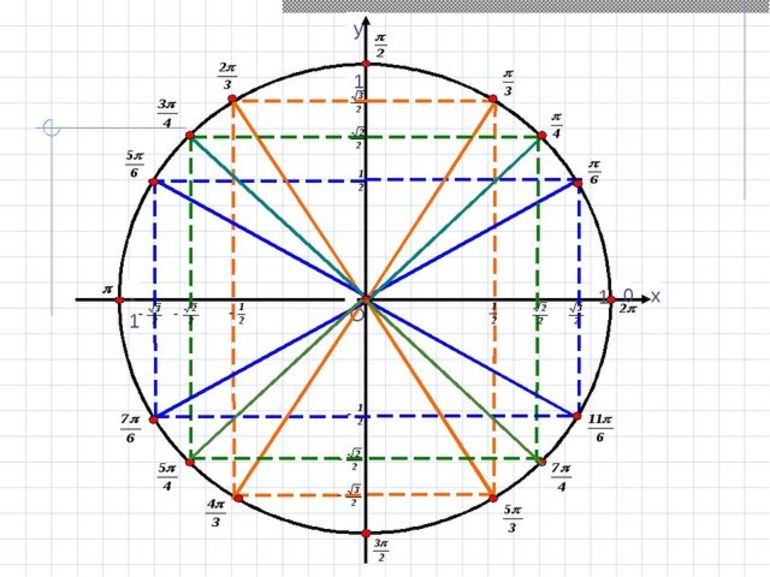
Рисунок 1. Пример тригонометрического круга.
Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:
- cos(-a) = cos(a).
- sin(-a) = -sin(a).
- tg(-a) = -tg(a).
- ctg(-a) = -ctg(a).
С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:
- Определить четверть, в которой находится угол: 240 = 4ПИ/3 соответствует III четверти.
- В III четверти величина функции принимает только отрицательные значения. Значит, перед ней следует поставить знак «минус».
- Вычислить: cos(4ПИ/3) = — 1/2.
Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Определение и свойства функции
Функция — это математический объект, который сопоставляет каждому элементу из одного множества (называемого областью определения функции) элемент из другого множества (называемого областью значений функции).
Функцию можно задать различными способами, например, формулой, графиком или таблицей значений.
Свойства функции:
-
Функция однозначно определена: каждому элементу из области определения соответствует только один элемент из области значений.
-
Функция может быть задана явно или неявно.
-
Явное задание функции — это когда функция задается формулой, например, f(x) = x^2.
-
Неявное задание функции — это когда функция задается условием или отношением, например, x^2 + y^2 = 1 задает неявную функцию y(x).
-
-
Функция может быть определена на частичной или полной области определения.
-
Частичная область определения — это область значений, на которой функция определена только для некоторых элементов из области определения.
-
Полная область определения — это область значений, на которой функция определена для всех элементов из области определения.
-
-
Функция может быть четной или нечетной.
-
Четная функция — это функция, у которой значение в точке x равно значению в точке -x, т.е. f(x) = f(-x) для всех x из области определения функции.
-
Нечетная функция — это функция, у которой значение в точке x равно значению в точке -x с измененным знаком, т.е. f(x) = -f(-x) для всех x из области определения функции.
-
-
Функция может быть периодической или непериодической.
-
Периодическая функция — это функция, у которой значение в точке x равно значению в точке x + T, где T — некоторая константа.
-
Непериодическая функция — это функция, у которой нет периода.
-
Это основные свойства функции, которые помогают понять ее характеристики и использовать ее для решения различных задач в математике и других науках.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 9. Тригонометрическая окружность, табличные значения
На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии. М
ы увидим, что она — основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.
Мы поймем, как «работает» окружность — а значит, поймём тригонометрию в целом.
ЕГЭ 13б. Тригонометрическая окружность
Тригонометрическая окружность — это очень простой и эффективный инструмент для решения любой тригонометрической задачи. На этом уроке вы узнаете как пользоваться тригонометрической окружностью для решения пункта «б» из задачи №13 профильного ЕГЭ.
Пункт “б” задачи №13 ЕГЭ 2020 В 2020 году на ЕГЭ в пункте «б» необходимо было указать корни тригонометрического уравнения принадлежащие отрезку.
Вообще-то решать пункт “б” можно двумя способами: — отметить корни уравнения на единичной окружности (способ разобранный в этом видео); — через двойное неравенство.
И вы должны знать, что второй способ чуть дольше, чем первый, но зато вы сможете проще описать все ваши рассуждения и вам будет сложнее ошибиться.
И еще один плюс второго способа — его проще оформить, так, чтобы к вам не придрались на ЕГЭ.
Мы считаем второй способ (через двойное неравенство) более предпочтительным на ЕГЭ по математике, но теме не менее для глубокого понимания темы (что может выручить на ЕГЭ) необходимо разобраться и с первым способом
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента x 0
и отсчитать от оси Ox
угол x
0, то этому углу на единичной окружности соответствует некоторая точка A
(рис. 1)а ее проекцией на ось Ох
будет точка М
.Длина отрезка ОМ
равна абсолютной величине абсциссы точки A
. Данному значению аргумента x 0
сопоставлено значение функции y
= cos x
0 как абсциссы точки А
.Соответственно точка В
(x
0 ; у
0)принадлежит графику функции у
= cos х
(рис. 2).Если точка А
находится правее оси Оу
,токосинус будет положителен, если же левее – отрицателен. Но в любом случае точка А
не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:
–1 = cos x
= 1.
Дополнительный поворот на любой угол, кратный 2p
, возвращает точку A
на то же место. Поэтому функция у =
cos x
p
:
cos (x
+ 2p
) = cos x.
Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x
и –x
,найти на окружности соответствующие точки A x
и А -x
.Как видно на рис. 3их проекцией на ось Ох
является одна и та же точка М
.Поэтому
cos (–x
) = cos (x
),
т.е. косинус – четная функция, f
(–x
) = f
(x
).
Значит, можно исследовать свойства функции y
= cos х
на отрезке ,
а затем учесть ее четность и периодичность.
При х
= 0 точка А
лежит на оси Ох
,ее абсцисса равна 1, а потому cos 0 = 1. С увеличением х
точка А
передвигается по окружности вверх и влево, ее проекция, естественно, только влево, и при х = p
/2 косинус становится равен 0. Точка A
в этот момент поднимается на максимальную высоту, а затем продолжает двигаться влево, но уже снижаясь. Ее абсцисса все убывает, пока не достигнет наименьшего значения, равного –1 при х
= p
. Таким образом, на отрезке функция у
= cos х
монотонно убывает от 1 до –1 (рис. 4, 5).
Из четности косинуса следует, что на отрезке [–p
, 0] функция монотонно возрастает от –1 до 1, принимая нулевое значение при х =
–p
/2. Если взять несколько периодов, получится волнообразная кривая (рис. 6).
Итак, функция y
= cos x
принимает нулевые значения в точках х
= p
/2 + kp
,где k –
любое целое число. Максимумы, равные 1, достигаются в точках х
= 2kp
, т.е. с шагом 2p
, а минимумы, равные –1, в точках х
= p
+ 2kp
.
Синус, косинус, тангенс и котангенс: основные формулы
Формулы приведения
По этим формулам значение тригонометрической функции аргумента a, где p/2 < a < 2p, можно привести к значению функции аргумента a, где 0 < a < p/2, как той же, так и дополнительной к ней.
| Аргумент b
Функция |
– a | + a | p – a | p + a | + a | + a | 2p – a |
| sin b | cos a | cos a | sin a | –sin a | –cos a | –cos a | –sin a |
| cos b | sin a | –sin a | –cos a | –cos a | –sin a | sin a | cos a |
Поэтому в таблицах тригонометрических функций даются значения только для острых углов, причем достаточно ограничиться, например, синусом и тангенсом. В таблице даны только наиболее употребительные формулы для синуса и косинуса. Из них легко получить формулы для тангенса и котангенса. При приведении функции от аргумента вида kp/2 ± a, где k – целое число, к функции от аргумента a:
- название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
- знак в правой части совпадает со знаком приводимой функции в точке kp/2 ± a, если угол a острый.
Например, при приведении ctg (a – p/2) убеждаемся, что a – p/2 при 0 < a < p/2 лежит в четвертом квадранте, где котангенс отрицателен, и, по правилу 1, меняем название функции: ctg (a – p/2) = –tg a.
sin (ab) = sin a cos b cos a sin b;
cos (ab) = cos a cos b sin a sin b
Формулы кратных углов
Эти формулы выводятся прямо из формул сложения:
sin 2a = 2 sin a cos a;
cos 2a = cos2a – sin2a = 2 cos2a – 1 = 1 – 2 sin2 a;
sin 3a = 3 sin a – 4 sin3a;
cos 3a = 4 cos3a – 3 cos a;
Формулу для cos 3a использовал Франсуа Виет при решении кубического уравнения. Он же впервые нашел выражения для cos na и sin na, которые позже были получены более простым путем из формулы Муавра.
Если в формулах двойного аргумента заменить a на a/2, их можно преобразовать в формулы половинных углов.
Формулы универсальной подстановки
Используя эти формулы, выражение, включающее разные тригонометрические функции от одного и того же аргумента, можно переписать как рациональное выражение от одной функции tg (a/2), это бывает полезно при решении некоторых уравнений.
Формулы преобразования сумм в произведения и произведений в суммы.
До появления компьютеров эти формулы использовались для упрощения вычислений. Расчеты производились с помощью логарифмических таблиц, а позже – логарифмической линейки, т.к. логарифмы лучше всего приспособлены для умножения чисел, поэтому все исходные выражения приводили к виду, удобному для логарифмирования, т.е. к произведениям, например:
2 sina sin b = cos (a – b) – cos (a + b);
2 cos a cos b = cos (a – b) + cos (a + b);
2 sin a cos b= sin (a – b) + sin (a + b).
Формулы для функций тангенса и котангенса можно получить из вышеприведенных.
Формулы понижения степени
Из формул кратного аргумента выводятся формулы:
| sin2a = (1 – cos 2a)/2; | cos2a = (1 + cos 2a)/2; |
| sin3a = (3 sin a – sin 3a)/4; | cos3a = (3 cosa + cos 3a)/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
| (tg x)` = ; | (ctg x)` = – ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
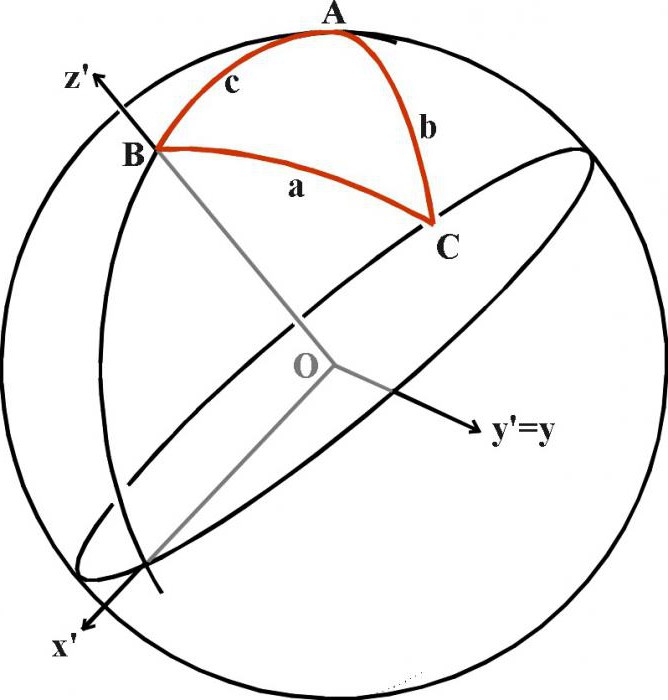
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой
Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях
Формулы двойного угла
Формулы двойного угла для синуса, косинуса, тангенса и котангенса дают возможность выразить двойной угол \(2\alpha\) через \(\alpha\). Формулы для синуса и косинуса очень часто встречаются на ЕГЭ. Их обязательно нужно знать. Все они легко выводятся из формул синуса и косинуса суммы (формулы №5 и №6) :
$$\cos(2\alpha)=\cos(\alpha+\alpha)=\cos(\alpha)*\cos(\alpha)-\sin(\alpha)*\sin(\alpha)=\cos^2(\alpha)-\sin^2(\alpha);$$
Воспользовавшись основным тригонометрическим тождеством можно преобразовать эту формулу:
$$\cos(2\alpha)=\cos^2(\alpha)-\sin^2(\alpha)=1-\sin^2(\alpha)-\sin^2(\alpha)=1-2\sin^2(\alpha);$$
$$\cos(2\alpha)=\cos^2(\alpha)-\sin^2(\alpha)=\cos^2(\alpha)-(1-\cos^2(\alpha))=2\cos^2(\alpha)-1;$$
Синус двойного угла выводится аналогичным образом только с использованием формулы синуса суммы:
$$\sin(2\alpha)=\sin(\alpha)*\cos(\alpha)+\sin(\alpha)*\cos(\alpha)=2\sin(\alpha)\cos(\alpha);$$
Для вывода формул двойного угла для тангенса нам понадобится представить тангенс в виде отношения синуса к косинуса по определению и только что выведенные формулы синуса и косинуса двойного угла:
$$tg(2\alpha)=\frac{\sin(2\alpha)}{\cos(2\alpha)}=\frac{2\sin(\alpha)\cos(\alpha)}{\cos^2(\alpha)-\sin^2(\alpha)}=\frac{\frac{2\sin(\alpha)\cos(\alpha)}{\cos^2(\alpha)}}{\frac{\cos^2(\alpha)-\sin^2(\alpha)}{\cos^2(\alpha)}}=\frac{\frac{2\sin(\alpha)}{\cos(\alpha)}}{1-\frac{\sin^2(\alpha)}{\cos^2(\alpha)}}=\frac{2tg(\alpha)}{1-tg^2(\alpha)};$$
Котангенс двойного угла выводится абсолютно также:
$$сtg(2\alpha)=\frac{\cos(2\alpha)}{\sin(2\alpha)}=\frac{\cos^2(\alpha)-\sin^2(\alpha)}{2\sin(\alpha)\cos(\alpha)}=\frac{\frac{\cos^2(\alpha)-\sin^2(\alpha)}{\sin^2(\alpha)}}{\frac{2\sin(\alpha)\cos(\alpha)}{\sin^2(\alpha)}}=\frac{\frac{\cos^2(\alpha)}{\sin^2(\alpha)}-1}{\frac{2\cos(\alpha)}{\sin(\alpha)}}=\frac{ctg^2(\alpha)-1}{2ctg(\alpha)};$$
В первой части на ЕГЭ попадаются номера на преобразование тригонометрических выражений, где часто содержится двойной угол:
Пример 6
Найти значение \(24\cos(2\alpha)=?\), если \(\sin(\alpha)=-0,2.\)
Воспользуемся формулой косинуса двойного угла:
$$\cos(2\alpha)=1-2\sin^2(\alpha);$$
$$24\cos(2\alpha)=24(1-2\sin^2(\alpha))=24-48\sin^2(\alpha)=24-48*(-0,2)^2=24-48*0,04=22,08.$$
Пример 7
Найти значение \(\frac{10\sin(6\alpha)}{3\cos(3\alpha)}=?\), если \(\sin(3\alpha)=0,6.\)
Используем синус двойного угла, для этого представим \(6\alpha=2*(3\alpha)\):
$$\sin(6\alpha)=\sin(2*(3\alpha))=2\sin(3\alpha)\cos(3\alpha);$$
$$\frac{10\sin(6\alpha)}{3\cos(3\alpha)}=\frac{10*2\sin(3\alpha)\cos(3\alpha)}{3\cos(3\alpha)}=\frac{20\sin(3\alpha)}{3}=\frac{20*0,6}{3}=\frac{12}{3}=4.$$
Пример 8
Найти значение выражения \(\frac{12\sin(11^o)\cos(11^o)}{\sin(22^o)}=?\)
Замечаем, что \(22^o=2*11^o\) и воспользуемся синусом двойного угла:
$$\frac{12\sin(11^o)\cos(11^o)}{\sin(22^o)}=\frac{12\sin(11^o)\cos(11^o)}{2\sin(11^o)\cos(11^o)}=\frac{12}{2}=6.$$
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.




![Тригонометрические выражения и тригонометрические формулы [wiki.eduvdom.com]](http://podomu.info/wp-content/uploads/5/4/2/5429b3663f6492b1b736ed33d244f040.jpeg)
























