Формулы понижения степени
Как считать выражения, в которых тригонометрическая функция стоит в квадрате? Просто возвести табличное значение в квадрат? А если в аргументе не табличное значение, но необходимо воспользоваться аркфункцией (еще немного терпения, мы обязательно разберемся, что же это за зверь такой)? Спойлер: аркфункцией нельзя пользоваться, если тригонометрическая функция стоит в квадрате.
Как тогда преобразовывать такие выражения? Снова воспользоваться формулами:
\(sin^2x=\frac{1-cos(2x)}{2}\)\(cos^2x=\frac{1+cos(2x)}{2}\)\(tg^2x=\frac{1-cos(2x)}{1+cos(2x)}\)\(ctg^2x=\frac{1+cos(2x)}{1-cos(2x)}\)
Первые две формулы легко вывести из косинуса двойного угла. Например:
\(cos(2x)=1-2sin^2x\)\(2sin^2x=1-cos(2x)\)\(sin^2x=\frac{1-cos(2x)}{2}\)
| Лайфхак: что делать, если забыл нужную формулу? Особая прелесть формул в тригонометрии в том, что они неразрывно связаны друг с другом. И если случилось так, что вы забыли одну из формул, ее легко можно вывести из другой! Например, как вывести формулу понижения степени из формулы косинуса двойного угла мы разобрали только что. |
Теперь попробуем составить алгебраическое выражение с самими тригонометрическими функциями. Для усложнения задачи у них будут разные аргументы.
Основная теорема
Эта теорема позволяет решать огромное количество задач — от самых простых до весьма нетривиальных. Начнём с простых.
Из всех чертежей видно, что при пересечении двух прямых обычно возникает два острых угла и два тупых. Причём острый и тупой угол всегда будут смежными.
Если предположить, что острый угол равен $\color{red}{x}$ градусов, то тупой равен $180-\color{red}{x}$ градусов.
Единственный случай, когда все вертикальные углы равны — это когда прямые перпендикулярны, т.е. пересекаются под углом 90°.
Перед тем как переходить к более сложным задачам, рассмотрим ещё одно интересное свойство вертикальных углов.
Основное тригонометрическое тождество
Эту формулу можно считать главной и самой часто используемой в тригонометрии. Она выводится при помощи определения синуса и косинуса через прямоугольный треугольник и теоремы Пифагора. Не буду еще раз описывать вывод, с ним можно познакомиться в самой первой главе по тригонометрии.
При помощи основного тригонометрического тождества очень удобно искать значение синуса, если известен косинус и наоборот. Разберем пример:
Пример 1Найдите \(3\sqrt{2}*\sin(\alpha)=?\), если \(\cos(\alpha)=\frac{1}{3}\) и \(\alpha\in(0;\frac{\pi}{2})\). (ЕГЭ)
Чтобы найти значение выражения \(3\sqrt{2}*\sin(\alpha)\), необходимо сначала найти значение синуса.
Формула, которая связывает и синус, и косинус — это основное тригонометрическое тождество:
$$\sin^2(\alpha)+\cos^2(\alpha)=1;$$
Просто подставим в нее известное значение косинуса
$$\sin^2(\alpha)+\left(\frac{1}{3}\right)^2=1;$$
$$\sin^2(\alpha)+\frac{1}{9}=1;$$
$$\sin^2(\alpha)=1-\frac{1}{9};$$
$$\sin^2(\alpha)=\frac{8}{9};$$
$$\sin(\alpha)=\pm\sqrt{\frac{8}{9}}=\pm\frac{2\sqrt{2}}{3};$$
Обратите внимание на знак \(\pm\), отрицательное значение синуса нас тоже устраивает, так как при подстановке и возведении в квадрат знак минус исчезает. В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
Какое же значение синуса нам выбрать: положительное или отрицательное?
В задании указано, что это пример из ЕГЭ первой части, значит должен быть только один ответ. Какое же значение синуса нам выбрать: положительное или отрицательное?
В этом нам поможет дополнительное условие на \(\alpha\in(0;\frac{\pi}{2})\), что соответствует первой четверти на тригонометрической окружности. Раз \(\alpha\) лежит в первой четверти, то синус должен быть положительный. Выбираем положительное значение синуса:
$$\sin(\alpha)=\frac{2\sqrt{2}}{3};$$
И подставим найденное значение в искомое выражение:
$$3\sqrt{2}*\sin(\alpha)=3\sqrt{2}*\frac{2\sqrt{2}}{3}=4.$$
Ответ: \(4.\)
Аналогично по основному тригонометрическому тождеству можно находить значение косинуса, если известен синус.
Основное тригонометрическое тождество — это ключ к решению более половины всех тригонометрических уравнений.
Полный оборот и развернутый угол
В геометрии угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной и той же точки. Углы могут иметь различные величины и виды. Один из видов углов — развернутый угол и его особый случай — полный оборот.
Развернутый угол — это угол, мера которого составляет от 180 до 360 градусов. Он получает такое название, потому что его вершина покрывает пространство, «разворачивается» на плоскости на большой угол.
Полный оборот — это особый случай развернутого угла, когда мера угла составляет 360 градусов. В этом случае угол «разворачивается» полностью и возвращается в исходную точку. Полный оборот считается самым большим углом.
Например:
- Развернутый угол может встречаться в природе, например, угол, образуемый наличием двух полных лунных дисков под углом относительно друг друга.
- Полный оборот можно увидеть на циферблате часов, где 360 градусов отображают все 12 часов.
Важно понимать, что полный оборот равен двум полным пи (2π) радианам
| Величина угла | Вид угла |
|---|---|
| Меньше 180 градусов | Острый угол |
| 180 градусов | Прямой угол |
| Между 180 и 360 градусов | Развернутый угол |
| 360 градусов | Полный оборот |
Особенности смежного угла
Смежные углы — это пара углов, которые имеют общую вершину и общую сторону между ними. Они расположены таким образом, что если поместить их один на другой, то общая вершина и общая сторона совпадут.
Основные особенности смежных углов:
- Смежные углы всегда лежат на одной прямой. Это означает, что их сумма равна 180 градусов.
- Если смежные углы равны (т.е. их меры равны), то каждый из них будет равен 90 градусам и они образуют прямой угол.
- Если смежные углы формируют две прямые линии, то их сумма будет равна 360 градусам.
- Смежные углы могут быть внутренними и внешними. Внутренние смежные углы лежат внутри сферы прямой, образующей основу. Внешние смежные углы лежат за пределами этой сферы.
- Смежные углы встречаются в различных геометрических фигурах, таких как треугольники и многоугольники. Они могут быть использованы для вычисления и нахождения неизвестных углов и сторон в этих фигурах.
Примеры бета угла в различных областях
1. Физика элементарных частиц:
Бета угол используется в физике элементарных частиц для описания слабых взаимодействий. Он определяет вероятность перехода нейтрино через слабое поле и связан с распадом нейтронов и других протонов в ядрах.
2. Геометрия:
В геометрии бета угол может использоваться для определения отклонения луча света при его прохождении через двумерный объект или преломление при переходе из одной среды в другую. Например, при изготовлении линз и при расчете показателя преломления материалов.
3. Экономика:
В экономике бета угол используется для определения степени риска или чувствительности актива к изменениям стоимости рыночного портфеля. Это показатель меры финансового риска и важен при оценке инвестиционных возможностей.
Приведенные примеры демонстрируют разнообразные области применения бета угла и его важность для понимания и решения различных задач в науке и практике
Примечания
- ↑ . УчительPRO. Дата обращения: 5 сентября 2023.
- . Авторская платформа Pandia.ru. Дата обращения: 5 сентября 2023.
- . Школьная математика. Дата обращения: 5 сентября 2023.
- ↑ . Мир математики. Дата обращения: 5 сентября 2023.
- . Онлайн учебник по русскому языку и математике | izamorfix.ru. Дата обращения: 6 сентября 2023.
- . Математический портал — образовательные онлайн сервисы по математике, физике, теории вероятности и другим предметам. Дата обращения: 6 сентября 2023.
- . Онлайн учебник по русскому языку и математике | izamorfix.ru. Дата обращения: 6 сентября 2023.
- . ООО «Микрон» | Инструмент для предприятий (18 января 2022).
- . Большая Советская энциклопедия. Дата обращения: 6 сентября 2023.
- . Azbukametalla | Энциклопедия. Дата обращения: 6 сентября 2023.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х . Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Символы вероятности и статистики
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ⋂ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ⋂ B ) = 0,5 |
| P ( A ⋃ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ⋃ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( x макс + x мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
\ и \ полностью совмещаются при наложении следовательно: \
\ и \ не совмещаются при наложении: \
Причем: \
При этом развернутые углы всегда являются равными.
Совмещение углов \ и \ происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Please enable JavaScript.
Coggle requires JavaScript to display documents.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые…
- Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой
- Виды треугольников
- По углам
Признаки равенства прямоугольных треугольников
По двум катетам
По катету и острому углу
По гипотенузе и острому углу
По гипотенузе и катету
Свойства:
Сумма острых углов прямоугольного треугольника равна 90˚.
Катет, противолежащий углу в 30˚, равен половине гипотенузы.
Теорема Пифагора квадрат гипотенузы равен сумме квадратов катетов.
Центр описанной окружности – есть середина гипотенузы.
Радиус R описанной окружности есть половина гипотенузы
Медиана, проведенная к гипотенузе, равна ее половине
Тригонометрические свойства
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
По сторонам
Углы равнобедренного треугольника, прилежащие к основанию, равны.
Биссектриса, медиана и высота, проведенные к основанию, совпадают.
Биссектриса, медиана и высота, проведенные из одной вершины, совпадают.
Равносторонний треугольник имеет центр — точка пересечения биссектрис, медиан, высот, центр описанной и вписанной окружностей.
Равные треугольники: Треугольники называют равными, если у них соответствующие стороны и углы равны
1 признак: По двум сторонам и углу между ними
2 признак: По стороне и двум прилежащим к ней углам
3 признак: По трем сторонам
Подобные треугольники — треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
1 признак: по двум пропорциональным сторонам и углу между ними
2 признак:по двум углам
3 признак: по трем пропорциональным сторонам
Замечательные линии треугольника
Биссектриса — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.
Все три биссектрисы треугольника пересекаются в одной точке.
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:
Высота — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.
Если AH и BM — прямые, содержащие высоты AH и BM треугольника ABC, то треугольники CHM и CAB подобны, коэффициент подобия равен модулю косинуса угла C.
Медиана- это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Все медианы треугольника пересекаются в одной точке, называемой центроидом (центром тяжести) треугольника
В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины: AO:OA1=BO:OB1=CO:OC1=2:1
Теорема косинусов квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Теорема синусов стороны треугольника пропорциональны синусам противолежащих углов.
Площадь треугольника
Формула Герона
Средняя линия треугольника- это отрезок, соединяющий середины двух его сторон.
Определение и применение углов бета
Значение солнечного бета-угла для спутника на околоземной орбите можно найти с помощью уравнения
- ,
где — истинная эклиптическая солнечная долгота, — долгота восходящего узла (LNA), — наклонение орбиты и — наклонение эклиптики (приблизительно 23,45 градуса для Земли сегодня). LNA и наклонение являются свойствами орбиты спутника, а солнечная долгота является функцией положения Земли на орбите вокруг Солнца (приблизительно линейно пропорционально дню года относительно дня весеннего равноденствия).
Приведенное выше обсуждение определяет бета-угол для спутников, вращающихся вокруг Земли, но бета-угол можно рассчитать для любой орбитальной системы из трех тел: то же определение можно применить, чтобы получить бета-угол для других объектов. Например, бета-угол спутника на орбите вокруг Марса по отношению к Земле определяет количество времени, в течение которого спутник находится на линии прямой видимости с Землей, то есть определяет, как долго Земля освещает спутник. как долго Земля скрыта от глаз. Тот же самый спутник также будет иметь бета-угол по отношению к Солнцу, и на самом деле он имеет бета-угол для любого небесного объекта, для которого вы хотите рассчитать: любой спутник, вращающийся вокруг тела (например, Земли), будет в тени этого тела. относительно данного небесного объекта (например, звезды) некоторое время, а в его поле зрения остальное время. Углы бета, описывающие негеоцентрические орбиты , важны, когда космические агентства запускают спутники на орбиты вокруг других тел в Солнечной системе.
Свойства и виды смежных углов в геометрии
- Так как две стороны смежных углов образуют прямую линию, то вместе они составляют развернутый угол. Его градусная мера составляет 180^\circ. Следовательно — сумма смежных углов тоже равна \(180^\circ.\)
- Если две прямые пересекаются, то они образуют две пары смежных углов: \(\angle1\) и \(\angle2\), \(\angle3\) и \(\angle4\), а также \(\angle1\) и \(\angle3\), \( \angle2\) и \(\angle4\). При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.
- У смежных углов одинаковые синусы.
- Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
- Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.
В парах действует правило: если один угол тупой, то другой обязательно будет острым.
Если один из углов правильный, то второй тоже правильный.
Внимание! Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до исключения). Если вы не можете написать работу самостоятельно, вы можете заказать ее здесь
Дано: \(\ угол \ альфа \) и \(\ угол \ бета \) смежны друг с другом и \(\ угол \ бета = 60 ^ \ окружность \).
Поиски: что такое \(\ угол ⌘ альфа ⌘)?
Если углы смежные, то
Ans: \(\;\ угол \альфа = 120 ^ \ круг \).
Дано: \(ዄ;ዄ угол \ альфа \) и \(ዄ;ዄ угол бета \) смежные и \(ዄ;ዄ угол \ альфа \) больше, чем \(ዄ;ዄ угол бета.ዄ) больше, чем \(30 ^ \ circ \).
Поиск: чему равны \(\ угол \ альфа) и \(\ угол \ бета. \)?
\При условии, что ዄ (ዄ угол \ бета = x \), то ዄ (ዄ угол \ альфа = x + 30 ^ \ окружность ዄ).
Поскольку сумма смежных углов равна 180 градусам, получаем следующее уравнение
Следовательно, значение 섹 (섹 угол \ бета = 75 ^ \ круг. 섹)
Для того чтобы найти значение \ (\ угол \ альфа \), необходимо произвести обычные вычисления по теореме о сумме.
Сравнение углов
- По виду угла. Любой острый угол меньше прямого и тупого угла. Прямые углы меньше тупых углов.
- Способ наложения одного угла на другой. Для определения равенства углов необходимо наложить один угол на другой таким образом, чтобы одна сторона одного угла совпала с одной стороной другого угла, в то время как две оставшиеся стороны оказались по одну сторону от совпавших сторон. В случае, если две оставшиеся стороны совпадают, углы полностью совпадают и, следовательно, равны. В противном случае, меньшим считается угол, который является частью другого. Таким образом, сравнивая стороны и учитывая их положение относительно друг друга, можно определить, равны ли углы или какой угол меньше а какой больше
- Измерением углов с помощью измерительных приборов.
Кратная вводная
Для работы с перпендикулярными прямыми нам потребуются два вида углов: смежные и вертикальные.
1.1.Смежные углы
Вот пример смежных углов с общей стороной $MN$:
Основное свойство таких углов: их сумма всегда равна 180°:
Таким образом, зная один смежный угол, мы тут же найдём другой.
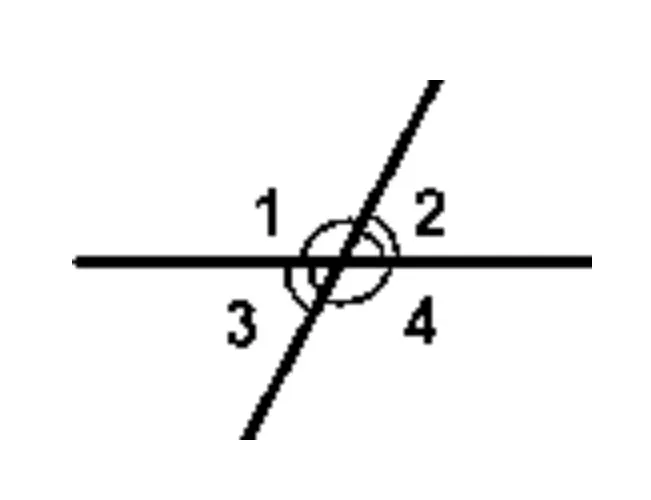
1.2. Вертикальные углы
На самом деле на пересечении двух прямых возникает сразу две пары таких углов:
Вертикальные углы всегда равны — и это их главное свойство. На рисунке мы видим, что $\angle 1=\angle 3$ и $\angle 2=\angle 4$.
1.3. Какие бывают углы
И вообще, нам пока известны четыре типа углов: острый, прямой, тупой и развёрнутый.
Интересное свойство прямого угла: если при пересечении двух прямых возник прямой угол, то все остальные углы (вертикальные, смежные с ним) тоже будут прямыми. И вот тут мы переходим к основной теме урока.
Что создает подъемную силу самолета?
Подъемная сила самолета создается крылом, которое является одним из важнейших его компонентов.
Крыло спроектировано таким образом, что, когда по нему обтекает воздух, происходит разница давлений на его верхней и нижней поверхностях. Верхняя поверхность крыла слегка выпуклая, а нижняя — вогнутая, что придает воздуху, проходящему над крылом более длинный путь, чем воздуху, проходящему под ним.
Из-за разницы в скорости потока воздуха, давление на верхней поверхности крыла становится ниже, чем на нижней. Это создает разность давлений, которая направлена вверх, что и составляет подъемную силу.
- Аэродинамическое качество крыла представляет собой отношение подъемной силы к лобовому сопротивлению.
- Чем выше аэродинамическое качество, тем эффективнее крыло.
- На аэродинамическое качество крыла влияет множество факторов, включая форму, размеры и материалы.
Фактчек
Чтобы решать сложные тригонометрические уравнения и неравенства, необходимо уметь преобразовывать выражения. Для этого нужно правильно пользоваться формулами.
Условно, формулы можно разделить на несколько групп: основные формулы тригонометрии, формулы отрицательных углов, формулы двойных углов, формулы сложения и вычитания углов, формулы понижения степени, формулы для суммы, разности и произведения синусов и косинусов.
К основным тригонометрическим формулам в первую очередь относится основное тригонометрическое тождество: \(sin^2x + cos^2x = 1\)
Оно и еще несколько других формул раскрывают связь между функциями.
Важно запомнить, что формулы работают в обе стороны: их можно читать справа налево и слева направо. Более того, многие формулы можно выводить друг из друга, что значительно упрощает их заучивание.
Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.
Для решения тригонометрических уравнений необходимо применять аркфункции, то есть функции, обратные тригонометрическим
С помощью аркфункций мы находим угол через значение тригонометрической функции.
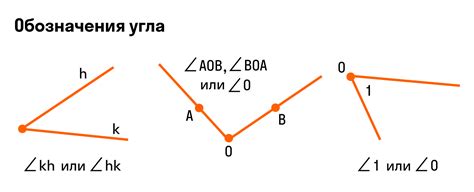
Сравнение способов обозначения угла
Угол может быть обозначен различными способами, включая градусы, минуты и секунды, радианы и прямые углы. Каждый из этих способов имеет свои особенности и применяется в различных областях математики и науки.
Градусы, минуты и секунды:
Самый распространенный способ обозначения угла — это использование градусов, минут и секунд. Угол измеряется в градусах, затем каждый градус делится на 60 минут, а каждая минута — на 60 секунд. Например, если угол равен 45 градусам, 30 минутам и 15 секундам, его обозначение будет выглядеть как 45° 30′ 15″. Этот способ позволяет точно измерить углы и использовать их при работе с картами, навигацией, астрономией и другими областями, требующими высокой точности измерений.
Радианы:
В физике и математике, также широко используется обозначение угла в радианах. Радиан — это мера угла, которая определяется отношением длины дуги к радиусу окружности. В одном радиане есть примерно 57,3 градусов, но при работе с радианами угол измеряется используя пи (π) вместо числа 180, что делает вычисления более удобными. Обозначение угла в радианах просто: если угол равен, например, π/4 радиан, его можно записать как 45° или 90° (так как градусы привычнее).
Прямые углы:
Прямой угол — это угол, равный 90 градусам или π/2 радианам. Обозначение прямого угла может быть сделано соответствующим символом, например, «∠». Прямой угол используется в геометрии для обозначения перпендикулярных линий и поворотов.
Каждый из этих способов обозначения угла имеет свое преимущество и может быть использован в зависимости от конкретной ситуации и требований
Важно понимать эти способы и уметь переводить углы из одной системы обозначения в другую
Смежные углы
Смежные углы – это углы, имеющие общую сторону и вершину. Они лежат на одной прямой и дополняют друг друга до 180 градусов.
Основные свойства смежных углов:
- Они суммируются до 180 градусов: α + β = 180°.
- У них общая вершина.
- Они расположены на одной прямой.
Смежные углы являются частным случаем смежных углов. Если углы находятся на одной прямой, но они не дополняют друг друга до 180 градусов, то они являются обычными смежными углами.
Примеры смежных углов:
- Углы при соединении двух сторон прямоугольного треугольника.
- Углы при пересечении двух прямых, образующих прямой угол.
- Углы примыкающих сторон, образующих многоугольник.
Размеры смежных углов могут быть разными. Они могут быть как острыми, так и тупыми.
Смежные углы широко применяются в геометрии для решения задач и вычислений. Они помогают определить неизвестные углы, выявить параллельность или перпендикулярность прямых.




























