Координатная прямая. координатная плоскость

Введение в пересекающиеся линии и прямоугольники

Пересекающиеся линии и прямоугольники являются двумя фундаментальными геометрическими концепциями, которые широко используются во многих областях, включая архитектуру, инженерию, дизайн и искусство.Когда линии пересекаются, они образуют углы и точки, которые можно использовать для создания сложных узоров и форм.Прямоугольники — это тип многоугольника с четырьмя сторонами, четырьмя вершинами и четырьмя прямыми углами.Когда прямоугольники пересекаются, они образуют интересные формы и пространства, которые можно использовать для создания функциональных и эстетически приятных дизайнов.В этом разделе мы подробно рассмотрим концепцию пересекающихся линий и прямоугольников и обсудим их свойства и приложения.

Вот некоторые идеи о пересекающихся линиях и прямоугольниках из разных точек зрения:

С математической точки зрения пересекающиеся линии и прямоугольники являются важными понятиями в геометрии.Они используются для определения углов, точек и полигонов и изучения своих свойств и отношений.Например, пересечение двух линий может использоваться для расчета наклона, направления и расстояния между ними, в то время как пересечение двух прямоугольников может использоваться для расчета их площади, периметра и перекрывающейся области.

С архитектурной точки зрения пересекающиеся линии и прямоугольники используются для создания функциональных и визуально привлекательных пространств.Они используются для определения формы и расположения зданий, комнат и мебели, а также для создания узоров и текстур на стенах, полах и потолках.Например, пересечение двух стен можно использовать для создания уголка или ниши, в то время как пересечение двух этажей можно использовать для создания шага или рампы.

С художественной точки зрения пересекающиеся линии и прямоугольники используются для создания абстрактных и выразительных композиций.Они используются для создания шаблонов, текстур и форм, которые вызывают эмоции и идеи, а также для изучения отношений между формой и пространством.Например, пересечение двух линий можно использовать для создания креста или звезды, в то время как пересечение двух прямоугольников можно использовать для создания сетки или лабиринта.

Вот некоторая углубленная информация о пересекающихся линиях и прямоугольниках:

1. Пересечение линий: когда пересекаются две линии, они образуют четыре угла, которые имеют разные свойства и имена.Углы называются вертикальными углами, прилегающими углами, альтернативными углами и соответствующими углами.Вертикальные углы противоположны друг другу и имеют одинаковую меру, в то время как соседние углы находятся рядом друг с другом и имеют общую сторону.Альтернативные углы находятся на противоположных сторонах поперечного уровня и имеют одинаковую меру, в то время как соответствующие углы находятся на одной и той же стороне поперечного отдела и имеют одинаковую меру.

2. Пересечение прямоугольников: когда два прямоугольника пересекаются, они образуют четыре области, которые имеют разные свойства и имена.Регионы называются перекрывающейся областью, непересекающейся областью, общим преимуществом и общей вершиной.Перекрывающаяся область-это область, которая является общей для обоих прямоугольников, в то время как непересекающая область-это область, которая принадлежит только к одному прямоугольнику.Общий край — это край, который является общим для обоих прямоугольников, в то время как общая вершина является вершиной, которая является общей для обоих прямоугольников.

3. Применение пересекающихся линий и прямоугольников: пересекающиеся линии и прямоугольники имеют много применений в разных полях.В архитектуре они используются для создания функциональных и эстетически приятных пространств, таких как углы, ниши и шаги.В инженерии они используются для расчета свойств и взаимосвязи геометрических фигур, таких как область, периметр и объем.В искусстве они используются для создания абстрактных и выразительных композиций, таких как узоры, текстуры и формы.

Таким образом, пересекающиеся линии и прямоугольники являются важными понятиями в геометрии, архитектуре, инженерии и искусстве.Они используются для определения углов, точек, полигонов и пространств, а также для создания функциональных и эстетически приятных дизайнов.Понимая их свойства и приложения, мы можем использовать их для решения проблем и создания красивых и значимых композиций.

Введение в пересекающиеся линии и прямоугольники — пересекающиеся линии: когда линии пересекаются: прямоугольники и пересечения

Понятие перпендикуляра

Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.

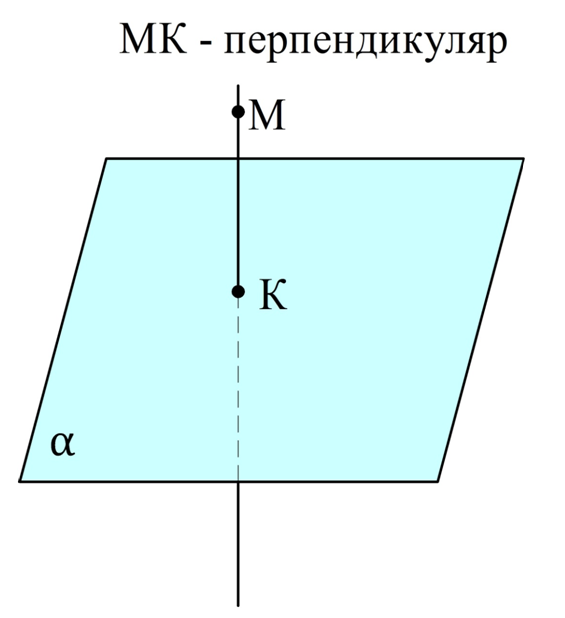
Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:

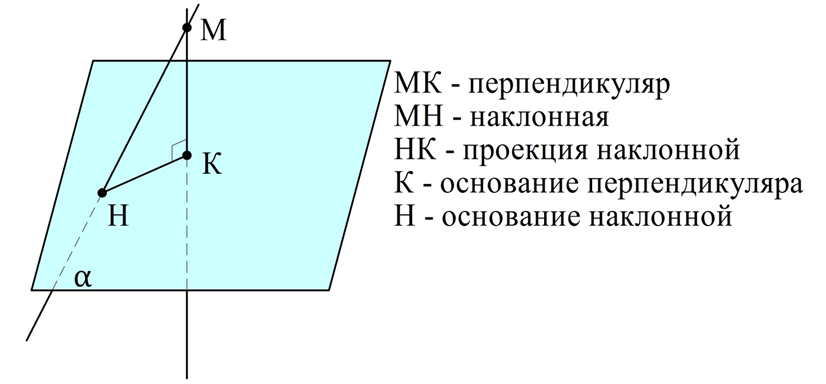
Запомним некоторые геометрические термины. В таком построении:

• отрезок МН – это наклонная;
• отрезок НК – это проекция наклонной, или просто проекция;
• К – основание перпендикуляра;
• Н – основание наклонной.

Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).

Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.

2.5. Следы прямой

След прямой – точка пересечения прямой с плоскостью проекций.

Прямая общего положения в общем случае может быть три следа:

• горизонтальный след M₁– точка пересечения прямой с горизонтальной плоскостью проекций π₁;
• фронтальный след N₂– точка пересечения прямой с фронтальной плоскостью проекций π₂;
• профильный  след L₃ – точка пересечения прямой с профильной плоскостью проекций π₃.

След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

• горизонтальный след совпадает со своей горизонтальной проекцией M≡M₁,
• фронтальный – с фронтальной проекцией N≡N₂,
• профильный – с профильной проекцией L≡L₃ (Рисунок 2.10).

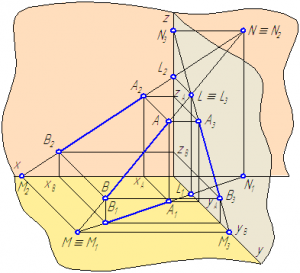
Рисунок 2.10 – Построение следов отрезка прямой АВ

Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

Для построения горизонтального следа прямой АB необходимо:

1. Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М₂ является фронтальной проекцией горизонтального следа;
2. Из точки М₂ провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М₁ и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.

Чтобы построить фронтальный след отрезка АB прямой, необходимо:

1. Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N₁ является горизонтальной проекцией фронтального следа;
2. Из точки N₁ провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB  или ее продолжением. Точка пересечения N₂ и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.

Ниже приводим алгоритм построения следов отрезка прямой АВ:

A₁B₁ ∩ xO =N₁;       Y_N=0;                   N ∈ xOz (π₂)      ⇒      AB ∩ xOz=N

A₂B₂ ∩ xO =M₂;       Z_M=0;                  M ∈ xOy (π₁)     ⇒      AB ∩ xOy=M

A₁B₁ ∩ yO =L₁;        X_L=0;                   L ∈ yOz (π₃)     ⇒      AB ∩ yOz=L

A₂B₂ ∩ zO =L₂;

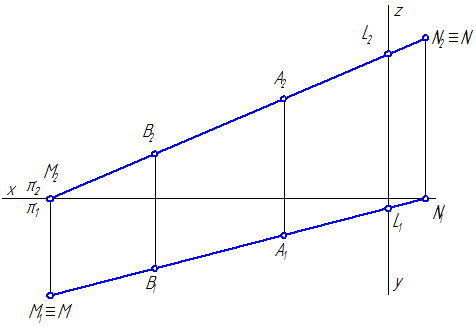Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

Применение пересекающихся прямых в реальных задачах

Пересекающиеся прямые являются важным понятием в геометрии и математике в целом. Они имеют широкое применение в различных задачах и областях, как теоретических, так и практических.

1. Графики функций:

Пересечение графиков функций является ключевым моментом при решении уравнений и систем уравнений. Если графики двух функций пересекаются, то это означает, что существует точка (или точки), в которой значения этих функций равны друг другу. Это может быть полезно для определения корней уравнений или нахождения точек пересечения кривых.

2. Статистика и анализ данных:

Пересекающиеся прямые используются в анализе данных для определения зависимостей и взаимосвязей различных переменных. Например, в задачах линейной регрессии, где исследуется зависимость одной переменной от другой, пересечение прямой регрессии с осью ординат может указывать на начало или нулевое значение зависимой переменной.

3. Проектирование и архитектура:

Пересекающиеся прямые используются в проектировании и архитектуре для определения точек пересечения или соприкосновения различных элементов. Например, в строительстве пересечение линий может указывать на место сопряжения стен и потолка, или на точки пересечения строительных элементов.

4. Геодезия и навигация:

Геодезисты и навигаторы также используют пересекающиеся прямые для определения координат точек на местности. Путем измерений и пересечения линий, например, с помощью триангуляции, можно определить координаты точек и точное положение объектов.

Таким образом, пересекающиеся прямые являются мощным инструментом в решении различных задач и помогают анализировать и понимать различные взаимосвязи и зависимости в реальном мире.

Как обозначить прямую

Прямая линия обычно обозначается маленькой латинской буквой.

Линия, на которой отмечены две точки, иногда обозначается большими латинскими точками, соответствующими названиям этих точек.

• На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F лежат на одной прямой, поэтому прямая DE, прямая EF и прямая DF — это три разных названия одной и той же прямой.

Задача № 1 из учебника Атанасян 7-9 класс

Постройте прямую, обозначьте ее буквой a и отметьте точки A и B на этой прямой, а также точки P, Q и R, которые не лежат на этой прямой. Опишите взаимное расположение точек A, B, P, Q, R и прямой a с помощью символов ∈ и ∉ .

Типы пересечений в прямоугольниках

Когда дело доходит до прямоугольников, пересекающиеся линии играют решающую роль в определении типа происходящего пересечения.Существуют различные типы пересечений в прямоугольниках, каждый из которых с его уникальными свойствами и характеристиками.Понимание этих типов пересечений имеет жизненно важное значение для решения математических задач и создания конструкций, которые включают прямоугольники.С разных точек зрения прямоугольники могут иметь разные ориентации, которые влияют на то, как их линии пересекаются.Горизонтальные и вертикальные линии пересекаются по -разному по сравнению с другими ориентациями.Следовательно, важно иметь обзор типов пересечений, которые происходят в прямоугольниках. 1

Пересечение точки: этот тип пересечения происходит, когда две линии пересекаются в одной точке.Например, когда горизонтальная линия пересекает вертикальную линию, они образуют точку пересечения.Точка пересечения является единственной точкой, где две линии встречаются, и она не имеет длины или ширины.Он представлен точкой или крестом, где пересекаются линии

1. Пересечение точки: этот тип пересечения происходит, когда две линии пересекаются в одной точке.Например, когда горизонтальная линия пересекает вертикальную линию, они образуют точку пересечения.Точка пересечения является единственной точкой, где две линии встречаются, и она не имеет длины или ширины.Он представлен точкой или крестом, где пересекаются линии.

2. Сегмент пересечения: когда две линии пересекаются, они образуют сегмент линии.Линейный сегмент имеет две конечные точки и определенную длину.В прямоугольнике сегмент линии может быть стороной прямоугольника или внутреннего сегмента.Например, когда диагональная линия пересекает горизонтальную линию, они образуют сегмент линии, который является частью интерьера прямоугольника.

3. Пересечение лучей: этот тип пересечения происходит, когда линия пересекает другую линию, а одна из линий простирается на неопределенный срок.Луч имеет одну конечную точку и простирается бесконечно в одном направлении.В прямоугольнике луч может быть стороной прямоугольника или внутреннего лучей.Например, когда диагональная линия пересекает вертикальную линию, они образуют луч, который распространяется на бесконечность в одном направлении.

4. Нет пересечения: иногда две линии в прямоугольнике не пересекаются.В этом случае они параллельны друг другу.Параллельная линия имеет тот же наклон, что и другая линия, и никогда не пересекает ее.Например, горизонтальная линия и диагональная линия в прямоугольнике параллельны друг другу и никогда не пересекаются.

понимание различных типов пересечений в прямоугольниках имеет важное значение для решения математических задач и создания дизайна.Каждый тип пересечения обладает своими уникальными свойствами и характеристиками, которые делают его полезным в разных приложениях.Зная различные типы пересечений, вы можете легко идентифицировать их в прямоугольнике и использовать их в своих интересах. Типы пересечений в прямоугольниках — пересекающиеся линии: когда линии пересекаются: прямоугольники и пересечения

Типы пересечений в прямоугольниках — пересекающиеся линии: когда линии пересекаются: прямоугольники и пересечения

Понимание концепции пересечений

Перекрестки являются фундаментальной концепцией, которая играет важную роль в геометрии.Это точка, где встречаются две или более линий или кривых.В мире геометрии пересечения происходят в различных формах и размерах.Это может быть пересечение двух прямых линий, сходимость изогнутых линий или встреча двух плоскостей.Понимание концепции пересечений имеет решающее значение для понимания многих геометрических фигур и форм.Это помогает в анализе форм и поиске решений проблем, связанных с геометрией.В этом разделе мы углубимся в концепцию пересечений и то, что они влечет за собой.

Вот некоторые понимания предмета:

1. Перекрестки происходят, когда две или более линий или кривых пересекаются друг с другом в определенной точке.Точка пересечения необходима для определения свойств линий и кривых.Например, точка пересечения двух прямых линий может помочь рассчитать угол между ними.

2. Перекрестки могут происходить под разными углами, создавая разные формы.Например, когда две прямые линии пересекаются под прямым углом, они образуют квадрат или прямоугольник.Когда две линии пересекаются под острым углом, они образуют треугольник, а пересечение под тупящим углом образует тупой треугольник.

3. Перекрестки также могут происходить в 3D -формах.В этом случае точка пересечения — это то, где встречаются две или более плоскости.Например, когда два плоскости пересекаются, они образуют линию.Точно так же, когда пересекаются три плоскости, они образуют точку.

4

Концепция пересечений имеет важное значение в различных областях, включая архитектуру, инженерию и дизайн.Например, понимание того, как пересекаются линии и кривые, может помочь в разработке зданий и мостов

Таким образом, пересечения являются критической концепцией в геометрии.Они помогают определить свойства линий и кривых, и их точка пересечения необходима для анализа геометрических фигур.От прямых линий до изогнутых линий и трехмерных форм, пересечения играют значительную роль в определении различных форм и дизайнов.

Понимание концепции пересечений — пересекающиеся линии: когда линии пересекаются: прямоугольники и пересечения

Виды пересечения двух прямых

Пересечение прямых – это точка или несколько точек общего расположения двух прямых в одной плоскости.

Если две прямые пересекаются в одной точке, то такое пересечение называется простым. Это означает, что две прямые сходятся к одной точке, а также что эта точка является единственной общей для обеих прямых. Это свойство никогда не меняется, независимо от величины углов, которые образуют эти прямые.

Если две прямые не пересекаются, то такое пересечение называется параллельным. Две прямые в одной плоскости называются параллельными, если они не имеют общих точек.

Если две прямые находятся в одной плоскости и пересекаются под одним и тем же углом, то такое пересечение называется скошенным. В таком случае обе прямые пересекаются не в одной точке, а по двум симметричным точкам симметрии, которые находятся на средней перпендикулярной между этими двумя прямыми.

Важно отметить, что прямые могут иметь бесконечное количество пересечений, если они совпадают, т.д

Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века

Что такое линия? В чем разница между различными кривыми? Математики задаются этими вопросами уже 2500 лет, и путь к ответам на них не был лишен драматизма — открытие иррациональных отрезков прямых, согласно легенде, стало трагедией для пифагорейцев, а открытие заполняющих площадь кривых Пеано в начале 20 в. Математик и художник Дэвид Кац об истории понятия «кривые» в древней и средневековой математике и в современном математическом анализе.

Интерес человека к прямым и кривым линиям прослеживается с древности. Мы видим всевозможные кривые в геометрических узорах в керамике и архитектуре. Помимо довольно простых узоров, состоящих из прямых линий, часто встречаются и более сложные: спирали, волнистые линии и многое другое.

Концепции геометрии уже существовали в Египте и в цивилизациях Плодородного полумесяца

Очевидно, они возникли из очень практических потребностей: например, для сельского хозяйства было важно иметь возможность измерять площадь земли. Однако в сохранившихся источниках мы находим эти понятия скорее как набор рецептов, чем как науку

Реальные приложения пересекающихся линий в прямоугольниках

Пересекающиеся линии в прямоугольниках имеют широкий спектр реальных приложений.Они обычно используются в архитектуре, технике и строительстве.В архитектуре пересекающиеся линии используются для разработки макетов здания, создания планов этажей и определения размещения дверей и окон.Инженеры используют пересекающиеся линии для проектирования мостов, дорог и автомагистралей, чтобы они были безопасными и структурно звучащими.В конструкции пересекающиеся линии используются для измерения и размещения расположения стен, полов и потолков.

Вот некоторые реальные приложения пересекающихся линий в прямоугольниках:

1. плотницкие и деревообрабатывающие : пересекающиеся линии используются для измерения и выделения углов в плотницке и деревообработке.Например, при строительстве лестницы пересекающиеся линии используются для обеспечения того, чтобы каждый шаг был одинаковым размером и углом.

2. Графический дизайн : в графическом дизайне пересекающиеся линии используются для создания сетей, которые используются для выравнивания текста и изображений.Это помогает создать чистую и организованную планировку.

3. математика : пересекающиеся линии в прямоугольниках используются в геометрии, чтобы определить длину, ширину и площадь прямоугольника.Они также используются для расчета угла пересечения между двумя линиями.

4. компьютерное программирование : пересекающиеся строки используются в компьютерном программировании для создания форм и графики.Например, программист может использовать пересекающиеся линии для создания прямоугольника или треугольника.

Пересекающиеся линии в прямоугольниках имеют многочисленные реальные приложения.Они используются в различных областях, таких как архитектура, инженерия, строительство, столярные изделия, деревообработка, графический дизайн, математика и компьютерное программирование.Понимание пересекающихся линий и их применений важно для всех, кто интересуется этими областями. Реальные приложения пересекающихся линий в прямоугольниках — пересекающиеся линии: когда линии пересекаются: прямоугольники и пересечения

Реальные приложения пересекающихся линий в прямоугольниках — пересекающиеся линии: когда линии пересекаются: прямоугольники и пересечения

Свойства перпендикулярных прямых

Сначала разберём два «стандартных» свойства, которые вы найдёте в любом учебнике геометрии 7-го класса. А затем — одно «нестандартное», но именно оно чаще всего и встречается в настоящих задачах.

3.1. Теорема о двух прямых, перпендикулярных третьей

Прямая $AB\bot EF$ и прямая $MN\bot EF$. Следовательно, прямые $AB$ и $MN$ не пересекаются. Проще говоря, они параллельны (см. урок «Параллельные прямые»).

3.2. Теорема о прямой, перпендикулярной данной

Доказательство этой теоремы состоит из двух частей: сначала докажем, что такую прямую провести можно, а затем — что она единственная.

Прямая, перпендикулярная данной, строится очень просто. Рассмотрим прямую $a$, на которой отмечена точка $M$:

Отложим от луча $MK$ угол, равный 90°. В любую сторону: в верхнюю полуплоскость или нижнюю — не имеет значения. Получим луч $MN$:

Наконец, продолжим луч $MN$ в противоположную другую сторону (т.е. построим дополнительный луч). Получим искомую прямую $MN\bot a$:

Единственность такого построения следует либо из аксиомы о том, что нужный угол можно отложить в нужном направлении одним и только одним способом, либо из предыдущей теоремы о двух прямых, перпендикулярных данной. В самом деле, пусть есть ещё одна прямая $ML$, которая, как и $MN$, перпендикулярна прямой $a$:

Поскольку $MN\bot a$ и $ML\bot a$, по предыдущей теореме эти прямые не пересекаются. Что противоречит нашему построению, в котором у прямых $MN$ и $ML$ есть общая точка $M$. Следовательно, прямые $MN$ и $ML$ совпадают, что и требовалось доказать.

3.3

Важное свойство прямого угла. Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах

Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Это утверждение может показаться очевидным. И оно действительно является таковым. Однако деление прямого угла на части встречается в задачах настолько часто, что я не мог не упомянуть об этом.

Кроме того, начинающие ученики часто не замечают такие углы на чертежах. Поэтому сейчас мы будем отрабатывать эту теорему на реальных задачах.

Определение перпендикулярных прямых

Перпендикулярные прямые.

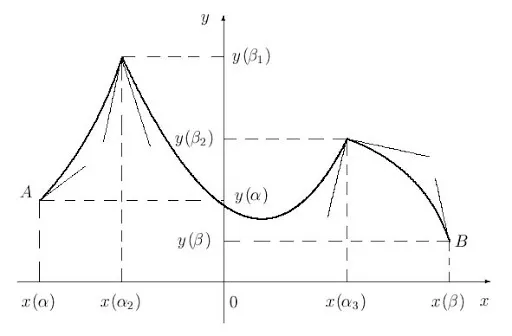
Пусть а и b — прямые, пересекающиеся в точке А (рис. 1). Каждая из этих прямых точкой А делится на две полупрямые. Полупрямые одной прямой образуют с полупрямыми другой прямой четыре угла. Пусть альфа — один из этих углов. Тогда любой из остальных трех углов будет либо смежным с углом альфа, либо вертикальным с углом альфа.

Отсюда следует, что если один из углов прямой, то остальные углы тоже будут прямые, В этом случае мы говорим, что прямые пересекаются под прямым углом.Определение.Две прямые называются перпендикулярными, если они пересекаются под прямым углом (рис. 2).

Перпендикулярность прямых обозначается знаком ⊥ Запись а ⊥ b читается: Прямая а перпендикулярна прямой b.Теорема.

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

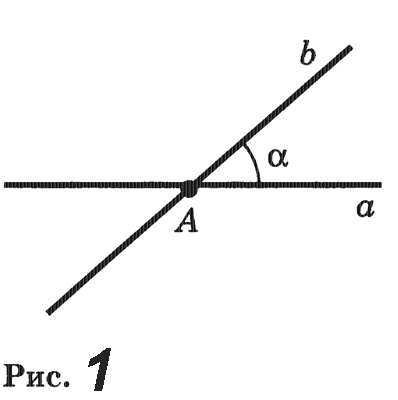
Доказательство.Пусть а — данная прямая и А — данная точка на ней. Обозначим через ах одну из полупрямых прямой а с начальной точкой А (рис. 3). Отложим от полупрямой а1 угол  (a1b1), равный 90°.Тогда прямая, содержащая луч b1, будет перпендикулярна прямой а.

Допустим, что существует другая прямая, проходящая через точку А и перпендикулярная прямой а. Обозначим через с1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b2. Углы (a1b1) и (a1c1), равные каждый 90°, отложены в одну полуплоскость от полупрямой а1. Но от полупрямой а1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не может быть другой прямой, проходящей через точку А и перпендикулярной прямой а. Теорема доказана.

Определение.

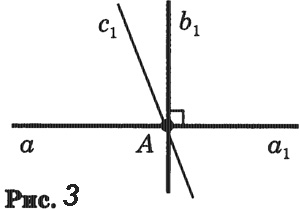
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.На рисунке 4 перпендикуляр АВ проведен из точки А к прямой а. Точка В — основание перпендикуляра.

Для построения перпендикуляра пользуются чертежным угольником (рис. 5).

Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Перпендикулярность прямых АС и ВD обозначается так: АС ⊥ ВD (читается: «Прямая АС перпендикулярна к прямой ВD»).Отметим, что две прямые, перпендикулярные к третьей, не пересекаются (рис. 6,а). В самом деле, рассмотрим прямые АА1 и ВВ1, перпендикулярные к прямой РQ (рис. 6,б). Мысленно перегнем рисунок по прямой РQ так, чтобы верхняя часть рисунка наложилась на нижнюю. Так как прямые углы 1 и 2 равны, то луч РА наложится на луч РА1. Аналогично, луч QВ наложится на луч QB1. Поэтому, если предположить, что прямые АА1 и ВВ1 пересекаются в точке М, то эта точка наложится на некоторую точку М1 также лежащую на этих прямых (рис. 6,в), и мы получим, что через точки М и М1 проходят две прямые: АА1 и ВВ1. Но это невозможно. Следовательно, наше предположение неверно и, значит, прямые АА1 и ВВ1 не пересекаются.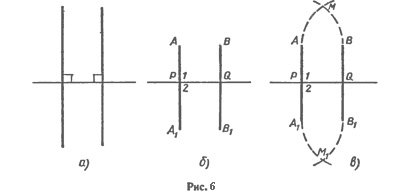

Угол между плоскостями

Во-первых, мы можем использовать геометрические методы. Если мы знаем что-то о дополнительных углах, мы можем соотнести их с искомым углом, используя свойства одинаковых или похожих фигур. Например, если мы знаем стороны треугольника и нам нужно вычислить угол между прямыми линиями, на которых лежат эти стороны, достаточно теоремы косинусов. Если это правильный треугольник, то полезно знать синус, косинус и тангенс угла.

Метод координат также очень полезен для решения таких задач. Давайте объясним, как правильно его использовать.

У нас есть прямоугольная (декартова) система координат O x y, с двумя прямыми. Обозначим их через a и b. Линии могут быть описаны определенными уравнениями. Исходные прямые имеют точку пересечения М. Как определить требуемый угол (обозначим его через a ) между двумя прямыми?

Начнем с основного принципа определения угла, заданного σ

• Простейшие тригонометрические неравенства
• Площадь ортогональной проекции многоугольника
• Задание №16. Досрочный ЕГЭ 2018
• Вектора. Часть 1
• Логарифмическая функция
• Прямоугольный треугольник

Понятие перпендикулярных прямых

Углы бывают острые, прямые и тупые.

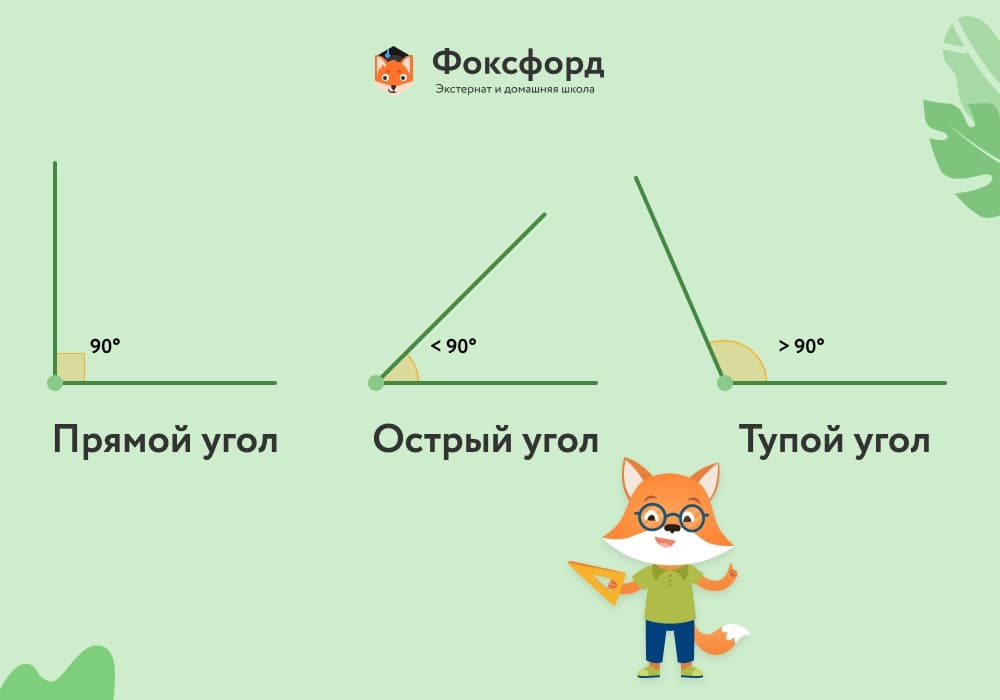
Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

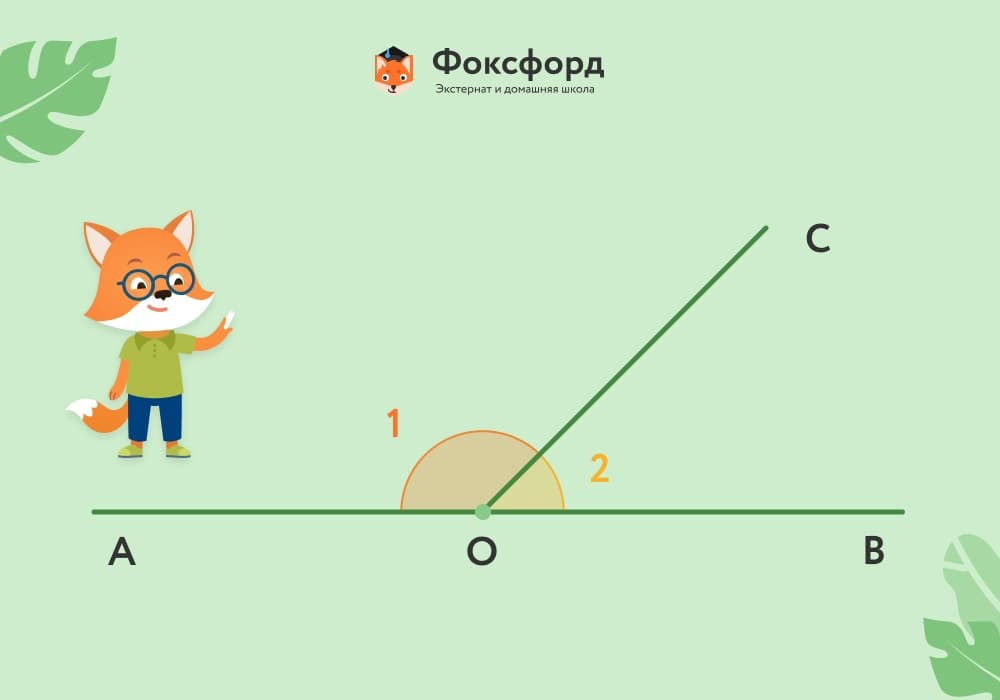
На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

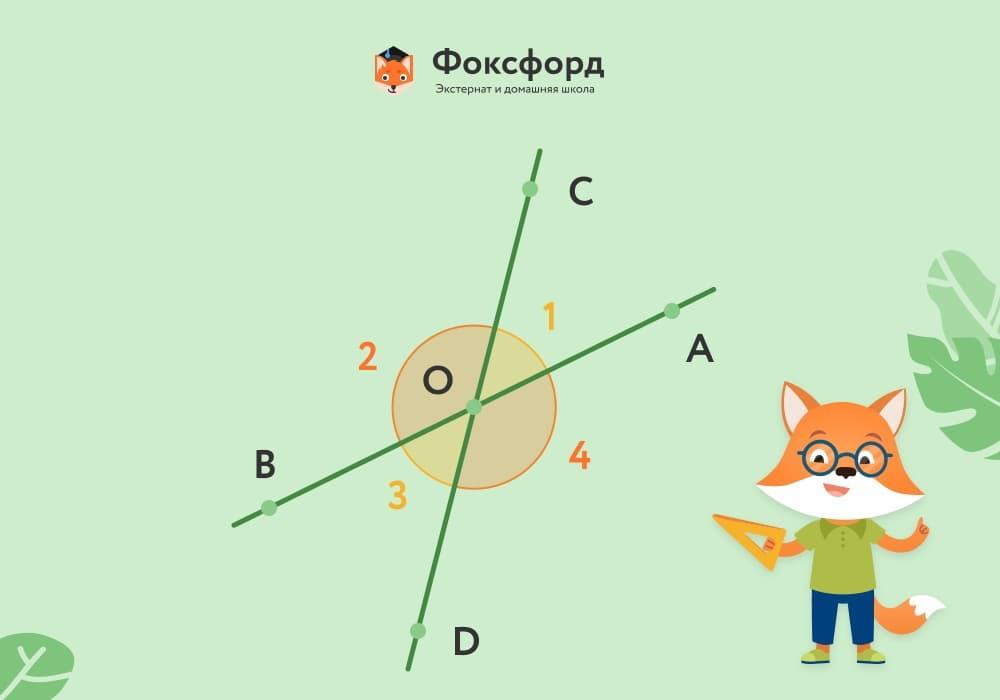
Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:∡1 + ∡2 = 180°∡1 + ∡4 = 180°∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

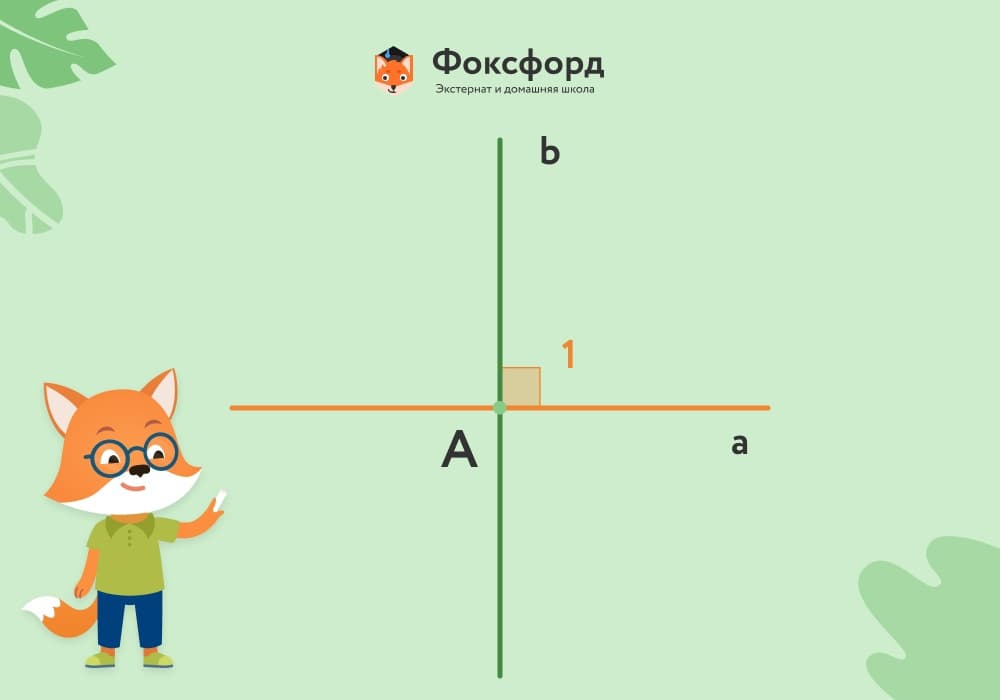
∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Определение перпендикулярных прямых

Мы готовы ответить, какие прямые называются перпендикулярными:

Чтобы доказать, что каждый из углов будет прямым, разметим на чертеже оставшиеся углы — углы $\beta$, $\gamma$ и $\delta$. Применим к ним доказанные нами ранее теоремы о вертикальных и смежных углах, при условии, что определение перпендикулярных прямых задает $\angle{\textcolor{purple}{\alpha}}=90^\circ.$

Доказательство

Угол $\beta$ — смежный с углом $\alpha$. Известно, что сумма смежных углов равняется $180^{\circ}$. Если угол $\alpha=90^{\circ}$, то получаем, что:

$$\beta=180^{\circ}-90^{\circ}=90^{\circ}$$

Вертикальные углы равны. Угол $\beta$ вертикален углу $\delta$, следовательно угол $\delta$ так же, как и $\beta$, равняется $90^{\circ}$. Аналогичное применимо и к другой паре вертикальных углов — углам $\alpha$ и $\gamma$.

Имеем:

$$\begin{cases}\alpha=90^{\circ}\\\beta=90^{\circ}\\\gamma=90^{\circ}\\\delta=90^{\circ}\end{cases}$$

Перпендикулярные прямые при пересечении образуют только прямые углы. Что и требовалось доказать.

{"questions":[{"content":"`image-1`Проверим, внимательны ли вы. Прямой угол на чертежах имеет индикацию, отличающуюся от прочих углов. Так ли это? `choice-10`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/09/perp-question.svg"},"choice-10":{"type":"choice","options":,"explanations":["<i>А вы внимательно смóтрите на чертежи. Наше почтение!</i>",""],"answer":}}}]}