Геометрия

Что такое векторы сонаправлены

Векторы сонаправлены — это понятие из линейной алгебры, которое описывает взаимное расположение двух или более векторов на одной прямой. Когда векторы сонаправлены, это означает, что они направлены в одну и ту же сторону и могут быть представлены как коллинеарные векторы.

Векторы сонаправлены имеют одинаковое направление, но могут отличаться по длине и ориентации. Направление вектора может быть положительным или отрицательным, в зависимости от того, в какой стороне он направлен относительно оси.

Векторы сонаправлены широко используются в физике, где они помогают описать движение объектов в пространстве. Например, при описании движения автомобиля по прямой дороге, вектор скорости и вектор ускорения будут сонаправлены, так как они указывают в том же направлении движения.

Другой пример векторов сонаправлены — это силы, действующие на объект. Если на объект действуют несколько сил, и их векторы сонаправлены, то можно сложить эти векторы для получения общей силы, действующей на объект.

Для определения того, что векторы сонаправлены, достаточно проверить, совпадают ли их направления. Если векторы направлены в одну и ту же сторону или противоположны друг другу, то они сонаправлены и могут быть представлены как коллинеарные векторы.

Пример:

1. Вектор A = (3, 4) и вектор B = (6, являются сонаправленными, так как они имеют одинаковое направление и могут быть умножены на одно и то же число.
2. Вектор C = (-2, 1) и вектор D = (-4, -2) также являются сонаправленными, так как они имеют противоположное направление.
3. Вектор E = (1, 3) и вектор F = (-1, -3) не являются сонаправленными, так как они имеют противоположное направление.

Векторы сонаправлены являются важным понятием в линейной алгебре и находят применение в различных областях науки и техники.

Определение и применение сонаправленного вектора

Сонаправленный вектор – это вектор, направленный в том же направлении, что и другой вектор. Он имеет ту же точку приложения и ту же длину, что и данный вектор. Сонаправленный вектор может иметь только направление и длину, без точки приложения.

Сонаправленный вектор встречается часто в математике, физике и других науках. Он может использоваться для вычисления различных физических величин, например, скорости, ускорения, силы и многих других. Он также может применяться для определения соотношения между двумя векторами.

Одним из примеров применения сонаправленного вектора в физике является расчет момента силы. Момент силы – это произведение вектора силы на перпендикулярное расстояние от точки приложения силы до оси вращения. Для вычисления момента силы необходимо знать направление вектора силы и перпендикулярное расстояние, которое можно найти, используя сонаправленный вектор.

В заключение, сонаправленный вектор – это важный инструмент для работы с векторами и вычисления различных физических величин. Он позволяет определить направление и длину вектора и применять его в различных ситуациях, где требуется вычисление момента силы, скорости и многих других физических величин.

Как правильно пишется слово «сонаправленный»

сонапра́вленный

сонапра́вленный; кр. ф. -ен, -ена

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Я стал чуточку лучше понимать мир эмоций.

Вопрос: декаданс — это что-то нейтральное, положительное или отрицательное?

Предложения со словом «сонаправленный»

• Цель «Укрепить внутреннюю корпоративную культуру компании, внедрить понятие „внутреннего клиента“, необходимости эффективных коммуникаций между подразделениями для достижения целей предприятия» – за этот год практически весь процесс деятельности предприятия приобрёл сонаправленный вектор движения.
• (все предложения)

Сонаправленные векторы: применение в геометрии

В геометрии сонаправленные векторы часто используются для решения различных задач. Они помогают определить направление прямой или плоскости, найти положение точки относительно заданного направления, а также решить задачи на нахождение углов и расстояний.

Применение сонаправленных векторов в геометрии позволяет легче представлять и анализировать геометрические объекты. Например, при решении задач на построение или нахождение координат точек используются свойства сонаправленных векторов. Они также помогают в понимании симметрии и сопряженных фигур.

Благодаря сонаправленным векторам можно упростить решение геометрических задач и получить точные результаты. Например, при нахождении векторных произведений объединение нескольких сонаправленных векторов дает возможность умножить их модули и получить модуль суммы этих векторов.

Важно помнить, что для двух векторов считаются сонаправленными, если они параллельны и имеют одинаковое направление. Если же векторы параллельны, но направления противоположны, то они считаются противоположно сонаправленными

Таким образом, сонаправленные векторы — это важный инструмент в геометрии, который позволяет более точно анализировать геометрические объекты и решать задачи, связанные с их положением, углами и расстояниями.

Векторы: понимание понятия и их роль в физике

Вектор — это математический объект, который имеет как величину (длину), так и направление. Векторы широко используются в физике для описания физических величин, таких как сила, скорость, ускорение и т. д. Векторы характеризуются не только своей численной величиной, но и своим направлением относительно определенной системы координат.

Одна из ключевых характеристик векторов — их способность сонаправленности, то есть нахождения в одном направлении. Векторы считаются сонаправленными, если у них совпадают направления. Это означает, что они движутся в одном направлении или действуют в одном направлении.

Сонаправленные векторы играют важную роль в физике. Они позволяют суммировать силы, скорости и другие векторы, чтобы получить общий результат. Например, если два вектора имеют одинаковое направление и одинаковую величину, их сумма будет равна двум исходным векторам. Если векторы имеют противоположное направление, их сумма будет равна нулю.

Физические законы и принципы, такие как закон сохранения импульса, основаны на понятии сонаправленности векторов. Зная направление и величину векторов, можно определить их эффекты на объекты и процессы в физической системе.

Для наглядного представления сонаправленных векторов часто используются графические методы, такие как стрелочные диаграммы. На таких диаграммах векторы изображаются стрелками, где длина стрелки обозначает величину вектора, а направление стрелки — его направление.

Изучение сонаправленных векторов позволяет увидеть взаимосвязь различных физических явлений и является важным инструментом для понимания и описания многих физических процессов.

Ссылки[править | править код]

• . — Первое русскоязычное печатное издание по программам, производителям и продавцам САПР. Издается с 2005 г. На сайте издания представлена первая в рунете база данных по теме издания. Дата обращения: 5 мая 2012.
• . — Содержит термины, понятия и аббревиатуры, используемые в отрасли автоматизации проектирования, управления жизненным циклом продукта (PLM) и смежных с ними дисциплинах. Энциклопедия поддерживается порталом isicad. Дата обращения: 27 февраля 2013.
• . — CAD-портал под редакцией Виктора Ткаченко, статьи, программы, документация, новости, обзоры. Дата обращения: 27 февраля 2013.
• Криволинейные поверхности в CAD, учебный фильм

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Конспект урока «Углы с сонаправленными сторонами»

· введем понятие сонаправленных лучей;

· дадим определение сонаправленных лучей;

· докажем теорему о равенстве углов с сонаправленными сторонами.

На этом уроке нам понадобится одна из аксиом планиметрии, которая звучит следующим образом: «любая прямая разбивает плоскость на две полуплоскости».

Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.

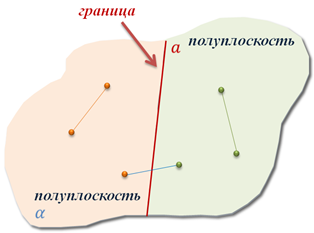
Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.

Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой

Определение. Два луча ОА и О₁А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО₁.

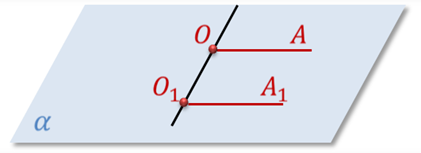
Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.

Лучи ОА и O₁A₁, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.

Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Доказательство. Рассмотрим случай, когда углы О и О₁ с соответственно сонаправленными сторонами лежат в разных плоскостях.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОB и

О₁B₁. Т.е. мы имеем два угла АОB и А₁О₁B₁, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А₁О₁B₁.

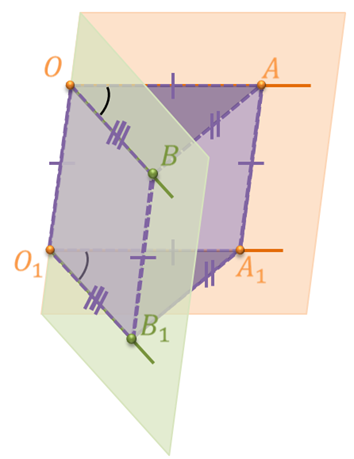
Отметим на сторонах лучей ОА и O₁A₁ точки А и A₁ так, чтобы отрезки ОА и O₁A₁ были равны. На сторонах лучей ОB и O₁B₁ отметим точки B и B₁ так, чтобы отрезки ОB и O₁B₁ были равны.

Рассмотрим четырехугольник ОАA₁O₁. Так как лучи ОА и O₁A₁ параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА₁О₁ является параллелограммом по признаку параллелограмма. Следовательно, АА₁ параллельно ОО₁ и АА₁ равно ОО₁.

Рассмотрим четырехугольник ОBB₁O₁. Его стороны ОB и O₁B₁ параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB₁O₁ является параллелограммом. Тогда, стороны BB₁ и OO₁ параллельны и равны.

Обратите внимание, мы получили, что прямая AA1 параллельна прямой OO1 и прямая BB1 параллельна прямой OO1. Тогда по признаку параллельности прямых в пространстве, прямые AA1 и BB1 параллельны

Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA₁ и BB₁ параллельны и равны. А значит, BAA₁B₁ – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A₁B₁ тоже параллельны и равны.

Теперь рассмотрим треугольники АОB и A₁O₁B₁. Стороны ОА и O₁A₁ равны по построению. Стороны ОB и O₁B₁ также равны по построению. Выше мы доказали, что стороны АB и A₁B₁ равны. Значит, треугольники АОB и A₁O₁B₁ равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A₁O₁B₁ равны. Теорема доказана.

Задание. Рассмотрите рисунок и

а) укажите лучи, которые являются сонаправленными;

б) укажите лучи, которые не являются сонаправленными.

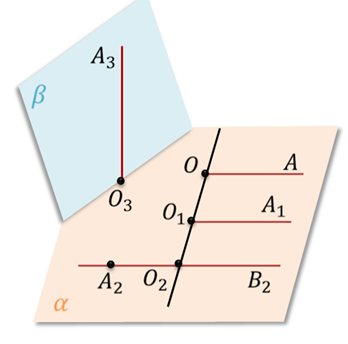
Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.

Источник

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Конспект урока «Углы с сонаправленными сторонами»

· введем понятие сонаправленных лучей;

· дадим определение сонаправленных лучей;

· докажем теорему о равенстве углов с сонаправленными сторонами.

На этом уроке нам понадобится одна из аксиом планиметрии, которая звучит следующим образом: «любая прямая разбивает плоскость на две полуплоскости».

Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.

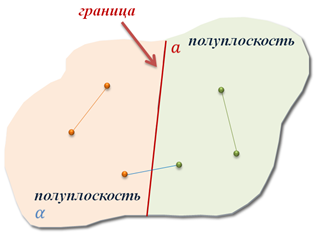
Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.

Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой. Определение

Два луча ОА и О1А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО1

Определение. Два луча ОА и О₁А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО₁.

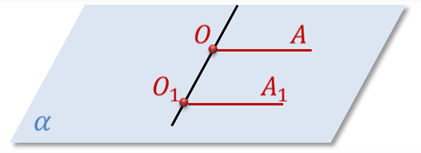
Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.

Лучи ОА и O₁A₁, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.

Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Доказательство. Рассмотрим случай, когда углы О и О₁ с соответственно сонаправленными сторонами лежат в разных плоскостях.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОB и

О₁B₁. Т.е. мы имеем два угла АОB и А₁О₁B₁, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А₁О₁B₁.

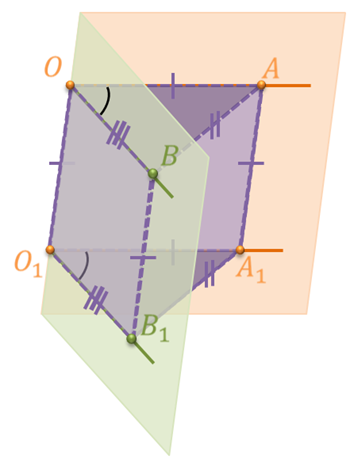
Отметим на сторонах лучей ОА и O₁A₁ точки А и A₁ так, чтобы отрезки ОА и O₁A₁ были равны. На сторонах лучей ОB и O₁B₁ отметим точки B и B₁ так, чтобы отрезки ОB и O₁B₁ были равны.

Рассмотрим четырехугольник ОАA₁O₁. Так как лучи ОА и O₁A₁ параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА₁О₁ является параллелограммом по признаку параллелограмма. Следовательно, АА₁ параллельно ОО₁ и АА₁ равно ОО₁.

Рассмотрим четырехугольник ОBB₁O₁. Его стороны ОB и O₁B₁ параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB₁O₁ является параллелограммом. Тогда, стороны BB₁ и OO₁ параллельны и равны.

Обратите внимание, мы получили, что прямая AA1 параллельна прямой OO1 и прямая BB1 параллельна прямой OO1. Тогда по признаку параллельности прямых в пространстве, прямые AA1 и BB1 параллельны. Рассмотрим четырехугольник BAA1B1

В этом четырехугольнике стороны AA1 и BB1 параллельны и равны. А значит, BAA1B1 – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A1B1 тоже параллельны и равны

Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA₁ и BB₁ параллельны и равны. А значит, BAA₁B₁ – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A₁B₁ тоже параллельны и равны.

Теперь рассмотрим треугольники АОB и A₁O₁B₁. Стороны ОА и O₁A₁ равны по построению. Стороны ОB и O₁B₁ также равны по построению. Выше мы доказали, что стороны АB и A₁B₁ равны. Значит, треугольники АОB и A₁O₁B₁ равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A₁O₁B₁ равны. Теорема доказана.

Задание. Рассмотрите рисунок и

а) укажите лучи, которые являются сонаправленными;

б) укажите лучи, которые не являются сонаправленными.

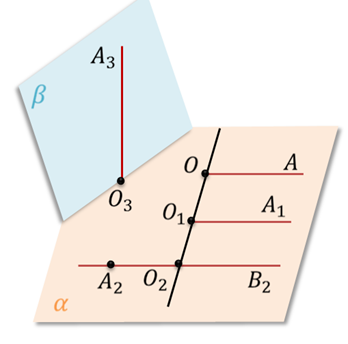
Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.

Источник

Проявления соответственной сонаправленности в различных областях

В физике и механике соответственная сонаправленность может быть проиллюстрирована на примере движения объектов в одном направлении. Например, движение двух автомобилей, двигающихся в одной полосе по дороге, можно считать соответственно сонаправленным. Или движение двух воздушных шаров, летящих в одной стороне.

В электротехнике примером соответственной сонаправленности может служить параллельное соединение электрических резисторов. Когда несколько резисторов соединены параллельно, ток в каждом из них будет течь в одном направлении.

В биологии соответственная сонаправленность может быть наблюдаема в случае одновременного движения множества организмов в одном направлении. Например, стадо животных, двигающихся вместе по полю, можно считать соответственно сонаправленным.

Это лишь некоторые примеры проявления соответственной сонаправленности в различных областях. В целом, это понятие является важным для понимания взаимодействия объектов и процессов, происходящих в различных системах.

Задачи на умножение сонаправленных векторов на число для 9 класса

Вот несколько задач, в которых нужно умножать сонаправленные векторы на число:

1. Вектор AB имеет длину 5 см и направлен вправо. Найдите вектор BC, если он получается путем умножения вектора AB на число 3.
2. Вектор PQ имеет длину 10 м и направлен вверх. Найдите вектор QR, если он получается путем умножения вектора PQ на число 2.
3. Вектор XY имеет длину 15 км и направлен вниз. Найдите вектор YZ, если он получается путем умножения вектора XY на число 4.

Для решения этих задач нужно умножить длину исходного вектора на заданное число, не меняя его направления. В результате получим новый вектор, который и будет искомым.

Используя умножение сонаправленных векторов на число, можно решать различные задачи, связанные с изменением длины вектора. Это огромное применение находит в реальной жизни, например, в физике, строительстве и навигации.

Определение сонаправленных векторов

Для определения сонаправленных векторов необходимо учитывать следующее:

• Векторы должны быть ненулевыми, то есть они должны иметь ненулевую длину.
• Длины векторов могут отличаться, но это не влияет на их сонаправленность. Главное, чтобы они указывали в одном направлении.
• Векторы могут быть параллельными или антипараллельными. Параллельные векторы сонаправлены, тогда как антипараллельные имеют противоположное направление, но также сонаправлены.

Сонаправленные векторы можно представить графически, например, стрелками, указывающими в одном направлении. Векторы могут иметь как положительное, так и отрицательное направление в зависимости от выбранной системы координат.

Примером сонаправленных векторов может служить движение автомобилей по одной и той же дороге в одном направлении. Векторы скорости этих автомобилей будут сонаправленными, так как они указывают в одном направлении — вперед.

Значение сонаправленных векторов в физике и математике

Сонаправленные векторы являются важным понятием как в физике, так и в математике. Они играют важную роль в решении различных задач и формулировке законов природы. Вот несколько основных областей, в которых сонаправленные векторы имеют большое значение.

Физика

В физике, сонаправленные векторы используются для описания движения тел и взаимодействия сил. Вектор скорости, например, является сонаправленным вектором, который показывает направление и скорость движения тела. Сонаправленные векторы также используются для описания сил и моментов, вызывающих вращение тел.

Математика

В математике, сонаправленные векторы используются для решения геометрических задач. Они могут быть использованы для определения расстояния между точками и вычисления площади и объема фигур. Сонаправленные векторы также используются для решения систем линейных уравнений и нахождения решений дифференциальных уравнений.

Применение в технических науках

Сонаправленные векторы имеют широкое применение в технических науках, таких как инженерия и компьютерная графика. Они используются для моделирования и визуализации объектов, прогнозирования поведения систем, разработки алгоритмов и решения задач оптимизации.

В заключение, сонаправленные векторы играют важную роль в физике и математике, обеспечивая нам средство для описания и анализа различных явлений и задач. Они помогают нам понять и предсказывать поведение объектов и систем, а также находить способы их оптимизации и решения.

Что такое координаты вектора

Вектором называют некое направление в виде отрезка с определенными в пространстве начальной и конечной точками.

Предусмотрено стандартизированное обозначение вектора. К примеру, если в точке А какой-то вектор берет свое начало, а в точке В — заканчивается, то его записывают таким образом: \(\overrightarrow{AB}\).  Допустимо использовать и сокращенный вариант, к примеру: \(\overrightarrow{a}\).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. В некоторых случаях уместно сформулировать понятие вектора как передвижение из начальной точки А в конечную точку В

Согласно ранее записанному определению, вектор характеризуется некой длиной. К примеру, для \(\overrightarrow{AB}\) длиной, либо модулем, является протяженность отрезка АВ. Данное утверждение допустимо сформулировать в виде математического соотношения:

В некоторых случаях уместно сформулировать понятие вектора как передвижение из начальной точки А в конечную точку В. Согласно ранее записанному определению, вектор характеризуется некой длиной. К примеру, для \(\overrightarrow{AB}\) длиной, либо модулем, является протяженность отрезка АВ. Данное утверждение допустимо сформулировать в виде математического соотношения:

\(|\overrightarrow{AB}|=AB\)

Примечание 1

Заметим, что не исключены случаи совпадения начальной и конечной точек рассматриваемого вектора. Тогда говорят, что этот вектор является нулевым.

Школьникам и студентам часто приходится иметь дело с векторами. С таким понятием нередко встречаются учащиеся в процессе решения контрольных и самостоятельных работ по геометрии и физике. Как правило, рассматривается декартова координатная система, ориентируясь на которую можно вычислить координаты соответствующего отрезка с конкретным направлением. Процедура заключается в разложении заданного направленного отрезка по базисным векторам.

Принцип основан на фундаментальных знаниях геометрии. В результате получается интерпретировать это действие в виде векторной проекции относительно осей координат. При наличии данных о координатах, которым соответствуют точки начала и конца вектора, представляется возможным рассчитать непосредственно координаты искомого вектора. Процедура подразумевает расчет разности между координатами точки, где вектор заканчивается, и координатами точки, в которой он начинается.

Рассматриваемое действие по идентификации координат вектора целесообразно записать в общей форме таким образом:

\(\overrightarrow {AB}=(AB_{x},AB_{y},AB_{z})=(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z})\)

В качестве базиса принято рассматривать орты координат. Для их обозначения используют \({\vec {k}}{\vec {i}},{\vec {j}},{\vec {k}}\), которые соответствуют осям x,y,z. При таких условиях \({\vec {a}}\) допустимо выразить с помощью следующего математического соотношения:

\({\vec {a}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}+a_{z}{\vec {k}}\)

Заметим, что какое-либо свойство в науке геометрии допустимо сформулировать с помощью координат. В результате оно приобретает алгебраическую форму, что позволяет значительно упростить решение тех или иных задач. С другой стороны, несколько некорректно применять обратный принцип действий.

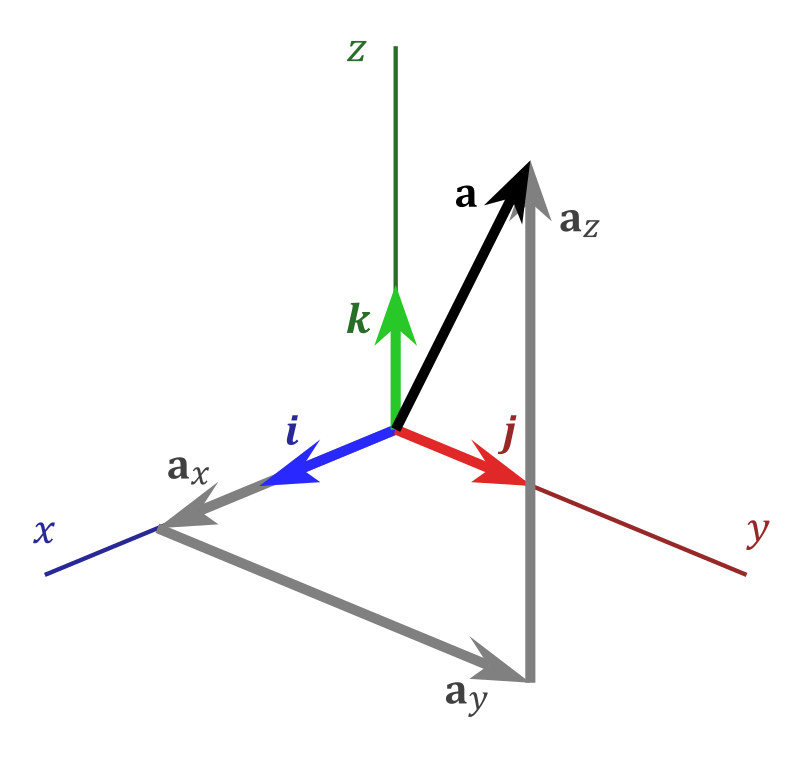
Координаты вектора представляют собой проекции х и у заданного вектора \(\overrightarrow {AB}\) на координатные оси в рамках прямоугольной координатной системы.

В решении задач уже привычно использовать различные закономерности, с помощью которых можно значительно упростить вычисления. В ходе изучения темы координат вектора можно также выделить несколько полезных признаков. Перечислим свойства направленных отрезков:

1. В рамках общей координатной системы какие-либо векторы, которые идентичны друг другу, обладают аналогичными координатами.
2. Если вектора являются коллинеарными, то их координаты пропорциональны. При этом рассматриваемые вектора не должны обладать нулевым значением.
3. Протяженность произвольного вектора во второй степени соответствует результату сложения координат данного вектора, возведенных во вторую степень.
4. Произведение некого вектора и числа из множества действительных подразумевает произведение каждой из координат заданного вектора на это число.
5. Если требуется суммировать вектора, то следует сложить их координаты.
6. Вычисление скалярного произведения пары векторов заключается в сложении произведений координат, которые принадлежат рассматриваемым векторам.

Примеры вычисления косинуса угла между двумя векторами

Вычисление косинуса угла между двумя векторами является одним из ключевых понятий линейной алгебры. Для его определения необходимо знание скалярного произведения векторов.

Пусть имеются два вектора A и B в трехмерном пространстве. Для вычисления косинуса угла между ними достаточно разделить скалярное произведение на произведение модулей векторов:

cos α = (A · B) / (|A| * |B|)

Для наглядности можно привести пример с координатами: если A(2,3,4) и B(5,6,7), то:

cos α = ((2*5) + (3*6) + (4+7)) / (√(2²+3²+4²) * √(5²+6²+7²)) = 0.994

Таким образом, косинус угла между этими векторами составляет 0.994, что означает, что они сонаправлены.

Если же косинус угла равен 0, то векторы ортогональны (то есть перпендикулярны друг другу), а если косинус угла меньше 0, то они направлены в противоположных направлениях.

Типы классов разрядов и их функции

1. Десятичные разряды

Десятичные разряды — это типы классов разрядов, используемые в десятичной системе счисления. В каждом десятичном числе присутствуют следующие разряды: единицы, десятки, сотни, тысячи и т.д. Каждый разряд указывает на количество определенных единиц, которые входят в число.

2. Двоичные разряды

Двоичные разряды — это типы классов разрядов, используемые в двоичной системе счисления. В двоичных числах присутствуют следующие разряды: единицы, двойки, четверки, восьмерки и т.д. Каждый разряд указывает на количество определенных единиц, которые входят в число.

3. Восьмеричные разряды

Восьмеричные разряды — это типы классов разрядов, используемые в восьмеричной системе счисления. В восьмеричных числах присутствуют следующие разряды: единицы, восьмерки, шестнадцатерки и т.д. Каждый разряд указывает на количество определенных единиц, которые входят в число.

4. Шестнадцатеричные разряды

Шестнадцатеричные разряды — это типы классов разрядов, используемые в шестнадцатеричной системе счисления. В шестнадцатеричных числах присутствуют следующие разряды: единицы, шестерки, шестнадцатерки и т.д. Каждый разряд указывает на количество определенных единиц, которые входят в число.

Таблица ниже иллюстрирует структуру и функции различных классов разрядов:

• Десятичные разряды:
  • Единицы: указывает на количество единиц в числе.
  • Десятки: указывает на количество десятков в числе.
  • Сотни: указывает на количество сотен в числе.
  • Тысячи: указывает на количество тысяч в числе.
• Двоичные разряды:
  • Единицы: указывает на количество единиц в числе.
  • Двойки: указывает на количество двоек в числе.
  • Четверки: указывает на количество четверок в числе.
  • Восьмерки: указывает на количество восьмерок в числе.
• Восьмеричные разряды:
  • Единицы: указывает на количество единиц в числе.
  • Восьмерки: указывает на количество восьмерок в числе.
  • Шестнадцатерки: указывает на количество шестнадцатерок в числе.
• Шестнадцатеричные разряды:
  • Единицы: указывает на количество единиц в числе.
  • Шестерки: указывает на количество шестерок в числе.
  • Шестнадцатерки: указывает на количество шестнадцатерок в числе.

Каждый из типов разрядов имеет свои особенности и применяется в различных областях. Понимание функций и структуры классов разрядов поможет лучше понять и использовать числа в различных системах счисления.

Примеры в геометрии и приложениях

Сонаправленные вектора находят широкое применение в геометрии и других приложениях. Вот несколько примеров:

1. Векторные операции:

Сонаправленные вектора используются во многих векторных операциях, таких как сложение, вычитание и умножение векторов на скаляр. Например, при сложении двух сонаправленных векторов их значением будет вектор с той же направленностью и суммой их длин.

2. Соотношение между векторами и их компонентами:

Сонаправленные вектора позволяют установить соотношение между векторами и их компонентами. Например, если имеется вектор сонаправленный оси координат, его компоненты относятся к основным направлениям соответствующих осей.

3. Вычисление проекций:

Сонаправленные вектора широко используются для вычисления проекций векторов на плоскости или на оси. Например, при проецировании вектора на плоскость, проекции будут иметь одинаковое направление.

4. Расчет сил и скоростей:

В физике сонаправленные вектора применяются для расчета сил и скоростей. Например, сила, направленная вдоль оси, может быть представлена как сонаправленный вектор, а его величина будет определять величину силы.

5. Анализ направления и углов:

Сонаправленные вектора используются для анализа направления и углов между ними. Например, можно определить угол между двумя сонаправленными векторами, используя угловую функцию их компонент.

Все эти примеры показывают, что понимание и работы с сонаправленными векторами является важной частью геометрии и имеет широкий спектр приложений

Литература[править | править код]

• Латышев П.Н. Каталог САПР. Программы и производители: Каталожное издание. — М.: ИД СОЛОН-ПРЕСС, 2006, 2008, 2011. — 608, 702, 736 с. — ISBN 5-98003-276-2, 978-5-91359-032-9, 978-5-91359-101-2.
• Малюх В. Н. Введение в современные САПР: Курс лекций. — М.: ДМК Пресс, 2010. — 192 с. — ISBN 978-5-94074-551-8.
• Муромцев Ю. Л., Муромцев Д. Ю., Тюрин И. В. и др. Информационные технологии в проектировании радиоэлектронных средств: учеб. пособие для студ. высш. учебн. заведений. — М.: Издательский центр «Академия», 2010. — 384 с. — ISBN 978-5-7695-6256-3.
• Норенков И. П. Основы автоматизированного проектирования: учеб. для вузов. — 4-е изд., перераб. и доп. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2009. — 430 с. — ISBN 978-5-7038-3275-2.
• Морозов К. К., Одиноков В. Г., Курейчик В. М. Автоматизированное проектирование конструкций радиоэлектронной аппаратуры. — М.: Радио и связь, 1983. — 280 с. — (Учебное пособие для вузов).

3.1 Понятие atomic вектора в R

Если у вас не было линейной алгебры (или у вас с ней было все плохо), то просто запомните, что вектор (atomic vector или просто atomic) – это набор (столбик) чисел в определенном порядке.

Если вы привыкли из школьного курса физики считать вектора стрелочками, то не спешите возмущаться и паниковать. Представьте стрелочки как точки из нуля координат {0,0} до какой-то точки на координатной плоскости, например, {2,3}:

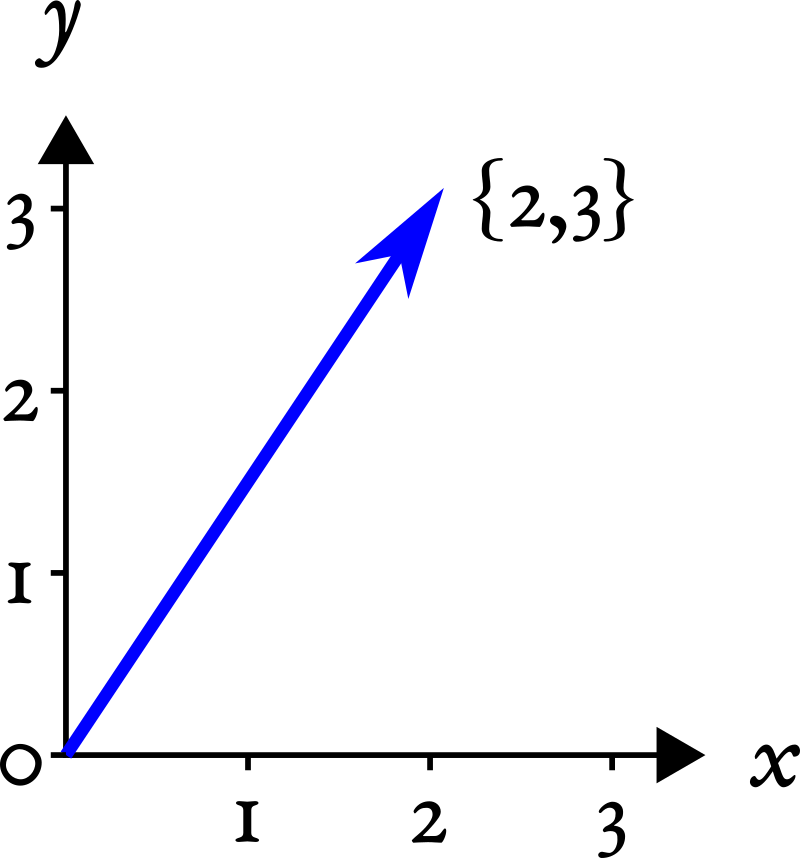
Вот последние два числа и будем считать вектором. Попытайтесь теперь мысленно стереть координатную плоскость и выбросить стрелочки из головы, оставив только последовательность чисел {2,3}:

На самом деле, мы уже работали с векторами в R, но, возможно, вы об этом даже не догадывались. Дело в том, что в R нет как таковых скалярных (т.е. одиночных) значений, есть вектора длиной 1. Такие дела!

Чтобы создать вектор из нескольких значений, нужно воспользоваться функцией :

Осторожно: ошибка с кириллической “с”

Одна из самых мерзких и раздражающих причин ошибок в коде – это использование из кириллицы вместо из латиницы. Видите разницу? И я не вижу. А R видит. И об этом сообщает:

Для создания числовых векторов есть удобный оператор .

Этот оператор создает вектор от первого числа до второго с шагом 1. Вы не представляете, как часто эта штука нам пригодится… Если же нужно сделать вектор с другим шагом, то есть функция :

Кроме того, можно задавать не шаг, а длину вектора. Тогда функция сама посчитает шаг:

Другая функция – – позволяет создавать вектора с повторяющимися значениями. Первый аргумент – значение, которое нужно повторять, а второй аргумент – сколько раз повторять.

И первый, и второй аргумент могут быть векторами! Если второй агрумент – вектор такой же длины, то каждое значение первого вектора будет повторено соответствующее количество раз из второго вектора.

Если нужно повторить каждое значение в векторе одно и то же количество раз, то можно воспользоваться дополнительным параметром :

Еще можно объединять вектора (что мы, по сути, и делали, просто с векторами длиной 1):

Очень многие функции в R работают именно с векторами. Например, функции (считает сумму значений вектора) и (считает среднее арифметическое всех значений в векторе):

Понятие скрещивающихся прямых

В пространстве можно построить две прямые так, что они не будут пересекаться, но и параллельными они также являться не будут. Для этого достаточно, чтобы прямые НЕ находились в одной плоскости. В этом случае их именуют скрещивающимися прямыми.

Здесь ребра ВС и АЕ как раз лежат на двух скрещивающихся прямых. Поэтому их можно так и называют – скрещивающиеся отрезки. По аналогии можно ввести понятие и скрещивающихся лучей.

Существует теорема, представляющая собой признак скрещивающихся прямых.

Действительно, пусть есть две прямые, НК и РМ. Обозначим как α плос-ть, проходящую через НК и точку М. Если РМ пересекает α, то это означает, что М – единственная общая точка у α и РМ. Получается, что Н, К, М и Р – это точки в различных плос-тях, и через них нельзя провести одну плос-ть. Значит, и прямые НК и РМ – скрещивающиеся.

Таким образом, в стереометрии возможно всего три случая взаимного расположения двух прямых в пространстве:

1) прямые пересекаются, и тогда они обязательно находятся в одной плос-ти;

2) прямые располагаются в одной плос-ти, но не пересекаются – случай параллельных прямых;

3) прямые находятся в разных плос-тях – случай скрещивающихся прямых.

Докажем одну теорему:

Для доказательства возьмем произвольные скрещивающиеся прямые m и n. Отметим на n точку К и проведем через К прямую р, параллельную m:

Через пересекающиеся прямые nи p можно провести единственную плос-тьα. По признаку параллельности прямой и плос-ти можно заключить, что m||α.

Покажем, что кроме α нет других плос-тей, проходящих через n и параллельных m. Действительно, если бы такая плос-ть β существовала, то р имела бы с ней общую точку К, но полностью в β она бы не могла находиться, иначе α и β совпадали бы. Значит, р пересекала бы β. Но тогда ее обязательно пересекала бы и m по одну из свойств параллельных прямых. В этом случае m и β не были бы параллельными.