Задачи на 1 закон Ньютона
Прежде чем рассмотреть решение задач на первый ньютоновский закон, вспомним теорию.
Формулировка
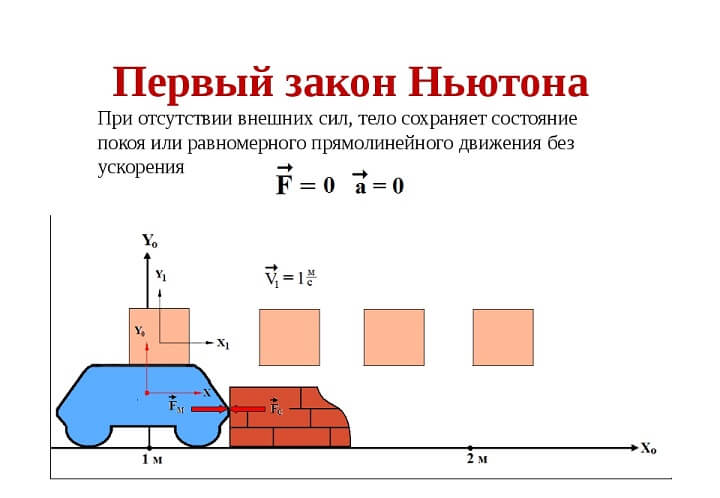
В инерциальных системах отсчета тело неподвижно или двигается равномерно и прямолинейно при условии, что на него нет воздействия других сил или их действие компенсируется. По-другому эту закономерность называют законом инерции.
Если говорить простым языком, то первый закон Ньютона означает, что тело, если оно находится в покое, будет неподвижным до тех пор, пока на него не окажет воздействие какая-либо сила. Примером может служить мяч, неподвижно лежащий на газоне. Мяч будет оставаться в покое до тех пор, пока по нему не ударят, заставив двигаться. То же самое относится и ко второй части формулировки первого ньютоновского закона: тело, движущееся равномерно и прямолинейно, будет так двигаться до тех пор, пока не получит воздействие какой-либо силы.
Примером является парашютист, летящий к поверхности земли. Пока притяжение к Земле и сопротивление воздуха будут компенсировать друг друга, парашютист будет двигаться прямолинейно и равномерно. Как только одна из сил станет больше, а вторая меньше, движение парашютиста станет прямолинейным и равноускоренным.
Примеры задач и решения
Так как для первого закона Ньютона нет формулы, задачи представляют собой теоретические размышления.
Задача 1
В каких из приведенных ниже случаев систему отсчета можно считать инерциальной:
Решение:
Согласно первому ньютоновскому закону, в инерциальных системах объект или находится в состоянии покоя, или движется прямолинейно и равномерно. Из приведенных вариантов подходит второй вариант.
Задача 2
Если на тело не действуют другие тела или действуют, но сумма их воздействия равна нулю, то тело:
Решение:
Согласно первому закону Ньютона, верным будет последний вариант.
Закон сохранения импульса
Закон сохранения импульса
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:
Замкнутая система – это система, на которую не действуют внешние силы.Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций.
При абсолютно упругом ударе взаимодействующие тела до и после взаимодействия движутся отдельно.
Закон сохранения импульса для абсолютно упругого удара:
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Закон сохранения импульса для абсолютно неупругого удара:
Реактивное движение – это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-то его части.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой, поэтому реактивное движение позволяет телу двигаться в безвоздушном пространстве.
Реактивные двигатели
Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Используются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-ракетными двигателями.
Реактивные двигатели делятся на два класса:
- ракетные;
- воздушно-реактивные.
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.
Ракетный двигатель на твердом топливе
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где находится сопло. Выходящие через сопло газы не встречают на своем пути стенку, на которую могли бы оказать давление. В результате появляется сила, толкающая ракету вперед.
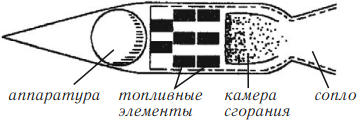
Сопло – суженная часть камеры, служит для увеличения скорости истечения продуктов сгорания, что, в свою очередь, повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.
Ракетный двигатель на жидком топливе
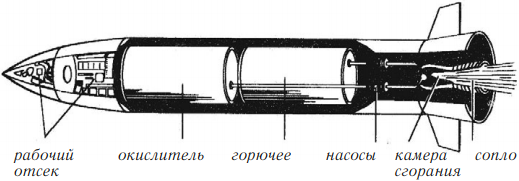
В ракетных двигателях на жидком топливе в качестве горючего используют керосин, бензин, спирт, жидкий водород и др., а в качестве окислителя – азотную кислоту, жидкий кислород, перекись водорода и пр.
Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру сгорания, где температура достигает 3000 0С и давление до 50 атм. В остальном работает так же, как и двигатель на твердом топливе.
Воздушно-реактивный двигатель
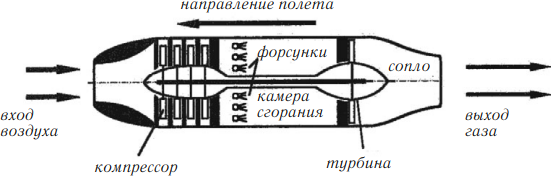
В носовой части находится компрессор, засасывающий и сжижающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (керосин) попадает в камеру сгорания с помощью специальных форсунок. Раскаленные газы выходят через сопло, вращают газовую турбину, приводящую в движение компрессор.
Основное отличие воздушно-реактивных двигателей от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы.
Алгоритм применения закона сохранения импульса к решению задач:
- Запишите краткое условие задачи.
- Определите характер движения и взаимодействия тел.
- Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
- Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
- Запишите закон сохранения импульса в векторной форме.
- Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
- Решите полученную систему уравнений относительно неизвестных величин.
- Выполните действия единицами измерения величин.
- Запишите ответ.
Второй закон Ньютона
В примере с автобусом вы видите, что пассажиры пытаются сохранить свою скорость относительно Земли, инерциальной системы отсчета. Это явление называется инерцией. Инерция — это явление, благодаря которому тело сохраняет состояние покоя или равномерного прямолинейного движения. Инерция — это физическое свойство, согласно которому любое тело сопротивляется изменению своей скорости (как по степени, так и по направлению). Не все тела одинаково инертны. Вы можете взять мяч и придать ему большое ускорение. Но вы не можете придать гире такое же ускорение, даже если она схожа по размеру. Однако мяч и гиря различаются по массе. Масса — это масштабируемая физическая величина, которая является мерой инерции тела. Чем больше масса, тем больше инерция тела. Масса обозначается буквой m. Единицей измерения массы является кг. Одним из инструментов для измерения массы являются весы. Чтобы придать двум телам с разной инерцией одинаковую скорость, необходимо приложить большую силу к телу с большей инерцией. Попробуйте передвинуть стол, а затем шкаф. Стол будет легче перемещать. Если приложить одинаковую силу к телу с разной инерцией, то можно обнаружить, что тело с меньшей инерцией испытает большее ускорение. Если положить теннисный мяч на пружину, сжать ее и резко отпустить, мяч улетит. Если вы возьмете железный мяч вместо теннисного, он прокатится только на определенное расстояние. Описанные выше примеры показывают, что существует взаимосвязь между силой, приложенной к телу, и ускорением, которое оно испытывает в результате приложения силы, и массой тела. Это видно из второго закона движения Ньютона. Второй закон Ньютона Сила, действующая на тело, равна произведению массы тела на ускорение, вызванное силой. F = ma, где F — сила, действующая на тело, a — ускорение, вызванное этой силой, m — масса тела Сила — это количественная мера действия тел друг на друга, в результате которого тела испытывают ускорения. Сила — это векторная физическая величина. Он обозначается как F. Единицей измерения является Н (Ньютон). Инструментом для измерения силы является динамометр. Пример 1. Определите силу, с которой Земля действует на яблоко, когда оно падает с ветки, а ускорение яблока равно 9,8 м/с2. Масса яблока равна 200 г. Переведите массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, с которой Земля действует на яблоко в соответствии со вторым законом движения Ньютона.
Иногда на одно тело действует много сил. В этом случае в описание движения вводится понятие конституирующей силы. Определение Эквивалентная сила — это векторная сумма всех сил, одновременно действующих на тело. R = F1+ F2+ F3+ … В этом случае второй закон Ньютона формулируется следующим образом: Второй закон движения Ньютона обусловлен составляющими силами Если на тело действует множество сил, то их составляющая R равна произведению массы на ускорение тела. m a = R = F1+ F2+ F3+ …
Правила сложения сил и их проекций
| Сложение двух сил, направленных вдоль прямой линии в одном направлении | |
| Если F1↑↑ F2тогда: R = F1+ F2Результирующая сила является обратной величиной двух сил. | |
| Сложение двух сил, действующих вдоль прямой линии в противоположных направлениях. | |
| Если F1↑↓ F2тогда: R = | F1– F2| Результирующая сила направлена в сторону большей силы. | |
| Сложение двух сил, которые перпендикулярны друг другу | |
| Если F1перпендикулярна F2то результирующая сила вычисляется по теореме Пифагора: | |
| Сложение двух сил, расположенных под углом a друг к другу | |
| Если F1и F2образуют между собой угол a, результирующая сила рассчитывается по теореме косинусов: | |
| Сложение трех сил | |
| Способ сложения определяется правилами сложения векторов. В данном случае: | |
| Добавление проекций силы | |
| Проекция на ось OX: F1x+ F2x– F3x= 0 Проекция на ось OY: F1y– F2y= 0 |
Ошибки и заблуждения, связанные с понятием центробежная сила[править | править код]
Отсутствие единой общепризнанной терминологии в учебниках и научной литературе по физике и механике, касающейся центробежных сил инерции, приводит к путанице понятий, ошибкам, парадоксам, а иногда и к полному непониманию сути изучаемого вопроса. Один из примеров такого рода описан в Общем курсе физики Д. В. Сивухина. Автор пишет:
«Центробежные силы, как и всякие силы инерции, существуют лишь в ускоренно движущихся (вращающихся) системах отсчёта и исчезают при переходе к инерциальным системам. Забыв это, можно прийти к парадоксам, которые часто ставят в тупик школьников. Вот один из самых распространённых парадоксов такого типа. Пусть тело движется по окружности. На него действуют две силы: центростремительная F→1{\displaystyle {\vec {F}}_{1}}, направленная к центру окружности, и центробежная F→2{\displaystyle {\vec {F}}_{2}}, направленная в противоположную сторону. Эти силы равны по модулю и уравновешивают друг друга. F→1+F→2={\displaystyle {\vec {F}}_{1}+{\vec {F}}_{2}=0.} По закону инерции тело должно двигаться прямолинейно и равномерно.
Противоречие возникло потому, что движение стали относить к неподвижной (инерциальной) системе отсчёта. А в этой системе никаких центробежных сил не существует. Есть только одна центростремительная сила F→1{\displaystyle {\vec {F}}_{1}}, которая и сообщает телу ускорение.
Путаница происходит из-за того, что в технической механике термин центробежная сила иногда употребляют в совершенно другом смысле. Центробежной силой называют силу реакции с которой тело A, вращающееся по окружности, действует на тело B, принуждающее его совершать это вращение. Равную и противоположно направленную силу, с которой тело B действует на вращающееся тело A, называют центростремительной…. Центростремительная и центробежная силы, так понимаемые, всегда приложены к разным телам…».
Однако, понимая центробежную силу в этом смысле, которая в учебнике Фриш и Тиморевой названа «действительной» центробежной силой, и считать, что она удаляет вращающееся тело от центра, совершенно абсурдно, поскольку эта сила к телу не приложена.
Единственно, в чём можно «упрекнуть» Сивухина, это то, что указанный им парадокс относится лишь к незадачливым школьникам. Такое же «понимание» центробежных и центростремительных сил нередко встречается у студентов, аспирантов, инженеров и даже у преподавателей физики.
Вот пример из широко распространённой в США книги Л. Эллиот и У. Уилкокса «Физика», которая вышла в переводе на русский язык под ред. А. И. Китайгородского в 1975 году.
В главе 17 этой книги рассматривается простейший случай равномерного движения по окружности шарика, привязанного к верёвке. К шарику приложены четыре силы: F→1{\displaystyle {\vec {F}}_{1}} — движущая сила, направленная по касательной к окружности и, равная ей по величине, но противоположно направленная, сила инерции F→2,{\displaystyle {\vec {F}}_{2},} а также сила F→4{\displaystyle {\vec {F}}_{4}}, направленная к центру окружности и, равная ей по величине, сила F→3{\displaystyle {\vec {F}}_{3}}, направленная в противоположную сторону (от центра).
Далее, по тексту:
«Сила F→4{\displaystyle {\vec {F}}_{4}}, тянущая тело к центру и сворачивающая тело с прямолинейного пути, называется центростремительной силой. Но центростремительная сила — это не единственная сила, действующая во время движения по окружности, потому что, согласно третьему закону Ньютона, силы всегда действуют парами. Если существует центростремительная сила, то должна быть и другая сила F→3{\displaystyle {\vec {F}}_{3}}, равная ей по величине, но противоположная по направлению. Эта сила называется центробежной силой…»
Казалось бы, исходя из написанного, речь идёт об инерциальной системе и центробежной силе в её первом значении, согласно БСЭ. Но, в следующем абзаце читаем:
«Действие центробежной силы ощущают на себе пассажиры, едущие в автобусе или автомобиле, когда машина делает крутой поворот.»
Стало быть речь идёт о неинерциальной системе отсчёта и уже о центробежной силе инерции во втором её значении, а это как раз тот же самый, описанный Сивухиным случай путаницы и неразберихи, но уже не в голове школьника, а в учебной литературе.
Из всего сказанного можно сделать вывод: пока не будет разработана единая система терминологии, следует внимательно относиться к выражению центробежная сила и в каждом конкретном случае выяснять, к какому понятию оно относится.
А теперь несколько распространенных мифов:
- Пресловутое яблоко, наверное, известно каждому школьнику. Во время начала эпидемии чумы (1665 год) Ньютон, раздав студентам домашние задания, вынужден был уехать из Кембриджа и остановиться в деревушке, о названии которой история умалчивает. Именно тогда и родилась легенда о яблоке, ведь ученый не переставал работать и удивлял новыми открытиями. Впрочем, биографы Ньютона так и не сошлись во мнениях: был ли такой случай, либо же нет.
- За свои заслуги перед Кембриджским университетом в 1689 году уважаемого ученого избрали членом парламента, что было довольно престижной должностью. При этом, за все время заседаний этого парламента со своим участием Ньютон высказался всего один раз. Он попросил закрыть окно, поскольку было прохладно.
- Неизвестно, откуда пошла эта легенда, но многие считают, что Ньютон изобрел маленькую откидную дверцу во входных дверях, как сейчас делают для кошек. Якобы у него была кошка, и чтобы она не мешала работать, он сделал ей такою дверцу.
- На самом деле Ньютон был посвящен в рыцари вовсе не за научные заслуги, как принято считать. Королева Анна даровала ему рыцарский титул ради поддержки партии вигов, от которых ученый баллотировался в Парламент. Впрочем, он все равно проиграл выборы.
Исаак Ньютон внес неоценимый вклад в науку. Его три главных закона механики стали основой для множества открытий, причем даже через сотни лет, после него. Мы разобрали законы Ньютона кратко и с формулами. Надеемся, вам будет полезна эта информация.
Преимущества скомпенсированного действия сил
Скомпенсированное действие сил представляет собой ситуацию, когда действующие на объект силы имеют равную по модулю силы, но противоположные направления. Такое сбалансированное состояние объекта может иметь несколько преимуществ:
- Устойчивость: Когда действующие на объект силы скомпенсированы, объект остается в равновесии или движется с постоянной скоростью. Это обуславливает устойчивость системы и предотвращает нежелательные внешние воздействия на объект.
- Экономия энергии: В ситуации скомпенсированного действия сил объект тратит минимальное количество энергии на преодоление внешних силовых воздействий. Это позволяет достичь оптимальной энергетической эффективности и сэкономить ресурсы.
- Предсказуемость движения: Скомпенсированное действие сил обеспечивает более предсказуемое движение объекта. В отсутствии неравномерных и несбалансированных сил объект движется по прямой или остается в состоянии покоя.
- Избежание повреждений объекта: Скомпенсированное действие сил также способствует защите объекта от причиняемых нежелательных повреждений. Благодаря равновесию сил объект не подвергается излишнему напряжению, что позволяет предотвратить поломки и повреждения.
В целом, скомпенсированное действие сил является желательным состоянием для объекта, так как обеспечивает его стабильность, энергоэффективность и защищает от нежелательных последствий воздействия внешних сил.
Задачи и вопросы на 2 закон Ньютона
Вопрос 1. Как можно сформулировать второй закон Ньютона, используя понятие «количества движения»?
Ответ. В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на неё силе.
Действительно, импульс (или количество движения) равен произведению массы и скорости. Взяв производную по времени от скорости, мы получим ускорение и придем к классической формулировке второго закона Ньютона: F=ma.
Вопрос 2. Как определяется равнодействующая сила?
Ответ: Равнодействующая сила определяется по правилу сложения векторов. При решении задач бывает удобно рассматривать проекции векторов на определенную ось.
Вопрос 3. Как записать второй закон Ньютона для вращательного движения?
Ответ. Для вращательного движения аналог второго закона Ньютона запишется в виде:
Здесь M – момент силы, J – момент инерции вращающегося тела, эпсилон – угловое ускорение.
Вопрос 4. Что такое сила?
Ответ. Сила – векторная физическая величина, мера взаимодействия тел. Измеряется в Ньютонах. Один Ньютон – такая сила, которая придает телу массой 1 килограмм ускорение равное 1 метр на секунду в квадрате.
Задача №2. Нахождение массы по второму закону Ньютона
Условие
Под действием постоянной силы, равной 10 Н, тело движется прямолинейно. Зависимость координаты тела от времени описывается уравнением х = 3 — 2t + t^2. Какова масса тела?
Решение
Задача сводится к тому, чтобы из закона движения вычислить ускорение, а потом с помощью второго закона Ньютона найти массу.
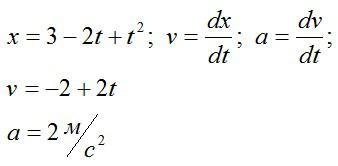
Записываем второй закон Ньютона и подставляем значения:
Ответ: 5 кг.
Задача №3. Нахождение силы по второму закону Ньютона
Условие
Локомотив имеет массу 500 тонн. Через 25 с после того, как он тронулся с места, скорость локомотива стала равна 18 км/ч. Какова сила тяги локомотива?
Решение
Так как начальная скорость равна нулю, ускорение поезда можно найти по формуле:
Записываем второй закон Ньютона и составляем пропорцию, при вычислениях не забывая переводить все данные из условия в систему СИ:
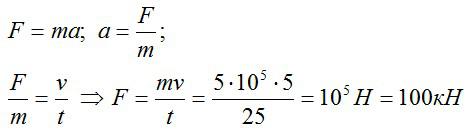
Ответ: 100 кН.
Задача №4. Нахождение ускорения по второму закону Ньютона
Условие
Масса тела равна 500 г. Какое ускорение приобретет тело под действием силы 0,2 Н?
Решение
Для нахождения ускорения достаточно записать второй закон Ньютона, выразить из него ускорение, подставить значения и вычислить:
Ответ: 0,4 метра на секунду в квадрате.
Историческая справка[править | править код]
Понятия силы инерции и центробежная сила впервые упоминаются у Ньютона в его классической книге «Математические начала натуральной философии». Говоря о «врождённой силе материи», то есть о свойстве любого тела сохранять своё состояние покоя или равномерного прямолинейного движения в отсутствии действия каких-либо сил, Ньютон не даёт чёткого определения силы инерции и смешивает понятие инерция — состояние, в котором находится тело, с понятием инертность — свойство тела. Ньютон также использует термин центробежная сила, но рассматривает её как реальную физическую силу, то есть в первом значении, согласно БСЭ. Подобное смешение терминов сохраняется и по сей день.
В 1743 г. д’Аламбер предложил другой подход к силам инерции, в частности, к центробежной силе инерции. Он сформулировал фундаментальный принцип д’Аламбера, суть которого состоит в том, что, для упрощения решения динамической задачи в инерциальной системе отсчёта, к реально действующим силам F→i{\displaystyle {\vec {F}}_{i}} искусственно добавлялись фиктивные силы инерции, равные им по величине, но противоположно направленные F→u=−ma→{\displaystyle {\vec {F}}_{u}=-m{\vec {a}}}, где a→{\displaystyle {\vec {a}}} — ускорение тела. В результате уравнение движения тела принимает вид ∑(F→i+F→u)={\displaystyle \sum ({\vec {F}}_{i}+{\vec {F}}_{u})=0}, и сводится к решению задачи статической.
Пожалуй, ни одно из положений теоретической механики не вызывало столько споров и путаницы, как принцип д’Аламбера. В 20-е годы прошлого века против него выступили философы, обвинявшие автора в недиалектичности, поскольку изучение движения по д’Аламберу сводится к изучению статической задачи — равновесия, которое является частным случаем задачи динамической.
В 1936—1937 годах в советской прессе возникла дискуссия о силах инерции, в частности, о центробежной силе, между инженерами-практиками и механиками-теоретиками по вопросу критики взглядов на инерцию известного советского учёного — механика Л. Б. Левенсона, который писал о том, что практики давно уже ведут расчёты машин, учитывая реальность сил инерции, а теоретики, не считаясь с фактами, настаивают на нереальности сил инерции и утверждают, что эти силы вовсе не существуют.
В 1940 г. вышла книга профессора С. Э. Хайкина «Что такое силы инерции», в которой он выступал с позиций учёных — сторонников реальности инерционных сил.
Известны несколько ожесточённых дискуссий в среде специалистов по механике по поводу того, следует ли считать силы инерции реальными силами или же относить их к воображаемым или фиктивным. Последняя такая дискуссия прошла в Институте проблем механики АН СССР между сторонниками академика А. Ю. Ишлинского (считал, что силы инерции фиктивны) и сторонниками академика Л. И. Седова (считал, что силы инерции реальны) на Всесоюзном совещании «Основы классической механики и их роль в преподавании механики» (Москва, 1-8 октября 1985 г). Выдающиеся учёные разругались и разошлись, не решив окончательно проблемы.
Факторы, влияющие на равновесие системы
Равновесие системы – это состояние, при котором все силы, действующие на систему, сбалансированы и не вызывают никаких изменений в ее движении или форме. Оно является важным понятием в физике, которое позволяет анализировать и предсказывать поведение системы.
- Силы действия: равновесие системы зависит от сил, действующих на нее. Если все силы, действующие на систему, сбалансированы, то система находится в статическом равновесии. Если силы не сбалансированы, то система будет находиться в динамическом равновесии или двигаться.
- Масса: масса объектов, входящих в систему, может повлиять на ее равновесие. Чем больше масса, тем более инертная будет система и тем сложнее будет изменить ее состояние равновесия.
- Трение: трение между поверхностями может создавать силы, которые могут нарушить равновесие системы. Трение может быть полезным, когда нужно предотвратить скольжение или движение системы.
- Центр тяжести: положение центра тяжести системы также влияет на ее равновесие. Если центр тяжести находится выше опорной точки, система будет неустойчивой и будет стремиться к повороту или падению. Если центр тяжести находится ниже опорной точки, система будет устойчивой и будет стремиться вернуться в исходное состояние.
- Опорные точки: наличие или отсутствие опорных точек влияет на равновесие системы. Опорные точки предоставляют системе место для стабилизации и предотвращают ее движение или изменение формы.
Учет этих факторов позволяет более точно анализировать и понимать равновесие системы. Знание этих принципов играет важную роль во многих областях физики, включая механику, термодинамику и гидростатику.
Принцип относительности Галилея
Ученые смогли сформулировать основные формулы для ускорений объектов. Из нее следует, что движущаяся система отсчета удаляется относительно другой без видимого ускорения. Это закономерно в тех случаях, когда ускорение тел происходит одинаково в разных системах отсчета.
Подобные рассуждения берут начало еще во времена Галилея, когда сформировался принцип относительности. Известно, что по второму закону Ньютона ускорение тел имеет принципиальное значение. От этого процесса зависит относительное положение двух тел в пространстве, скорость физических тел. Тогда все уравнения можно записать одинаковым образом в любой инерциальной системе отсчета. Это говорит о том, что классические законы механики не будут иметь зависимость от положения в инерциальной системе отсчета, как принято действовать при осуществлении исследования.
Наблюдаемое явление также не имеет зависимость от конкретного выбора системы отсчета. Подобные рамки в настоящее время рассматриваются как принцип относительности Галилея. Он вступает в некоторые противоречия с иными догмами физиков-теоретиков. В частности, теория относительности Альберта Эйнштейна предполагает иные условия действия.
Принцип относительности Галилея базируется на нескольких основных понятиях:
- в двух замкнутых пространствах, которые движутся прямолинейно и равномерно относительно друг друга, результат внешнего воздействия всегда будет иметь одинаковое значение;
- подобный результат будет действителен только для любого механического действия.
В историческом контексте изучения основ классической механики, подобная трактовка физических явлений сформировалась во многом, как результат интуитивного мышления Галилея, что подтвердилось в научных трудах Ньютона, когда тот представил свою концепцию классической механики. Однако подобные требования по Галилею могут накладывать на структуру механики некоторые ограничения. Это влияет на ее возможные формулировки, оформление и развитие.
Применение равновесия в реальной жизни
Равновесие является важной концепцией в физике, а законы баланса регулируют почти все аспекты нашей жизни.От того, как мы стоим и идем до строительства зданий и мостов, равновесие является критическим соображением.Понимание того, как работает равновесие и как применять его принципы, может помочь нам улучшить нашу повседневную жизнь и принять более обоснованные решения, когда речь идет о проектировании и строительстве конструкций.В реальной жизни существует много различных применений равновесия, каждое из которых помогает пролить свет на важность этой концепции.В этом разделе мы рассмотрим некоторые из этих приложений более подробно. 1
Архитектура и инженерия: принципы равновесия имеют решающее значение в проектировании и строительстве зданий и мостов.Структуры должны быть разработаны, чтобы противостоять силам гравитации, ветра и других факторов окружающей среды.Архитекторы и инженеры используют законы баланса, чтобы гарантировать, что их конструкции являются стабильными и безопасными.Они также используют равновесие для определения распределения веса и силы в структуре, что может помочь предотвратить структурные сбои и коллапсы
1. Архитектура и инженерия: принципы равновесия имеют решающее значение в проектировании и строительстве зданий и мостов.Структуры должны быть разработаны, чтобы противостоять силам гравитации, ветра и других факторов окружающей среды.Архитекторы и инженеры используют законы баланса, чтобы гарантировать, что их конструкции являются стабильными и безопасными.Они также используют равновесие для определения распределения веса и силы в структуре, что может помочь предотвратить структурные сбои и коллапсы.
2
Спорт и легкая атлетика: равновесие также важно в спорте и легкой атлетике.Спортсмены должны поддерживать равновесие и контролировать свои движения, чтобы выступать в своих лучших проявлениях.Они используют центр тяжести своего тела, чтобы поддерживать баланс и контроль, что важно в таких действиях, как гимнастика, фигурное катание и сноуборд.Понимание принципов равновесия может помочь спортсменам улучшить свою производительность и снизить риск получения травм
3. Анатомия и физиология человека: равновесие является фундаментальной концепцией анатомии и физиологии человека.Наши тела должны поддерживать деликатный баланс жидкостей, электролитов и других веществ, чтобы правильно функционировать.Нервная система и эндокринная система работают вместе, чтобы регулировать и поддерживать этот баланс.Понимание того, как равновесие работает в организме, может помочь нам сделать здоровый выбор и предотвратить такие заболевания, как обезвоживание и дисбаланс электролита.
4
Транспортировка: равновесие имеет важное значение для проектирования и эксплуатации транспортных систем.Транспортные средства должны быть разработаны, чтобы поддерживать баланс и стабильность на дороге, в воздухе и на воде.Инженеры используют принципы равновесия для проектирования автомобилей, которые являются безопасными и надежными, и для обеспечения того, чтобы они могли противостоять силам природы и окружающей среды
5
Наука окружающей среды: равновесие также важно в экологической науке.Экосистемы Земли должны поддерживать деликатный баланс живых организмов, питательных веществ и ресурсов для правильного функционирования.Человеческая деятельность, такая как загрязнение и вырубка лесов, могут нарушить этот баланс и привести к экологическим проблемам, таким как изменение климата, разрушение среды обитания и вымирание видов
Равновесие является критической концепцией в физике, которая имеет много применений в реальной жизни.От дизайна зданий и мостов до функционирования нашего тела и здоровья нашей планеты, понимание равновесия имеет важное значение для принятия обоснованных решений и улучшения качества нашей жизни. Применение равновесия в реальной жизни — равновесие по физике: раскрыть законы баланса
Применение равновесия в реальной жизни — равновесие по физике: раскрыть законы баланса




























