Определение угла
Углы — это простые геометрические фигуры. Определение угла напрямую связано со значением радиуса.
Радиус — это прямая линия, которая имеет начало, но не имеет конца и простирается только в одном направлении.
Если дана прямая A на плоскости и точка o на этой прямой, то она преобразуется в две части. Каждая часть линии представляет собой радиус с началом в точке o.
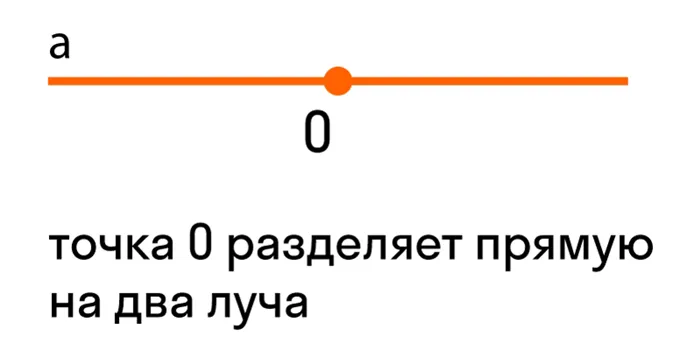
Радиус символизируется буквой латинского алфавита или двумя строчными буквами. Например.
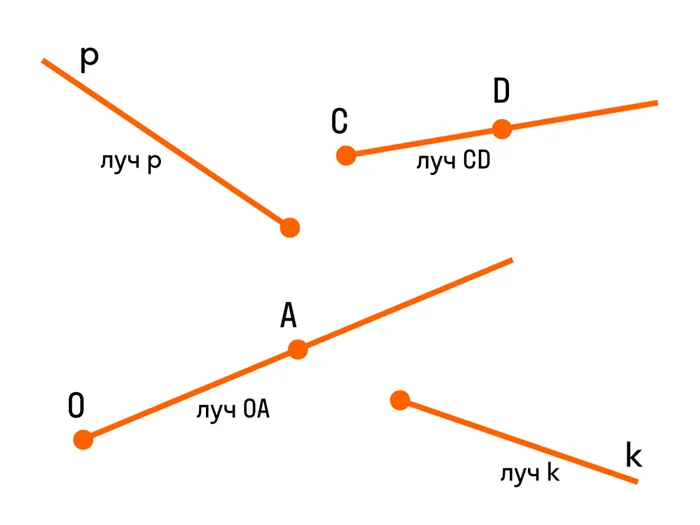
Угол — это часть уровня между двумя прямыми линиями, начинающимися из одной точки. Обе стороны угла являются радиусами, а вершина — общим принципом сторон.

Что такое вершина и стороны угла?
В математике существует специальный символ для обозначения углов — ¶.
Когда стороны угла называются маленькими латинскими буквами, они пишутся после символа. Например, ∠AB или ∠BA.
Когда стороны угла обозначаются заглавными буквами, символ угла и три буквы составляют угол, при этом вершина всегда пишется посередине. Если стороны угла равны OA и OB, то названия угла записываются как ∠AOB и NOBOA. Вы также можете назвать угол с большой буквы, обозначающей вершину.
Может быть цифровая идентификация — это тоже возможно.
Например, все способы наименования угла:.

Если угол делит уровень на две части, то одна будет внутренней областью угла, а другая — внешней. Например:.

Единицей измерения угла является градус. Символ для обозначения градуса угла: °.
Свойства углов
Рассмотрим свойства углов треугольника:
- против большей стороны лежит больший угол, а также наоборот — против большого угла лежит большая сторона;
- напротив равных сторон располагаются равные углы, а также наоборот — напротив равных углов находятся равные стороны (даже если все углы в равностороннем треугольнике равны);
- сумма углов треугольника равняется 180° (таким образом, каждый угол в равностороннем треугольнике равняется 60°);
- если продолжить одну из сторон треугольника, получится внешний угол;
- любая сторона треугольника будет меньше суммы двух иных сторон, а также больше их разности:a < b+c; a > b−c; b < a+c; b > a−c; c < a+b; c > a−b;
- если две параллельные прямые пересекаются секущей, то соответствующие углы равны;
- две плоскости можно назвать перпендикулярными, если двугранный угол между ними равняется 90°.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
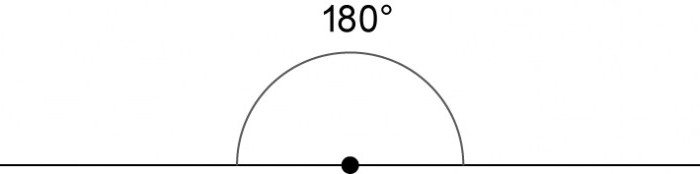
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О
, и сторонами k
и m
.
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Нахождение углов
Как найти углы в прямоугольном треугольнике
Углы в прямоугольном треугольнике возможно найти при помощи двух универсальных способов, которые обрисованы выше, либо с помощью тригонометрических функций — косинуса, синуса, котангенса, тангенса.
Тригонометрические функции
Если даются две стороны, то возможно найти угол по данному алгоритму:
- нужно определить, какими являются стороны в отношении к прямому углу (гипотенуза или катет) и углу, который следует найти (противолежащий\прилежащий катету);
- нужно найти тригонометрическую функцию, подходящую по смыслу решения задачи;
- нужно найти значение тригонометрической функции, подставив все значения сторон;
- нужно вычислить угол с помощью обратной функции (арккосинус, арксинус и др).
Виды углов между прямыми, основные примеры
4.2
Средняя оценка: 4.2
Всего получено оценок: 212.
4.2
Средняя оценка: 4.2
Всего получено оценок: 212.
Углы – это такая же характеристика фигуры, как стороны, периметр или площадь. С помощью углов можно понять, какая фигуры перед нами и какой именно ее вид. Если это треугольник, то по углу визуально можно определить, прямоугольный ли это треугольник, тупоугольный или произвольный, а по общему углу можно доказать равенство или подобие фигур.
Определение
Что такое угол? Существует три определения угла. Рассмотрим каждое из них, выберем наиболее простое и понятное.
Угол – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. То есть это просто два луча. Это определение дается практически в каждом учебнике геометрии. Оно правильное, но прочитав его, не совсем понятно, откуда берется значение угла.
Угол – это плоскость, ограниченная двумя лучами, исходящими из одной точки.
Угол – это мера поворота луча, вокруг своего начала. Это сложно понять, но легко представить. Представьте часы. Вот на часах 12 часов дня, минутная и часовая стрелка находятся на одном уровне, тут минутная стрелка начинает двигаться. И каждый раз, время, а значит положение стрелок можно определить именно углом между часовой и минутной стрелкой. Углы могут быть разными, но если выделять угол в каждый момент времени дугой, то можно заметить, что дуга в конце концов превратится в круг.
Именно круг и является началом отчета для градуса. Дуга $$1\over360$$ части круга это градус. А по количеству градусов в угле можно выделить основные виды углов между прямыми: острые, прямые, тупые и полные углы.
Виды углов: острый, прямой, тупой, полный
Острый угол это угол, значение которого меньше 90 градусов.![]()
Прямой угол
Прямой угол очень много значит в геометрии. Прямой угол в параллелограмме, означает, что перед вами квадрат или прямоугольник. Произвольный треугольник, если доказать, что в нем есть прямой угол, сразу же превращается в прямоугольный треугольник, для которого действует больший набор теорем и правил, нежели для произвольного.
Тупой угол
Тупой угол, это угол больше 90 градусов. Это значение очень широко используется в задачах по тригонометрии. Но и в геометрии очень часто можно встретить задачи на тупоугольный треугольник. Считается, что тупоугольный треугольник сложнее воспринимается чисто визуально, но на деле, стоит только привыкнуть и задачи эти уже не будут казаться такими страшными.![]()
Полный угол
Полный угол это угол в 360 градусов. То есть тот самый момент, когда минутная и часовая стрелка совпадает.
Тогда с одной стороны будет полный угол, а с другой угол в 0 градусов. Чисто теоретически и нулевой угол тоже существует, он означает, что стрелки или лучи друг от друга не отклонялись.
Что мы узнали?
Мы узнали, что такое угол, определили виды углов, поговорили о том, какую роль каждый из видов играет в геометрии и привели примеры каждого из них.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Елена Никитина
10/10
-
Бетти Нуар
10/10
-
Ольга Журавлева
10/10
-
Валерия Качанова
10/10
-
Артём Мещеряков
9/10
Теорема Пифагора
Теорема основана на утверждении, что в прямоугольном треугольнике сумма квадратов длин перпендикулярных линий равна квадрату длины гипотенузы. В пресс-релизе говорится, что
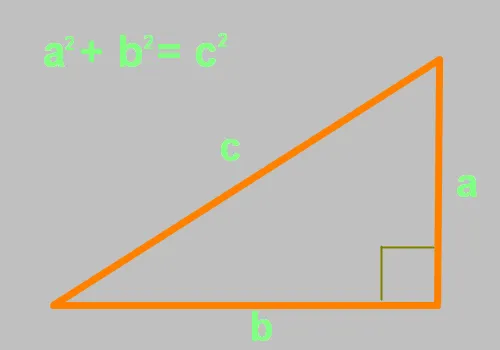
Стороны a и b — катеты, угол между которыми составляет ровно 90 градусов. Таким образом, сторона c является косой. Подставив две известные величины в это уравнение, можно рассчитать третью неизвестную величину. В результате можно регистрировать и контролировать правильный угол.
Теорема Пифагора также известна как «египетский треугольник». Это треугольник со сторонами 3, 4 и 5; единицы длины не имеют значения. Расстояние между сторонами 3 и 4 составляет ровно 90 градусов. Проверим это утверждение с помощью приведенного выше уравнения: a²+b²=c²= (3 x 3) + (4 x 4) = 9 + 16 = (5 x 5) = 25- все сходится!
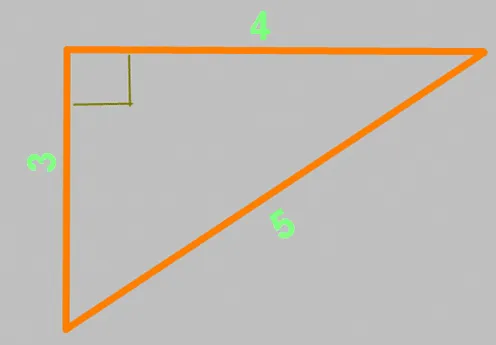
Теперь давайте применим теорему на практике.
Признаки и свойства острых углов
Перечислим свойства, которые характерны для любого острого угла:
- При рассмотрении пары смежных углов, один из которых меньше по сравнению с прямым, то есть определяется как острый, можно сделать вывод, что второй из смежных углов является тупым.
- Какой-либо произвольный треугольник обладает как минимум одним острым углом.
- Треугольники, которые образованы тремя острыми углами, носят название остроугольных.
Признаком любого острого угла является его градусная мера, которая в любом случае будет меньше, чем 90°. В геометрии часто встречаются задачи, когда необходимо идентифицировать тот или иной угол по его признаку. Тогда целесообразно воспользоваться еще одним полезным инструментом под названием угольник.
В качестве примера воспользуемся угольником и соединим его вершину с вершиной искомого угла, который необходимо идентифицировать. При этом расположим угольник так, чтобы его грань проходила по какой-нибудь одной стороне рассматриваемого угла. В результате другая сторона измерительного инструмента перекроет вторую сторону угла. Изобразим схематично принцип выполнения этой процедуры:
Геометрический угол: определение и основные характеристики
Основными характеристиками геометрического угла являются его мера и классификация по величине.
Мера угла измеряется в градусах, минутах и секундах. Градус — основная единица измерения углов. Он равен 1/360 от полного оборота. Кроме градусов, угол может быть измерен в минутах и секундах. 1 градус равен 60 минутам, а 1 минута равна 60 секундам.
Классификация геометрических углов по величине включает прямой угол, острый угол и тупой угол. Прямой угол равен 90 градусов, острый угол меньше 90 градусов, а тупой угол больше 90 градусов.
Смежные углы — это углы, которые имеют общую сторону и общую вершину, но различные стороны. Сумма мер смежных углов равна 180 градусов.
Вертикальные углы — это пара углов, которые находятся напротив друг друга и образуют линию. Вертикальные углы всегда равны друг другу.
Геометрические углы широко используются в повседневной жизни. Например, при измерении углов в строительстве или при интерпретации карт. Понимание основных характеристик геометрических углов помогает в решении задач и анализе геометрических форм в различных областях знаний.
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). Лучи, образующие угол
, называют сторонами угла, а точку, из которой они выходят, — вершиной угла. На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки
М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.

Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
\ и \ полностью совмещаются при наложении следовательно: \
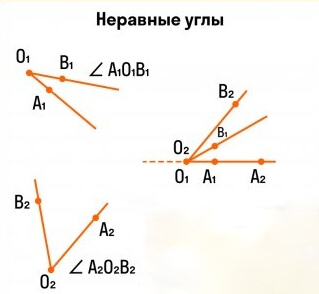
\ и \ не совмещаются при наложении: \
Причем: \
При этом развернутые углы всегда являются равными.
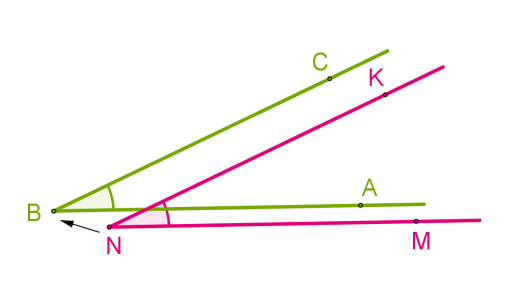
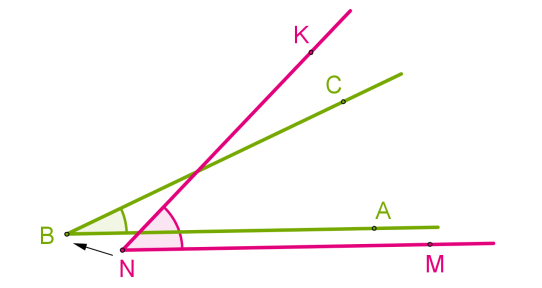
Совмещение углов \ и \ происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Виды углов
Существует несколько типов углов, и каждый имеет свое название.
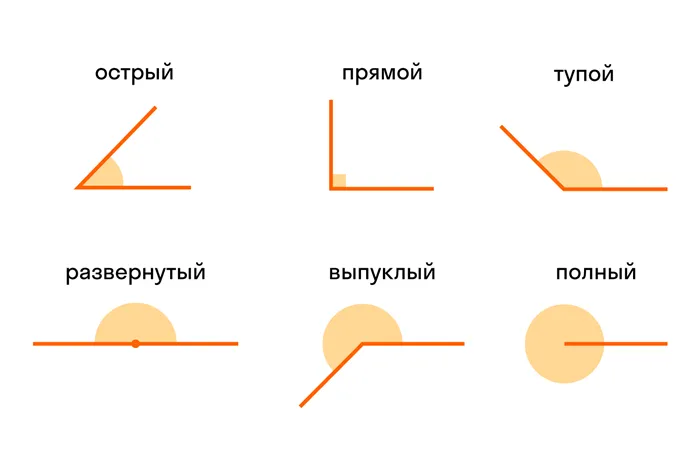
В геометрии важно различать типы углов. Это можно сделать на глаз или с помощью линейки
Прямые углы — это углы, стороны которых перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два соседних угла равны между собой, то каждый из них является прямым углом. Для удобства прямые углы символизируются углами. Например, так:.
На изображении показаны два правильных угла Шипл — AOC и NOCOB. Общая сторона OC перпендикулярна прямой AB, а точка O является основанием перпендикуляра.
Острые углы — это прямые углы, т.е. углы с малыми углами.
Открытый угол — это открытый угол, образованный двумя лучами света, равный сумме двух правильных углов. Открытый угол равен 180°. Как выглядит разработанный угол, показано на первом рисунке.
Когда развернутый угол делится на плоскости, каждая часть угла считается внутренней областью развернутого угла.
Неравный угол — это любой угол, который не является вычитаемым углом. Другими словами, она не равна 180°.
Тупые углы — это углы, которые больше прямых, но являются углами развития (меньше 90°).
Выпуклый угол — это угол, который больше прямого угла, но меньше полного (180°).
Полные углы — это углы, обе стороны которых имеют одинаковый радиус. Это равно сумме четырех правильных углов, т.е. = 360°.
Смежные углы — это пары углов с общей вершиной и стороной, причем другая сторона находится на противоположной стороне от общей стороны.
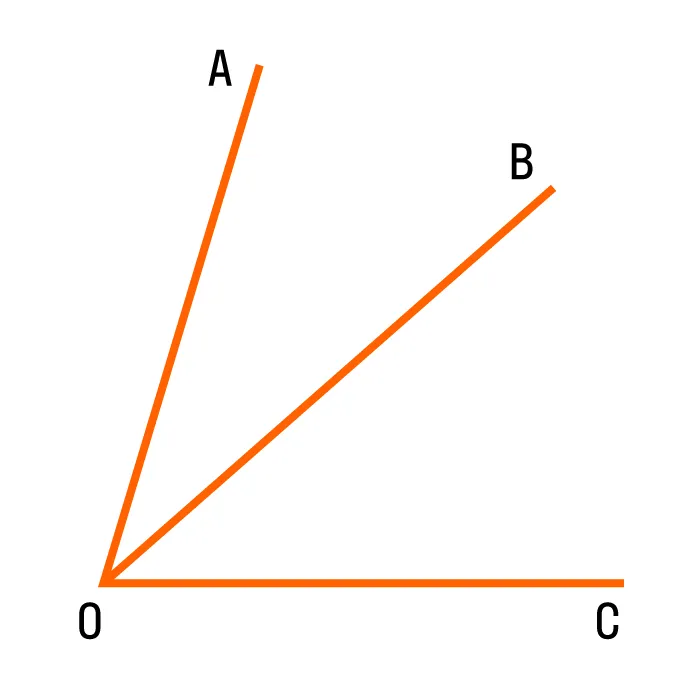
На рисунке изображены два смежных угла anob и ∠BOC, с общей вершиной o, общей ob.
Это определение может быть сформулировано по-разному. Если радиус вычитается из вершины угла, делящего угол на два, то образовавшиеся углы являются смежными.
Чтобы разделить угол на радиус, прибавьте угол. Из этого можно выделить следующие корректные различия.
Углы называются прямыми, если они равны 90°, острыми, если они меньше 90°, и тупыми, если они больше 90° и меньше 180°. Открытый угол равен 180°.
Онлайн-школа Skysmart поощряет детей и подростков к занятиям математикой. За интересные задачи, знание новых приложений и хорошие оценки!
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
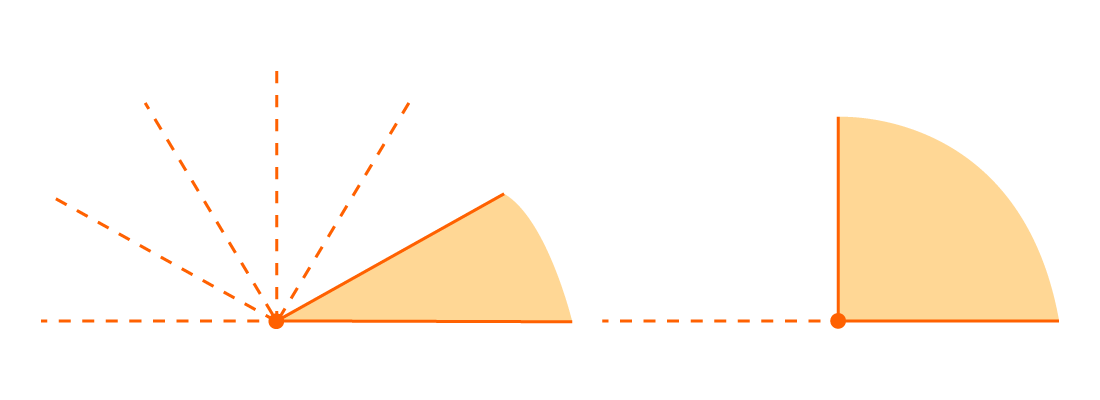
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
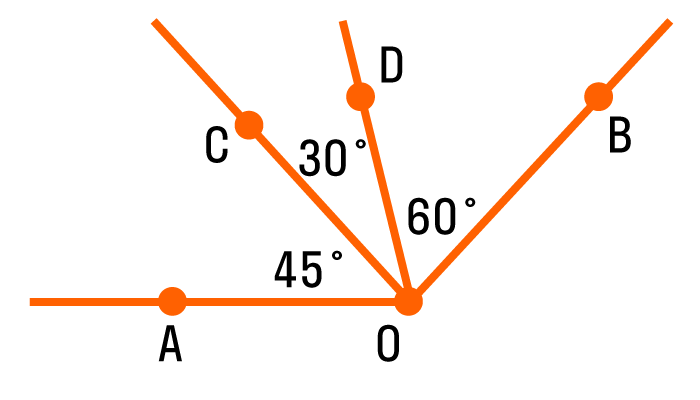
Равные углы имеют равную градусную меру.
Понятие углов, виды углов
Обычно для названия углов используют три заглавные буквы. Ими обозначаются две точки, которые расположены на сторонах угла, а также вершины.
Посмотрите на рисунок:
Величина угла измеряется в градусах. Например, ∠AOB=24°.
Существует также другое определение угла.
Развернутым углом называется угол, при котором обе стороны угла располагаются на одной прямой (его стороны считаются дополнительными полупрямыми на одной прямой).
Посмотрите на рисунок развернутого угла:
Вершиной угла считается точка на данной прямой. Обычно в геометрии вершину угла называют точкой O. В математике угол обозначают обычно специальным знаком — . Если стороны угла подписать малыми латинскими буквами, то для точного определения угла записывают друг после друга буквы, которые соответствуют сторонам.
Если используется обозначение с помощью больших букв, то стороны угла будут иметь названия OB, OA. В данном случае у угла появляется обозначение из трех латинских букв, которые записаны друг за другом, с вершиной в центре — ∠AOB, ∠BOA. Используется также обозначение с помощью цифр. Используется в том случае, когда у углов нет названий, а также обозначений в виде букв.
Посмотрите на разные обозначения углов:
Угол может делить плоскость на две части. Если угол не является развернутым, тогда меньшая часть плоскости носит название внутренней области угла, большая часть называется внешней областью угла.
Посмотрите, какие части являются внешними, а какие внутренними:
Если развернутый угол разделяется на плоскости, любая из его частей является внутренней областью развернутого угла. Внутренняя область угла считается таким элементом, который служит для вторичного определения угла.
Определение смежных и вертикальных углов
Обратите внимание на рисунок ниже, на котором видно, что смежные углы являются дополнением друг друга до развернутого угла. Посмотрите на вертикальные углы:
Посмотрите на вертикальные углы:
В случае пересечения прямых формируются 4 пары смежных углов, а также 2 пары вертикальных углов.
Посмотрите на то, как это выглядит:
Бывает несколько видов углов:
- острый угол (менее 90°);
- тупой угол (более 90°);
- прямой угол (ровно 90°);
- развернутый угол (ровно 180°).
Посмотрите, как они выглядят:
Также стоит упомянуть о накрест лежащих углах. Накрест лежащими углами называются углы, которые расположены во внутренней области в разных сторонах от секущей (то есть накрест друг от друга).
Также вспомним соответственные углы. Это вид углов, которые образуются в случае пересечения двух параллельных прямых общей секущей.
Свойства вертикальных углов:
- вертикальные углы являются равными (∠AOC=∠BOD, ∠COD=∠AOB);
- биссектрисы вертикальных углов лежат на одной прямой.
Свойства смежных углов:
- сумма смежных углов равняется 180°;
- угол, который является смежным с прямым, является прямым; смежный с острым — является тупым; смежный с тупым — является острым;
- если два угла равны, то смежные тоже будут равны;
- чем больше угол, тем смежный меньше;
- биссектрисы смежных углов формируют прямой угол;
- если смежные равны, то они являются прямыми.
Определение и измерение
 Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита,
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части:
- внутренняя в планиметрии не превышает 180 градусов,
- внешняя.
Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).

Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
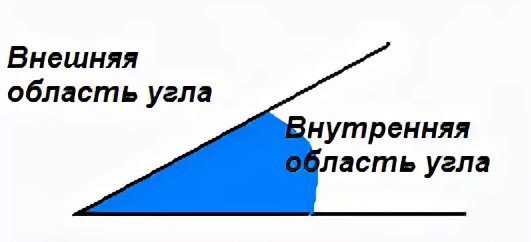
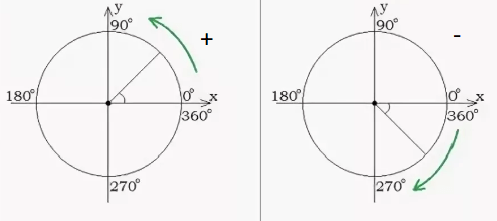
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
-
Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. -
Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
-
Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. -
Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. -
Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.

Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус
. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура
, что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Геометрические фигуры с развернутыми углами
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.
∠ABD в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.
Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.
Углы треугольника и их влияние на его свойства
В треугольнике всегда существуют три угла, которые определяют его форму и свойства. Знание значений этих углов позволяет нам лучше понять структуру треугольника и рассмотреть его особенности. Ниже мы рассмотрим, как различные значения углов влияют на треугольник.
Остроугольный треугольник
В остроугольном треугольнике все три угла меньше 90 градусов. Такой треугольник имеет следующие особенности:
- Все стороны остроугольного треугольника положительны и имеют конечную длину.
- Остроугольный треугольник не имеет параллельных сторон.
Прямоугольный треугольник
Прямоугольный треугольник имеет один угол, равный 90 градусов. Он обладает следующими свойствами:
- Противоположные стороны прямого угла называются гипотенузой и катетами.
- Катеты прямоугольного треугольника всегда положительны и имеют конечную длину.
- Гипотенуза прямоугольного треугольника может быть любой длины, включая нуль.
Тупоугольный треугольник
В тупоугольном треугольнике один из углов больше 90 градусов. Такой треугольник обладает следующими особенностями:
- Одна из сторон тупоугольного треугольника может быть отрицательной или иметь бесконечную длину.
- Тупоугольный треугольник может иметь параллельные стороны, если его один угол равен 180 градусов.
Равносторонний треугольник
Равносторонний треугольник имеет три равные стороны и три равных угла, каждый из которых равен 60 градусов. Этот тип треугольника имеет следующие свойства:
- Все стороны равностороннего треугольника положительны и имеют одинаковую длину.
- Углы равностороннего треугольника равны 60 градусов.
- Равносторонний треугольник является примером регулярного многоугольника.
Изучение углов треугольника позволяет лучше понять его конструкцию и свойства. Знание этих особенностей поможет в решении геометрических задач и рассмотрении различных особенностей треугольника в приложениях математики и физики.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым
углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Определение и особенности развернутого угла
Развернутый угол — это угол, у которого мера равна 180 градусам или π (пи) радианам. Развернутый угол представляет полный оборот или полную окружность.
Особенности развернутого угла:
- Мера развернутого угла всегда равна 180 градусам или π (пи) радианам;
- Развернутый угол имеет характеристики, которые присущи всем углам, такие как вершина, стороны и смежные углы;
- Развернутый угол можно представить как полную окружность или оборот;
- В градусной мере развернутый угол занимает половину от полного оборота (360 градусов).
Примеры развернутого угла:
| Угол | Мера |
|---|---|
| α | 180 градусов / π радианов |
| β | 180 градусов / π радианов |
| γ | 180 градусов / π радианов |
Все приведенные выше углы являются развернутыми, так как их мера равна 180 градусам или π (пи) радианам.
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию
В каждом из них немалое внимание уделяется углам:
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии
Виды углов
lass=»defenition8″ id=»types_of_angles_in_geometry» ssmarticle>
ÐÐ¸Ð´Ñ Ñглов в геомеÑÑии â ÑÑо ÑазлиÑнÑе ÑглÑ, клаÑÑиÑиÑиÑÑемÑе по Ð¸Ñ Ð³ÑадÑÑной меÑе:
- ÐÑÑÑÑй Ñгол: Ð¾Ñ 0° до 90° (не вклÑÑÐ°Ñ 90°). ÐÑимеÑ: Ñгол 45°.
- ÐÑÑмой Ñгол: Ñавен 90°. СÑоÑÐ¾Ð½Ñ Ð¿ÐµÑпендикÑлÑÑнÑ. ÐÑимеÑ: Ñгол Ð¼ÐµÐ¶Ð´Ñ ÑÑоÑонами квадÑаÑа.
- ТÑпой Ñгол: Ð¾Ñ 90° до 180° (не вклÑÑÐ°Ñ 180°). ÐÑимеÑ: Ñгол 120°.
- РазвÑÑнÑÑÑй Ñгол: Ñавен 180°. ÐÑимеÑ: пÑÑÐ¼Ð°Ñ Ð»Ð¸Ð½Ð¸Ñ.
- ÐолнÑй Ñгол: Ñавен 360°. ÐÑимеÑ: кÑÑг.
ÐÑÑÑ ÑазнÑе ÑÐ¸Ð¿Ñ Ñглов и Ñ ÐºÐ°Ð¶Ð´Ð¾Ð³Ð¾ ÑÐ²Ð¾Ñ Ð½Ð°Ð·Ð²Ð°Ð½Ð¸Ðµ:
- оÑÑÑÑй
- пÑÑмой
- ÑÑпой
- ÑазвеÑнÑÑÑй
- вÑпÑклÑй
- полнÑй
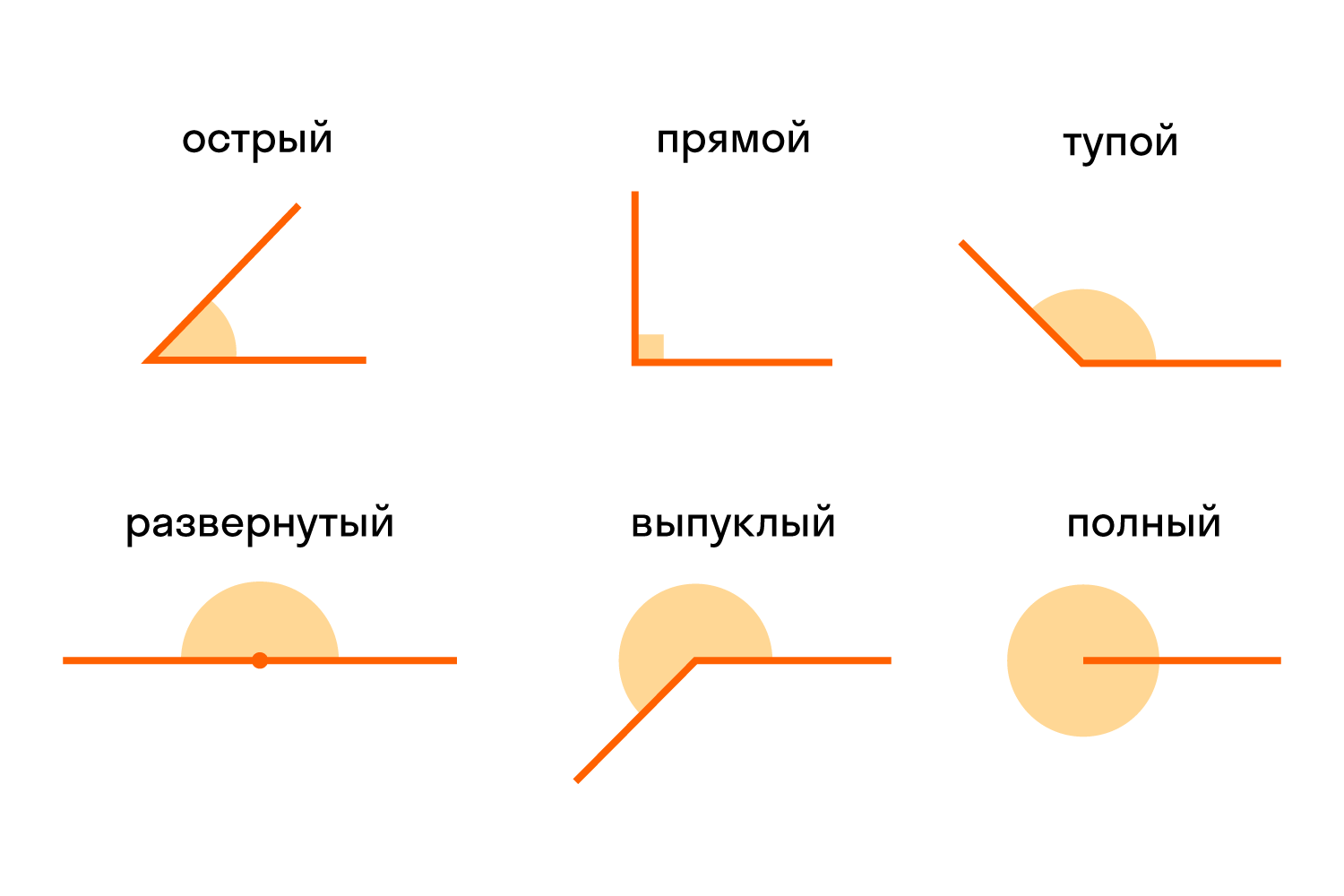
РазлиÑаÑÑ Ð²Ð¸Ð´Ñ Ñглов в геомеÑÑии важно. ÐпÑеделÑÑÑ Ð¼Ð¾Ð¶Ð½Ð¾ на глаз или Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ Ð»Ð¸Ð½ÐµÐ¹ÐºÐ¸.
ÐÑÑмой Ñгол â ÑÑо Ñгол, ÑÑоÑÐ¾Ð½Ñ ÐºÐ¾ÑоÑого пеÑпендикÑлÑÑÐ½Ñ Ð´ÑÑг дÑÑгÑ. ÐÑÑмой Ñгол вÑегда Ñавен 90°.
ÐÑли два ÑмежнÑÑ Ñгла ÑÐ°Ð²Ð½Ñ Ð¼ÐµÐ¶Ð´Ñ Ñобой, Ñо каждÑй из Ð½Ð¸Ñ ÑвлÑеÑÑÑ Ð¿ÑÑмÑм. ÐÐ»Ñ ÑдобÑÑва пÑÑмой Ñгол обознаÑаеÑÑÑ Ñголком. ÐÐ¾Ñ Ñак:
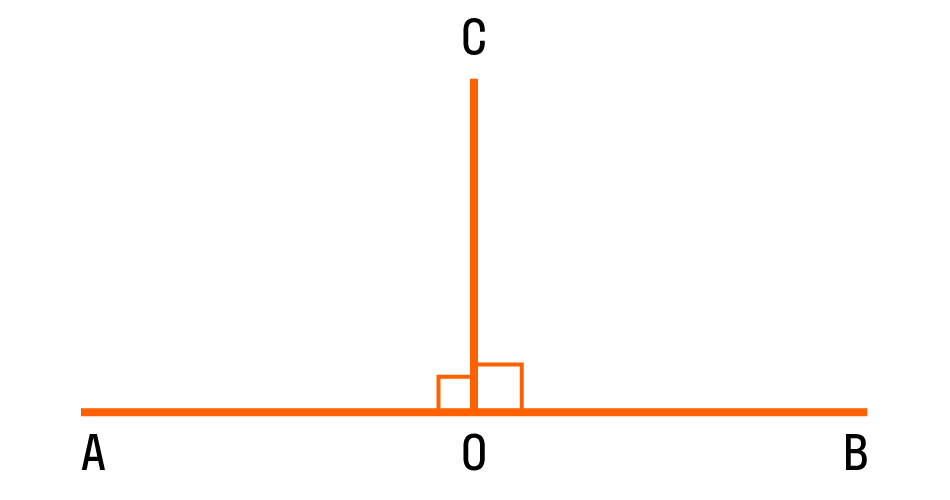
Ðа каÑÑинке изобÑÐ°Ð¶ÐµÐ½Ñ Ð´Ð²Ð° пÑÑмÑÑ Ñгла â AOC и â COB. ÐбÑÐ°Ñ ÑÑоÑона OC пеÑпендикÑлÑÑна пÑÑмой AB, а ÑоÑка O â оÑнование пеÑпендикÑлÑÑа.
ÐÑÑÑÑй Ñгол â ÑÑо Ñгол, коÑоÑÑй менÑÑе пÑÑмого Ñгла, Ñо еÑÑÑ < 90°.
РазвеÑнÑÑÑй Ñгол â ÑÑо оÑкÑÑÑÑй Ñгол, коÑоÑÑй обÑазован двÑÐ¼Ñ Ð»ÑÑами и Ñавен ÑÑмме двÑÑ Ð¿ÑÑмÑÑ Ñглов. РазвеÑнÑÑÑй Ñгол Ñавен 180°. Ðак вÑглÑÐ´Ð¸Ñ ÑазвеÑнÑÑÑй Ñгол, показано на пеÑвой каÑÑинке.
ÐÑи Ñазделении ÑазвеÑнÑÑÑм Ñглом на плоÑкоÑÑи лÑÐ±Ð°Ñ Ð¸Ð· его ÑаÑÑей ÑÑиÑаеÑÑÑ Ð²Ð½ÑÑÑенней облаÑÑÑÑ ÑазвеÑнÑÑого Ñгла.
ÐеÑазвеÑнÑÑÑй Ñгол â ÑÑо лÑбой Ñгол, коÑоÑÑй не ÑвлÑеÑÑÑ ÑазвеÑнÑÑÑм, Ñо еÑÑÑ Ð½Ðµ Ñавен 180°.
ТÑпой Ñгол â ÑÑо Ñгол, коÑоÑÑй болÑÑе пÑÑмого Ñгла, но менÑÑе ÑазвеÑнÑÑого:
90° < ÑÑпой Ñгол < 180°.
ÐÑпÑклÑй Ñгол â ÑÑо Ñгол, коÑоÑÑй болÑÑе ÑазвеÑнÑÑого Ñгла, но менÑÑе полного:
180° < вÑпÑклÑй Ñгол < 360°.
ÐолнÑй Ñгол â ÑÑо Ñгол, обе ÑÑоÑÐ¾Ð½Ñ ÐºÐ¾ÑоÑого ÑовпадаÑÑ Ñ Ð¾Ð´Ð½Ð¸Ð¼ лÑÑом. Ðн Ñавен ÑÑмме ÑеÑÑÑÐµÑ Ð¿ÑÑмÑÑ Ñглов, Ñо еÑÑÑ = 360°.
ÐÑилежаÑие ÑÐ³Ð»Ñ â ÑÑо паÑа Ñглов Ñ Ð¾Ð±Ñей веÑÑиной и ÑÑоÑоной, дÑÑгие ÑÑоÑÐ¾Ð½Ñ Ð¿Ñи ÑÑом Ð»ÐµÐ¶Ð°Ñ Ð¿Ð¾ ÑазнÑе ÑÑоÑÐ¾Ð½Ñ Ð¾Ñ Ð¾Ð±Ñей ÑÑоÑонÑ.
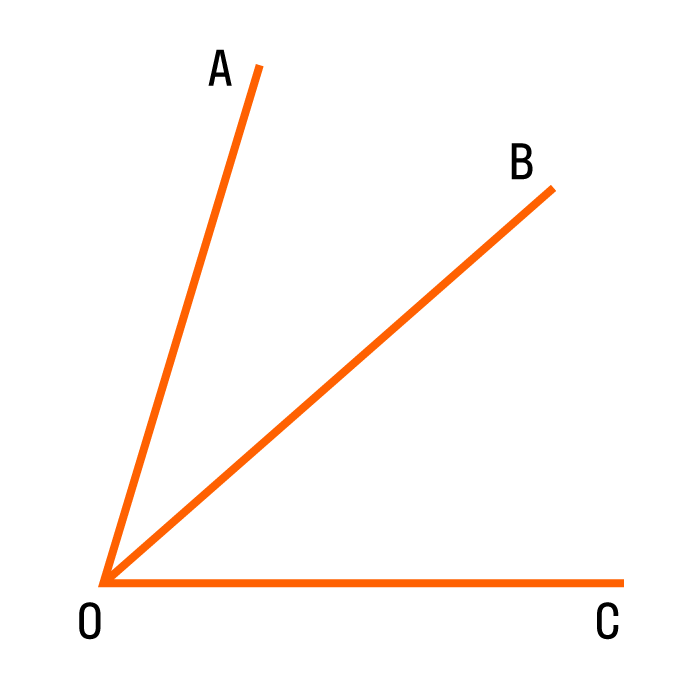
Ðа каÑÑинке Ð¼Ñ Ð²Ð¸Ð´Ð¸Ð¼ два пÑилежаÑÐ¸Ñ Ñгла â AOB и â BOC, обÑÑÑ Ð²ÐµÑÑÐ¸Ð½Ñ O и обÑÑÑ ÑÑоÑÐ¾Ð½Ñ OB.
Ðожно ÑÑоÑмÑлиÑоваÑÑ Ð¾Ð¿Ñеделение по-дÑÑгомÑ: еÑли из веÑÑÐ¸Ð½Ñ Ð»Ñбого Ñгла пÑовеÑÑи лÑÑ, ÑазделÑÑÑий Ñгол на два, Ñо обÑазованнÑе ÑÐ³Ð»Ñ Ð±ÑдÑÑ Ð¿ÑилежаÑими.
ЧÑÐ¾Ð±Ñ Ð½Ð°Ð¹Ñи Ñгол, коÑоÑÑй Ñазделен лÑÑом, нÑжно ÑложиÑÑ Ð¿Ð¾Ð»ÑÑеннÑе ÑглÑ: â AOB = â AOC + â COB. Ðз ÑÑого можно вÑделиÑÑ ÑледÑÑÑие веÑнÑе ÑазноÑÑи:
- â AOC = â AOB â â COB,
- â COB = â AOB â â AOC.
Ðапоминаем!
Угол назÑваеÑÑÑ Ð¿ÑÑмÑм, еÑли он Ñавен 90°, оÑÑÑÑм, еÑли он менÑÑе 90°, ÑÑпÑм, еÑли он болÑÑе 90°, но менÑÑе 180°. РазвеÑнÑÑÑй Ñгол Ñавен 180°.
Ðнлайн-Ñкола Skysmart пÑиглаÑÐ°ÐµÑ Ð´ÐµÑей и подÑоÑÑков на кÑÑÑÑ Ð¿Ð¾ маÑемаÑике â за инÑеÑеÑнÑми задаÑами, новÑми пÑикладнÑми знаниÑми и ÑоÑоÑими оÑенками!
Топ вопросов за вчера в категории Геометрия
Геометрия 04.05.2019 22:27 75 Агафонов Михаил
К двум окружностям с центрами в точках о1 о2 касающимся внешним образом в точке А, проведена общая
Ответов: 2
Геометрия 23.10.2023 19:27 19 Казяба Иван
Между сторонами угла АОВ, равного 120, взята точка С. Найдите градусную меру угла АОС, если
Ответов: 2
Геометрия 02.07.2023 18:29 7 Гурна Мария
Задумано двузначное число в котором единиц в три раза больше чем десятков
Ответов: 2
Геометрия 21.06.2023 05:54 16 Тулекбаев Айдос
На отрезке КЕ отмечена точка Р Дано: KP — PE = 3 см, KE = 21 см. Найти: КР и РЕ.
Ответов: 2
Геометрия 15.07.2023 21:48 9 Котова Вика
Прямоугольная трапеция В=8см Н=10см Найти Периметр и площадь
Ответов: 2
Геометрия 29.09.2023 09:15 157 Павленко Карина
ПОМОГИТЕ ПЖ!!! ДАЮ 30 БАЛЛОВ!!! Дан правильный пятиугольник ABCDE, M и N — точки пересечения
Ответов: 2
Геометрия 19.06.2023 00:31 832 Линецкий Лукас
Определи значения углов M и K трапеции MNKT.
Ответов: 2
Геометрия 18.06.2023 23:03 107 Емельянова Алёна
Дан куб ABCDA1B1C1D1. Определите взаимное расположение прямых и угол между ними. А) AD и AD1 Б)
Ответов: 2
Геометрия 10.07.2023 03:17 210 Халикова Алия
Угол 1 = 40°угол 2, угол 3, угол 4 – ?д
Ответов: 1
Геометрия 05.10.2023 13:49 8 Романова Софья
В прямоугольной трапеции меньшая диагональ отсекает от неё равносторонний треугольник. Найдите
Ответов: 2


























