Зачем нужна математика

Определение разности двух углов

Разность двух углов — это величина, которая определяется как результат вычитания одного угла из другого. Когда речь идет о разности двух углов, мы имеем в виду разность их мер (в градусах, радианах или градах).

Для определения разности двух углов необходимо вычислить разность их числовых значений. Знак разности углов позволяет определить, какой угол больше: положительный знак говорит о том, что первый угол больше второго, а отрицательный знак — о том, что второй угол больше первого.

Существуют несколько способов задания углов и их разности в математике:

1. Градусы: угол измеряется в градусах, где полный оборот составляет 360 градусов.
2. Радианы: угол измеряется в радианах, где полный оборот составляет 2π радианов.
3. Грады: угол измеряется в градах, где полный оборот составляет 400 градов.

Если заданы два угла в одной и той же системе измерения, разность можно найти путем вычитания значений углов. Если углы заданы в разных системах измерения, их следует сначала перевести в одну и ту же систему, а затем искать разность.

Например, пусть имеются два угла — 120° и 90°. Разность будет равна 120° — 90° = 30°. Знак разности говорит о том, что первый угол больше второго.

Понятие углов, виды углов

Обычно для названия углов используют три заглавные буквы. Ими обозначаются две точки, которые расположены на сторонах угла, а также вершины.

Посмотрите на рисунок:

Величина угла измеряется в градусах. Например, ∠AOB=24°.

Существует также другое определение угла.

Развернутым углом называется угол, при котором обе стороны угла располагаются на одной прямой (его стороны считаются дополнительными полупрямыми на одной прямой).

Посмотрите на рисунок развернутого угла:

Вершиной угла считается точка на данной прямой. Обычно в геометрии вершину угла называют точкой O. В математике угол обозначают обычно специальным знаком — . Если стороны угла подписать малыми латинскими буквами, то для точного определения угла записывают друг после друга буквы, которые соответствуют сторонам.

Если используется обозначение с помощью больших букв, то стороны угла будут иметь названия OB, OA. В данном случае у угла появляется обозначение из трех латинских букв, которые записаны друг за другом, с вершиной в центре — ∠AOB, ∠BOA. Используется также обозначение с помощью цифр. Используется в том случае, когда у углов нет названий, а также обозначений в виде букв.

Посмотрите на разные обозначения углов:

Угол может делить плоскость на две части. Если угол не является развернутым, тогда меньшая часть плоскости носит название внутренней области угла, большая часть называется внешней областью угла.

Посмотрите, какие части являются внешними, а какие внутренними:

Если развернутый угол разделяется на плоскости, любая из его частей является внутренней областью развернутого угла. Внутренняя область угла считается таким элементом, который служит для вторичного определения угла.

Определение смежных и вертикальных углов

Обратите внимание на рисунок ниже, на котором видно, что смежные углы являются дополнением друг друга до развернутого угла. Посмотрите на вертикальные углы:

Посмотрите на вертикальные углы:

В случае пересечения прямых формируются 4 пары смежных углов, а также 2 пары вертикальных углов.

Посмотрите на то, как это выглядит:

Бывает несколько видов углов:

• острый угол (менее 90°);
• тупой угол (более 90°);
• прямой угол (ровно 90°);
• развернутый угол (ровно 180°).

Посмотрите, как они выглядят:

Также стоит упомянуть о накрест лежащих углах. Накрест лежащими углами называются углы, которые расположены во внутренней области в разных сторонах от секущей (то есть накрест друг от друга).

Также вспомним соответственные углы. Это вид углов, которые образуются в случае пересечения двух параллельных прямых общей секущей. 

Свойства вертикальных углов:

• вертикальные углы являются равными (∠AOC=∠BOD, ∠COD=∠AOB);
• биссектрисы вертикальных углов лежат на одной прямой.

Свойства смежных углов:

• сумма смежных углов равняется 180°;
• угол, который является смежным с прямым, является прямым; смежный с острым — является тупым; смежный с тупым — является острым;
• если два угла равны, то смежные тоже будут равны;
• чем больше угол, тем смежный меньше;
• биссектрисы смежных углов формируют прямой угол;
• если смежные равны, то они являются прямыми.

Математика в науке и исследованиях

Математика играет фундаментальную роль в науке и исследованиях. Она не только даёт нам инструменты для измерения и анализа данных, но и является самой основой многих научных теорий.

В физике, например, математические модели помогают исследовать процессы, которые не могут быть наблюдаемы непосредственно, а также прогнозировать поведение систем в различных условиях. Так, уравнения Ньютона позволяют объяснять движение тел в пространстве, а уравнения Максвелла дают описание электромагнитных явлений.

Математика является важной частью и в других научных областях, таких как биология, генетика и экономика. В биологии, например, математические модели помогают исследовать популяции животных и растений, а также прогнозировать их поведение в различных экологических условиях

Однако математика не только помогает нам понять мир вокруг нас, но и открывает новые горизонты для научных исследований. Многие математические теории ранее не находили практического применения, но позже стали основой для разработки новых технологий.

Таким образом, математика играет центральную роль в научных исследованиях, обеспечивая науке источник новых идей и инструменты для их реализации.

Вопрос-ответ:

Почему математика считается основой науки?

Математика является основой науки из-за ее системных и логических подходов, которые позволяют абстрагировать реальные явления и описывать их в виде формул и уравнений. Это позволяет разрабатывать более точные и точные модели, которые затем могут быть использованы для предсказания различных явлений.

Как математика используется в технологиях?

Математика используется в технологиях для создания различных алгоритмов и способов оптимизации производственных процессов. К примеру, математические алгоритмы используются для оптимизации сетей машинного обучения, что позволяет ускорять обучение и получать более точные результаты.

Какие математические концепции используются в экономике?

В экономике используются многие математические концепции, такие как геометрия, теория вероятности, анализ функций, дифференциальные уравнения и т.д. Они используются для моделирования различных явлений, например, для определения оптимальных цен на товары, прогнозирования спроса и т.д.

Как математика связана с развитием компьютерных игр?

Математика используется в разработке компьютерных игр для создания реалистичной физики, графики и искусственного интеллекта. Также математические алгоритмы используются для создания карт и генерации мира, что позволяет игрокам иметь различные варианты переживания игрового процесса.

Как математика помогает в изучении климата и географии?

Математика используется в изучении климата и географии для моделирования и прогнозирования различных явлений, как например, изменение климата, изменение уровня воды, сейсмические активности и т.д. Также математические модели позволяют улучшить метеорологическую и гидрологическую прогнозную системы.

Какие свойства математических объектов могут иметь практическое применение?

Математические объекты, такие как графы, матрицы, дифференциальные уравнения и т.д., имеют множество свойств, которые могут быть использованы для решения различных практических задач. Например, свойства графов используются в моделировании транспортных и коммуникационных сетей, а свойства матриц используются в теории решения линейных уравнений и обработке данных.

Что такое теория игр в математике?

Теория игр — это раздел математики, который занимается исследованием стратегий и принятия решений в конфликтных ситуациях. Она может быть применена в различных областях, таких как экономика, политика, бизнес и т.д. Теория игр позволяет разрабатывать математические модели конфликтных ситуаций и определять оптимальные стратегии для каждого участника игры.

Как математика может помочь в повседневной жизни?

Математика может помочь в повседневной жизни в различных сферах, например, при расчете бюджета, выборе инвестиций, создании графиков и диаграмм, что позволяет более точно понимать различные явления и принимать взвешенные решения. Также математика помогает развивать стратегическое мышление и логику.

Общие сведения

Основными элементами, используемыми в геометрии, являются лучи и углы. С их помощью образуется любая геометрическая фигура — квадрат, треугольник или любого вида многоугольник. Луч — это полупрямая, то есть часть линии, на которой точки располагаются по одной стороне от зафиксированной. По-другому можно сказать, что луч — это линия, ограниченная только с одной стороны. Обозначают его как прописными латинскими буквами, так и заглавными с названием точек. Во втором случае первой указывается начальная точка.

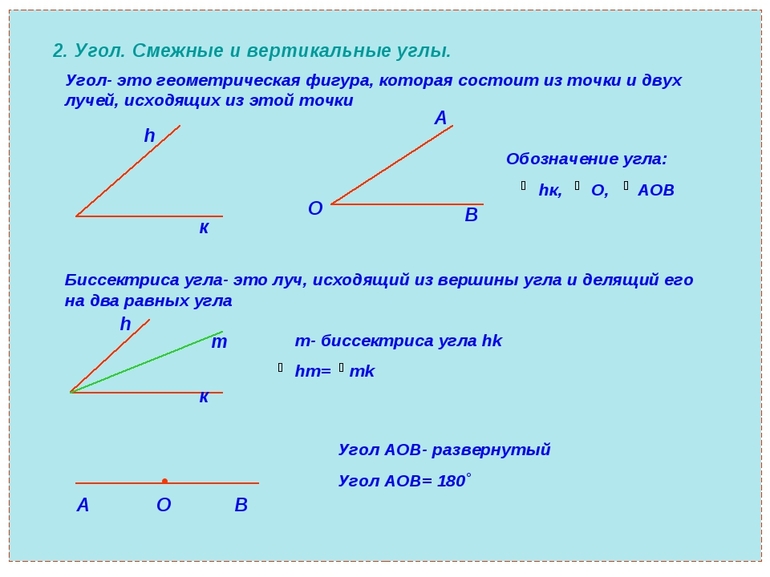
Два луча, выходящие из одной точки, образовывают угол. По сути, это незамкнутая геометрическая фигура. Она имеет вершину (общую точку) и стороны. Обозначают его с помощью трёх заглавных букв, соответствующих трём точкам — вершине и двум лежащим на разных сторонах лучах. Внутренняя часть формируется из множества точек, принадлежащих плоскости, ограниченной сторонами угла.

Существует шесть видов углов:

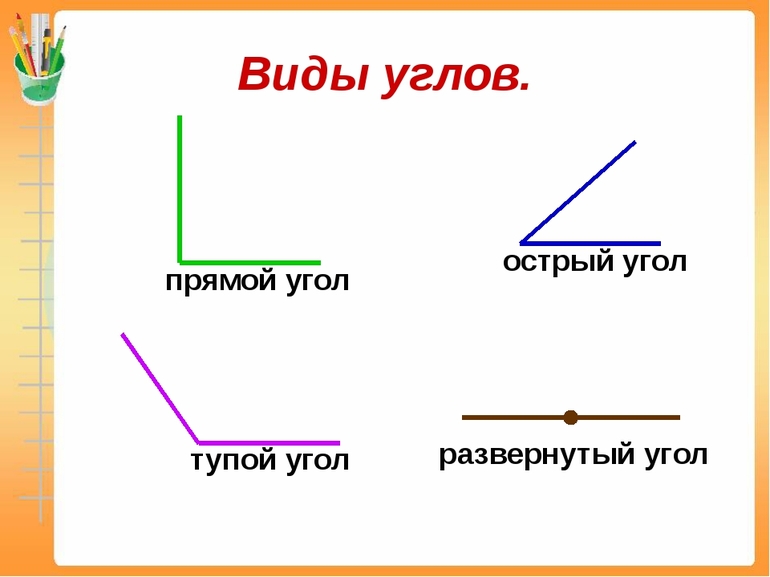
• Острый — расстояние между сторонами составляет меньше 90 градусов.
• Прямой — образовывается двумя взаимно перпендикулярными прямыми.
• Тупой — разворот угла больше 90 градусов, но не превышает 180.
• Развёрнутый — представляет сумму двух прямых элементов.
• Выпуклый — угол между лучами составляет больше 180 градусов, но меньше 360.
• Полный — равняется 360 градусам.

Располагаясь на плоскости, по отношению друг к другу углы могут быть смежными или вертикальными. Согласно определению, смежными углами называют такую пару, у которой одна сторона принадлежит обеим фигурам, а два других луча образуют прямую линию. Вертикальными же считаются углы, стороны которых дополняют друг друга до прямых линий. Они всегда градусно равны.

Единицей измерения разворота фигуры является градусная мера. Если в нём содержится нецелое количество градусов, то используются минуты и секунды. Так, в одном градусе содержится 60 минут, а в одной минуте 60 секунд.

Основные различия между арифметикой и геометрией

1. Арифметика относится к списку чисел или последовательностей, в которых каждое новое и предыдущее числа имеют постоянную разницу. Геометрия относится к списку чисел или последовательностей, в которых каждое новое число и предыдущее число имеют постоянное отношение или кратное.
2. Существует общая разница между двумя числами в арифметической последовательности. В геометрии есть общее отношение между двумя числами.
3.  Новый член может быть получен сложением или вычитанием в арифметической последовательности. В геометрическая последовательность, умножение или деление могут получить новый термин.
4. В арифметике существует линейная вариация терминов. В геометрии существует экспоненциальное изменение терминов.
5. Пример арифметической последовательности — 0, 3, 6, 9, 12, 15. Пример геометрическая последовательность- 3, 9, 27, 81, 6561 гг.
6. Арифметика — это простое манипулирование числами, полезное в повседневной жизни. Геометрия связана со свойствами пространства, связанными с расстоянием, формой, размером и относительным положением объектов или фигур. Это полезно в строительных проектах.

Рекомендации

1. https://link.springer.com/article/10.1007/BF00367686
2. https://books.google.com/books?hl=en&lr=&id=PgHjLgIVidgC&oi=fnd&pg=PR13&dq=arithmetic+and+geometry+mathematics&ots=HsbtfxW4Dx&sig=q3df3gYh3j-7nuppRRj3VWOLL-k

Следствия из теоремы о смежных углах

1. Если два угла равны, то смежные с ними углы равны.
2. Если угол не расширяется, он не равен 180 градусам.
3. Угол, примыкающий к прямому углу (то есть угол, мера которого равна $90^{circ}$), также является прямым углом.
4. Угол, примыкающий к острому углу (значение которого меньше $90^{circle}$), является тупым (больше $90^{circle}$), а к тупому углу — острый.

Пример

Упражнение. Докажите, что у двух неподобных углов смежные с ними углы также неподобны, причем меньшему прилежащему углу соответствует больший угол.

Доказательство. Пусть даны два угла $angle alpha neq angle beta$. Для определенности будем считать, что $angle alpha > angle beta$. Пусть $angle alpha_{1}$ и $angle beta_{1}$ — соответствующие им смежные углы. Тогда по теореме о соседних углах имеем:

$$угол alpha_{1}=180^{circ}-угол alpha, угол beta_{1}=180^{circ}-угол beta$

Так как $angle alpha neq angle beta$, то разности в правой части последних равенств тоже не равны, а если уменьшаемое равно, то разность меньше там, где вычитаемое больше, поэтому $angle alpha_{ 1} < angle beta_{1}$.

КЭД

Смежные углы и их свойства

Смежные углы — соседи, живущие через стенку.

Из свойств лучей нам известно, что вкупе образуют прямую. Таким образом, смежные углы — углы-соседи, «проживающие» на одной прямой. Эта геометрическая особенность подразумевает ряд интересных свойств, одно из которых — связь смежных с развернутыми углами.

Градусная мера смежных углов

Доказательство

Пусть $\angle{ABD}$ и $\angle{DBC}$ — произвольные смежные углы. Докажем, что сумма смежных углов равняется $180^\circ$. Заметим, что луч $BD$ проходит между сторонами развернутого угла $\angle{ABC}$. Градусная мера развернутого угла равняется $180^\circ$.

По $A_8$ мы помним, что градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. Значит:

$$\angle{ABC}=\angle{ABD}+\angle{DBC}=180^\circ$$

Градусная мера смежных углов в сумме составляет $180^\circ$. Что и требовалось доказать.

Задача. Какова градусная мера смежных углов, если про смежные углы известно, что один их них в три раза больше другого?

Решение. Обозначим градусную меру меньшего угла как $x$. Если больший угол больше меньшего в три раза, его градусную меру можно обозначить как $3x$. Сумма смежных углов составляет $180^\circ$. Пользуясь данным свойством, составим следующее уравнение:

$$x+3x=180^\circ$$

Откуда получаем значение меньшего угла $x=45^\circ$. Больший угол по условию больше в три раза и, следовательно, будет равняться $135^\circ$. Градусная мера смежных углов найдена и составляет $45^\circ$ и $135^\circ$.

Ответ: $45^\circ$, $135^\circ$.

{"questions":[{"content":"`speech-1`Разность двух смежных углов равна $40^\\circ$. Найдите градусные меры данных углов. Впишите значения ниже в любом порядке. `input-6``input-16`","widgets":{"speech-1":{"type":"speech","text":"Ваша очередь попробовать посчитать!"},"input-6":{"type":"input","unit":"$^\\circ$","answer":},"input-16":{"type":"input","unit":"$^\\circ$","answer":}},"step":1,"hints":}]}

Сумма смежных углов: следствие из теоремы

Поскольку градусная мера смежных углов в сумме строго определяется как $180^\circ$, это позволяет сделать вывод о том, что если два угла равны, то равны будут и смежные с ними углы. В геометрии бездоказательно выводы приводить нельзя, так что оформим данное наблюдение в виде следствия из теоремы и докажем его.

Итак:

Доказательство

Рассмотрим два равных угла — $\angle{1}$ и $\angle{2}$. Если углы равны, равны их градусные меры. Обозначим градусную меру углов как $x$ и запишем следующее:

$$\begin{cases}\angle{1}=x^\circ\\\angle{2}=x^\circ\end{cases}$$

Сумма смежных углов равняется $180^\circ$. Тогда смежный угол с $\angle{1}$ равен «$180^\circ-x^\circ$». То же самое заключаем про градусную меру угла, смежного с $\angle{2}$: «$180^\circ-x^\circ$». У равных углов $\angle{1}$ и $\angle{2}$ равные смежные углы. Что и требовалось доказать.

{"questions":[{"content":"Градусная мера $\\angle{\\alpha}$, смежного с $\\angle{\\gamma}$, составляет $55^\\circ$. Чему равняется $\\angle{\\beta}$, если известно, что угол, смежный с $\\angle{\\beta}$, по градусной мере равен $\\angle{\\alpha}$?  `input-1`","widgets":{"input-1":{"type":"input","unit":"$^\\circ$","answer":"125"}},"step":1,"hints":["Чтобы не запутаться, определим количество углов, задействованных в задаче. У нас имеется $\\angle{\\alpha}$, $\\angle{\\gamma}$, $\\angle{\\beta}$ и угол, смежный с $\\angle{\\beta}$.  Для простоты обозначим его как $\\angle{\\phi}$.","По условию известно, что $\\angle{\\gamma}$ и $\\angle{\\alpha}$ — смежные углы. Также смежными являются $\\angle{\\beta}$ и $\\angle{\\phi}$.","По следствию из теоремы о сумме смежных углов мы знаем, что у равных углов равны смежные с ними углы.","Если $\\angle{\\phi}=\\angle{\\alpha}=55^\\circ$, то $\\angle{\\gamma}=\\angle{\\beta}=180^\\circ-55^\\circ=125^\\circ$.","Ответ: $125^\\circ$."]}]}

Свойства углов

Рассмотрим свойства углов треугольника:

• против большей стороны лежит больший угол, а также наоборот — против большого угла лежит большая сторона;
• напротив равных сторон располагаются равные углы, а также наоборот — напротив равных углов находятся равные стороны (даже если все углы в равностороннем треугольнике равны);
• сумма углов треугольника равняется 180° (таким образом, каждый угол в равностороннем треугольнике равняется 60°);
• если продолжить одну из сторон треугольника, получится внешний угол;
• любая сторона треугольника будет меньше суммы двух иных сторон, а также больше их разности:a < b+c; a > b−c; b < a+c; b > a−c; c < a+b; c > a−b;
• если две параллельные прямые пересекаются секущей, то соответствующие углы равны;
• две плоскости можно назвать перпендикулярными, если двугранный угол между ними равняется 90°.

Вариант 6

Приветствую всех! Сегодня я хотел бы поделиться своими мыслями о том, как математика оказывает влияние на мою жизнь. Математика – это не только предмет в школе, но и незаменимый инструмент, который помогает мне понимать мир и применять знания в повседневной жизни.

Математика – это язык, с помощью которого мы можем анализировать и описывать различные явления и ситуации. Например, когда я делаю покупки в магазине, мне нужно считать деньги и вычислять сумму покупки, чтобы убедиться, что у меня достаточно денег. Это помогает мне быть ответственным и уметь планировать свои финансы.

Кроме того, математика развивает мое логическое мышление и способность анализировать информацию. Когда я решаю математические задачи, мне приходится использовать различные стратегии и искать паттерны. Эти навыки также помогают мне решать проблемы в других областях жизни, например, при решении задач в науке или при обдумывании стратегий в играх.

Однажды, когда мы с семьей путешествовали, математика пришлась мне очень кстати. Я помогал родителям считать расстояние между городами и время, которое нам потребуется для поездки. Это помогло нам спланировать остановки и определить, сколько времени мы проведем на каждом месте. Благодаря математике наше путешествие прошло гладко и без лишних хлопот.

Математика – это не просто предмет в школе, а мощный инструмент, который помогает нам развивать логическое мышление, аналитические способности и применять знания в повседневной жизни. Она окружает нас повсюду: в науке, в экономике, в путешествиях и даже в играх. Поэтому я считаю, что учиться математике – это необходимость, которая поможет нам успешно справляться с задачами и достигать своих целей. Давайте продолжать развивать свои математические навыки и использовать их для познания мира!

Мне нравится102Не нравится55

Смежные углы – примеры

Пример 1

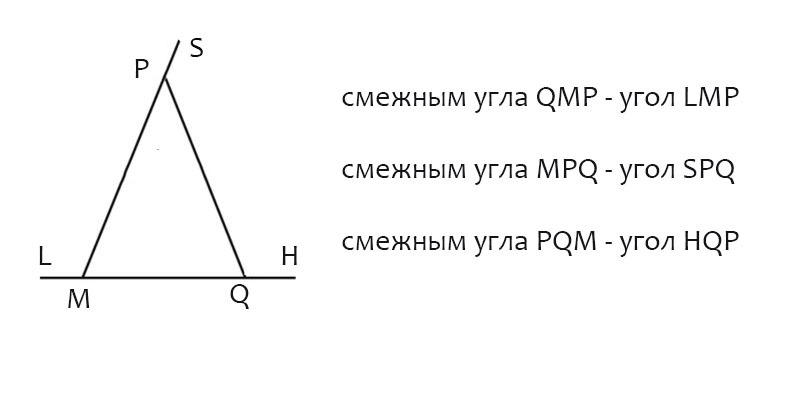
Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.

• Продлим каждую из сторон треугольника прямой.
• Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:

смежным для угла ∠QMP будет ∠LMP,

смежным для угла ∠MPQ будет ∠SPQ,

смежным для угла ∠PQM будет ∠HQP.

Пример 2

Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?

• Два смежных угла в сумме образуют 180°.
• Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.

Пример 3

Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.

• Обозначим величину одного (меньшего) угла через – ∠μ = λ.
• Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
• Исходя из основного свойства смежных углов, μ + η = 180° следует

λ + 3λ = μ + η = 180°,

λ = 180°/4 = 45°.

Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.

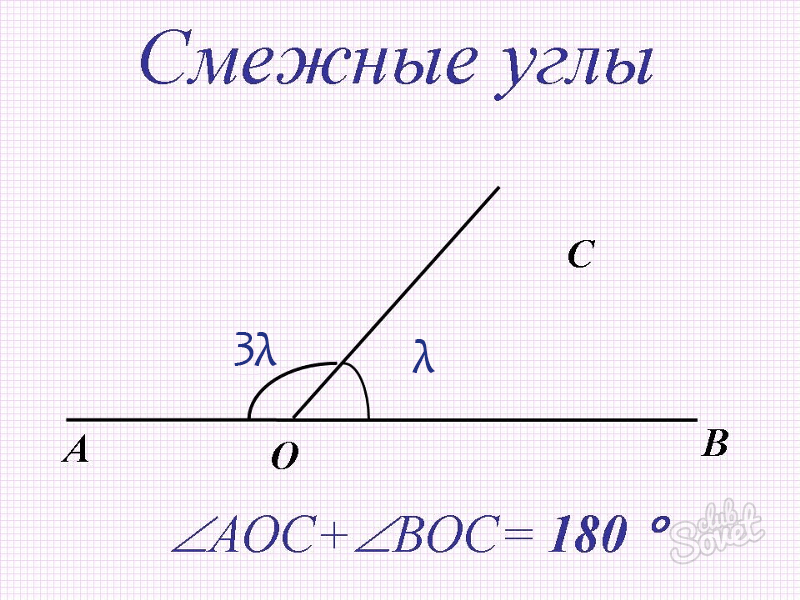
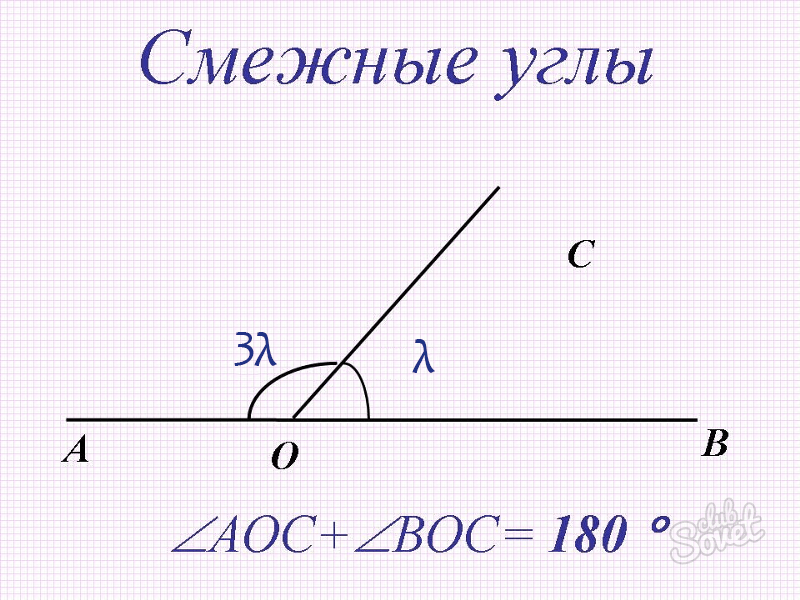
Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.

Как найти смежный угол?

Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.

Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.

Ребёнок не понимает алгебру

Алгебра — это раздел математики, который изучает общие свойства и отношения чисел с использованием переменных и символов. В алгебре мы работаем с неизвестными величинами (переменными), а также с уравнениями, неравенствами, функциями и графиками.

‍

Обучение алгебре начинается обычно в средней школе и продолжается в старших классах. В начальных классах сосредотачиваются на базовых понятиях, таких как переменные, выражения с переменными и уравнения. В старших классах углубляются в системы уравнений, уравнения с параметром и тригонометрию.

‍

Вот несколько советов, которые могут помочь ребёнку лучше понять алгебру.

‍

1. Объясните ребёнку концепцию переменных и их роль в алгебре. Покажите, что переменные представляют неизвестные числа или величины, с которыми мы работаем в уравнениях и выражениях.
2. Введение в алгебру может быть трудным для детей. Разбейте сложные понятия на более простые части и уделите достаточно времени их освоению.
3. Алгебра требует практики. Предоставьте ребёнку возможности для отработки задач и упражнений.
4. Воспользуйтесь  учебниками, онлайн-ресурсами, интерактивными приложениями или видеоуроками, которые предлагают варианты объяснения и примеры по алгебре.
5. Если ребёнок всё ещё испытывает трудности, не стесняйтесь обратиться за помощью к учителям или репетиторам.
6. Поддержите ребёнка и помогите ему поверить в свои силы. Ошибки — это часть процесса.

‍

Определение

Смежные углы – это углы, которые имеют общую вершину и одну общую сторону. Они также называются смежно-вершинными углами. Между двумя смежными углами есть отношение, которое задается их разностью.

Чтобы найти разность смежных углов, необходимо вычесть меньший из углов из большего. Результат будет являться числом, которое указывает на разницу между этими двумя углами.

Например, у нас есть два смежных угла: угол A и угол B. Угол A равен 60 градусов, а угол B равен 45 градусов. Разность смежных углов между ними будет 60 — 45 = 15 градусов.

Разность смежных углов часто используется в геометрии для нахождения дополнительных или смежных углов в различных фигурах. Знание этого понятия помогает понять геометрические свойства и особенности фигур, а также применять его в решении задач и проблем, связанных с углами.

Разность смежных углов — это…

Чтобы найти разность смежных углов, необходимо вычесть значение одного угла от значения другого угла. Результатом будет число, которое указывает на величину разности между этими двумя углами.

Например, если значение одного смежного угла составляет 50 градусов, а значение другого смежного угла равно 30 градусам, то разность между ними будет равна 20 градусам.

Разность смежных углов можно использовать при решении геометрических задач, например, для нахождения значения одного угла по известному значению другого, если известна их разность.

Термин «расстояние смежных углов» — определение и примеры

Для вычисления расстояния смежных углов необходимо знать значения самих углов, а также знать их положение и взаимное расположение. Расстояние может быть как положительным, так и отрицательным, в зависимости от вида конструкции углов.

Примеры:

1. Если имеются два смежных угла равных по величине, то расстояние между ними равно нулю, так как они полностью совпадают.
2. Если имеется два угла, образующих прямую линию, то расстояние между ними будет равно 180 градусов (или π радиан), так как они лежат на противоположных сторонах от прямой.
3. Если имеются два смежных угла, один из которых равен 90 градусов (или π/2 радиан), а другой 45 градусов (или π/4 радиан), то расстояние между ними будет равно 45 градусов (или π/4 радиан), так как они приближены друг к другу и создают угол меньше 180 градусов (или π радиан).

Таким образом, расстояние смежных углов является важной характеристикой геометрических фигур и позволяет оценить их взаимное положение и степень близости или расстояния между ними

Применение в математике

В геометрии разность смежных углов используется для нахождения третьего угла в треугольнике, если известна величина двух других углов. Это значимо для нахождения всех углов треугольника и определения его формы и свойств.

В тригонометрии разность смежных углов используется в формулах, которые позволяют вычислять значения тригонометрических функций. Например, используя разность смежных углов, можно выразить синус или косинус суммы двух углов через синусы и косинусы самих углов.

Кроме того, разность смежных углов важна для решения задач по алгебре и арифметике. Ее использование связано с нахождением разности между двумя углами, а также определением величины одного угла, зная разность и значение другого угла.

Таким образом, понимание и применение понятия разности смежных углов является неотъемлемой частью математического анализа и помогает в решении различных задач в геометрии, тригонометрии, алгебре и арифметике.