Основание треугольника в геометрии: понятие и применение
В геометрии треугольник является одним из самых простых и важных геометрических фигур. Каждый треугольник состоит из трех сторон и трех углов. Существует множество свойств и характеристик треугольников, которые изучаются в геометрии.
Одной из таких характеристик является основание треугольника. Основание треугольника – это одна из его сторон, на которую опущена высота. Она может быть обозначена буквой b. Другими словами, основание треугольника – это любая сторона, на которую проектируется высота. Как правило, основание обозначается буквой a или b.
Примером треугольника с основанием может служить равнобедренный треугольник. В нем две стороны, вершины которых лежат на основании, равны между собой. Также, основание может быть использовано для вычисления площади треугольника по формуле: S = (a x h)/2, где а – основание треугольника, а h – высота, опущенная на это основание.
Что такое основание треугольника?
Основание треугольника является одним из основных понятий геометрии. Этот термин обычно относится к стороне треугольника, которая служит его базой или началом. Основание может быть выбрано из любой из трех сторон треугольника, поскольку каждая из них может быть выбрана в качестве базы. В большинстве случаев, однако, выбирается самая горизонтальная из сторон как основание.
Основание обычно определяется как «противоположная» сторона к высоте, опущенной на третью сторону. Именно это основание, вместе с высотой, позволяет расчет площади треугольника, если они известны. Именно такие смежные понятия могут помочь в решении различных задач, связанных с треугольниками.
В математике и тригонометрии, обычно используется специальный термин «основание угла», отличающийся от понятия основания треугольника. Основание угла является стороной, которая лежит на линии, к которой он относится. Например, угол может иметь основания в виде двух лучей, выходящих из общей точки.
- Пример 1: В треугольнике ABC, сторона AB является прилегающей к углу с чертой на вершине C. Следовательно, AB является «основанием» этого угла.
- Пример 2: В треугольнике DEF, сторона DE является базой. Если опущена высота на сторону DE, то это и будет высотой треугольника, относящейся к этому основанию.
- Пример 3: В прямоугольном треугольнике PQR, гипотенуза PQ имеет два «основания»: PR и QR. При этом, они являются противоположными сторонами к углам, смежным с гипотенузой.
Примеры использования основания треугольника
В геометрии, основание треугольника — это одна из его сторон, которая лежит на основании. Это понятие используется в широком спектре математических и физических приложений.
Вычисление площади
Основание треугольника используется для вычисления его площади. Формула для вычисления площади треугольника:
S = 1/2 * b * h, где b— основание, h — высота, опущенная на это основание. Площадь треугольника можно вычислить, зная длину одной из его сторон и высоту, которая проходит через эту сторону.
Использование основания в тригонометрии
Основание треугольника может быть использовано для определения тригонометрических функций угла наклона. Например, тангенс угла равен отношению стороны, примыкающей к углу, к стороне, лежащей на основании.
Решение геометрических задач
В геометрических задачах основание треугольника используется для нахождения длин других его сторон или углов. Например, если известны длина основания и двух других сторон, можно найти длину третьей стороны, используя теорему Пифагора.
Применение в физике
Основание треугольника применяется в физике, в частности, для вычисления сил векторов. Если известна величина силы и угол, который она образует с горизонтальной плоскостью, то можно определить, сколько этой силы направлено вдоль основания треугольника.
Как найти основание треугольника?
Основание треугольника — это одна из его сторон, к которой проведена высота. Для того, чтобы найти основание треугольника, нужно знать любую другую его сторону и соответствующую высоту.
Пример 1: Дан прямоугольный треугольник ABC, гипотенуза которого равна 10, а катет AC — 6. Найдем основание треугольника:
1. Находим величину второго катета AB по теореме Пифагора:
2. Находим площадь треугольника через произведение стороны на высоту:
S = 0.5 * AC * BG = 0.5 * 6 * 8 = 24
3. Находим высоту треугольника через площадь и основание:
h = 2 * S/AB = 2 * 24/8 = 6
Тогда основание треугольника будет равно AC = 6.
Пример 2: Дан равнобедренный треугольник ABC, в котором боковые стороны равны 8, а высота опущена на основание BC. Найдем основание треугольника:
Основание: определение и роль
Основание имеет ключевое значение в строительстве, инженерии и архитектуре. Оно обеспечивает стабильность и прочность всего сооружения. От качества основания зависит безопасность и долговечность строительных объектов.
Основное назначение основания — перераспределение нагрузки, которую оно получает от сверху на всю подстилающую площадку. Опоры и фундаменты передают нагрузку на основание, и если оно недостаточно крепкое или неравномерное, это может привести к деформации или разрушению сооружения.
Важно отметить, что несущая способность основания должна быть достаточной для поддержки всех нагрузок, включая вес сооружения, окружающие нагрузки (ветер, снег и т.д.) и динамические нагрузки (вибрация, землетрясение и т.д.). При проектировании зданий и сооружений необходимо тщательно анализировать и оценивать свойства основания, включая его геологическую структуру, грунтовую воду, устойчивость к деформациям и многие другие факторы. Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных
Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных
При проектировании зданий и сооружений необходимо тщательно анализировать и оценивать свойства основания, включая его геологическую структуру, грунтовую воду, устойчивость к деформациям и многие другие факторы. Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных.
Кроме того, при проведении строительных работ важно учесть возможные изменения основания в течение времени — например, связанные с периодическими повышениями уровня грунтовых вод или сезонными изменениями грунта
Как найти основание треугольника?
Основание треугольника — это одна из его сторон, на которую опускается перпендикуляр из вершины треугольника. Найти основание треугольника может помочь удобная формула, которая выражает основание через площадь треугольника и высоту, опущенную к этой стороне:
основание = 2 × площадь треугольника / высота, опущенная к этой стороне
Если известна только площадь треугольника и другие стороны, можно воспользоваться формулой Герона для нахождения площади треугольника и затем применить предыдущую формулу для нахождения основания.
Если известна высота треугольника, опущенная к основанию, и одна из других сторон треугольника, можно использовать теорему Пифагора для нахождения оставшейся стороны треугольника. Затем можно использовать формулу для нахождения основания.
Также можно разделить треугольник на два прямоугольных треугольника, используя основание и высоту, и затем применить теорему Пифагора для нахождения других сторон. В этом случае основание будет одним из катетов прямоугольного треугольника.
Для расчета основания треугольника можно также воспользоваться таблицей тригонометрических функций, если угол при основании известен. В этом случае основание будет равно:
основание = сторона, прилежащая к углу при основании / tg(угол при основании)
Площадь и периметр
Площадь и периметр — это две основные характеристики геометрических фигур, которые позволяют определить их размеры и свойства.
Площадь — это мера двумерной площади, занимаемой фигурой на плоскости. Площадь обычно измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и т.д.).
Площадь различных геометрических фигур рассчитывается по-разному:
- Площадь прямоугольника равна произведению длины и ширины: S = a * b, где a и b — длина и ширина соответственно.
- Площадь квадрата равна квадрату его стороны: S = a^2, где a — длина стороны.
- Площадь треугольника может быть рассчитана различными способами, например, по формуле Герона или по формуле «основание на высоту делить на 2».
- Площадь круга равна произведению квадрата радиуса на число Пи: S = π * r^2, где r — радиус круга.
Периметр — это сумма всех сторон фигуры. Периметр также измеряется в единицах длины (метрах, сантиметрах и т.д.).
Периметр различных геометрических фигур рассчитывается по-разному:
- Периметр прямоугольника равен удвоенной сумме длины и ширины: P = 2 * (a + b), где a и b — длина и ширина соответственно.
- Периметр квадрата равен учетверенной длине его стороны: P = 4 * a, где a — длина стороны.
- Периметр треугольника равен сумме длин всех его сторон.
- Периметр круга равен произведению диаметра на число Пи: P = 2 * π * r, где r — радиус круга.
Знание формул для расчета площади и периметра помогает решать задачи на построение и нахождение размеров различных фигур.
Понятие обозначения треугольника в геометрии
В геометрии для обозначения треугольника используются различные символы и обозначения. Наиболее распространенным способом обозначения треугольника является указание вершин треугольника буквами.
Обычно в треугольнике используются заглавные буквы для обозначения вершин. Так, для треугольника ABC вершины обозначаются буквами A, B и C. При этом, вершины обычно указываются в определенном порядке. Например, вершина A может быть указана слева, вершина B – сверху, а вершина C – справа.
Если требуется указать возможные комбинации сторон и углов треугольника, для обозначения используются индексы. Например, сторона AB обозначается как AB, угол ABC обозначается как ∠ABC, а площадь треугольника ABC обозначается как SABC.
Кроме того, существуют и другие способы обозначения треугольника, используемые в специальных случаях или в определенных системах геометрической нотации. Например, в некоторых случаях треугольник может быть обозначен просто через точки, без использования букв или символов. Также, в некоторых текстах используются специальные обозначения для прямоугольных треугольников или треугольников с определенными свойствами.
Призма
Определения:
- Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
- Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
- Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
- Боковая поверхность – объединение боковых граней.
- Полная поверхность – объединение оснований и боковой поверхности.
- Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
- Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
- Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
- Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
- Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
- Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Свойства и формулы для призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:
где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
- Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:
где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1или BB1 и так далее).
Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:
где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.
Виды призм в стереометрии:
- Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
- Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):
где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.
Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:
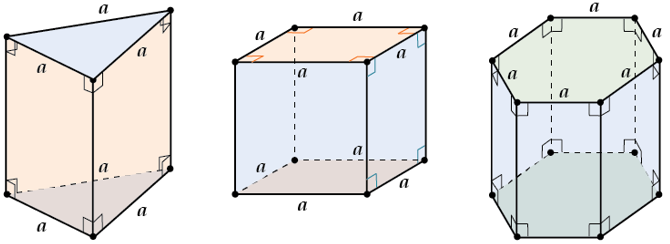
Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.
- Правильная призма является прямой.
Геометрические фигуры
Базовыми фигурами в геометрии на плоскости являются треугольник, четырёхугольник, многоугольник, окружность. В пространстве — это призма, пирамида, сфера, конус.
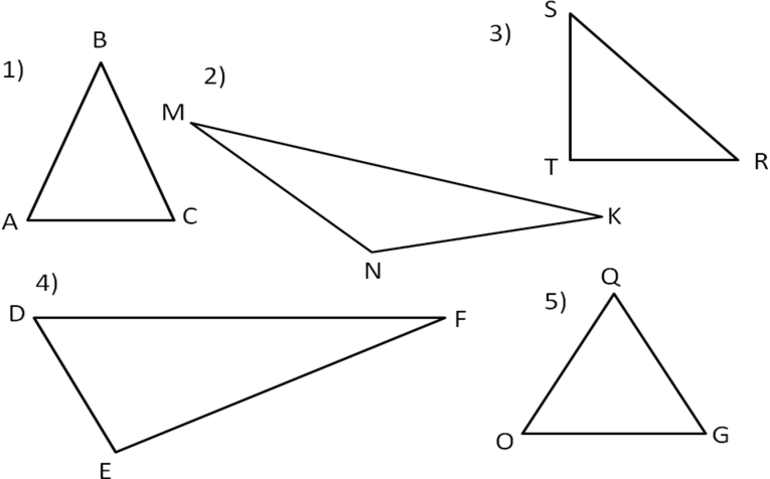
«Треугольник» — простейшая фигура в геометрии, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих вершины треугольника. Отрезки при этом будут называться сторонами треугольника. У треугольника три угла и три стороны. Поэтому можно выделить прямоугольные треугольники (один из углов — прямой), остроугольные треугольники (все углы — острые), тупоугольные треугольники (если один угол тупой). Замечательным свойством треугольника будет формула о сумме его углов, которая равна 180°. Иными словами, если α, β, γ — углы треугольника, то верно равенство α + β + γ =180°.
Треугольник ABC
Если классифицировать треугольники с позиции сторон, то треугольники делятся на равносторонние (все стороны равны), равнобедренные (две стороны из трех равны, но не равны третьей) и произвольные.
В треугольнике против наибольшего угла лежит наибольшая сторона и наоборот.
Огромное значение треугольники играют в геометрии благодаря тому, что почти любая фигура разбивается на треугольники каким-либо методом. Таким образом, чтобы уметь анализировать более сложные фигуры, нужно знать свойства треугольника.
Базовое значение в геометрии играет теорема Пифагора, которая гласит, что в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов: a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}}. Для решения большинства задач в геометрии так или иначе используются теорема Пифагора.
«Четырёхугольник» — фигура, состоящая из четырёх вершин и четырёх отрезков, последовательно соединяющих его вершины, являющихся его сторонами, при этом никакие три вершины не лежат на одной прямой. Последнее требование позволяет исключить вырожденные четырёхугольники, которые представляют собой треугольники или прямые. Важными представителями четырёхугольников являются параллелограмм и трапеция, поскольку почти все остальные четырёхугольники можно анализировать на основе их свойств.
- Параллелограмм — четырёхугольник, у которого противоположные стороны попарно равны и параллельны.
- Трапеция — четырёхугольник, у которого две противоположные стороны параллельны и две другие не параллельны.
Наиболее популярными четырёхугольниками на практике являются квадраты, прямоугольники и ромбы, которые уже определяются на основе параллелограммов.
- Ромб — четырёхугольник, у которого все стороны равны.
- Прямоугольник — четырёхугольник, у которого все углы прямые.
- Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны.
Сфера с радиусом r и диаметром d
Любой многоугольник уже разбивается на вышеописанные фигуры, поэтому его свойства можно изучать на основе рассмотренных фигур. Особняком стоит окружность или круг. Введение понятие «окружности» или «равноудалённости» значительно расширяет функционал и угол зрения геометрической науки. В свою очередь широкое применение круга на практике заставляет геометров пристально изучать свойства окружности, чтобы найденные таким образом закономерности инженеры могли применить в промышленности и других практических областях.
Окружность — это множество точек одной плоскости, равноудаленных от одной точки (центра окружности). При этом расстояние от любой точки окружности до её центра называется радиусом окружности или круга. Термин круг используется, если требуется включить все точки внутри окружности в одну фигуру. Отсюда следует, что окружность в отличие от круга не имеет площади. Но окружность является границей круга.
Если в определении окружности убрать требование на нахождение точек в одной плоскости, то получится сфера или шар.
- Сфера — это множество точек пространства, равноудаленных от одной точки (центра сферы). Сфера является границей шара.
- Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её верхними и нижними основаниями. Наиболее популярной призмой является куб.
- Пирамида — многогранник, основанием которого является многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
- Конус — геометрическая фигура в пространстве, образованная множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).
Призматические многогранники
Призматический многогранник — это обобщение призмы в пространствах размерности 4 и выше. n-мерный призматический многогранник конструируется из двух (n − 1)-мерных многогранников, перенесённых в следующую размерность.
Элементы призматического n-мерного многогранника удваиваются из элементов (n − 1)-мерного многогранника, затем создаются новые элементы следующего уровня.
Возьмём n-мерный многогранник с элементами fi{\displaystyle f_{i}} (i-мерная грань, i = 0, …, n). Призматический (n+1{\displaystyle n+1})-мерный многогранник будет иметь 2fi+f−1{\displaystyle 2f_{i}+f_{-1}} элементов размерности i (при f−1={\displaystyle f_{-1}=0}, fn=1{\displaystyle f_{n}=1}).
По размерностям:
- Берём многоугольник с n вершинами и n сторонами. Получим призму с 2n вершинами, 3n рёбрами и 2+n{\displaystyle 2+n} гранями.
- Берём многогранник с v вершинами, e рёбрами и f гранями. Получаем (4-мерную) призму с 2v вершинами, 2e+v{\displaystyle 2e+v} рёбрами, 2f+e{\displaystyle 2f+e} гранями и 2+f{\displaystyle 2+f} ячейками.
- Берём 4-мерный многогранник с v вершинами, e рёбрами, f гранями и c ячейками. Получаем (5-мерную) призму с 2v вершинами, 2e+v{\displaystyle 2e+v} рёбрами, 2f+e{\displaystyle 2f+e} (2-мерными) гранями, 2c+f{\displaystyle 2c+f} ячейками и 2+c{\displaystyle 2+c} гиперячейками.
Однородные призматические многогранники
Правильный n-многогранник, представленный символом Шлефли {p, q, …, t}, может образовать однородный призматический многогранник размерности (n + 1), представленный прямым произведением двух символов Шлефли: {p, q, …, t}×{}.
По размерностям:
- Призма из 0-мерного многогранника — это отрезок, представленный пустым символом Шлефли {}.
- Призма из 1-мерного многогранника — это прямоугольник, полученный из двух отрезков. Эта призма представляется как произведение символов Шлефли {}×{}. Если призма является квадратом, запись можно сократить: {}×{} = {4}.
Пример: Квадрат, {}×{}, два параллельных отрезка, соединённые двумя другими отрезками, сторонами.
-
многоугольная призма — это 3-мерная призма, полученная из двух многоугольников (один получен параллельным переносом другого), которые связаны прямоугольниками. Из правильного многоугольника {p} можно получить однородную n-угольную призму, представленную произведением {p}×{}. Если p = 4, призма становится кубом: {4}×{} = {4, 3}.
Пример: Пятиугольная призма, {5}×{}, два параллельных пятиугольника связаны пятью прямоугольными сторонами.
- 4-мерная призма, полученная из двух многогранников (один получен параллельным переносом другого), со связывающими 3-мерными призматическими ячейками. Из правильного многогранника {p, q} можно получить однородную 4-мерную призму, представленную произведением {p, q}×{}. Если многогранник является кубом и стороны призмы тоже кубы, призма превращается в тессеракт: {4, 3}×{} = {4, 3, 3}.
Пример: додекаэдральная призма, {5, 3}×{}, два параллельных додекаэдра, соединённых 12 пятиугольными призмами (сторонами).
- …
Призматические многогранники более высоких размерностей также существуют как прямые произведения двух любых многогранников. Размерность призматического многогранника равна произведению размерностей элементов произведения. Первый пример такого произведения существует в 4-мерном пространстве и называется дуопризмами, которые получаются произведением двух многоугольников. Правильные дуопризмы представляются символом {p}×{q}.
| Многоугольник | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |
Общая характеристика
Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.
Основные понятия о составляющих
Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.
Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).
Виды линий:

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.
Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.
Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.
Стандартные объекты
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.
Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.
Виды треугольника в зависимости от угла (У):
Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.
Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.
Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.
Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.
Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.
Использование фигур в ваших проектах
Правильное использование фигур является одним из ключей к успешному графическому дизайну. Форма, цвет, размер и другие характеристики фигур в макете могут определять его настроение и сообщение.
Мягкие, изогнутые и закругленные формы воспринимаются иначе, чем острые угловые формы. Например, компания, чья основная клиентская база — женщины, может использовать круги и кривые в своем логотипе. Аналогичным образом, бизнес в спортивной индустрии будет нуждаться в формах с четкими линиями, которые отображают движение и действия, такие как логотип Nike.
Кроме того, рассмотрите невидимые формы ваших проектов, такие как общий план для веб-сайта или брошюры. Ваш каркас может включать в себя фигуры для заголовка и размещения элементов дизайна, но границы могут не обязательно быть вычерчены или выделены в окончательной конструкции.
- Формы могут быть сгруппированы или использованы в шаблонах, чтобы добавить акцент.
- «Белое пространство» или отрицательное пространство, оставшееся между фигурами, также существенно повлияют на дизайн.
- Эксперименты и изменение форм внутри конструкции могут в конечном итоге привести к желаемому результату.
Треугольник Рёло
Треугольник Рёло — это область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Сам треугольник чем-то напоминает медиатор для гитары и имеет не прямые, а изогнутые грани.
Его ты тоже регулярно встречаешь в обычной жизни. Так, например, треугольник Рёло используют в сфере искусства для уже упомянутых струнных инструментов, а также при рисовании различных диаграмм, где несколько элементов по кругу, сочетаясь между собой, приводят к центральному ядру.
Кроме того, треугольник Рёло — это одна из первых изобретённых человеком форм, так как древние люди, изготавливая свои примитивные орудия труда из камня, нередко обтачивали их именно в такой форме, что позволяло использовать их с любой стороны.
Структура и функции основания призмы
Основание призмы — это одна из ее граней, которая образует поверхность, на которую призма опирается. Основание призмы может быть любой формы: круглым, прямоугольным, треугольным и так далее. Форма и размер основания определяют форму и размер всей призмы.
Функции основания призмы включают несколько аспектов. Во-первых, основание призмы служит опорной точкой для всей структуры призмы. Благодаря своей форме и площади основание обеспечивает стабильность и устойчивость призмы. Основание также является точкой прикрепления других граней призмы.
Во-вторых, основание призмы играет важную роль в определении объема призмы. Объем призмы вычисляется с помощью формулы: V = S * h, где V — объем призмы, S — площадь основания призмы, h — высота призмы. Таким образом, площадь основания прямо пропорциональна объему призмы.
Кроме того, основание призмы может иметь свои уникальные особенности, которые могут быть использованы для определенных целей. Например, если основание призмы является круглым, то призма называется цилиндром. Цилиндр имеет свои характеристики и функции, такие как вместимость или мощность хранения.
Основание призмы также может иметь различные дополнительные элементы, такие как трапециевидные выступы, углубления или волнообразные края. Эти элементы могут использоваться для создания определенных эффектов или улучшения функциональности призмы.
В целом, основание призмы является важной частью ее структуры и определяет ее форму и функциональность. Разнообразие форм и функций основания позволяет использовать призмы в разных областях, таких как геометрия, оптика, физика и промышленность
Практические применения
Строительство:
Знание стороны основания является важным при строительстве зданий и сооружений. Оно позволяет правильно расчертить фундаменты, определить границы строительной площадки и разместить строительное оборудование. Точные измерения стороны основания помогают минимизировать ошибки и повышают качество строительных работ.
Геодезия:
Сторона основания находит свое применение в геодезических работах. Геодезисты используют этот параметр для определения координат точек на местности и создания картографических материалов. Например, при построении топографической карты или при установке геодезических меток, знание стороны основания позволяет правильно определить местоположение объекта.
Инженерные расчеты:
Сторона основания используется в инженерных расчетах для определения площади или объема геометрической фигуры. Например, при проектировании водоема или сборном бассейне, знание стороны основания позволяет правильно определить геометрию конструкции и сделать необходимые расчеты для ее создания.
Машиностроение:
В машиностроении сторона основания применяется для разработки и создания различных деталей и механизмов. Знание этого параметра помогает правильно вычислить размеры и пропорции детали, а также предотвратить возможные деформации или поломки в процессе эксплуатации.
Архитектура:
В архитектуре сторона основания является важным параметром при проектировании зданий и интерьеров. Она позволяет определить пропорции и размеры строения, а также расположение отдельных элементов. Знание этого параметра помогает создавать гармоничные и функциональные архитектурные решения.
Разработка программного обеспечения:
Сторона основания находит применение и в программировании. В разработке программного обеспечения этот параметр может использоваться для определения размеров окна, ширины и высоты интерфейсных элементов и многого другого. Он позволяет создавать пользовательские интерфейсы, которые комфортны для работы и удобны в использовании.



























