Треугольник: формулы и свойства

Треугольник: определение и типы

rticles-content-factoid _nghost-skysmartapp-c338884341 ng-version=»16.2.12″>

ТÑеÑголÑник â геомеÑÑиÑеÑÐºÐ°Ñ ÑигÑÑа, коÑоÑÐ°Ñ ÑоÑÑÐ¾Ð¸Ñ Ð¸Ð· ÑÑÑÑ ÑÑоÑон и ÑÑÑÑ Ð²ÐµÑÑин.

ÐеÑÑÐ¸Ð½Ñ ÑÑеÑголÑника пÑинÑÑо обознаÑаÑÑ Ð·Ð°Ð³Ð»Ð°Ð²Ð½Ñми бÑквами лаÑинÑкого алÑавиÑа. СÑоÑÐ¾Ð½Ñ ÑÑеÑголÑника можно обознаÑиÑÑ ÑеÑез Ð½Ð°Ð·Ð²Ð°Ð½Ð¸Ñ Ð´Ð²ÑÑ Ð²ÐµÑÑин, ÑоÑки коÑоÑÑÑ ÑвлÑÑÑÑÑ Ð½Ð°Ñалом и конÑом оÑÑезка (ÑÑоÑонÑ). ÐÑли же веÑÑÐ¸Ð½Ñ Ð½Ðµ обознаÑенÑ, ÑÑоÑÐ¾Ð½Ñ Ð¼Ð¾Ð¶Ð½Ð¾ запиÑаÑÑ ÑеÑез малÑе бÑÐºÐ²Ñ Ð»Ð°ÑинÑкого алÑавиÑа.

ТÑеÑголÑники бÑваÑÑ ÑÑÑÑ Ð²Ð¸Ð´Ð¾Ð²:

1. ÐÑÑÑоÑголÑнÑе (вÑе ÑглÑ, вÑодÑÑие в ÑоÑÑав, оÑÑÑÑе).

2. ÐÑÑмоÑголÑнÑе (один Ñгол пÑÑмой, Ñавен 90°, оÑÑалÑнÑе оÑÑÑÑе).

3. ТÑпоÑголÑнÑе (один Ñгол ÑÑпой, оÑÑалÑнÑе оÑÑÑÑе).

Также вÑделÑÑÑ ÑавнобедÑеннÑе и ÑавноÑÑоÑонние ÑÑеÑголÑники.

РавноÑÑоÑонний ÑÑеÑголÑник â ÑÑеÑголÑник, вÑе ÑÑоÑÐ¾Ð½Ñ Ð¸ ÑÐ³Ð»Ñ ÐºÐ¾ÑоÑого ÑавнÑ.

РавнобедÑеннÑй ÑÑеÑголÑник â ÑÑеÑголÑник, Ñ ÐºÐ¾ÑоÑого ÑÐ°Ð²Ð½Ñ Ð±Ð¾ÐºÐ¾Ð²Ñе ÑÑоÑÐ¾Ð½Ñ Ð¸ ÑÐ³Ð»Ñ Ð¿Ñи оÑновании.

ÐаÑаÑÑÑÑ Ð² ÑÑÐµÐ±Ð½Ð¸ÐºÐ°Ñ Ð¸ ÑпÑавоÑнÑÑ Ð¼Ð°ÑеÑÐ¸Ð°Ð»Ð°Ñ ÑавнобедÑеннÑе ÑÑеÑголÑники ÑиÑÑÑÑ Ñаким обÑазом, ÑÑо ÑавнÑе боковÑе ÑÑоÑÐ¾Ð½Ñ ÑаÑполагаÑÑÑÑ Ñлева и ÑпÑава, оÑнованием ÑÑиÑаеÑÑÑ Ð½Ð¸Ð¶Ð½ÑÑ ÑÑоÑона. Ðо Ð²Ñ Ð´Ð¾Ð»Ð¶Ð½Ñ Ð¿Ð¾Ð½Ð¸Ð¼Ð°ÑÑ, ÑÑо ÑавнобедÑеннÑй ÑÑеÑголÑник можно легко пеÑевеÑнÑÑÑ, пÑи ÑÑом он не поменÑÐµÑ ÑÐ²Ð¾Ð¸Ñ ÑвойÑÑв. Ðменно поÑÑÐ¾Ð¼Ñ Ð¾Ð¿Ñеделение лÑÑÑе запомниÑÑ Ñак:

РавнобедÑеннÑй ÑÑеÑголÑник â ÑÑеÑголÑник, Ñ ÐºÐ¾ÑоÑого ÑÐ°Ð²Ð½Ñ Ð´Ð²Ðµ ÑÑоÑÐ¾Ð½Ñ Ð¸ ÑглÑ, пÑоÑиволежаÑие ÑÑим ÑÑоÑонам.

637.5K

РавнобедÑеннÑй ÑÑеÑголÑник: ÑвойÑÑва, пÑизнаки и ÑоÑмÑлÑЧиÑаÑÑ â

Пояснение на примерах

В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).

Высотой треугольника называется перпендикуляр, который выходит из вершины треугольника и следует к противоположной стороне (либо к продолжению этой стороны, если треугольник тупоугольный).

В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.

Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.

Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.

Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.

Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:

Уравнение для расчета высоты через площадь:

Найти через длины сторон:

h a = 2 p p — a p — b p — c a

где p — это полупериметр треугольника, который рассчитывается так:

p = a + b + c 2 Можно дать краткую характеристику еще двум способам выразить высоту треугольника:

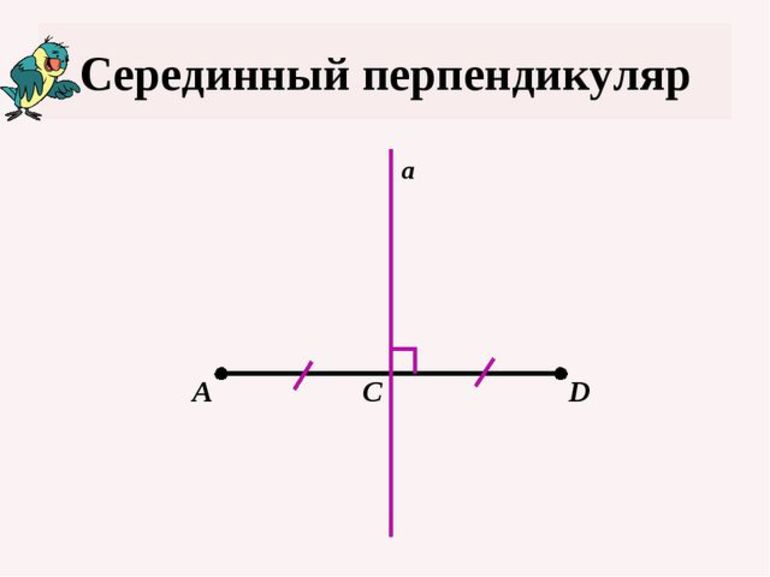
Отрезок (AC) называется перпендикуляром, проведённым из точки (A) прямой (a), если прямые (AC) и (a) перпендикулярны.

Докажем, что от точки (A), не лежащей на прямой (BC), можно провести перпендикуляр к этой прямой.

Отложим от луча (BC) угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне (BC)).

Прямая AA 1 перпендикулярна прямой (BC), а отрезок (AC) является перпендикуляром от точки (A) к прямой (BC).

Если допустить, что через точку (A) можно провести ещё один перпендикуляр к прямой (BC), то он бы находился на прямой, пересекающейся с AA 1 . Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.

Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Поэтому для построения медианы необходимо выполнить следующие действия:1. найти середину стороны;2. соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.

Поэтому для построения биссектрисы необходимо выполнить следующие действия:1. построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части );2. найти точку пересечения биссектрисы угла треугольника с противоположной стороной;3. соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.

Поэтому для построения высоты необходимо выполнить следующие действия:1. провести прямую, содержащую одну из сторон треугольника ( в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике );2. из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней ( перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90 ° ) — это и будет высота.

Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются.

Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.

Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.

Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самым коротким отрезком.

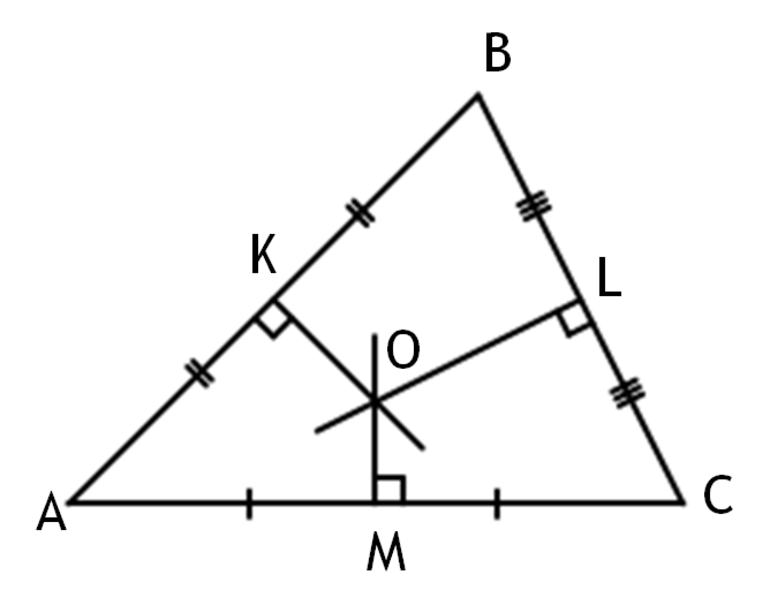
В некоторых случаях необходимо произвести расчеты какого-либо параметра фигуры, но данных бывает недостаточно. В геометрии существует понятие «серединного перпендикуляра». Его значение позволяет легко и быстро находить величины элементов треугольников различных типов. Но перед применением формул следует разобраться в основных свойствах и теоремах.

Основные теоремы

Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.

Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:

• Прямая.
• Обратная.
• Пересечение в треугольнике.

Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.

Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.

Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.

Применение перпендикулярного треугольника

1. Архитектура и строительство: Перпендикулярные треугольники используются для построения прямых линий и определения перпендикулярных направлений при проектировании зданий и сооружений. Например, они помогают строителям создавать углы в 90 градусов и выравнивать стены и полы.
2. Картография: В картографии перпендикулярные треугольники используются для измерения и построения углов при создании карт и планов. Они позволяют прокладывать прямые линии и определять направления с большой точностью.
3. Инженерия: В инженерии перпендикулярные треугольники применяются для выравнивания и установки оборудования. Они помогают определить точные углы и направления, необходимые для правильной установки и функционирования различных систем и механизмов.
4. Геодезия: В геодезии перпендикулярные треугольники используются для измерения и построения прямых линий при определении географических координат и создании геодезических сетей.
5. Математика: В математике перпендикулярные треугольники раскрывают различные свойства и законы геометрии. Они являются базовым понятием в изучении теорем о прямых углах, прямых линиях и ортогональных направлениях.

Это лишь несколько примеров применения перпендикулярного треугольника. Это геометрическое понятие имеет широкий спектр применений и используется во многих областях науки, техники и дизайна.

Формулы площади треугольника

1.Произвольный треугольник – формулы площади

a, b, c — стороны; α — угол между сторонами a и b; p=(a+b+c) / 2— полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h_a — высота, проведенная к стороне a.

1. S=(1/2)*(a* h_a) – по стороне и высоте.
2. S=(1/2) *(a*b*sinα) по двум сторонам и синусу угла между ними
3. Прямоугольный треугольник – площадь

   a, b — катеты; c — гипотенуза; h_c — высота, проведенная к стороне c.

   Примечание – в прямоугольном треугольнике:

   – Синус α – это отношение AB/OB (отношение противолежащего катета к гипотенузе)

   – Косинус α – это отношение ОА/OB (отношение прилежащего катета к гипотенузе)

   – Тангенс α – это отношение AB/OA (отношение противолежащего катета к прилежащему)

   – Котангенс α – это отношение ОА/AB (отношение прилежащего катета к противолежащему)

   “>

Важные свойства

Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:

В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.

Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:

Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:

Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.

Ортоцентр треугольника

      Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.

      Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, противолежащей стороне (рис.3).

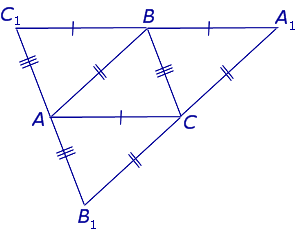
Рис.3

      Обозначим точки пересечения этих прямых символами A₁, B₁ и C₁, как показано на рисунке 3.

      В силу параллельности прямых AC и C₁A₁, а также BC и C₁B₁ четырёхугольники   AC₁BC   и   ABA₁C – , откуда

C₁B = AC = BA₁.

      Следовательно, точка B является серединой стороны C₁A₁.

      В силу параллельности прямых BC и C₁B₁, а также AB и B₁A₁ четырёхугольники   AC₁BC   и   ABCB₁ – ,, откуда

C₁A = BC = A₁B₁.

      Следовательно, точка A является серединой стороны C₁B₁.

      В силу параллельности прямых AB и B₁A₁, а также AC и C₁A₁ четырёхугольники   ABA₁C   и   ABCB₁ – , откуда

A₁C = AB = B₁C.

      Следовательно, точка C является серединой стороны B₁A₁.

      Таким образом, высоты треугольника ABC являются треугольника A₁B₁C₁ (рис. 4),

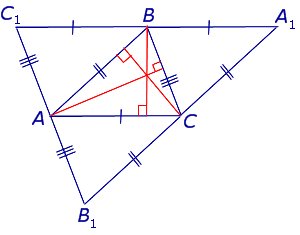
Рис.4

и в силу пересекаются в одной точке.

      Теорема 1 доказана.

      Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.

      У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.

Теорема о перпендикулярных прямых и ее доказательство

Теорема о перпендикулярных прямых
Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

«Кто это вообще придумал?», — можете возразить вы. «Почему мы должны этому верить? Вдруг все иначе, а нас обманывают». Если это так, то ваши опасения — показатель пытливости ума!

Что такое теорема? Это утверждение, нуждающееся в доказательстве. Это означает, что его не принимает на веру никто: ни вы, ни учитель, ни самый великий ученый. Есть много способов доказательства теорем, один из которых — метод от противного. Используя его, мы будто соглашаемся с противоположным заявлением и рассуждаем, что из этого последует.

Например, попробуем доказать утверждение «осенью грачи улетают на юг» методом от противного. Предположим, что грачи остаются зимовать в наших городах. Тогда мы должны видеть их осенью и зимой повсеместно, а в небе не должно быть видно признаков масштабного перелета. Так ли это на самом деле? Конечно же, нет.

Теперь с помощью этого метода попробуем доказать теорему о перпендикулярных прямых.

Предположим, что теорема ложна, а значит, через точку, лежащую на прямой, можно провести несколько перпендикулярных прямых.

Проверим гипотезу:

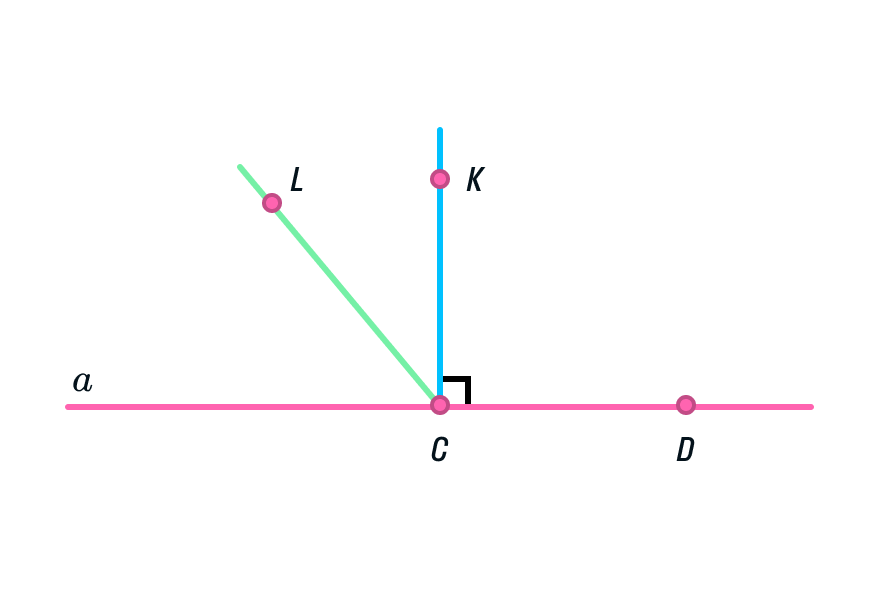
1. Возьмем линейку и проведем прямую а, отметив на ней точки С и D.

2. Далее построим перпендикулярную прямую из точки С. Угол КСD равен 90°.

3. Отрезок КС находится на прямой, перпендикулярной а.

4. Предположим, что есть еще одна прямая, перпендикулярная а. Проведем ее через точку С и отметим на ней точку L.

5. Тогда угол LCD равен 90° и угол КСD равен 90°.

6. Пункт номер 5 невозможен: от отрезка CD можно отложить только один прямой угол в данной плоскости.

7. А значит, через точку С можно провести только одну прямую, перпендикулярную прямой а.

Что и требовалось доказать: вы — молодцы!

Фигуры с перпендикулярными прямыми

Одной из первых фигур, с которыми знакомится человек, являются квадрат и прямоугольник.

Прямые углы приятны человеческому взгляду, поэтому очень часто квадрат или прямоугольник используют как форму для столешниц, стульев, тумбочек и других предметов. Весь окружающий человека мир составлен из параллельных и перпендикулярных линий.

Рис. 2. Квадрат.

Еще со времен Древней Греции известен прямоугольный треугольник. Форму прямоугольного треугольника принимали различные приборы для навигации, кроме того, много времени изучению свойств прямоугольного треугольника уделил Пифагор. Именно его авторству принадлежит Теорема Пифагора, которая часто востребована в решениях задач.

Существует прямоугольная трапеция, у которой одна из сторон перпендикулярна обоим основанием. А стереометрия и вовсе пестрит перпендикулярами в пространстве: правильная призма, прямоугольная пирамида и самый обычный куб.

К тому же, в любом треугольнике можно провести высоту, что необходимо для нахождения площади фигуры. Перпендикуляр для нахождения площади пригодится и в параллелограмме, а прямоугольный треугольник и квадрат имеют высоту в составе своих сторон, из-за чего площадь этих фигур гораздо проще найти.

Рис. 3. Высота.

Что мы узнали?

Мы разобрали, что такое перпендикулярные прямые, поговорили о свойствах перпендикуляров и описали фигуры, для построения которых необходимы перпендикулярные прямые. Разобрались в теме для полного понимания при первой встрече с данным вопросом в 6 классе.

1. /5

   Вопрос 1 из 5

   Чтобы отрезки назывались перпендикулярными, должно выполняться два условия:

   • отрезки должны пересекаться, а угол пересечения между ними должен равняться 90 градусов
   • отрезки должны быть параллельными, а угол между ними должен равняться 90 градусов
   • отрезки должны пересекаться, а угол пересечения между ними должен равняться 180 градусов
   • отрезки должны быть параллельны, а односторонние углы между ними должны равняться 180 градусов

Пояснение на примерах

В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).

В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.

Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.

Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.

Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.

Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:

Уравнение для расчета высоты через площадь:

Найти через длины сторон:

где p — это полупериметр треугольника, который рассчитывается так:

Можно дать краткую характеристику еще двум способам выразить высоту треугольника:

4. Через длину прилежащей стороны и синус угла

5. Через стороны и радиус описанной окружности

Математика. 3 класс

Конспект урока

Виды треугольников по видам углов. Закрепление изученного материала

Перечень вопросов, рассматриваемых в теме:

Какие виды треугольников различают по видам углов?

Как различать треугольники: прямоугольный, тупоугольный, остроугольный?

Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.

Виды треугольников по величине углов

Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.

Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.

Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.

Основная и дополнительная литература:

1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 85-87.

2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.

3. Рудницкая В. Н. Математика. Дидактические материалы. ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что вы уже знаете о видах треугольников.

По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.

Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон. Ведь у каждого есть ещё и по три угла.

У вас уже появились идеи?

Острые – меньше прямого

Прямые – угол 90 градусов

Тупые – больше прямого

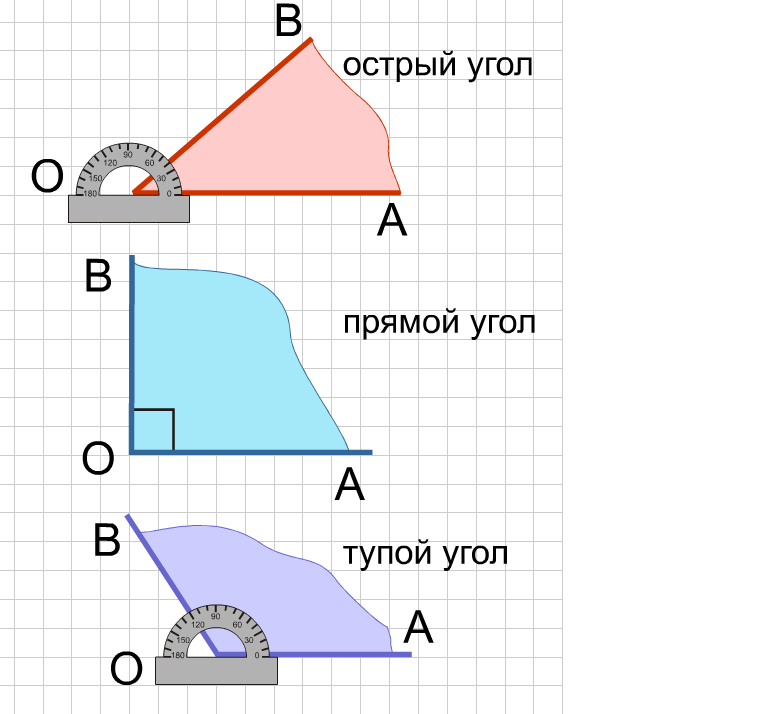
Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:

те, у которых все углы острые, – остроугольные,

те, у которых есть прямой угол, – прямоугольные,

те, у которых есть тупой угол, – тупоугольные.

Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.

Обычно вид треугольника можно определить на глаз.

Попробуйте определить виды треугольников по величине углов без измерений.

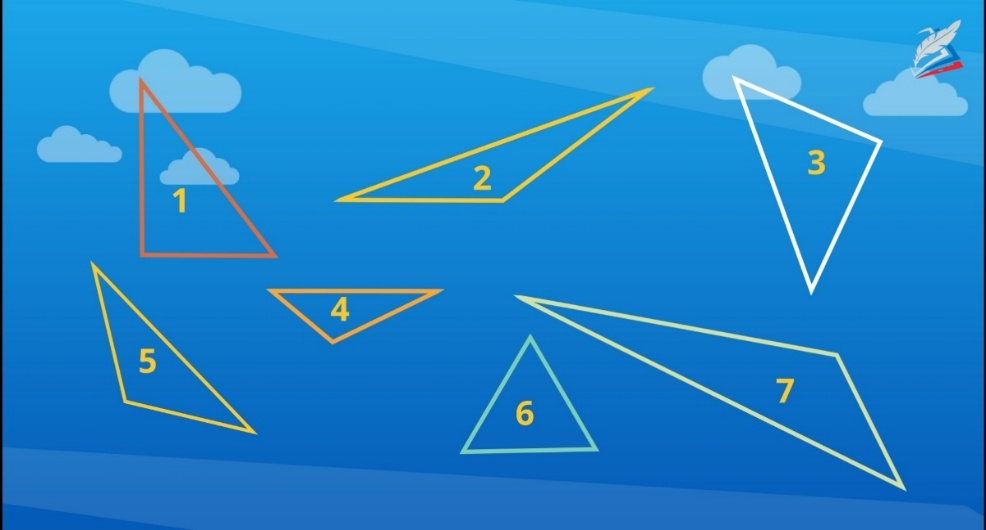
тупоугольный– 2, 4, 7, 5

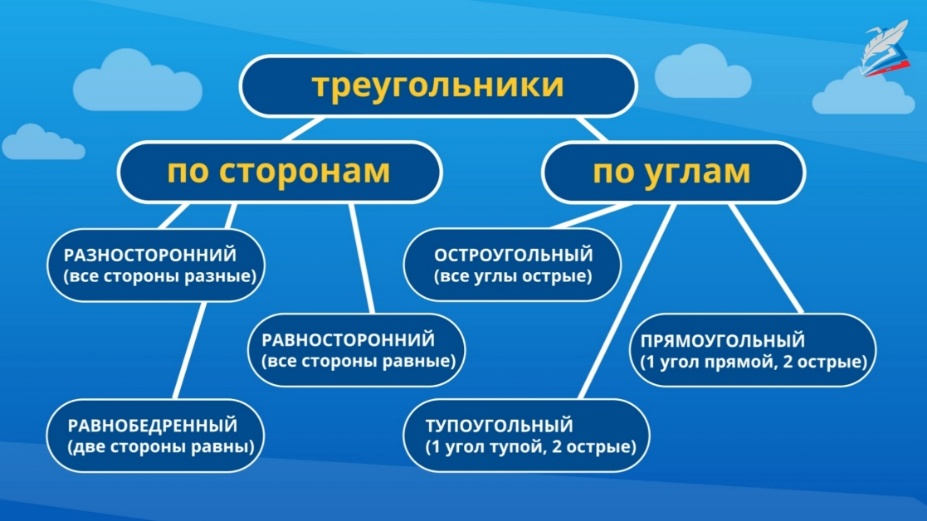
По величине углов различают 3 вида треугольников:

Остроугольные, прямоугольные и тупоугольные

Определить вид треугольника можно тремя способами:

с помощью измерений, на глаз и по условным обозначениям.

Задания тренировочного модуля

Остроугольный треугольник – это треугольник, у которого ……………………

Прямоугольный треугольник – это треугольник, у которого есть ……………………

Тупоугольный треугольник – треугольник, все стороны которого есть ……………………

Правильные варианты ответов:

Остроугольный треугольник — это треугольник, у которого все углы острые.

Прямоугольный треугольник — это треугольник, у которого есть прямой угол.

Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.

Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:

Теорема о взаимно перпендикулярных сторонах треугольника и ее доказательство

Теорема о взаимно перпендикулярных сторонах треугольника утверждает, что если к высоте, опущенной из вершины треугольника на одну сторону, провести биссектрису, опущенную из другой вершины на противоположную сторону, то эти две линии пересекаются под прямым углом.

Доказательство этой теоремы основано на использовании косинусов и биссектрис в треугольнике:

1. Пусть ABC — треугольник, AC и BC — взаимно перпендикулярные стороны, H — точка пересечения высот, BD — биссектриса угла B.
2. Так как AC и BC взаимно перпендикулярны, то AC является основанием прямоугольного треугольника ABC.
3. По определению биссектрисы AD/DC = AB/BC.
4. По теореме косинусов в треугольнике ABC: cosA = BC/AB, cosB = AC/AB.
5. Из пункта 3 следует, что AD/DC = cosB/cosA.
6. Умножим обе части на DC: AD = DC * cosB/cosA.
7. В прямоугольном треугольнике AHD: sinB = AD/AH, cosA = AH/AC.
8. Из пунктов 6 и 7 следует, что sinB/cosA = DC * cosB/AH.
9. В прямоугольном треугольнике BHD: sinA = BD/BH, cosB = BH/BC.
10. Из пунктов 8 и 9 следует, что sinA/cosB = DC * cosA/BC.
11. Поскольку sinB/cosA = cosB/sinA, то DC * cosB/AH = DC * cosA/BC.
12. Отсюда следует, что AH = BH и BD

Свойства

• Задача Фаньяно. Ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.
• Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
• Если точки A₁, B₁ и C₁ на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

∠BA1C1=∠CA1B1{\displaystyle \angle BA_{1}C_{1}=\angle CA_{1}B_{1}} , ∠CB1A1=∠AB1C1{\displaystyle \angle CB_{1}A_{1}=\angle AB_{1}C_{1}} и ∠AC1B1=∠BC1A1{\displaystyle \angle AC_{1}B_{1}=\angle BC_{1}A_{1}},

то A1B1C1{\displaystyle A_{1}B_{1}C_{1}} — ортотреугольник треугольника ABC.

Если вокруг данного остроугольного треугольника описать окружность и в трех вершинах треугольника провести прямые, касательные к окружности, то пересечение этих прямых образует треугольник, который называют тангенциальным треугольником по отношению к данному треугольнику.

Свойства подобия родственных треугольников

Исходный треугольник ΔABC{\displaystyle \Delta ABC} по отношению к ортотреугольнику является треугольником трех внешних биссектрис.

△A1B1C1{\displaystyle \triangle A_{1}B_{1}C_{1}} — ортотреугольник треугольника △ABC{\displaystyle \triangle ABC}, а △A2B2C2{\displaystyle \triangle A_{2}B_{2}C_{2}}— треугольник Жергонна ортотреугольника. H{\displaystyle H}— ортоцентр △ABC{\displaystyle \triangle ABC}, инцентр △A1B1C1{\displaystyle \triangle A_{1}B_{1}C_{1}}и центр описанной окружности △A2B2C2{\displaystyle \triangle A_{2}B_{2}C_{2}}. Треугольники △ABC{\displaystyle \triangle ABC} и △A2B2C2{\displaystyle \triangle A_{2}B_{2}C_{2}} подобны.

• Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
• Треугольник Жергонна ортотреугольника и исходный треугольник подобны (см. рисунок).
• Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
• Ортотреугольник треугольника Жергонна и исходный треугольник подобны.
• Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности (антипараллельности) сторон родственных треугольников.

Свойства параллельности (антипараллельности) сторон родственных треугольников

• Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
• Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
• Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
• Если точки касания вписанной в данный треугольник окружности соединены отрезками, то получится треугольник Жергонна. Пусть в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно, ортотреугольник треугольника Жергонна и исходный треугольник подобны.

Другие свойства

Площадь ортотреугольника равна:

Sort=S(2abc)2(a2+b2−c2)(a2+c2−b2)(b2+c2−a2){\displaystyle S_{ort}={\frac {S}{(2abc)^{2}}}(a^{2}+b^{2}-c^{2})(a^{2}+c^{2}-b^{2})(b^{2}+c^{2}-a^{2})}

где S{\displaystyle S} — площадь треугольника ΔABC; a,b,c{\displaystyle a,b,c} — его соответствующие стороны.

• Окружность, описанная около ортотреугольника Δabc, для самого треугольника ΔABC является окружностью Эйлера (окружностью 9 точек), то есть одновременно проходит, через 3 основания медиан последнего. Заметим, что эти 3 основания медиан являются вершинами дополнительного треугольника для треугольника ΔABC.
• Радиусы окружности, описанной около данного треугольника ΔABC, проведенные через его вершины, перпендикулярны соответственным сторонам ортотреугольника Δabc (Зетель, следствие 2, § 66, с. 81).

Пример решения задачи

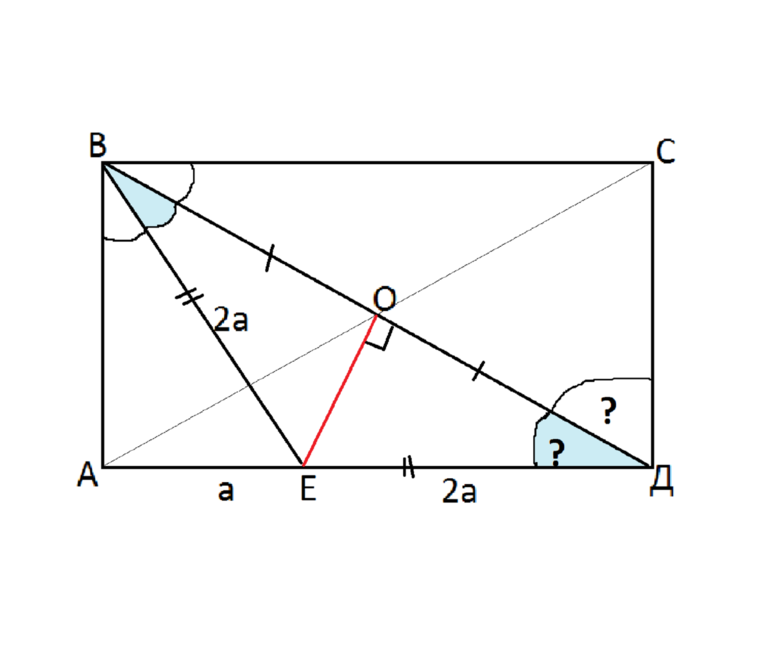
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

1. Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
2. Серединный перпендикуляр, проведенный к диагонали прямоугольника.
3. Точка Е делит сторону на отрезки а и 2а.

Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении

Рисунок 1. Чертеж для решения задачи.

Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:

Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
Необходимо найти угол ЕВО. Сделать это проблемно

Рекомендуется обратить внимание на треугольник АВЕ.
При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
Угол СВЕ вычисляется следующим образом: 90 — 30 = 60 (градусов).
Следовательно, искомый угол равен 30, поскольку 90 — 30 — 30 = 30.
В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).. Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой «х»

Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = ^(1/2) = a * ^(1/2). Следовательно, АВ = a * ^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 — d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 — (d^2) / 4]^(1/2).

Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой «х». Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = ^(1/2) = a * ^(1/2). Следовательно, АВ = a * ^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 — d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 — (d^2) / 4]^(1/2).

Задача Фаньяно

      Задача Фаньяно. Рассматриваются всевозможные треугольники   DEF,   вершины    D,   E   и   F   которых лежат на сторонах   BC,   AC и   AB     ABC   соответственно. Доказать, что из всех треугольников DEF наименьшим  обладает ортоцентрический треугольник треугольника   ABC.

      Решение. Пусть   DEF – один из рассматриваемых треугольников. Обозначим символом   D₁   точку, , и обозначим символом   D₂   точку,  (рис.8).

Рис.8

      Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D₁D₂. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D₁D₂ с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D₁D₂ (рис.9).

Рис.9

      Заметим также, что выполнено равенство

AD = AD₁ = AD₂.

      Кроме того, выполнено равенство

      Поэтому

      Отсюда вытекает, что длина отрезка D₁D₂ будет наименьшей тогда, когда длина отрезка AD  будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF  треугольник с наименьшим периметром является единственным.

      Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус буквами h, c и R соответственно, то, воспользовавшись , получим:

      Следовательно, наименьший периметр рассматриваемых треугольников DEF равен

      Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.

      Лемма. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).

Рис.10

      В этом случае отрезок D₁D₂  проходит через точки F и E.

      Доказательство. Заметим, что в силу выполняются равенства:

      Кроме того, в силу DFK и KFD₂, а также в силу DEL и LED₁ выполняются равенства:

      Следовательно,

откуда вытекает, что углы AEF и D₁EL , а также AFE и D₂FK являются . Это означает, что точки D₁, F, E, D₂ лежат на одной прямой. Лемма доказана.

      Доказательство леммы и завершает решение задачи Фаньяно.

Прямоугольный треугольник и теорема Пифагора

article>СÑоÑÐ¾Ð½Ñ Ð² пÑÑмоÑголÑном ÑÑеÑголÑнике назÑваÑÑÑÑ Ð¿Ð¾-оÑобенномÑ. Так, ÑÑоÑона, лежаÑÐ°Ñ Ð½Ð°Ð¿ÑоÑив пÑÑмого Ñгла, назÑваеÑÑÑ Ð³Ð¸Ð¿Ð¾ÑенÑзой, она ÑÐ°Ð¼Ð°Ñ Ð±Ð¾Ð»ÑÑаÑ. Ðве дÑÑгие ÑÑоÑÐ¾Ð½Ñ â каÑеÑÑ. ÐÐµÐ¶Ð´Ñ Ð½Ð¸Ð¼Ð¸ ÑÑÑеÑÑвÑÐµÑ ÑооÑноÑение, именÑемое ÑеоÑемой ÐиÑагоÑа.

ÐажнÑе ÑвойÑÑва:

• каÑеÑ, лежаÑий напÑоÑив Ñгла 30°, Ñавен половине гипоÑенÑзÑ;

• в ÑавнобедÑенном пÑÑмоÑголÑном ÑÑеÑголÑнике оÑÑÑÑе ÑÐ³Ð»Ñ ÑÐ°Ð²Ð½Ñ 45°.