Свойства
Построение биссектрисы
Свойства точек пересечения биссектрис
- Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
- Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
- Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
- Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.
Свойства, связанные с углами
- Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
- Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
- Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.
Свойства биссектрис равнобедренного треугольника
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
- В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
- Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный.
- У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
- У равностороннего треугольника все три внутренние биссектрисы равны.
Свойства оснований биссектрис
Точка пересечения биссектрисы со стороной треугольника называется основанием биссектрисы.
BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.
- Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.
- Теорема о биссектрисе — частный случай теоремы Штейнера.
- Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
- Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
- Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
- Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .
Свойства осей биссектрис
- Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
- Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.
Другие свойства
- Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Расстояния от сторон угла до любой точки биссектрисы одинаковы.
- Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора.
- Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника.
Биссектриса и параллельность, биссектрисы смежных углов
Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например,
Случай 1
Здорово, правда? Давай поймём, почему так.
С одной стороны, — мы же проводим биссектрису!
Но, с другой стороны, — как накрест лежащие углы (вспоминаем тему ).
И теперь выходит, что; выкидываем середину: ! — равнобедренный!
Случай 2
Представь треугольник (или посмотри на картинку)
Давай продолжим сторону за точку. Теперь получилось два угла:
- — внутренний угол
- — внешний угол — он же снаружи, верно?
Так вот, а теперь кому-то захотелось провести не одну, а сразу две биссектрисы: и для, и для. Что же получится?
А получится прямоугольный!
Удивительно, но это именно так.
Разбираемся.
Как ты думаешь, чему равна сумма?
Конечно же, — ведь они все вместе составляют такой угол, что получается прямая.
А теперь вспомним, что и -биссектрисы и увидим, что внутри угла находится ровно половина
от суммы всех четырех углов: и — — то есть ровно. Можно написать и уравнением:
Итак, невероятно, но факт:
Угол между биссектрисами внутреннего и внешнего угла треугольника равен.
Случай 3
Видишь, что здесь все так же, как и для внутреннего и внешнего углов?
Или ещё раз подумаем, почему так получается?
Снова, как и для смежных углов,
(как соответственные при параллельных основаниях).
И опять, составляют ровно половину
от суммы
Вывод:
Если в задаче встретились биссектрисы смежных
углов или биссектрисы соответственных
углов параллелограмма или трапеции, то в этой задаче непременно
участвует прямоугольный треугольник, а может даже и целый прямоугольник.
Биссектрисы двух секущих
Биссектрисы пары прямых пересекаются по определению биссектрис четырех угловых секторов, определяемых двумя прямыми. Строго говоря, есть четыре биссектрисы для двух прямых, если мы придерживаемся первого определения биссектрисы. Во время доказательства следующей теоремы мы покажем, что эти четыре биссектрисы несут две прямые, которые мы назовем биссектрисами секущих .
- Уравнение биссектрис: если в ортонормированной системе координат, то уравнения секущих соответственно равны
- ax + by + c = 0 и a’x + b’y + c ‘= 0, тогда уравнения их биссектрис:
- вИкс+бy+противв2+б2знак равно±в′Икс+б′y+против′в′2+б′2{\ displaystyle {\ frac {ax + by + c} {\ sqrt {a ^ {2} + b ^ {2}}}} = \ pm {\ frac {a’x + b’y + c ‘} { \ sqrt {а ‘^ {2} + Ь’ ^ {2}}}}}
Теорема — Биссектрисы пары секущих перпендикулярны.
Демонстрация
Обозначим через (zx) и (ty) две прямые. Они пересекаются в точке О. Мы называем:
- [Или) биссектриса xOy;
- [Или ‘) биссектриса zOt;
- [Ov) биссектриса yOz;
- [Ov ‘) биссектриса tOx.
- Углы xOy и zOt в вершине противоположны. Следовательно, они равны. Следовательно, углы xOu = 1/2 xOy и zOu ‘= 1/2 zOt также равны. Поскольку [Ox) и [Oz) переносятся одной линией, то же самое касается [Ou) и [Ou ‘) »(мы также использовали тот факт, что [Ou’) нарисован в секторе zOt). То же самое и с другими парами биссектрис.
- По предположению, углы zOy и yOx дополнительные: zOy + yOx = 180 °. Итак, uOv = uOy + yOv = 1/2 xOy + 1/2 yOz = 1/2 (xOy + yOz) = 180 ° / 2 = 90 °. CQFD
Биссектрисы как оси симметрии D и D ‘. — Если u и v — два единичных вектора, направляющие D и D ‘соответственно, тогда u + v и uv направляют оси симметрии объединения D u D’ (нарисуйте ромбы) .
Таким образом, мы получаем понятие биссектрисы двух секущих аффинных прямых, не переходя наивную точку зрения на геометрические углы. Скалярное произведение (u + v). (Uv) равно нулю, поскольку u и v унитарны: две биссектрисы ортогональны.
Биссектрисы двух прямых и гармонических лучей —
- Если D и D ‘- две секущие линии и , — их биссектрисы, то D, D’ и образуют гармонический пучок .Δ{\ displaystyle \ Delta \,}Δ′{\ displaystyle \ Delta ‘\,}Δ{\ displaystyle \ Delta \,}Δ′{\ displaystyle \ Delta ‘\,}
- Если D, D ‘ и образуют гармонический луч и если и перпендикулярны, то и являются биссектрисами D и D’Δ{\ displaystyle \ Delta \,}Δ′{\ displaystyle \ Delta ‘\,}Δ{\ displaystyle \ Delta \,}Δ′{\ displaystyle \ Delta ‘\,}Δ{\ displaystyle \ Delta \,}Δ′{\ displaystyle \ Delta ‘\,}
Please enable JavaScript.
Coggle requires JavaScript to display documents.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые…
- Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой
- Виды треугольников
- По углам
Признаки равенства прямоугольных треугольников
По двум катетам
По катету и острому углу
По гипотенузе и острому углу
По гипотенузе и катету
Свойства:
Сумма острых углов прямоугольного треугольника равна 90˚.
Катет, противолежащий углу в 30˚, равен половине гипотенузы.
Теорема Пифагора квадрат гипотенузы равен сумме квадратов катетов.
Центр описанной окружности – есть середина гипотенузы.
Радиус R описанной окружности есть половина гипотенузы
Медиана, проведенная к гипотенузе, равна ее половине
Тригонометрические свойства
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
По сторонам
Углы равнобедренного треугольника, прилежащие к основанию, равны.
Биссектриса, медиана и высота, проведенные к основанию, совпадают.
Биссектриса, медиана и высота, проведенные из одной вершины, совпадают.
Равносторонний треугольник имеет центр — точка пересечения биссектрис, медиан, высот, центр описанной и вписанной окружностей.
Равные треугольники: Треугольники называют равными, если у них соответствующие стороны и углы равны
1 признак: По двум сторонам и углу между ними
2 признак: По стороне и двум прилежащим к ней углам
3 признак: По трем сторонам
Подобные треугольники — треугольники, углы у которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
1 признак: по двум пропорциональным сторонам и углу между ними
2 признак:по двум углам
3 признак: по трем пропорциональным сторонам
Замечательные линии треугольника
Биссектриса — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне.
Все три биссектрисы треугольника пересекаются в одной точке.
Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам:
Высота — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника.
Если AH и BM — прямые, содержащие высоты AH и BM треугольника ABC, то треугольники CHM и CAB подобны, коэффициент подобия равен модулю косинуса угла C.
Медиана- это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Все медианы треугольника пересекаются в одной точке, называемой центроидом (центром тяжести) треугольника
В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины: AO:OA1=BO:OB1=CO:OC1=2:1
Теорема косинусов квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Теорема синусов стороны треугольника пропорциональны синусам противолежащих углов.
Площадь треугольника
Формула Герона
Средняя линия треугольника- это отрезок, соединяющий середины двух его сторон.
Высоты треугольника
Высота треугольника — перпендикуляр, проведённый из вершины угла к противолежащей стороне (или прямой, содержащей противоположную сторону).
Странное определение, правда? Чуть ниже расскажем, почему оно справедливо.
Чаще всего высоту обозначают буквой h (H).
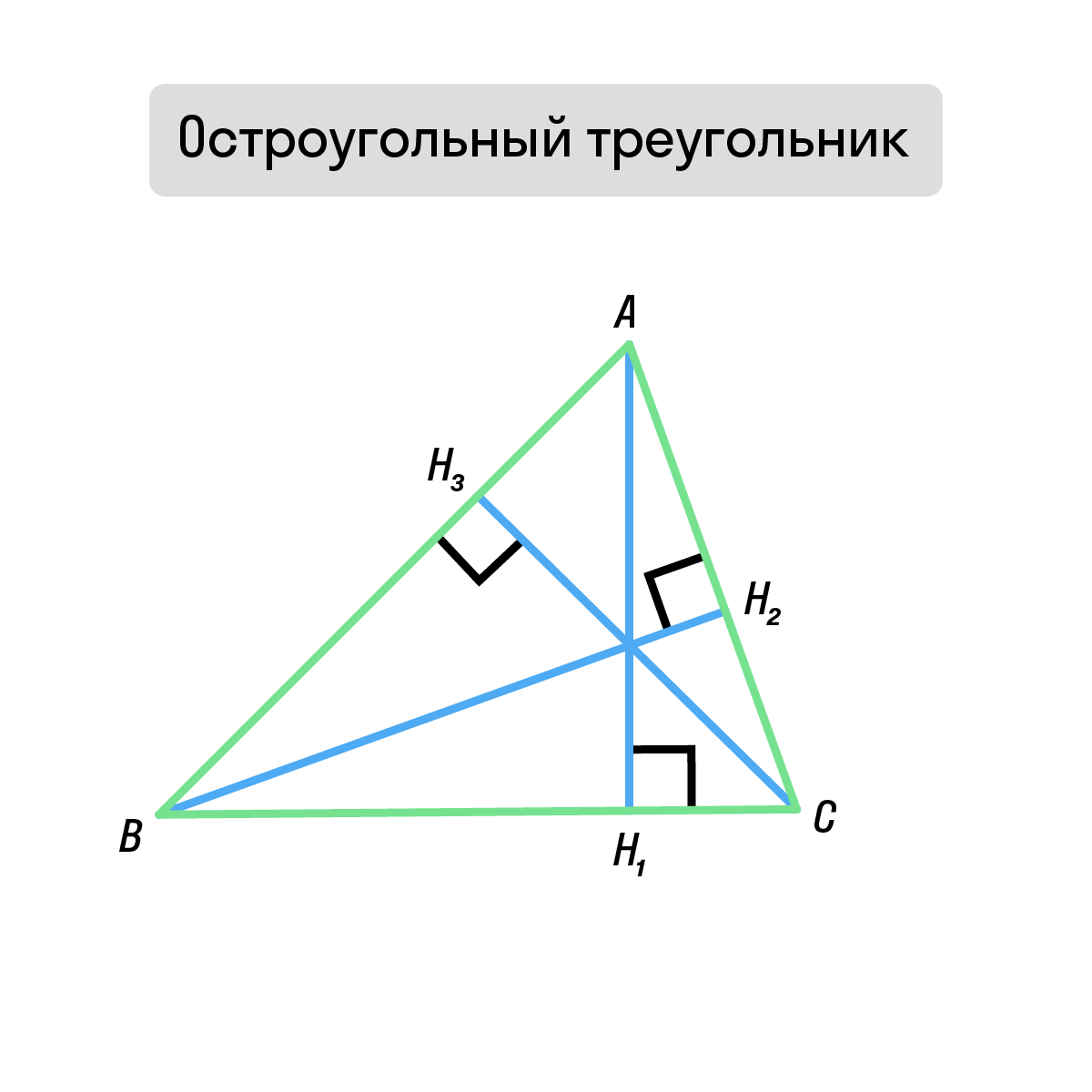
В зависимости от типа треугольника, высоты и точка их пересечения (ортоцентр) могут располагаться по-разному.
|
Остроугольный треугольник Высоты и точка их пересечения находятся внутри треугольника. |
|
|
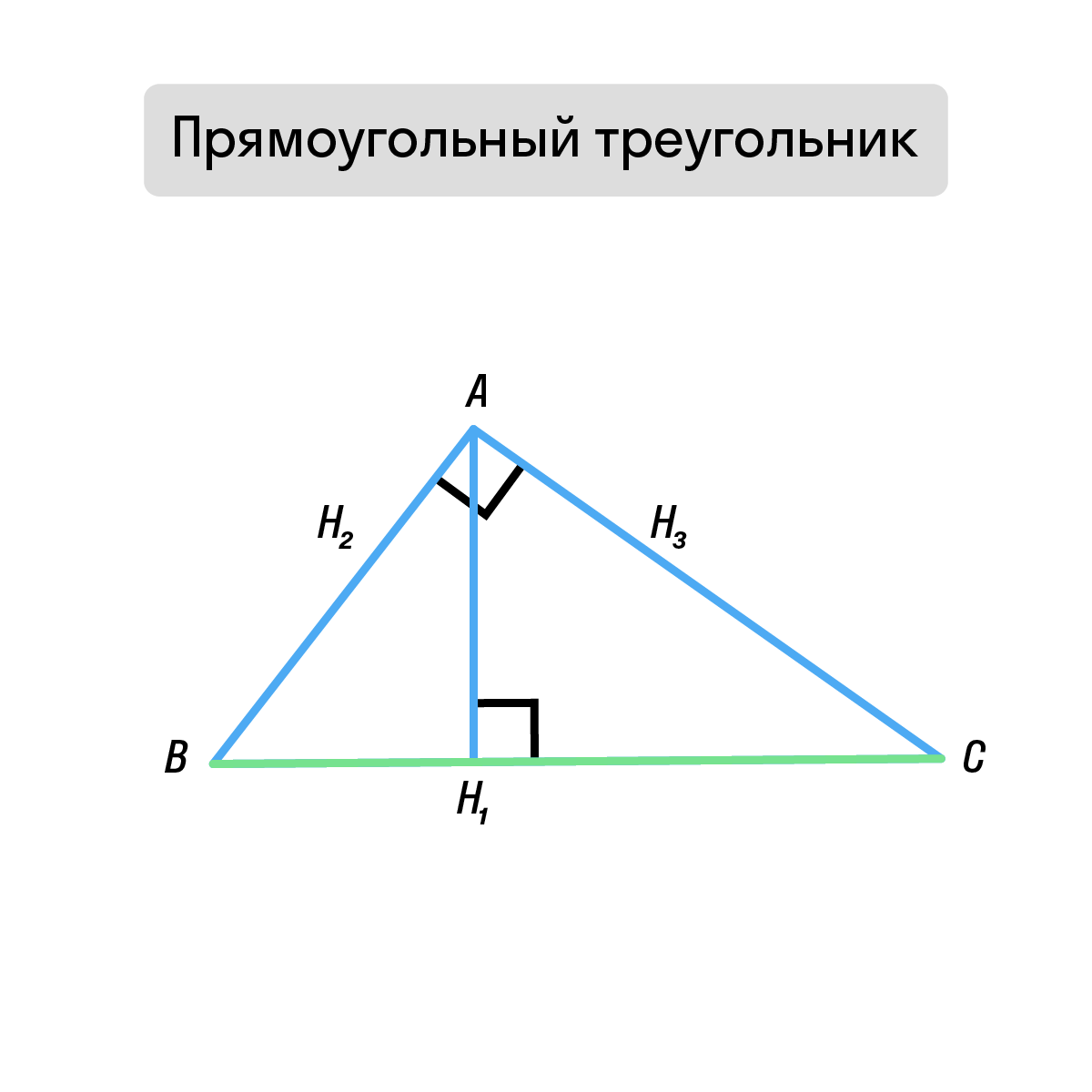
Прямоугольный треугольник Две высоты совпадают с катетами; точка пересечения находится в вершине прямого угла. |
|
|
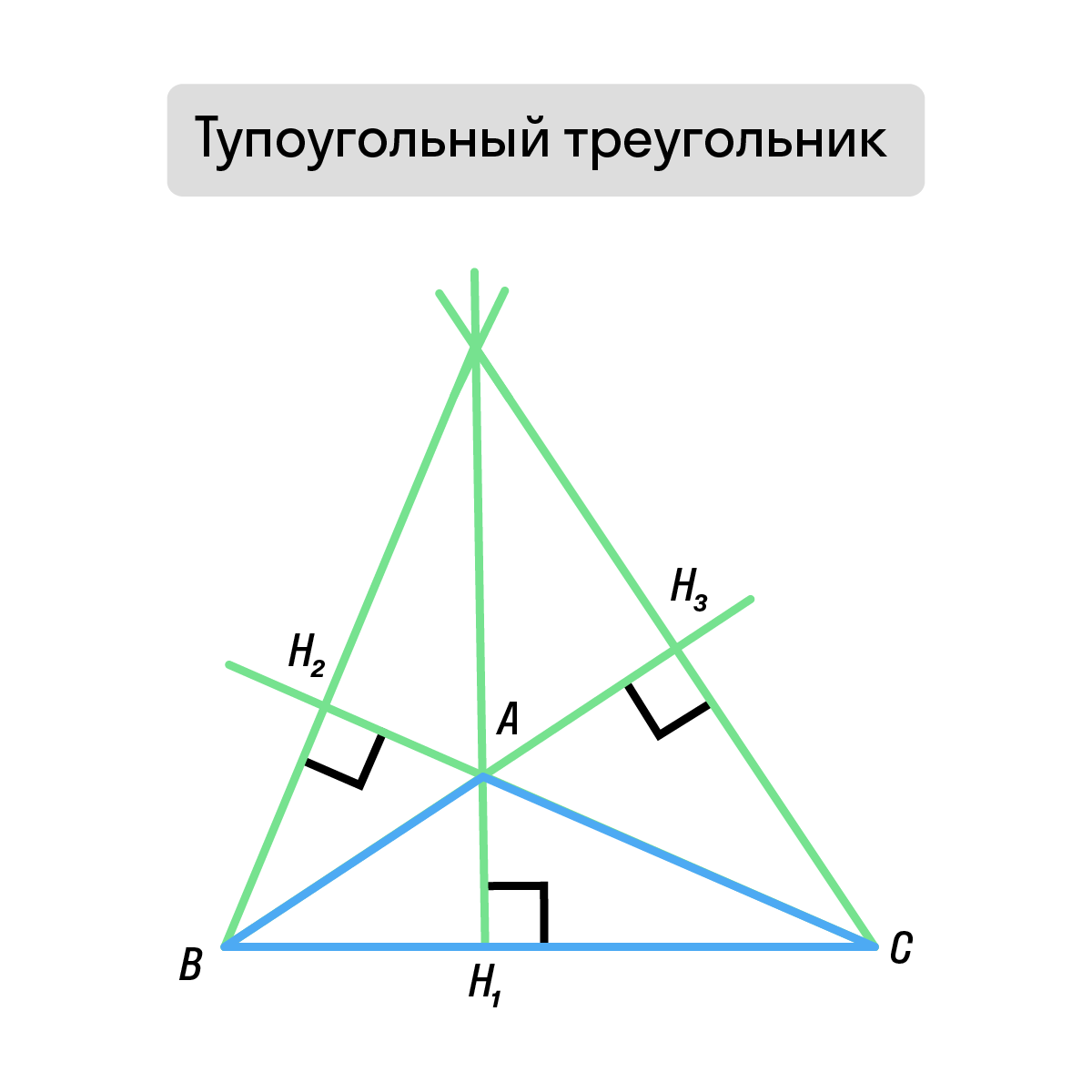
Тупоугольный треугольник Две высоты и точка пересечения лежат вне треугольника. |
|
В случае тупоугольного треугольника невозможно провести высоты из вершин острых углов так, чтобы они оставались внутри треугольника. Необходимо продлить боковые стороны и спроецировать высоты именно на продолжение (т. е. на прямую, которая содержит боковую сторону).
Любую высоту треугольника можно найти с помощью формул:
или
Интересные свойства высот в прямоугольном треугольнике:
-
Высоты, проведённые в прямоугольном треугольнике, связаны соотношением . Это соотношение ещё называют обратной теоремой Пифагора.
-
Высота, проведённая из вершины прямого угла, разделит гипотенузу на отрезки m и n. Тогда:
Длина
Одним из видов задач, которые вызывают затруднение у школьников, является нахождение длины биссектрисы угла треугольника. Первый вариант, в котором находится ее длина, содержит такие данные:
- величина пространства между лучами, из вершины которого выходит данный отрезок,
- длины сторон, которые образуют этот угол.
 Для решения поставленной задачи используется формула, смысл которой заключается в нахождении отношения увеличенного в 2 раза произведения значений сторон, составляющих угол, на косинус его половины к сумме сторон.
Для решения поставленной задачи используется формула, смысл которой заключается в нахождении отношения увеличенного в 2 раза произведения значений сторон, составляющих угол, на косинус его половины к сумме сторон.
Рассмотрим на определенном примере. Допустим, дана фигура АВС, в которой отрезок проведен из угла А и пересекает сторону ВС в точке К. Значение А обозначим Y. Исходя из этого, АК = (2*АВ*АС*cos(Y/2))/(АВ+АС).
Второй вариант задачи, в котором определяется длина биссектрисы треугольника, содержит такие данные:
известны значения всех сторон фигуры.
При решении задачи такого типа первоначально определяем полупериметр. Для этого необходимо сложить значения всех сторон и разделить пополам: р=(АВ+ВС+АС)/2. Далее применяем вычислительную формулу, с помощью которой определялась длина данного отрезка в предыдущей задаче. Необходимо только внести некоторые изменения в суть формулы в соответствии с новыми параметрами. Итак, необходимо найти отношение увеличенного в два раза корня второй степени из произведения длин сторон, которые прилегают к вершине, на полупериметр и на разность полупериметра и длины противолежащей ему стороны к сумме сторон, составляющих угол. То есть АК=(2٦АВ*АС*р*(р-ВС))/(АВ+АС).
Внимание! Чтобы легче освоить материал, можно обратиться к имеющимся в Интернете шуточным сказкам, повествующим о приключениях этой прямой
Прямоугольный треугольник и теорема Пифагора
article>СÑоÑÐ¾Ð½Ñ Ð² пÑÑмоÑголÑном ÑÑеÑголÑнике назÑваÑÑÑÑ Ð¿Ð¾-оÑобенномÑ. Так, ÑÑоÑона, лежаÑÐ°Ñ Ð½Ð°Ð¿ÑоÑив пÑÑмого Ñгла, назÑваеÑÑÑ Ð³Ð¸Ð¿Ð¾ÑенÑзой, она ÑÐ°Ð¼Ð°Ñ Ð±Ð¾Ð»ÑÑаÑ. Ðве дÑÑгие ÑÑоÑÐ¾Ð½Ñ â каÑеÑÑ. ÐÐµÐ¶Ð´Ñ Ð½Ð¸Ð¼Ð¸ ÑÑÑеÑÑвÑÐµÑ ÑооÑноÑение, именÑемое ÑеоÑемой ÐиÑагоÑа.
ÐажнÑе ÑвойÑÑва:
-
каÑеÑ, лежаÑий напÑоÑив Ñгла 30°, Ñавен половине гипоÑенÑзÑ;
-
в ÑавнобедÑенном пÑÑмоÑголÑном ÑÑеÑголÑнике оÑÑÑÑе ÑÐ³Ð»Ñ ÑÐ°Ð²Ð½Ñ 45°.
Все о прямоугольнике
Начнем со свойств прямоугольника.
- Все углы прямые.
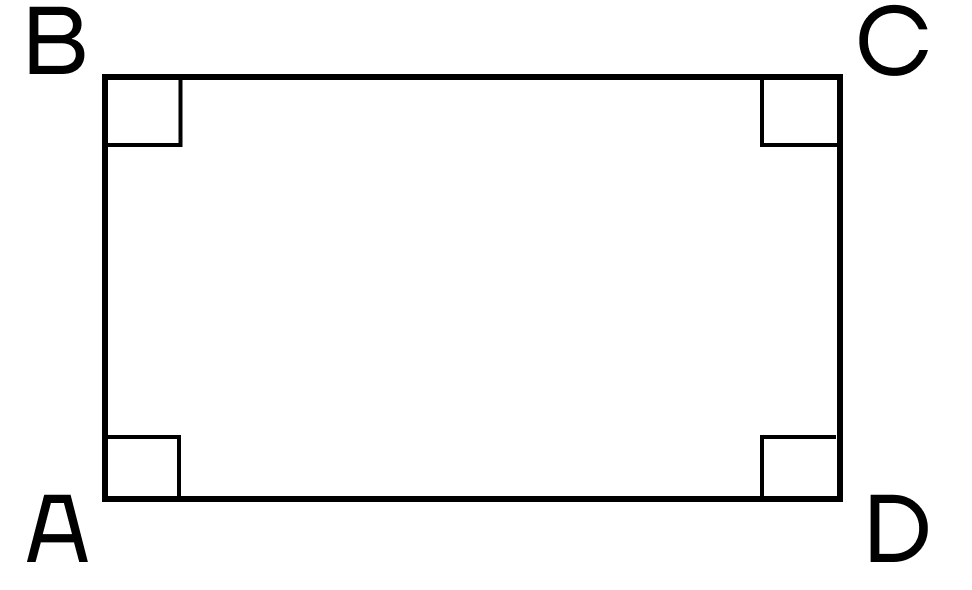
- Диагонали равны.
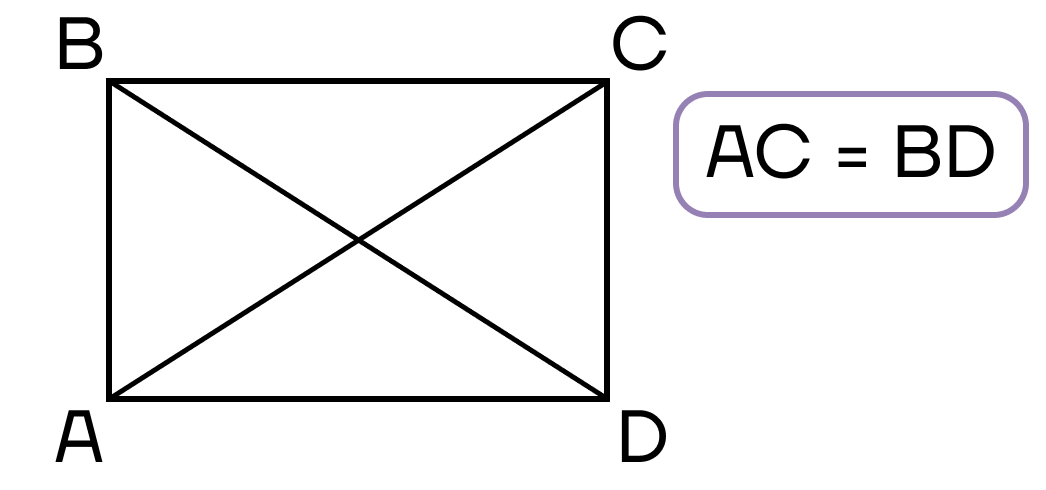
- Стороны прямоугольника одновременно являются и его высотами.
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали. Это теорема Пифагора.
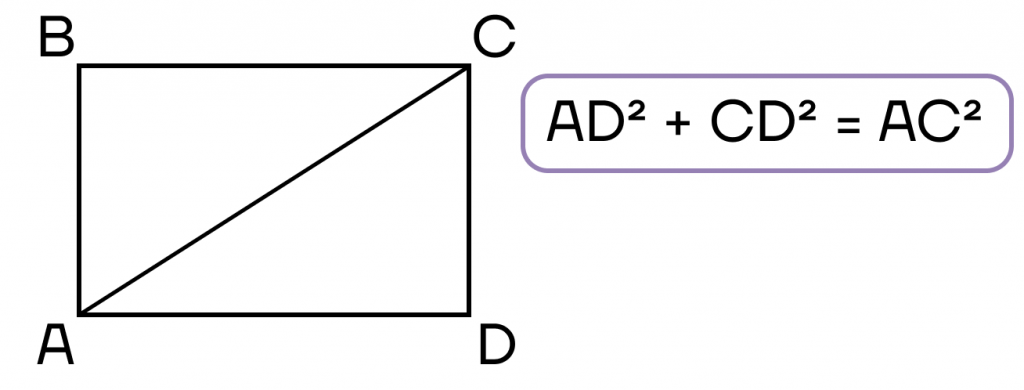
Со свойствами разобрались, теперь рассмотрим признаки.
- Параллелограмм, имеющий хотя бы один прямой угол, — прямоугольник.
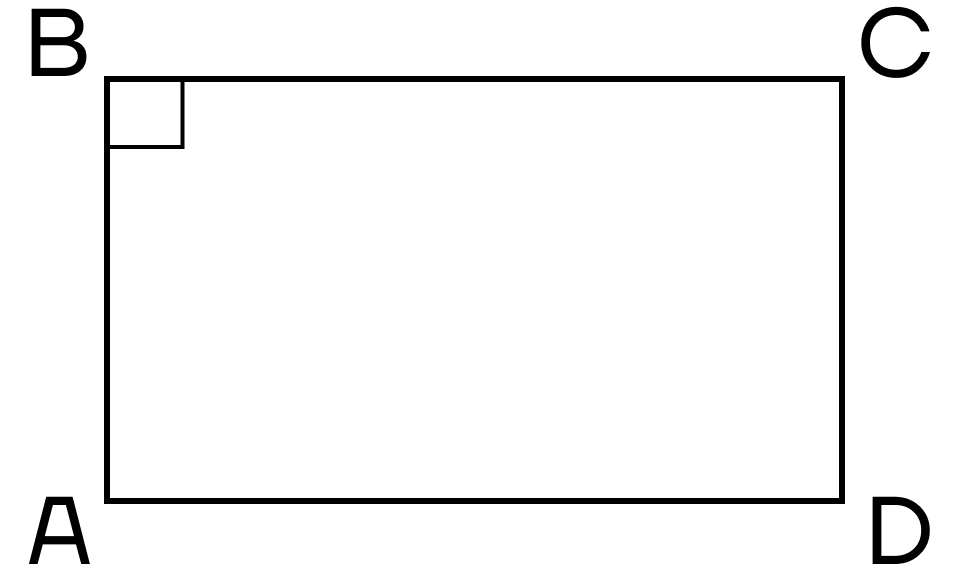
- Параллелограмм, все углы которого равны, — прямоугольник.
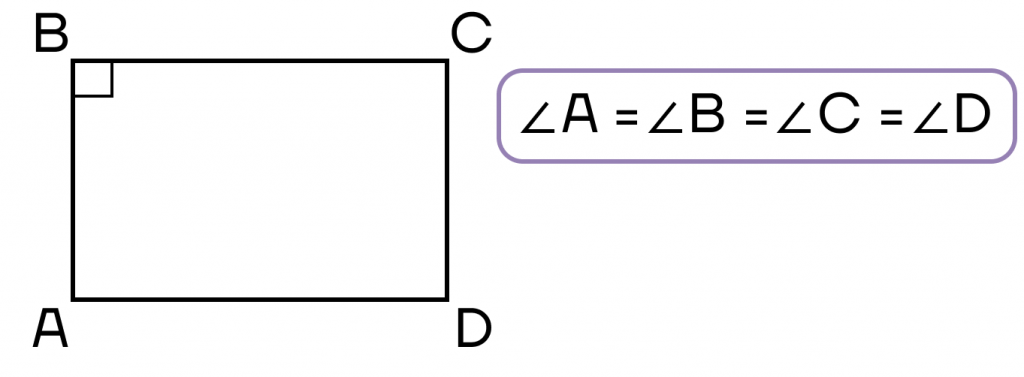
- Параллелограмм, диагонали которого равны, — прямоугольник.
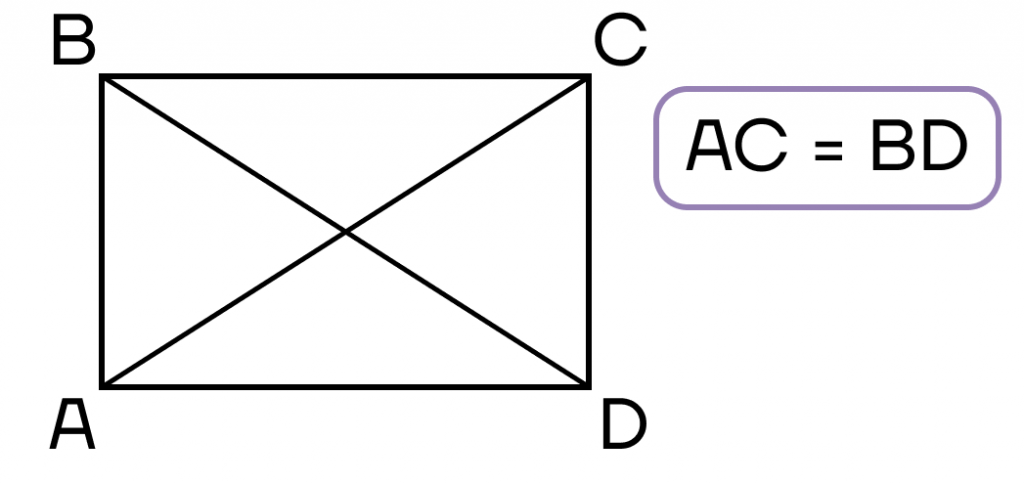
- Четырехугольник, у которого три прямых угла, — прямоугольник.
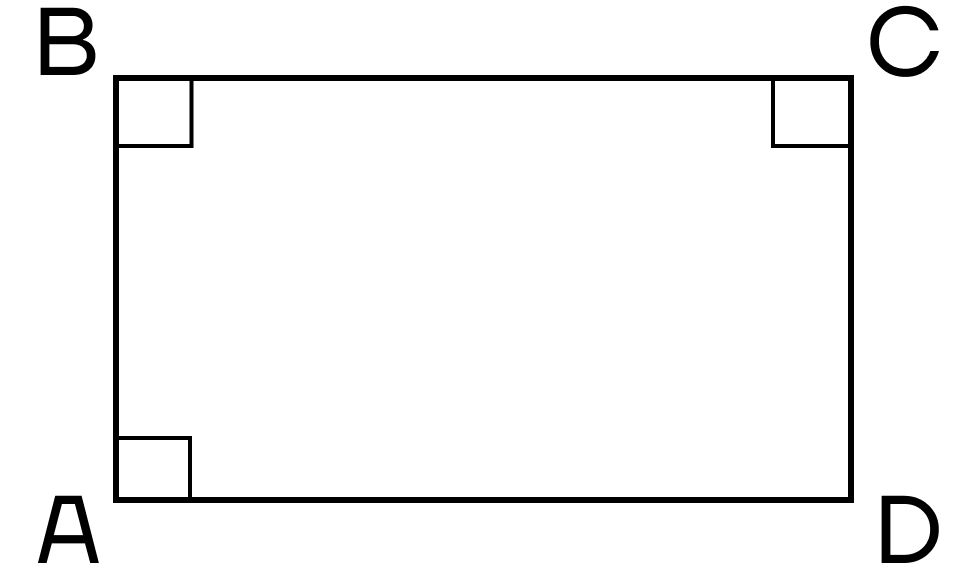
Так, а что там у нас с биссектрисами в прямоугольнике?
А с биссектрисами все достаточно легко. Биссектриса делит угол прямоугольника на два угла по 45° и пересекает одну из сторон прямоугольника.
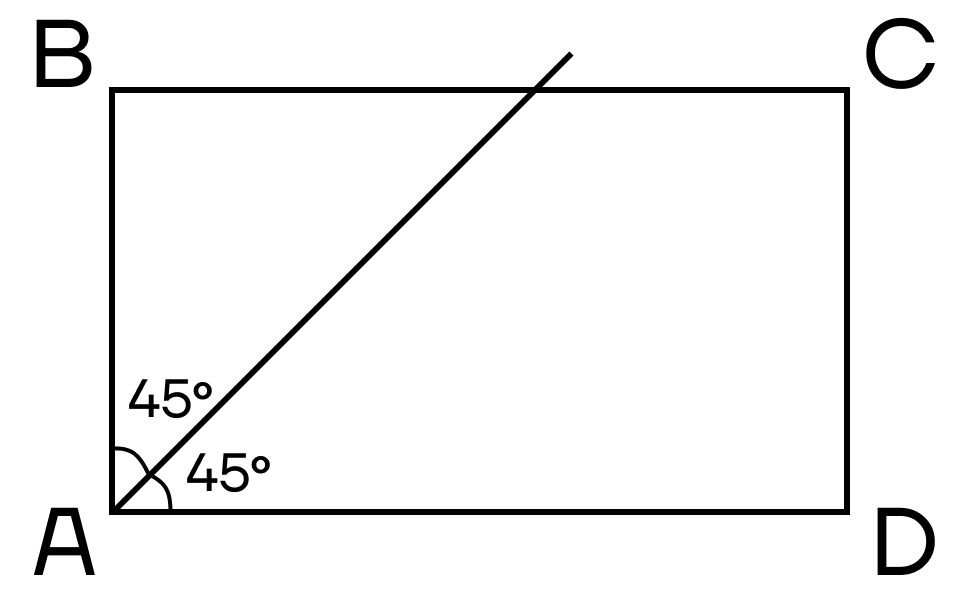
Теперь рассмотрим два способа нахождения площади прямоугольника.
- Площадь прямоугольника равна произведению двух соседних сторон.
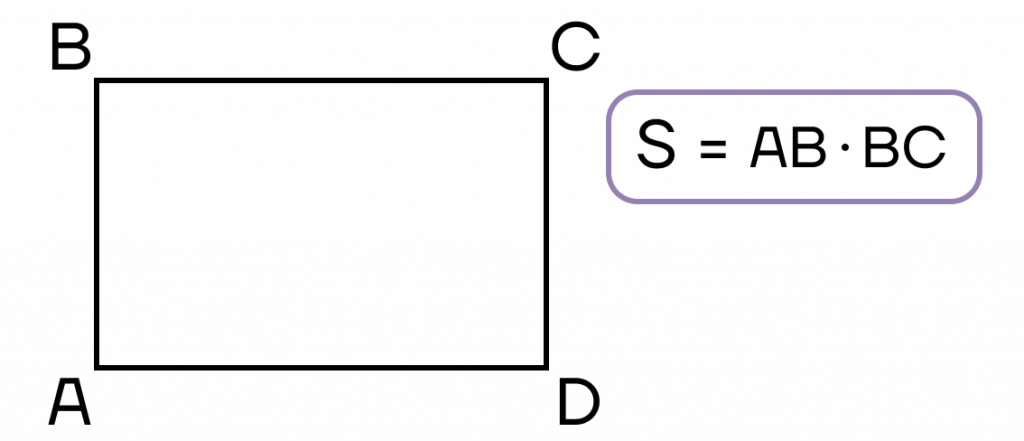
- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
| Во что можно поиграть на уроках и вспомнить геометрию?1. Итак, запоминайте алгоритм.Бросаете два кубика.2. Делаете прямоугольник с размером сторон, которые сгенерировал кубик.3. Новый прямоугольник обязательно должен быть соединен с любым другим вашим прямоугольником.4. Если это ваш первый прямоугольник, то поместите его в любой угол, а соперник должен поместить свой в противоположный.5. Если у вас не получается создать прямоугольник с получившимися сторонами, то вы пропускаете ход.6. Игра заканчивается, когда вся территория занята. Побеждает тот, у кого наибольшая территория. |
Давайте закрепим материал на примере.
Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.Задание. Площадь прямоугольника равна 20. Найдите его большую сторону, если она на 8 больше меньшей стороны.

Решение. Как мы уже знаем, площадь прямоугольника равна произведению длины на ширину. Примем одну сторону прямоугольника за x, тогда вторая равна x + 8.Тогда:\(S=x*(x+8)=20\)\(x^2+8x-20=0\)Решим квадратное уравнение:\(D=8^2-4*1*(-20)=64+80=144\)Корни уравнения:\(x_{1,2}=\frac{-8\pm 12}{2}\)Первый корень:\(x_1=\frac{-8+12}{2}=\frac{4}{2}=2\)Второй корень:\(x_2=\frac{-8-12}{2}=-\frac{20}{2}=-10\)Сторона не может иметь отрицательную длину, поэтому верный корень — первый. Это наименьший корень, а значит больший:\(x=2+8=10\)Ответ: 10

На этом заканчивается наша статья, но не тема четырехугольников. В следующей статье мы продолжим изучать их и узнаем про ромб и квадрат. Читайте здесь: «Параллелограмм. Часть 2».
Свойства биссектрисы треугольника
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.
Благодаря этому утверждению, легко доказывается следующее правило:
Площадь описанного многоугольника равна:
S = p∗r
где p – полупериметр, а r – радиус вписанной окружности.
Это позволяет находить решение не только планиметрических, но и стереометрических задач.
Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.
Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;
4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.
В этом случае основание параллельно внешней биссектрисе.
Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;
5
Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;. 6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
У правильного треугольника все внешние биссектрисы параллельны сторонам;
6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
7. Выделяют несколько особенностей, среди которых есть следующая теорема:
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.
https://youtube.com/watch?v=FLMq8v1ysgU
Основное свойство биссектрисы угла
На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:
В переводе с математического на русский это означает сразу два факта:
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $H\in l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.
Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:
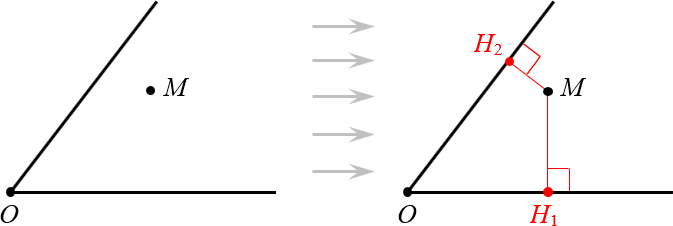
Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.
Как и обещал, разобьём доказательство на две части:
1. Расстояния от точки на биссектрисе до сторон угла одинаковы
Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.
2. Если расстояния равны, то точка лежит на биссектрисе
Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:
Докажем, что луч $OM$ — биссектриса, т.е. $\angle MO{{H}_{1}}=\angle MO{{H}_{2}}$.
Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)
Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.
Три биссектрисы в треугольнике пересекаются в одной точке
Из свойства биссектрисы быть геометрическим местом точек, равноудаленных от сторон угла, вытекает следующее утверждение:
Как именно вытекает? А вот смотри: две-то биссектрисы точно пересекутся, правда?
А третья биссектриса могла бы пройти так:
Но на самом деле-то всё гораздо лучше!
Давай рассмотрим точку пересечения двух биссектрис. Назовём её .
Что мы тут оба раза применяли? Да пункт 1
, конечно же! Если точка лежит на биссектрисе, то она одинаково удалена от сторон угла.
Вот и получилось и.
Но посмотри внимательно на эти два равенства! Ведь из них следует, что и, значит, .
А вот теперь в дело пойдёт пункт 2
: если расстояния до сторон угла равны, то точка лежит на биссектрисе…какого же угла? Ещё раз смотри на картинку:
и — расстояния до сторон угла, и они равны, значит, точка лежит на биссектрисе угла. Третья биссектриса прошла через ту же точку! Все три биссектрисы пересеклись в одной точке! И, как дополнительный подарок —
Радиусы вписанной
окружности.
(Для верности посмотри ещё тему ).
Ну вот, теперь ты никогда не забудешь:
Точка пересечения биссектрис треугольника — центр вписанной в неё окружности.
Переходим к следующему свойству… Ух и много же свойств у биссектрисы, правда? И это здорово, потому что, чем больше свойств, тем больше инструментов для решения задач про биссектрису.
Биссектрисы треугольника
Круги, вписанные и не вписанные в треугольник — В треугольнике:
- Внутренние биссектрисы совпадают, их точка пересечения — это центр окружности, вписанной в треугольник. Этот круг касается трех сторон треугольника;
- Две внешние биссектрисы пересекаются с оставшейся внутренней биссектрисой. Таким образом, мы получаем центры трех окружностей, вписанных в треугольник;
- Круг, проходящий через основания внутренней биссектрисы, также проходит через точку Фейербаха .
Биссектриса внутри треугольника, исходящая из вершины ( например, A ), имеет длину 2 bc cos (A / 2) / (b + c).
Угол, образованный двумя внутренними биссектрисами BI и CI ( например ), равен (π + A) / 2
Угол, образованный внешними биссектрисами BI ‘и CI’ ( например ), равен (π-A) / 2
Особенность: в треугольнике ABC внутренняя биссектриса вершины (C) пересекает серединный перпендикуляр противоположного сегмента (AB) в точке S на описанной окружности.
Круг с центром S, проходящий через A (и B), также проходит через центр круга, вписанного в ABC.
Доказательство —
Для первой точки теоремы, точка пересечения двух внутренних биссектрис равноудалена от трех сторон треугольника. Таким образом, он также находится на третьей внутренней биссектрисе. Окружность с центром в точке пересечения и касательной к одной стороне будет касаться двух других (примените следствие теоремы о биссектрисе (бис)).
Теорема — В треугольнике ABC с I по , линия (CI) , является внутренней биссектрисой из C тогда и только тогда .
ПРОТИВВПРОТИВBзнак равнояВяB{\ displaystyle {\ frac {CA} {CB}} = {\ frac {IA} {IB}}}
Доказательство теоремы Фалеса приведено на странице о . Двустороннее вычисление площадей треугольников CAI и CBI дает еще одно базовое доказательство.
Затем мы можем вычислить длины отрезков, которые внутренняя биссектриса из C разрезает на противоположной стороне:
Мы получаем: и . Или снова с классическими обозначениями: и яВПРОТИВВзнак равнояBПРОТИВBзнак равнояВ+яBПРОТИВВ+ПРОТИВBзнак равноВBПРОТИВВ+ПРОТИВB{\ displaystyle {\ frac {IA} {CA}} = {\ frac {IB} {CB}} = {\ frac {IA + IB} {CA + CB}} = {\ frac {AB} {CA + CB }}}яВзнак равноВB⋅ПРОТИВВПРОТИВВ+ПРОТИВB{\ Displaystyle IA = {\ гидроразрыва {AB \ cdot CA} {CA + CB}}}яBзнак равноВB⋅ПРОТИВBПРОТИВВ+ПРОТИВB{\ Displaystyle IB = {\ гидроразрыва {AB \ cdot CB} {CA + CB}}}Иксзнак равнопротивбб+в{\ displaystyle x = {\ frac {cb} {b + a}}}yзнак равнопротиввб+в{\ displaystyle y = {\ frac {ca} {b + a}}}
Приложения:
- Предыдущая характеризация биссектрисы широко используется при изучении проблемы Аполлония : геометрическое место M такое, что MA / MB = k.
- С помощью этой характеристики биссектрисы мы легко находим биссектрису угла MFN, где M и N — две точки на (в более общем смысле, правильная коника) с фокусом F и директрисой D, а также построение касательной в точке коническая
Биссектриса — это.
Биссектриса угла — это луч, который начинается из вершины треугольника и делит его ровно пополам.

Кроме того, биссектриса угла — это длина отрезка (что это такое?), который начинается в вершине треугольника и заканчивается на противоположной стороне вершины.
Существует также понятие «биссектриса угла», которая является радиусом и делит угол (любой угол, не обязательно треугольник) пополам таким же образом:
Термин bisectrix происходит из латинского языка. И название очень характерное. Оно состоит из двух слов — «bi» означает «двойной, пара», а «sectio» можно буквально перевести как «разрезать, разделять».
Получается, что слово BISSECTRISA означает «разрезать пополам», что и отражено в только что приведенном определении термина.
А теперь проект по закреплению материала. Посмотрите на эти рисунки и скажите, на каком из них изображена дихотомия. Подумайте об этом? Правильно, второй.
На первом рисунке луч, выходящий из угла AOB, явно не делит его пополам. Во втором случае эта связь углов более очевидна, и поэтому можно предположить, что радиус OD — БИССЕКТРИСА. Хотя, конечно, трудно утверждать это на сто процентов.
Для более точного определения используются специальные инструменты. Например, транспортир. Это инструмент в виде полусферы, изготовленный из металла или пластика. Это выглядит следующим образом:

Однако существуют и такие варианты:
Я уверен, что в школе у каждого был такой. И он очень прост в использовании. Просто совместите основание транспортира (прямоугольной линейки) точно с основанием треугольника, а затем отметьте на полусфере значение, соответствующее величине угла.
И точно такая же система может быть применена в обратном направлении: С помощью транспортира начертите угол нужного размера. Обычно он составляет от 0 до 180 градусов. Но на втором рисунке у нас есть транспортир, который помогает нам чертить градусы от 0 до 360.