Определение и значения
Сумма координат — это математическое понятие, которое применяется в геометрии и алгебре. Оно описывает результат сложения всех числовых значений координат точек в заданной системе координат.
Значение суммы координат может быть положительным, отрицательным или равным нулю в зависимости от точек, для которых производится вычисление. В двумерной системе координат сумма будет представлена двумя числами: первое число — сумма абсцисс (координат по оси X), второе — сумма ординат (координат по оси Y).
В трехмерной системе координат сумма будет включать в себя три числа: сумму абсцисс (координат по оси X), сумму ординат (координат по оси Y) и сумму аппликат (координат по оси Z).
Значение суммы координат может быть использовано для различных вычислений и анализа данных. Например, в геометрии сумма координат может быть использована для нахождения центра масс или центра тяжести системы точек. В алгебре сумма координат может быть использована для решения линейных уравнений или систем уравнений.
Примеры вычисления суммы координат:
- В двумерной системе координат имеется две точки: A(3, -2) и B(-1, 4). Чтобы найти сумму координат, нужно сложить соответствующие значения: XA + XB = 3 + (-1) = 2, YA + YB = (-2) + 4 = 2. Таким образом, сумма координат точек A и B равна (2, 2).
- В трехмерной системе координат имеется три точки: C(1, 2, 3), D(-2, 0, 5) и E(4, -1, -2). Для нахождения суммы координат нужно сложить значения по каждой оси: XC + XD + XE = 1 + (-2) + 4 = 3, YC + YD + YE = 2 + 0 + (-1) = 1, ZC + ZD + ZE = 3 + 5 + (-2) = 6. Таким образом, сумма координат точек C, D и E равна (3, 1, 6).
Что такое координатные числа?
Координатные числа — это способ представления точек на плоскости или в пространстве с помощью числовых значений, которые называются координатами.
На плоскости используется двумерная система координат, которая состоит из двух осей — горизонтальной (ось абсцисс) и вертикальной (ось ординат). Каждая точка на плоскости имеет свои координаты, которые обозначаются парой чисел (x, y), где x — значение на оси абсцисс, а y — значение на оси ординат.
Например, точка A с координатами (2, 3) находится на 2 единицы правее начала координат и на 3 единицы выше него.
В трехмерном пространстве используется трехмерная система координат, которая добавляет еще одну ось — ось глубины (ось аппликат). Таким образом, каждая точка в пространстве имеет тройные координаты (x, y, z), где x — значение на оси абсцисс, y — значение на оси ординат, а z — значение на оси аппликат.
Координатные числа используются для описания положения и перемещения объектов в графике, конструкциях, физике, геометрии и многих других областях науки и техники.
Нахождение угла
Например, необходимо найти угол между плоскостями. Координатным методом решить поставленную задачу несложно. С точки зрения геометрии, это угол между двумя параллелями. Отметив на поверхности начало координат, через него можно провести перпендикуляры обеим плоскостям. Образованный угол и будет искомым. Поэтому для решения задачи необходимо:
- записать уравнения плоскостей;
- составить векторы нормали;
- вычислить значение косинуса угла между поверхностями.

Для составления уравнений следует найти положение трёх точек, лежащих в плоскости, но не на одной нормали. Затем каждое из них подставить в уравнение и получить систему. Решается последняя любым доступным методом, например, нахождением определителя матрицы или графическим смешанным методом. В итоге находят корни системы A, B, C и составляют вектор нормали. При этом полученные координаты не должны быть коллинеарными, то есть не лежать на одной прямой или быть параллельными.
Пусть имеется единичный куб, в котором нужно найти угол, образованный A1, B1, C1 и C1, D, A1. Вначале определяют координаты первой плоскости и подставляют их в уравнение: Ax+By+Cz+1 = 0. Тут следует отметить: свободный член добавляется из-за того, что поверхности не проходят через середину координат. Точки определяются значениями: A1 (1, 0, 1), B (0,0,1), D (1,1,0). После подстановки система уравнений примет вид:
{A + 0 +C + 1 = 0;
{0 + 0 + C + 1 = 0;
{A + B + 0 + 1 = 0.

Из второго равенства можно определить C. Подставив найденное C в первое равенство, можно выразить A, а после найти B. Таким образом, решением системы будет A = 0, B = -1, C = -1. Вектор нормали, соответственно, будет: N1 (0; -1; -1).
Чтобы составить уравнение второй плоскости, нужно найти координаты лишь С1. Исходя из условия, они будут равны С1 (0; 1; 1), а A и D уже известны. Подставляя данные в уравнение Ax+By+Cz+1 = 0, опять составляют систему и находят её коэффициенты. После решения второй матрицы, например, методом разложения, можно записать координаты второго вектора: N2 (-½; ½; -½).
Теперь, когда известны N1 и N2, нужно найти косинус между ними, являющийся углом двух искомых плоскостей. Используя формулу для вычисления угла векторов, можно получить следующее: cosα = |½ + ½| / (2½ * ¾½) = 1 / (6½/2) = 2/6½ = 6½ / 3. Соответственно, угол равен: α = arccos = 6½ / 3.
Так где же стоит использовать беззнаковые числа?
В C++ всё же есть несколько случаев, когда можно (или необходимо) использовать беззнаковые числа.
Во-первых, числа без знака предпочтительнее при работе с битами (рассматривается в главе O (это заглавная буква «о», а не «0»).
Во-вторых, использование беззнаковых чисел всё еще неизбежно в некоторых случаях, в основном тех, которые связаны с индексацией массивов. Подробнее об этом мы поговорим в уроках по массивам и индексированию массивов.
Также обратите внимание, что, если вы разрабатываете для встраиваемой системы (например, Arduino) или какого-либо другой системы с ограничениями процессора/памяти, использование чисел без знака более распространено и приемлемо (а в некоторых случаях неизбежно) по соображениям производительности
Аффинная и декартова системы координат
Если рассматривать все системы отсчета с кинематической точки зрения, они похожи. Кинематика не указывает на преимущества одной системы отсчета перед другой. Для удобства решения была выбрана наиболее приемлемая система. Чтобы описать пространство, в котором движется материальная точка, система отсчета связана с системой пространственных координат.
Определения
Система пространственных координат — это набор определений, которые могут реализовать метод координат, то есть определение положения точки или тела с помощью чисел или символов.
Числа, которые могут обозначать положение выбранной точки в трехмерном пространстве, называются координатами этой точки.
Аффинная система координат
Аффинная система координат образована тремя линейно независимыми векторами (осями координат), исходящими из точки, то есть из начала координат.
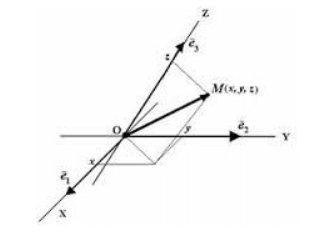 Рис. 1. Положение точки в аффинной системе координат
Рис. 1. Положение точки в аффинной системе координат
Этот случай показывает, что положение материальной точки MM в пространстве определяется радиус-вектором проведенным через начало системы координат в данную точку, движение можно представить как сумму векторов независимых перемещений вдоль три пространственные оси выбранной системы координат
Декартова система координат
Декартовы координаты позволяют определять положение точки на плоскости или трехмерном пространстве. Декартовы координаты (также называемые прямоугольными координатами) точки — это пара чисел (в двух измерениях) или тройка чисел (в трех измерениях), которые определяют расстояния со знаком от оси координат.
Чаще всего используется декартова система координат, состоящая из взаимно перпендикулярных осей x, y, z Данная система применима для описания прямолинейного движения и движения по разомкнутым или нециклическим кривым. Это визуальная геометрическая интерпретация с простыми вычислениями.
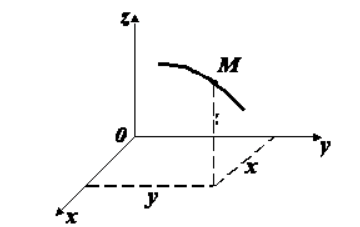 Рис. 2 Положение точки в декартовой системе координат
Рис. 2 Положение точки в декартовой системе координат
Упражнения
Упражнение 1: Практика объявления переменных
Вам предстоит создать программу, которая будет сохранять информацию о студенте. Используйте разные типы данных для различных характеристик:
Copy
Ваша задача: Добавьте дополнительные характеристики студента и объявите переменные для их хранения. Используйте разные типы данных в соответствии с характером информации (например, дата рождения, адрес).
Решение
Copy
Упражнение 2: Приведение типов и операции с переменными
Представьте, что у вас есть следующая информация:
Copy
Вам нужно рассчитать общую стоимость покупки и вывести результат на экран.
Ваша задача:
-
Создайте переменную и рассчитайте общую стоимость покупки, умножив цену за единицу товара на количество товаров.
-
Выведите результат на экран в виде строки, например: «Общая стоимость покупки: $59.97».
-
После этого измените тип данных переменной на целочисленный () и повторите расчет. Выведите новый результат на экран.
-
Объясните, почему произошли изменения в результатах при изменении типа данных переменной .
Решение
Copy
Определение координаты:
Координата — это числовое значение, которое определяет расположение точки, объекта или местоположения в пространстве или на плоскости. Координатной системой называется система чисел, используемая для определения координаты.
В математике и физике координаты обычно используются для описания положения объекта относительно определенной точки или начала отсчета. Один из наиболее распространенных видов координатной системы — декартова система координат. Она состоит из осей, пересекающихся в точке, называемой началом координат. Координаты точки в этой системе представляют собой пару чисел, которая показывает расстояние по каждой оси от начала координат.
В географии используется географическая система координат для определения местоположения на поверхности Земли. Она использует широту и долготу для указания положения точки на глобусе. Широта определяет расстояние от точки до экватора, а долгота — расстояние от точки до оси, проходящей через Гринвич.
Координаты также широко используются в информатике и программировании для определения расположения объектов на экране компьютера или в трехмерном пространстве. В компьютерной графике координаты задают положение пикселя на экране, а в трехмерной графике используются трехмерные координаты для определения положения объекта в пространстве.
В общем случае определение координаты позволяет установить положение объекта в пространстве и может быть полезным инструментом при анализе данных или визуализации информации.
История и развитие понятия «координата»
Координата – это величина, позволяющая определить положение точки или объекта в пространстве или на плоскости. Термин «координата» происходит от латинского слова «co-ordinare», что означает «согласовывать». Понятие координат развивалось в течение многих веков и имело свои истоки в различных культурах и областях знания.
В Древнем Египте и Месопотамии (более 5000 лет назад) ученые использовали систему пространственных координат для определения местоположения звезд и планет. Они использовали сферические координаты, чтобы определить высоту и азимут звезд. Эта система имела основу в географических представлениях, и была использована для навигации и астрономии.
В Древней Греции (4-5 век до н.э.) философы и ученые также разработали собственную систему координат – географические координаты. Эта система, основанная на широте и долготе, использовалась для определения местонахождения на поверхности Земли.
Однако, с развитием математики в средние века и в период Возрождения, понятие координат претерпело существенные изменения. В 17 веке, французский математик Рене Декарт разработал декартову систему координат, которая стала основой для аналитической геометрии и алгебры. Он предложил использовать число и оси для представления геометрических фигур и решения математических задач.
С развитием науки и технологий понятие координат стало широко применяться во множестве областей, включая математику, физику, инженерию, географию, компьютерную графику и многие другие. Сегодня координаты являются важным инструментом для измерения и описания положения объектов в пространстве.
В заключение, понятие координат имеет древние истоки и развивалось на протяжении многих лет. От пространственных координат Древнего Египта и Месопотамии до декартовой системы координат, оно играло и продолжает играть важную роль в научных и практических исследованиях, позволяя точно определить и согласовывать положение объектов.
Компьютерная графика и стандарт OpenGL стр.97
Значения координат хО, уО, xOffset и yOffset, а также текущее растровое положение сохраняются в виде чисел с плавающей запятой. Конечно, битовое отображение применяется в пикселях с целочисленными координатами. Однако координаты в виде чисел с плавающей запятой позволяют размещать битовое отображение через произвольные интервалы, что очень полезно в некоторых приложениях, таких как формирование строк символов с помощью битовых узоров.
Чтобы задать координаты текущего растрового положения, применяется следующая процедура:
glRasterPos* ( )

Рис. 3.61. Битовый узор, представленный в виде массива из 10 строк и 9 столбцов, записывается с помощью 8-битовых блоков из 10 строк с 16 значениями в каждой строке Параметры и индексы аналогичны тем, которые используются в функции glVertex. Таким образом, текущее растровое положение задается во внешних координатах, а затем преобразуется в экранные координаты с помощью изменения точки наблюдения. В использованных двухмерных примерах координаты текущего растрового положения можно задавать непосредственно в целочисленных экранных координатах. По умолчанию значение текущего растрового положения совпадает с началом отсчета (0, 0, 0) внешней системы координат.
Цветом битового отображения является текущий цвет в момент вызова команды glRasterPos. Любые последующие изменения цвета не влияют на битовый массив.
Каждая строка прямоугольного битового массива записывается в виде чисел, размер которых кратен 8 бит, где бинарные данные организованы в виде 8-битовых символов без знака. Однако фигуру также можно описать с помощью сетки любого другого удобного размера. В качестве примера на рис. 3.61 показан битовый узор, заданный с помощью сетки из 10 строк и 9 столбцов, где бинарные данные задаются с помощью 16 бит в каждой строке. Когда этот узор накладывается на пиксели в буфере кадра, все значения битов за пределами девятого столбца игнорируются.
Чтобы наложить битовый узор, изображенный на рис. 3.61, на определенный участок буфера кадра, воспользуемся следующим кодом.
GLubyte bitShape =
0x1с, 0x00, 0x1с, 0x00, Oxlc, 0x00, 0x1c, 0x00, 0x1c, 0x00,
Oxff, 0x80, 0x7f, 0x00, 0x3e, 0x00, Oxlc, 0x00, 0x08, 0x00;
glPixelStorei (GL_UNPACK_ALIGNMENT, 1);
/* Устанавливается режим хранения пикселей. */
glRasterPos2i (30, 40);
glBitmap (9, 10, 0.0, 0.0, 20.0, 15.0, bitShape); Значения массива bitShape задаются построчно, начиная с нижнего края прямоугольной сетки узора. Затем устанавливается режим хранения битового отображения с помощью стандартной процедуры OpenGL glPixelStorei. Значение 1 в этой функции указывает на то, что заданные значения следует располагать по границам байтов. С помощью функции glRasterPos устанавливается текущее растровое положение с координатами (30, 40). Наконец, функция glBitmap указывает, что битовый узор задается в виде массива bitShape, и что этот массив состоит из 9 столбцов и 10 строк. Координаты точки отсчета этого узора — (0.0, 0.0), т.е. она находится в левом нижнем углу сетки. На данном рисунке иллюстрируется смещение координат на величину (20.0, 15.0), хотя в данном примере оно никак не используется.
⇐ вернуться назад | | далее ⇒
Приведение типов
Приведение типов представляет собой процесс изменения типа переменной от одного к другому. В C# существует два вида приведения типов: явное и неявное.
Явное приведение типов осуществляется с использованием оператора приведения. Например:
Copy
Неявное приведение типов автоматически выполняется компилятором. Например:
Copy
Приведение типов является важным инструментом при работе с различными данными, и его использование требуется в определенных сценариях программирования.
С этими инструментами – объявлением переменных и приведением типов – вы можете более гибко управлять данными в вашей программе, что является ключевым моментом в разработке на C#. Они позволяют создавать более сложные и эффективные программы, а также обеспечивают точное управление данными в различных сценариях.
Значение целочисленных координат при измерениях
Целочисленные координаты играют важную роль при измерениях в различных областях, таких как геометрия, физика, компьютерная графика и многих других. В данном контексте целочисленные координаты обозначаются как пара чисел: X и Y.
Координата X обозначает горизонтальное расположение объекта на плоскости, а координата Y обозначает вертикальное расположение. Значение координат задает точку, которую можно считать началом координатной системы.
| Координата | Значение | Применение |
|---|---|---|
| X | Целое число отрицательное или положительное | Определение положения объекта относительно других объектов |
| Y | Целое число отрицательное или положительное | Определение вертикального положения объекта |
Значение целочисленных координат позволяет точно определить положение объекта в пространстве и использовать его в различных математических вычислениях, визуализации данных и других операциях. Например, в компьютерной графике, координаты используются для отображения точек на экране и определения масштабирования, вращения или перемещения объектов.
Таким образом, значение целочисленных координат при измерениях является важным элементом для точного позиционирования и визуализации объектов в различных областях науки и техники.
Примеры вычисления суммы координат
Рассмотрим несколько примеров вычисления суммы координат для разных типов координат.
Пример 1: Сумма координат точек
Допустим, у нас есть две точки на плоскости с координатами (2, 3) и (-1, 5).
Для вычисления суммы координат, сложим соответствующие координаты:
(2 + (-1), 3 + 5) = (1, ![]()
Пример 2: Сумма координат векторов
Предположим, у нас есть два вектора со следующими координатами: A(2, 4) и B(-3, 1).
Для вычисления суммы координат векторов, сложим соответствующие координаты:
A + B = (2 + (-3), 4 + 1) = (-1, 5)
Пример 3: Сумма координат сторон прямоугольника
Допустим, у нас есть прямоугольник со сторонами: AB, BC, CD, DA.
Для вычисления суммы координат каждой стороны, сложим соответствующие координаты точек:
AB = (xB-xA, yB-yA)
BC = (xC-xB, yC-yB)
CD = (xD-xC, yD-yC)
DA = (xA-xD, yA-yD)
где (xA, yA), (xB, yB), (xC, yC), (xD, yD) — координаты точек.
Например, если координаты точек A(1, 1), B(4, 1), C(4, 4) и D(1, 4), то:
AB = (4 — 1, 1 — 1) = (3, 0)
BC = (4 — 4, 4 — 1) = (0, 3)
CD = (1 — 4, 4 — 4) = (-3, 0)
DA = (1 — 1, 1 — 4) = (0, -3)
Пример 4: Сумма координат векторов в трехмерном пространстве
Если мы работаем в трехмерном пространстве, то координаты векторов будут состоять из трех чисел.
Пусть у нас есть векторы A(2, 3, -1) и B(-1, 5, 2).
Чтобы вычислить сумму координат векторов, сложим соответствующие координаты:
A + B = (2 + (-1), 3 + 5, -1 + 2) = (1, 8, 1)
Пример 5: Сумма координат векторов в полярной системе координат
В полярной системе координат векторы задаются радиусом r и углом φ.
Предположим, у нас есть два вектора в полярных координатах: A(r1, φ1) и B(r2, φ2).
Для вычисления суммы координат векторов, сложим радиусы и углы:
A + B = (r1 + r2, φ1 + φ2)
Координатная ось — «фотография» чисел в виде точек на прямой ##
пробa Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось.

Чтобы из любой прямой получить координатную ось ,необходимо выбрать на ней нулевую точку$0$- это будет началом отсчета ;отметитьточку$1$ — определить единичный отрезок(т.е. выбрать масштаб)инарисовать стрелочку в положительном направлении отсчёта .На координатной оси изображается взаимооднозначные соответствия между точками и числами . Например, числу$3$на координатной прямойсопоставляется единственная точка$A$, точке$B$-единственное число$-2$, такое число назвали координатой.
Координатная прямая — это прямая с указанными на ней началом отсчёта O (0) , направлением и единичным отрезком.
пробa Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. Мы будем изучать координатную плоскость с прямоугольной системой координат.
Координаты точек на прямой.
пробa Точка$O$разбиваетпрямую$AB$на два луча$OA$и$OB$ . Если примем точку$O$ за начало отсчета , выберем на ней единичный отрезок и положительное направление , то мы превратим эту прямую в координатную ось .Рассмотрим на ней произвольную точку .Как определить ее положение?Для ответа на этот вопрос придумали понятие — координата . Положение любой точки на координатной осизадается её координатой.Чтобы отличить друг от друга координаты , перед числами на левом луче$OA$условились ставить знак «минус », а перед числами на правом луче$OB$-знак«плюс».

Координатысо знаком»$-$»называются отрицательными.Координатысо знаком «+» называютсяположительными .
Точка$O$- начало отсчета илиначало координат , изображает ноль.Само число$0$не является ни положительным ни отрицательным , только отделяет положительные и отрицательные числа друг от друга .
Координата точки — это число , показывающее положение точки на прямой.

Записывают координаты точек$B$,$C$,$D$следующим образом:$B(-4,2)$,$C\left(-\frac{1}{2}\right)$,$D(3,9)$.
Изображение чисел точками на координатной оси.
Числа на координатной прямой выглядят точками. Для тогочтобыпостроитьточку, соответствующую некоторому числу$a$ , нужно:определить знак этого числа ;от начала координат отложить отрезок , равный$\left|a\right|$вправо , если знак»+»ивлево , еслизнак»-» .
Число$a$в таком случае называют координатой построенной точки .

На рисунке числа $3$, $\frac{1}{4}$,$-0,9$изображены соответсвенно точками$B$,$C$,$D$. Числа- это«адреса»точек на координатной прямой.Точки-это»фотографии» чисел.
Введение оси координат:
1) Выбрать на прямой начало координат;
2) Выбрать положительное направление;
3) Выбрать единичный отрезок.
Координаты точки:
Каждой точке можно присвоить свою координату-это расстояние от точки до начала координат с учетом знака: слева от $0$знак $-$ , справа$+$.
Изображение числа : пробa
По любой координате можно восстановить точку.
Цилиндрическая и сферическая системы координат
Декартова система координат обеспечивает простой способ описания расположения точек в пространстве. Однако некоторые поверхности сложно смоделировать с помощью уравнений, основанных на декартовой системе. Рассмотрим два разных способа описания положения точек в пространстве, оба из которых основаны на расширениях полярных координат. Как следует из названия, цилиндрические координаты полезны для решения задач, связанных с цилиндрами, таких как расчет объема круглого резервуара для воды или количества масла, протекающего по трубе. Точно так же сферические координаты полезны для решения задач, связанных со сферами.
Цилиндрическая система координат
Когда мы расширили традиционную декартову систему координат с двух измерений до трех, мы просто добавили новую ось для моделирования третьего измерения. Начиная с полярных координат, мы можем следовать тому же процессу, чтобы создать новую трехмерную систему координат, называемую цилиндрической системой координат. Таким образом, цилиндрические координаты обеспечивают естественное расширение полярных координат до трех измерений.
В цилиндрической системе координат точка в пространстве (рис. 3) представлена упорядоченными тремя скалярами \ где \ полярные координаты проекции точки на плоскость \, а z-координата в декартовой системе координат.
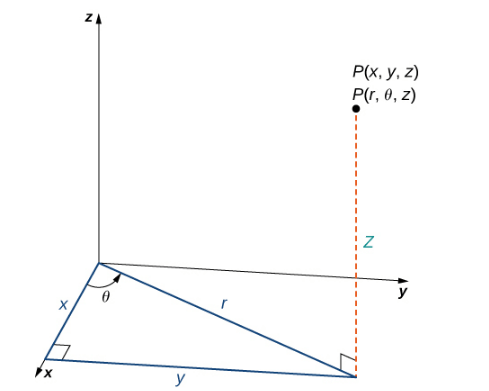 Рис. 3 Правый треугольник лежит в плоскости xy
Рис. 3 Правый треугольник лежит в плоскости xy
Длина гипотенузы равна r и θ — мера угла, образованного положительной осью x и гипотенузой. Г координата описывает местоположение точки выше или ниже х плоскости.
На плоскости xy прямоугольный треугольник, показанный на рис. 3, дает ключ к преобразованию между цилиндрическими и декартовыми (прямоугольными) координатами.
Преобразование между цилиндрическими и декартовыми координатами
Прямоугольные координаты (x,y,z) и цилиндрические координаты (r,θ,z) точки связаны следующим образом:
\
\ — уравнения для преобразования из цилиндрических координат в декартовые
\ и \
\ — уравнения для преобразования из декартовых в цилиндрические
\
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Путаница в системе координат
Когда вы используете систему координат, вы, возможно, слышали много-много псевдонимов. У новичков легко возникнуть сомнения относительно некоторых из наиболее необычных имен. Позвольте мне разобраться с ними здесь.
- Мировые координаты, глобальные координаты, левые координаты, абсолютные координаты
- Местные координаты, собственные координаты, координаты объекта, локальные координаты, относительные координаты
- координаты экрана, координаты пикселей
- координаты области просмотра, координаты окна
- Координаты пользовательского интерфейса, координаты пользовательского интерфейса
Координаты в математике:
Координаты — это числовые значения, которые используются для определения положения точки в пространстве или на плоскости. В математике координаты широко применяются для описания геометрических фигур, решения уравнений и моделирования различных процессов.
Существует два вида координат — прямоугольные (декартовы) и полярные. Прямоугольные координаты определяют положение точки с помощью пары чисел (x, y), где x — это расстояние от точки до вертикальной оси (ось ординат), а y — это расстояние от точки до горизонтальной оси (ось абсцисс). Полярные координаты используются для описания положения точки с помощью радиуса (r) и угла (θ), который образуется между положительным направлением оси абсцисс и линией, соединяющей начало координат и точку.
Декартовы координаты широко используются в геометрии и анализе для определения положения точек на плоскости или в пространстве. С их помощью можно решать уравнения и системы уравнений, описывать прямые, плоскости, кривые и поверхности.
Полярные координаты находят применение в физике, географии, оптике и других областях науки. Они позволяют более удобно описывать криволинейные фигуры, такие как окружности, эллипсы и спирали.
Использование координат позволяет точно определить положение объектов и решать различные задачи, связанные с пространственным размещением и движением. Это важный инструмент для математиков, физиков, программистов и других специалистов, работающих с пространственными данными.
Координаты точки в декартовой системе координат
Для начала поставьте точку М на оси быка. Любое действительное число xM равно единственной точке M, лежащей на этой прямой. В этом случае начало координатных линий всегда равно нулю.
Каждая точка M, которая находится на Ox, равна действительному числу xM. Это действительное число равно нулю, если точка M находится в начале координат, то есть на пересечении Ox и Oy. Если точка удаляется в положительном направлении, длина сегмента положительна, и наоборот.
Число xM — это координата точки M на данной координатной прямой.
Пусть точка является проекцией точки Mx в Ox и My в Oy. Это означает, что через точку M можно провести прямые, перпендикулярные осям Ox и Oy, после чего мы получим соответствующие точки пересечения Mx и My. Тогда точке Mx на оси Ox соответствует номер xM, а My на Oy — yM. Как это отображается на осях координат:
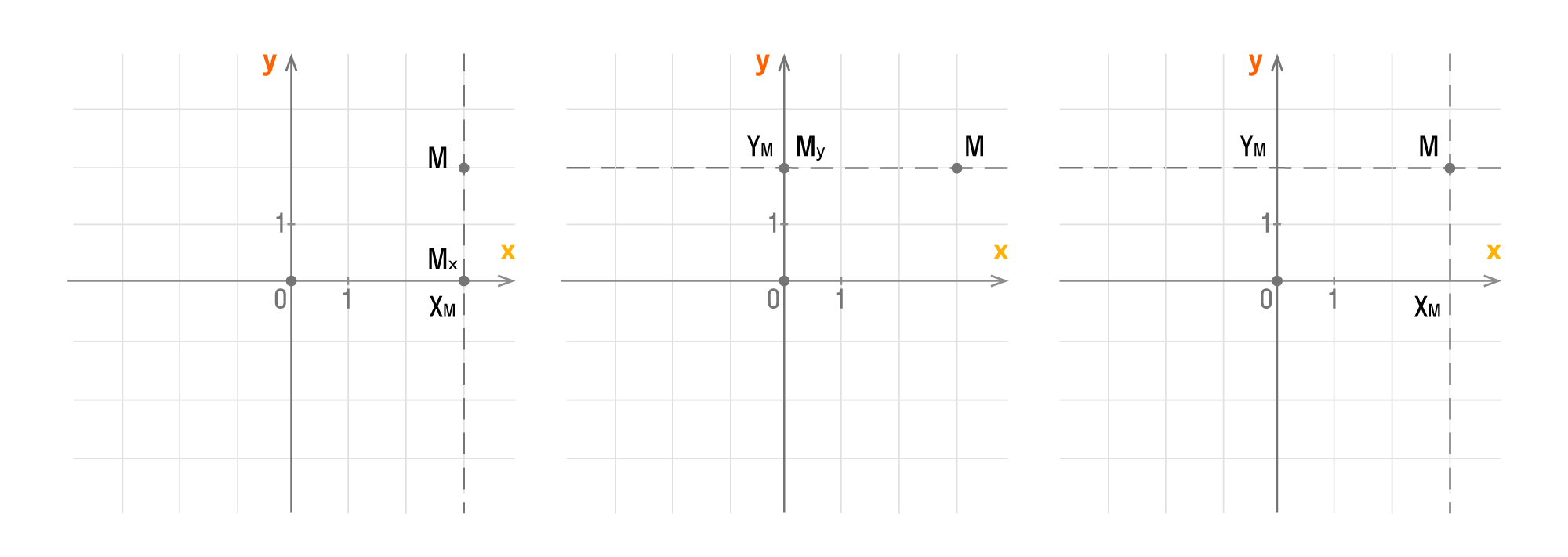
Каждой точке M на данной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса M — xM, ордината M — yM.
верно и обратное: каждой паре (xM, yM) соответствует точка на плоскости.
Линейные координаты: определение и обозначение
В системе линейных координат ось прямой обозначается как линия, на которой располагаются точки. Обычно, чтобы обозначить точку на оси координат, используются две прямоугольные системы, обозначенные как «х» и «у».
Ось «х» обозначает горизонтальное направление, причем точки, расположенные слева от нулевой точки «0» на оси «х», имеют отрицательные значения координат. Точки, расположенные справа от нулевой точки «0» на оси «х», имеют положительные значения координат.
Ось «у» обозначает вертикальное направление, причем точки, расположенные ниже нулевой точки «0» на оси «у», имеют отрицательные значения координат. Точки, расположенные выше нулевой точки «0» на оси «у», имеют положительные значения координат.
Таким образом, «х» и «у» представляют собой значения, которые выражают положение точки на прямой. Зная значения «х» и «у», можно точно определить положение точки в системе линейных координат.
Плоскость, общее уравнение плоскости
Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.
Пусть в пространстве есть три уже известные нам оси координат — Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.
Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:
Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор
перпендикулярен вектору
Вектор
Теперь, используя формулу скалярного произведения векторов
Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости,
Перед решением задач может пригодиться урок о декартовой системе координат. Также хорошо бы владеть материалом о скалярном произведении векторов.
Пример 1. Составить уравнение плоскости, проходящей через точку
Решение. Используем формулу (1), еще раз посмотрим на неё:
В этой формуле числа A , B и C координаты вектора
xyz
Вычисления очень простые: подставляем эти числа в формулу и получаем
Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:
Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида
называется общим уравнением плоскости.
Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.
Как найти эти точки? Чтобы найти точку пересечения с осью Oz , нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0 . Поэтому получаем z = 6 . Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6) .
Точно так же находим точку пересечения плоскости с осью Oy . При x = z = 0 получаем y = −3 , то есть точку B(0; −3; 0) .
И, наконец, находим точку пересечения нашей плоскости с осью Ox . При y = z = 0 получим x = 2 , то есть точку C(2; 0; 0) . По трём полученным в нашем решении точкам A(0; 0; 6) , B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.
Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.
1. При D = 0 уравнение
2. При A = 0 уравнение
Ox
OxOxB =
OyC =
Oz
3. При A = D = 0 уравнение
OxOxA =D =
Oy
Oz
4. При A = B = 0 уравнение
xOyOxAOyB
yOz
xOz
5. При A = B = D = 0 уравнение
z =xOyxOyA = B =D =y =xOzx =yOz
Пример 3. Составить уравнение плоскости P , проходящей через ось Oy и точку
Решение. Итак, плоскость проходит через ось Oy . Поэтому в её уравнении y = 0 и это уравнение имеет вид
AC
P
Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (
Среди них x = 2 , z = 3 . Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:
Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем
Подставив найденное значение A в уравнение
Это и есть уравнение, требуемое в условии примера.
Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение
Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением
Деление отрезка в заданном отношении.
Найдем координаты точки \(M\) на отрезке \(AB\), которая делит этот отрезок в отношении \(\lambda/\mu\), то есть удовлетворяет условию
$$
\frac{|AM|}{|MB|} = \frac{\lambda}{\mu},\ \lambda > 0,\ \mu > 0\nonumber
$$
(рис. 2.3). Это условие можно переписать в виде
$$
\mu\overrightarrow{AM} = \lambda\overrightarrow{MB}.\label{ref1}
$$
Рис. 2.3
Обозначив через (\(x_{1}\), \(y_{1}\), \(z_{1}\)) и (\(x_{2}\), \(y_{2}\), \(z_{2}\)) соответственно координаты точек \(A\) и \(B\), а через (\(x\), \(y\), \(z\)) координаты точки \(M\), разложим обе части равенства по базису, причем компоненты векторов \(\overrightarrow{AM}\) и \(\overrightarrow{MB}\) найдем по . Тогда
$$
\mu(x-x_{1}) = \lambda(x_{2}-x),\ \mu(y-y_{1}) = \lambda(y_{2}-y),\ \mu(z-z_{1}) = \lambda(z_{2}-z).\nonumber
$$
Из этих равенств можно найти \(x\), \(y\) и \(z\), поскольку \(\lambda + \mu \neq 0\):
$$
x = \frac{\mu x_{1} + \lambda x_{2}}{\lambda + \mu},\ y = \frac{\mu y_{1} + \lambda y_{2}}{\lambda + \mu},\ z = \frac{\mu z_{1} + \lambda z_{2}}{\lambda + \mu}\label{ref2}
$$
Если в формулах \eqref{ref2} мы будем считать одно из чисел \(\lambda\) или \(\mu\) отрицательным, то из равенства \eqref{ref1} увидим, что \(M\) находится на той же прямой вне отрезка \(AB\), деля его в отношении |\(\lambda/\mu\)|. Поэтому из формул \eqref{ref2} можно найти координаты точки, делящей отрезок в заданном отношении как внутренним, так и внешним образом.
На плоскости и на прямой линии задача о делении отрезка решается точно так же, только из трех равенств в \eqref{ref2} остается соответственно два и одно равенство.




























