Алгебра

Рациональные числа на координатной прямой

Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:

На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.

Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.

Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.

Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей

Попробуем понять, почему дробь  вдруг расположилась между нулём и единицей.

Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину

Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.

Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5

Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.

Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и  равна 0,5

А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь

Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2

Значение дроби равно 1,5

Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:

Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.

Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.

Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.

Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.

К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2

Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:

Пример 3. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться очень близко к нулю

Значение дроби равно 0,02

Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число

Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.

Пример 4. Отметим на координатной прямой рациональное число 0, (3)

Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная

0,33333….и так далее до бесконечности..

И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.

Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3

Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.

Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3

это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.

Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь

Значение дроби равно 2,5

Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:

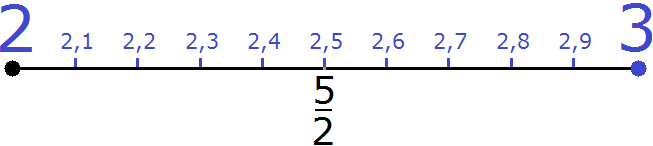
Видно, что наше рациональное число  расположилось там же, где и десятичная дробь 2,5

Понятие и характеристика

Огромным прорывом в математической науке стали числа, которые называются иррациональными. Какие-либо ограничения, связанные с целыми величинами или обыкновенными дробями, были сняты. Люди получили возможность открывать и даже изобретать новые количественные значения.

Иррациональным считается вещественное число, не являющееся рациональным. Оно не может быть представлено в виде арифметической дроби n/m, где числитель и знаменатель являются целыми величинами, а n не равно 0. Также подобные значения невозможно точно выразить целой величиной. Это значит, что иррациональные числа всегда выглядят, как бесконечные непериодические десятичные дроби. Для их обозначения применяют радикалы или специальные буквы, например, е, π. Множество чисел обозначается заглавной буквой в полужирном начертании без заливки.

Не всякая величина из множества значений, не относящихся к рациональным, так известна, как число π. В школьной программе его часто определяют, как 3,14, но истинный показатель π значительно ближе к 3. Следует отметить, что даже известная длинная десятичная дробь является лишь приближённым вариантом, поскольку указанное число нельзя точно установить. Дробь, которую используют для этого, бесконечна, а цифры в ней распределяются без какой-либо закономерности.

Самыми известными примерами таких иррациональных чисел являются:

• γ — постоянная Эйлера — Маскерони;
• ζ(3) — постоянная Апери;
• φ — золотое сечение;
• α, δ — постоянные Фейгенбаума;
• e — число;
• π — число Пи;
• ψ — сверхзолотое сечение.

Зачастую понять, что число иррационально, можно по его соответствию одному из перечисленных признаков:

• квадратный корень для любого натурального n, которое не является точным квадратом;
• e в степени x для любого рационального x, не равного 0;
• ln x для любого положительного рационального x, который не равен 1;
• π и π в степени n для любого целого n, не равного 0.

Но в ряде случаев установить иррациональность значения возможно только посредством доказательства. К примеру, школьникам часто дают задание доказать, что число log3 4 не относится к рациональным.

Правило извлечения квадратного корня из натурального числа

Пусть нужно извлечь квадратный корень из натурального числа
, причем известно, что корень извлекается. Чтобы найти результат, иногда удобно воспользоваться следующим правилом.

• Разобьем число
  на грани (справа налево начиная с последней цифры), включив в каждую грань по две рядом стоящие цифры. При этом следуетучесть, что если состоит из четного числа цифр, то в первой (слева) грани будет две цифры; если же число
  состоит из нечетного числа цифр, то первая грань состоит из одной цифры. Количество граней показывает, сколько цифр содержит целая часть числа .
• Подбираем наибольшую цифру такую, что ее квадрат не превосходит числа, находящегося в первой грани; эта цифра — первая цифра числа .
• Возведем первую цифру результата в квадрат, вычтем полученное число из первой грани, припишем к найденной разности справа вторую грань. Получится некоторое число А. Удвоив имеющуюся часть результата, получим число . Теперь подберем такую наибольшую цифру х, чтобы произведение числа
  на х не превосходило числа А. Цифра х —вторая цифра результата, т. е. искомого числа .
• Произведение числа
  на х вычтем из числа А, припишем к найденной разности справа третью грань, получится некоторое число В. Удвоив имеющуюся часть результата, получим число . Теперь подберем такую наибольшую цифру у, чтобы произведение числа
  на у не превосходило числа В. Цифра у — третья цифра результата.

Следующий шаг правила повторяет 4-й шаг. Это продолжается до тех пор, пока не используется последняя грань.

Пример 1

Вычислить

Решение:

Разобьем число на грани: 13’83’84. Получили три грани, значит, в результате должно получиться трехзначное число. Первая цифра результата 3, так как
Вычтя 9 из 13, получим 4. Приписав к 4 следующую грань, получим А = 483. Удвоив имеющуюся часть результата, т. е. число 3, получим
= 6. Подберем теперь такую наибольшую цифру х, чтобы произведение двузначного числа
т. е.
на х было меньше числа 483. Такой цифрой будет 7, так как
— это меньше 483, а
— это больше 483. Итак, вторая цифра результата 7.

Вычтя 469 из 483, получим 14. Приписав к этому числу справа последнюю грань, получим
= 1484. Удвоив имеющуюся часть результата, т. е. число 37, получим В = 74. Подберем теперь такую наибольшую цифру у, чтобы произведение трехзначного числа
, т. е.
, на у не превосходило 1484. Такой цифрой будет 2, так как
. Цифра 2 — последняя цифра результата. В ответе получили 372.

Пример 2

Вычислить

Решение:

Если корень не извлекается, то после последней цифры заданного числа ставят запятую и образуют дальнейшие грани, каждая из которых имеет вид 00. В этом случае процесс извлечения корня бесконечен; он прекращается, когда достигается требуемая точность.

Интересные факты

А известно ли вам о существовании фан-клуба, где поклонники этого загадочного математического феномена ищут все новые сведения о Пи, пытаясь разгадать его тайну. Членом этого клуба может сталь любой человек, который знает наизусть определенное количество чисел Пи после запятой;

А знаете ли вы, что в Германии под охраной ЮНЕСКО находится дворец Кастадель Монте, благодаря пропорциям которого можно вычислить Пи. Целый дворец посвятил этому числу король Фридрих II.

Оказывается, число Пи пытались использовать при строительстве Вавилонской башни. Но к превеликому сожалению, это привело к краху проекта, так как на тот момент было недостаточно изучено точное исчисление значения Пи.

Певица Кейт Буш в своем новом диске записала песню под названием «Пи», в которой прозвучало сто двадцать четыре числа из знаменитого числового ряда 3, 141…..

Определение и примеры иррациональных чисел

При изучении десятичных дробей мы отдельно рассмотрели бесконечные непериодические десятичные дроби. Такие дроби возникают при длин отрезков, несоизмеримых с единичным отрезком. Также мы отметили, что бесконечные непериодические десятичные дроби не могут быть переведены в обыкновенные дроби (смотрите перевод обыкновенных дробей в десятичные и обратно), следовательно, эти числа не являются рациональными числами , они представляют так называемые иррациональные числа.

Так мы подошли к определению иррациональных чисел
.

Определение.

Числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби, называются иррациональными числами
.

Озвученное определение позволяет привести примеры иррациональных чисел
. Например, бесконечная непериодическая десятичная дробь 4,10110011100011110000…
(количество единиц и нулей каждый раз увеличивается на одну) является иррациональным числом. Приведем еще пример иррационального числа: −22,353335333335…
(число троек, разделяющих восьмерки, каждый раз увеличивается на две).

Следует отметить, что иррациональные числа достаточно редко встречаются именно в виде бесконечных непериодических десятичных дробей. Обычно они встречаются в виде , и т.п., а также в виде специально введенных букв. Самыми известными примерами иррациональных чисел в такой записи являются арифметический квадратный корень из двух , число «пи» π=3,141592…
, число e=2,718281…
и золотое число .

Иррациональные числа также можно определить через действительные числа , которые объединяют рациональные и иррациональные числа.

Определение.

Иррациональные числа
– это действительные числа, не являющиеся рациональными.

Геометрическое изображение вещественных чисел

Изображение вещественных чисел точками на координатной прямой

Введем ряд предварительных понятий. Рассмотрим произвольную прямую. На ней можно указать два взаимно противоположных направления. Выберем одно из них и на рисунке будем обозначать его стрелкой (рис. 1). Пусть, кроме того, выбрана масштабная единица для измерения длин отрезков. Прямая с выбранным на ней направлением называется осью.

Рассмотрим на оси две произвольные точки Л и В. Отрезок с граничными точками Л и В будем называть направленным, если указано, какая из точек Л и В считается началом, а какая — кон- концом отрезка. Направленный отрезок с началом в точке А и концом в точке В обозначим и будем считать, что он направлен от начала к концу. Отметим, что в записи буква, обозначающая начало направленного отрезка, пишется первой, а буква, обозначающая его конец, — второй. Длина направленного отрезка обозначается так:

Для направленных отрезков, лежащих на оси (или параллель- параллельных оси), вводится понятие величины направленного отрезка. Величиной АВ направленного отрезка называется число, равное , если направления отрезка и оси совпадают, и равное — , если эти направления противоположны. Для отрезков изображенных на рис. 2,

Заметим, что величины направленных отрезков при любом направлении оси отличаются знаками: Если точки А и В совпадают, то величину направленного отрезка будем считать равной нулю.

Для любых трех точек А, В и С на оси справедливо равенство АВ + ВС = АС, которое назовем основным тождеством (в дальнейшем оно неоднократно используется).

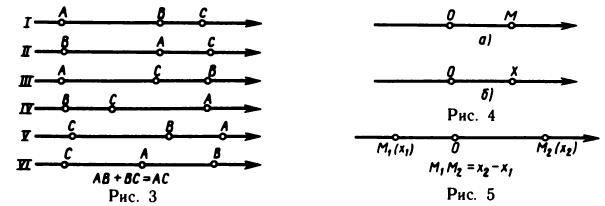
Справедливость основного тождества легко устанавливается из рисунка, но при этом нужно рассмотреть различные случаи взаимного расположения точек А, В и С на оси. Если все три точки А, В и С различны, то таких случаев шесть (рис. 3). В каждом из этих случаев основное тождество проверяется элементарно.

Перейдем теперь к геометрическому изображению вещественных чисел. Рассмотрим какую-нибудь прямую. Выберем на ней направление (тогда она станет осью) и некоторую точку О (начало координат). Прямую с выбранным направлением и началом координат назовем координатной прямой (считаем, что масштабная единица выбрана). Пусть М — произвольная точка на прямой (рис. 4, а).

Поставим в соответствие точке М число х, равное величине ОМ направленного отрезка Число х называется координатой точки М. Тем самым каждой точке координатной прямой будет соответствовать определенное вещественное число — ее координата. Справедливо и обратное: каждому вещественному числу х соответствует некоторая точка на координатной прямой, а именно такая точка М, координата которой равна х.

Таким образом, вещественные числа можно изображать точками на координатной прямой. Поэтому около точки на координатной прямой часто указывают число —ее координату (рис. 4, б).

Пусть точка имеет координату , а точка — координату (рис. 5.). Выразим величину направленного отрезка через координаты точек и . Согласно основному тождеству откуда поэтому Эту формулу будем часто использовать в аналитической геометрии.

Некоторые наиболее употребительные числовые множества

Пусть а и b — два числа, причем а<b. Будем пользоваться cледующими обозначениями: 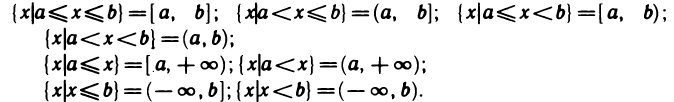Множество всех вещественных чисел будем обозначать так:

Все эти множества называются промежутками, причем — отрезок (сегмент), —полуинтервалы, а — интервалы. Промежутки называются конечными; а и b называются их концами. Остальные промежутки называются бесконечными.

Числовым промежуткам соответствуют промежутки на координатной прямой. Например, сегмент изображается на координатной прямой отрезком таким, что точка имеет rоординату , а точка —координату (рис. 5). Изображением множества всех чисел служит вся координатная пря- прямая. Поэтому множество называется также числовой прямой, а любое число — точкой этой прямой. Пусть а —произвольная точка числовой прямой и — положительное число. Интервал называется -окрестностью точки а.

Метод математической индукции в доказательстве иррациональных чисел

Чтобы использовать метод математической индукции для доказательства иррациональности числа, обычно применяют следующий шаги:

1. Показать, что утверждение выполняется для базового случая. В контексте иррациональных чисел, это означает показать, что число не может быть представлено в виде дроби с целыми числами в числителе и знаменателе.
2. Предположить, что утверждение выполняется для некоторого натурального числа k. То есть, предполагается, что число имеет иррациональное представление при n = k.
3. Доказать, что утверждение также выполняется для следующего натурального числа k + 1. То есть, показать, что число имеет иррациональное представление при n = k + 1, исходя из предположения об иррациональности при n = k.

С помощью этих шагов можно установить иррациональность числа для всех натуральных чисел и, следовательно, доказать, что число является иррациональным.

Пример доказательства иррациональности числа √2 с использованием метода математической индукции:

1. Базовый случай: При n = 1 число 2 не может быть представлено в виде дроби с целыми числами в числителе и знаменателе, так как его квадратный корень является иррациональным.
2. Предположим, что √2 является иррациональным для некоторого натурального числа k.
3. Докажем, что √2 является иррациональным для n = k + 1. Предположим, что √2 может быть представлено в виде дроби p/q, где p и q — целые числа без общих делителей, включая делители -1 и 1. Тогда:

√2 = p/q

2 = (p/q)²

2q² = p²

Таким образом, p² должно быть четным числом, а значит, p также должно быть четным числом (если p было бы нечетным, то p² было бы нечетным). Пусть p = 2m, где m — некоторое целое число.

2q² = (2m)² = 4m²

q² = 2m²

Таким образом, q² должно быть четным числом, а значит, q также должно быть четным числом.

Из условия «p и q — целые числа без общих делителей, включая делители -1 и 1» следует, что и p, и q должны быть четными числами, тогда q/2 и p/2 также являются целыми числами без общих делителей.

Теперь можно переписать равенство √2 = p/q в следующем виде:

√2 = (p/2) / (q/2)

Это означает, что √2 может быть представлено в виде дроби с целыми числами в числителе и знаменателе, что противоречит исходному условию. Значит, предположение об иррациональности √2 при n = k + 1 верно.

Таким образом, с использованием метода математической индукции можно доказать, что число √2 является иррациональным.

Рациональные числа и их свойства.

Рациональное число — такое число, которое можно записать в виде p/q, где p — целое число, q — натуральное число. В частности, любое целое число является рациональным, поскольку его можно записать в виде p = p/1. Например, 0 = 0/1, 1=1/1.

Пусть a = p/q, b = p₁/q₁ — два рациональных числа. Тогда правило упорядочения этих чисел определяется так:

• если pq₁ = qp₁, то a = b;
• если pq₁ > qp₁, то a > b;
• если pq₁ < qp₁, то a < b;

а сумма и произведение чисел a и b определяется равенствами

$$a+b=\frac{pq_1+qp1}{qq_1}, \ ab=\frac{pp_1}{qq_1}\nonumber$$

Операции сложения и умножения рациональных чисел обладают свойствами:

• коммутативности:$$a+b=b+a, \ ab=ba\nonumber$$
• ассоциативности:$$(a+b)+c=a+(b+c), \ (ab)c=a(bc)\nonumber$$
• дистрибутивности:$$a(b+c)=ab+ac\nonumber$$
• для любого рационального числа a справедливы неравенства$$a+0=a, \ a\cdot1=a\nonumber$$

Операции вычитания и деления вводятся как обратные соответственно к операциям сложения и умножения:

• (для любых рациональных чисел a, b существует (и притом единственное) число x такое, что$$b+x=a\nonumber$$это число называют разностью чисел a и b и обозначают a — b).
• если b ≠ 0, то существует единственное число z такое, что$$bz=a\nonumber$$это число называют частным чисел a и b и обозначают a/b.

Отметим еще основные свойства неравенств для рациональных чисел:

• если a > b и b > c, то a > c (транзитивность);
• если a > b, то a + c > b +c при любом c;
• если a > b и c > d, то a + c > b + d;
• если a > b и c > 0, то ac > bc;
• если a > b и c < 0, то ac < bc.

В дальнейшем, мы будем использовать следующие обозначения:

• \(\mathbb{N}\) — множество натуральных чисел;
• \(\mathbb{Z}\) — множество целых чисел;
• \(\mathbb{Q}\) — множество рациональных чисел.

В множестве \(\mathbb{Q}\) можно выполнять не только четыре арифметических действия, но и решать уравнения и системы уравнений первой степени. Однако, даже простейшие квадратные уравнения вида x2=a, где \(a\in\mathbb{N}\), не всегда разрешимы в множестве \(\mathbb{Q}\). Так например, уравнение x2=3 не имеет решений в множестве рациональных чисел \(\mathbb{Q}\).

Докажем, что решение данного уравнения \(\sqrt{3}\) не является рациональным числом.

Давайте предположим противное, то есть что \(\sqrt{3}\) — рациональное число

Тогда по определению рациональных чисел можем записать его как несократимую (и это важно) дробь, то есть:
$$
\sqrt{3}=\frac{p}{q},\qquad p\in\mathbb{Z}, \ q\in\mathbb{N}\nonumber
$$
Возведем обе части в квадрат и преобразуем дробь. Получаем
$$
p^2=3q^2\nonumber
$$
Как видно из выражения, p2 делится на 3 без остатка

Если записать это «по-умному», то
$$
p^2 \ \equiv \ 0 \ (\operatorname{mod} \ 3)\nonumber
$$
Но это означает, что также и само p2 делится на три без остатка. В самом деле, любое натуральное число можно разложить на простые множители. Запишем p следующим образом:
$$
p=p_0^{x_0}\cdot p_1^{x_1}\cdot\ldots\cdot p_n^{x_n}\nonumber
$$
, где \(p_0,p_1,\ldots ,p_n\) — простые числа, а \(x_0,x_1,\ldots,x_n\) — целые числа).

Тогда p2 можно записать так:

$$
p^2=p_0^{2x_0}\cdot p_1^{2x_1}\cdot\ldots\cdot p_n^{2x_n}\nonumber
$$
Поскольку p2 делится на 3 целиком, то это значит, что в нашем разложении какое-то p_i = 3. А поскольку множество всех p_i (i лежит в пределах от 0 до n включительно) образует множество всех делителей исходного p, то 3 также является делителем p. То есть мы можем записать, что:
$$
p=3\cdot k,\qquad k\in\mathbb{N}\nonumber
$$
То есть, если вернемся к одному из первых утверждений и заменим наше p, то получим:
$$
9\cdot k^2=3\cdot q^2\quad\Leftrightarrow\quad q^2=3\cdot k^2\nonumber
$$
Повторяя вышеизложенные рассуждения, получим, что q так же делится на 3, как и p. Предположим, что:
$$
q=3\cdot m,\qquad m\in\mathbb{N}\nonumber
$$
Таким образом:
$$
\frac{p}{q}=\frac{3\cdot k}{3\cdot m}=\frac{k}{m},\nonumber
$$
что противоречит первоначальному утверждению, что p/q — несократимая дробь. Следовательно, \(\sqrt{3}\) не является рациональным. \(\bullet\)

Таким образом, уже проблема решения простых уравнений типа x2=a, x3=a, где \(a\in\mathbb{N}\), приводит к необходимости расширения множества рациональных чисел \(\mathbb{Q}\) путем добавления к этому множеству новых элементов, называемых иррациональными числами.

Иррациональные числа

Иррациональное число — это действительное число, которое нельзя записать в виде простой дроби:

  1,5 рационально, но π иррационально

Иррациональное означает

Давайте посмотрим, что делает число рациональным или иррациональным…

Рациональные числа

A Rational Число можно записать как 0003 Отношение двух целых чисел (т.е. простой дроби).

Пример: 1,5 является рациональным, поскольку его можно записать как отношение 3/2

Пример: 7 рационально, потому что его можно записать как отношение 7/1

Пример 0,333. .. (3 повторения) также является рациональным, поскольку его можно записать как отношение 1/3

Но некоторые цифры нельзя записать как отношение двух целых чисел…

…их называют Иррациональные Числа .

Пример:

π (Pi)

π  = 3,1415926535897932384626433832795… (и больше)

Мы не можем s записать простую дробь, которая равна Пи.

Популярное приближение 22 / ₇ = 3,1428571428571… близко, но неточное .

Еще одна подсказка заключается в том, что десятичная дробь продолжается вечно, не повторяясь.

Не может быть записан как дробь

Это иррационально потому что его нельзя записать как отношение (или дробь), не потому что это безумие!

Таким образом, мы можем определить, является ли число рациональным или иррациональным, попробовав записать число в виде простой дроби.

Пример:

9,5

9,5 = 19 2

Итак, это рациональное число (и поэтому не иррациональное )

Вот еще несколько примеров:

Как дробь
 
Рациональное или Иррациональное?
1,75
 
7 4

 
Рационал

.001
 
1 1000

 
Рационал

√2 (квадратный корень из 2)
 
?
 
Неразумно !

Квадратный корень из 2

Давайте посмотрим на квадратный корень из 2 более внимательно.

Ответ: квадратный корень из 2 , который равен 1.4142135623730950…(и т.д.)

… на самом деле мы не может записать квадратный корень из 2, используя отношение двух чисел…

… (вы можете узнать , почему , на странице «Иррационально ли это?»)…

… и так мы знаем это иррациональное число .

Но √4 = 2 рационально, а √9 = 3 рационально.

… так что не все корни иррациональны.

Примечание по умножению иррациональных чисел

Взгляните на это:

• π × π = π 2 известно, что иррационально
• Но √2 × √2 = 2 равно рациональному

Так что будьте осторожны… умножение иррациональных чисел может дать рациональное число!

Забавные факты….

По-видимому Гиппас (один из учеников Пифагора) открыл иррациональные числа при попытке записать квадратный корень из 2 в виде дроби (считается, что с помощью геометрии). Вместо этого он доказал квадратный корень из 2·9.0093 нельзя было записать в виде дроби, поэтому иррационально .

Но последователи Пифагора не могли принять существование иррациональных чисел, и говорят, что Гиппас был утоплен в море в наказание богов!

434 435 1064 2022 3987 1065 3988 2023 2990 2991

Класс и характеристика действительных чисел

Все действительные значения чисел можно представить по следующей классификации:

простое натуральное значение или целое числовое значение — это простые числовые значения, которые возникают при простом и естественном счете. В технических науках множество целых числовых значений принято обозначать символом Z.

Любое значение множества натуральных чисел N — это, значение   подмножеств целых числовых значений, которые обозначаются буквой  Z .

Целым вполне возможно назвать, любое число натурального значения. Однако, целое число не всегда будет является натуральным числом, и это следует всегда помнить.

Натуральные числа, можно определить двумя методами:

значения, которые возникают, при подсчете определенных предметов, которые являются числительными (первый день, четвертый урок, третий ребенок);

обозначение конкретных событий или простых предметов (три слова, пять рулонов).

В первом случае нумерация начинается с единичного значения, а для второго характерен подсчет, с нулевого знака.

положительное и отрицательное дробное значение, любого вида;

Простое положительное число — это как правило число, которое располагается с правой стороны от нулевого значения. Ему присвоен знак плюс, иными словами числа с плюсовым значением.

Например: 1;15;36;12356.  

Рассмотрим значение   15 — целое число со знаком плюс, то есть положительное значение. На координатной прямой оно располагается справа от нулевого значения или точки первоначального отсчета.  

Отрицательное число — это данное определение идентично вышеуказанному положительному, за исключение левой стороны от нулевого значения и знак меняется с плюса на минус.

Примеры целых отрицательных чисел: − 52 ,   − 258 ,   − 1 -528, -2568, -1. Нулевое значение делит между собой  положительные и отрицательные целые числа.  В тоже время оно, является ни положительным и ни отрицательным Числовое значение, которое является обратным каждому отрицательному значению, следовательно, является положительным целым числом.  

Сравнивая с нулевым значением, можно сформулировать и другие определения, конкретно опираясь на ноль.

Например: числа, которые являются меньше нуля, можно назвать отрицательными целыми числовыми значениями.

Числа, которые больше нулевого данного числа, будет называться простыми положительными значениями. Положительные данные, находящиеся правее от нулевого числового значения, следовательно, отрицательные мы увидим слева от нуля. Мы уже рассмотрели и изучили правило, что натуральные числа — это целый ряд или подмножество целых значений. Рассмотрим это подробнее. Несколько данных натуральных чисел объединяют в себя целые положительные значения. Из этого следует, что множество отрицательных целых значений числа, может быть представлено, как множество значений, с обратным значением знака к натуральным числам

 Стоит уделить внимание следующему понятию!

Любое натуральное число значение, может иметь свойство целого значения, однако, не каждое целое значение может быть натуральным. Отвечая на популярный вопрос, можно смело ответить — что являться не могут.

Дадим определения таким значениям неотрицательные и не положительные.

Неотрицательные целые числа — это положительные числа и нулевое числовое значение.

Неположительные целые числа — это отрицательные целые числа и значение равное нулю.

Как мы уже говорили ранее числовое данное равное нулю, не относится ни к какому из изученных натуральных значений. Простыми примерами неотрицательных чисел могут быть следующие значения: 45; 142; 26589;105689.

В свою очередь -52; -5698; -12598 это неположительные значения. Также есть смешанные значения, и дроби десятичного значения, они бывают:

1. положительные;
2. отрицательные;
3. периодические;
4. бесконечные;
5. непериодические.

Выразить действительные числа, можно в следующем виде:

• корни числа;
• степенное значение;
• логарифмическое;
• сумма;
• разность;
• произведение;
• деление.

Применяя все перечисленные свойства числа действительного типа, можно составлять различного вида математические примеры, уравнения, тригонометрические и алгебраические функции. Составим и запишем несколько примеров решения:

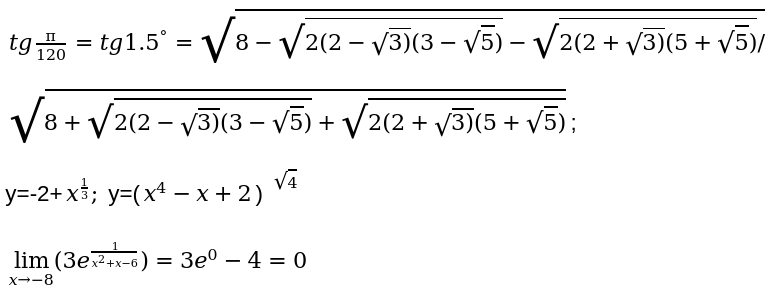
Специальные числа: Пи, e[править]

Наиболее часто встречаются такие константы (то есть постоянные) как π{\displaystyle \pi }, e. Эти два числа получили широкое применение в различных областях математики и физики и поэтому заслуживают отдельного внимания.

Торт с числом Пи

Число Пи — это отношение длины окружности к её диаметру. При этом такое отношение не зависит от размера самой окружности и постоянно для любых окружностей. Обозначение Пи появилось из первой буквы греческого слова «периферия» (окружность). Значение числа Пи выражается бесконечной и непериодической десятичной дробью, поэтому данное число является иррациональным. первые несколько знаков после запятой числа Пи выглядят так 3,141592653589…{\displaystyle 3,141592653589…} В наше время мощные современные компьютеры могут найти данное число с точностью до миллиона и более знаков после запятой. Однако в древности эти знаки приходилось находить на практике с помощью построений, например, вписывая и описывая в данную окружность правильные многоугольники и увеличивая число их сторон. В этом случае длина окружности была заключена между длинами описанного и вписанного многоугольника. Также значение числа Пи математики пытались найти, используя его разложение в виде бесконечных числовых рядов или произведений дробей. Например, Готфрид Вильгельм Лейбниц в 1674 г. установил следующую формулу:
π4=1−13+15−17+…{\displaystyle \pi /4=1-1/3+1/5-1/7+…}. Однако данный ряд сходится очень медленно, поэтому на практике для нахождения точных знаков после запятой мало применим.

Число e выражается следующей бесконечной непериодической десятичной дробью 2,718281828459… Число е равно пределу числовой последовательности при неограниченном росте n, то есть
e=limn→∞(1+1n)n{\displaystyle e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}}
Обозначение e ввел Леонард Эйлер в 1736 году. Он также вычислил первые 23 знака этого числа.

Число e{\displaystyle e} иррациональное и трансцендентное. Доказательство трансцендентности впервые привел французский математики Шарль Эрмит в 1873 году. Также число е играет огромную роль в математическом анализе и теории функций. Если рассмотреть показательную функцию с основанием е (её называют экспонентной ex{\displaystyle e^{x}}, то у такой функции значение производной будет совпадать с самой функцией. (ex)′=ex{\displaystyle (e^{x})’=e^{x}}

Также если рассмотреть логарифм с основанием е, то такой логарифм будет называться натуральным логарифмом.