Рациональные числа: определение, свойства и примеры

Свойства чисел с плавающей точкой

1. В нормализованном виде любое отличное от нуля число представимо в единственном виде. Недостатком такой записи является тот факт, что невозможно представить число 0.
2. Так как старший бит двоичного числа, записанного в нормализованной форме, всегда равен 1, его можно опустить. Это используется в стандарте IEEE 754.
3. В отличие от целочисленных стандартов (например, integer), имеющих равномерное распределение на всем множестве значений, числа с плавающей точкой (double, например) имеют квазиравномерное распределение.
4. Вследствие свойства 3, числа с плавающей точкой имеют постоянную относительную погрешность (в отличие от целочисленных, которые имеют постоянную абсолютную погрешность).
5. Очевидно, не все действительные числа возможно представить в виде числа с плавающей точкой.
6. Точно в таком формате представимы только числа, являющиеся суммой некоторых обратных степеней двойки (не ниже -53). Остальные числа попадают в некоторый диапазон и округляются до ближайшей его границы. Таким образом, абсолютная погрешность составляет половину величины младшего бита.
7. В формате double представимы числа в диапазоне .

Определение полуразности

Полуразность находит применение во многих областях знания. Она используется в философии для анализа понятий, в лингвистике для изучения семантики слов и фраз, и в психологии для изучения категоризации и ассоциаций. Принципы полуразности также применяются в информационных технологиях, в частности, в алгоритмах машинного обучения и распознавания образов.

Основные характеристики полуразности: частичное совпадение, отсутствие полного совпадения, взаимосвязь между понятиями, общность содержания. Полуразность не является абсолютным понятием, и ее интерпретация может различаться в зависимости от контекста и целей исследования.

Понятие и основные характеристики

Основная идея полуразности состоит в том, что она определяет схожесть или различие между объектами или понятиями. При этом полуразность является относительной и может быть интерпретирована по-разному в разных контекстах.

Полуразность может быть применена в различных областях знания, включая философию, психологию, социологию и другие. Это понятие позволяет анализировать отношения между объектами и классифицировать их согласно их схожести.

Основными характеристиками полуразности являются:

• Субъективность — восприятие полуразности может зависеть от контекста, в котором она используется, и от субъективного мнения наблюдателя.
• Относительность — полуразность может быть интерпретирована по-разному в разных контекстах и относительно разных критериев.
• Классификация — полуразность позволяет классифицировать объекты на основе их схожести или различия.
• Контекстуальность — полуразность должна рассматриваться в контексте, учитывая специфические особенности объектов и понятий, которые она описывает.

В итоге, понятие полуразности является инструментом для анализа отношений между объектами и позволяет систематизировать знания в различных областях.

Примеры полуразности

Пример 2: Еще одним примером полуразности может служить понятие «городская сельская местность». Оно описывает зону, которая находится на пересечении городской и сельской окружающей среды. В этой зоне можно наблюдать признаки и города, и сельской местности, но они не являются полностью противоположными друг другу.

Пример 3: Полуразность можно использовать и в более абстрактных понятиях. Например, понятие «историческая современность» описывает период времени, который находится между прошлым и будущим. Этот период характеризуется как аспектами прошлого, так и современности, а значит, можно говорить о полуразности данного понятия.

Пример 4: В музыке также можно встретить примеры полуразности. Например, понятие «мажорно-минорная тональность» описывает состояние, когда мажорная тональность переходит в минорную или наоборот. Это некий переходный момент, который можно назвать полуразностью.

Пример 5: Полуразность можно использовать для описания состояний человека или его эмоций. Например, понятие «серьезно-шуточный» описывает состояние, когда человек смешивает серьезность и юмор. Это некое среднее состояние, которое можно назвать полуразностью.

Полуразность чисел: основные аспекты

Полуразность — это один из числовых параметров, который получается при вычитании из большего числа меньшего и деления полученного значения на среднее арифметическое между этими числами. Другими словами, полуразность — это отношение разницы между двумя числами к среднему арифметическому.

При расчете полуразности можно использовать любые числа. Но для удобства и понимания этого числового параметра, рассмотрим примеры:

• Разность между 8 и 4 равна 4. Среднее арифметическое между ними равняется 6. Таким образом, полуразность между этими числами будет равняться 0,67.
• Разность между 22 и 16 равна 6. Средний арифметический между ними равняется 19. Таким образом, полуразность между числами 22 и 16 равна 0,32.

Полуразность может быть положительной или отрицательной, в зависимости от того, какое число больше. Если первое число больше, то полуразность будет положительной, а если второе число больше, то полуразность будет отрицательной.

Полуразность может использоваться как в теории чисел, так и в практической жизни, например, в экономике и финансах для расчета изменения цен на товары и услуги.

Математические действия с разностью чисел

Чтобы узнать разность чисел, нужно совершить такое арифметическое действие как вычитание, в результате которого по одному данному слагаемому и данной сумме можно найти другое слагаемое.

Вычитание принято обозначать знаком «–» (минус).

Примечание

Обычно вычитание натуральных чисел возможно только в том случае, если уменьшаемое больше вычитаемого. Однако если уменьшаемое меньше вычитаемого, то значение разности получается отрицательным.

Следует привести некоторые особенности действий с нулем:

1. Прибавление к числу нуля не изменяет этого числа.

   Пример

   20+0=20

2. Если первое слагаемое равно второму, то их разность равна нулю.

   Пример

   150-150=0.

Необходимо также обозначить свойства вычитания:

1. x-(y+z)=x-y-z: 26-(14+4)=26-4-14=22-14=8.
2. (x+y)-z=(x-z)+y=x+(y-z): (37+28)-5=(37-5)+28=60.
3. x+(y-z)=x+y-z: 51+(34-7)=51+32=19.
4. x-(y-z)=x-y+z: 66-(34-7)=(66-34)+7=39.
5. если x-y=z, то x=y+z: х-7=6, х=7+6, х=13.
6. если x-y=z, то y=x-z: 46-у=16, у=46-16, у=30.
7. если x-y=z, то (x+n)-y=z+n и (x-n)-y=z-n: 19-11=8, (19+6)-11=8+6, (19-1)+11=8-1.
8. если x-y=z, то x-(y+n)=z-n и x-(y-n)=z+n: 46-11=35, 46-(11+4)=35+4, 46-(11-9)=35-9.
9. если x-y=z, то (x+n)+(y-n)=z: 100-50=50, (100+10)+(50-10)=50.
10. если x-y=z, то (x+n)-(y+n)=z и (x-n)-(y-n)=z: 300-150=150, (300+25)-(150+25)=150, (300-25)-(150-25)=150.

Определение

Однозначное число — это число, состоящее из одной цифры.

Определение

Многозначное число — включающее две и более цифры.

Чтобы найти разницу между однозначными числами, стоит вычесть из первого слагаемого второе. В этом поможет таблица вычитания, которую заучивают наизусть.

Чтобы посчитать результат вычитания многозначных чисел, можно воспользоваться счетом «в столбик». Этот способ подразумевает, что вычитаемое записывают под уменьшаемым в соответствии с десятками, сотнями, тысячами и так далее. После этого, начиная с конца, то есть с десятков, производят вычисление.

Пример

653-132

Сначала находим разность единиц, то есть от 3 отнимаем 2. Получаем 1.

Затем вычисляем десятки, то есть от 5 отнимаем 3. Результат равен 2.

И, наконец, считаем сотни, то есть от 6 отнимаем 1 и получаем 5.

Ответ: 521.

Если одно и то же число вычитается из другого множество раз, то можно умножить данное значение на столько раз, сколько представлено в примере, и таким образом получить одно вычитаемое число.

Пример

440-10-10-10=440-(10*3)=440-30=410.

Что такое математическая разность

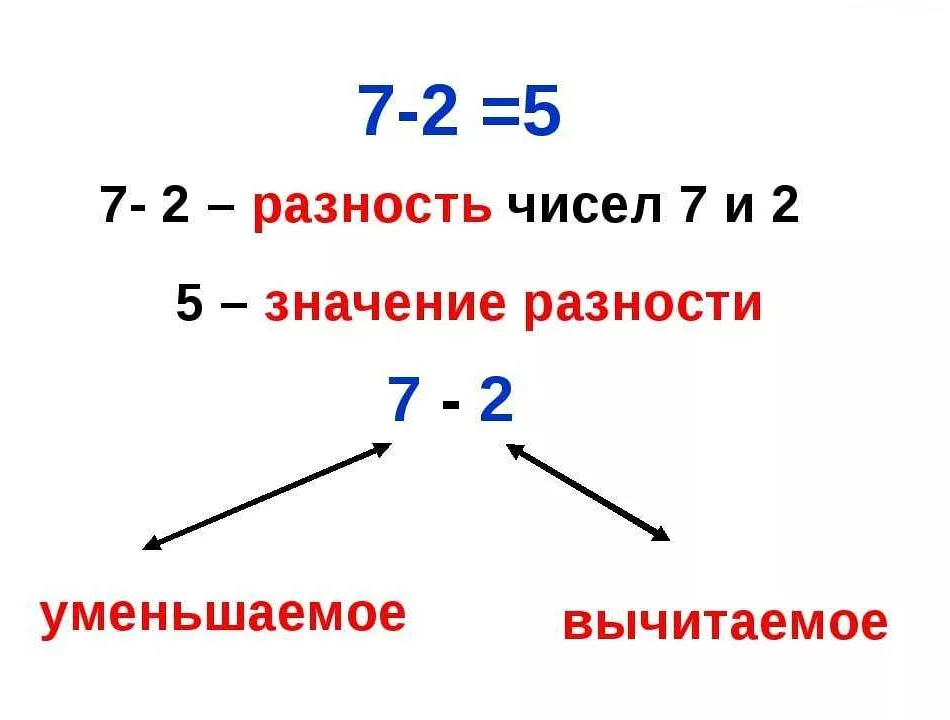
В математике под понятием «разность» понимается операция, которая предполагает вычитание одного числа из другого. Например, если у нас есть число 7, а мы вычитаем из него число 3, то получаем разность равную 4.

Математическую разность можно обозначить специальным знаком «-«, который применяется между вычитаемым и вычитателем. Если мы продолжим пример с числами 7 и 3, то математическая разность будет записана следующим образом: 7 — 3 = 4.

В зависимости от контекста, математическую разность можно использовать для решения различных задач. Например, при работе с графиками функций, математическая разность может быть использована для определения изменения значений функции в различных точках.

Стоит отметить, что математическая разность может применяться не только к целым числам, но и к числам с плавающей точкой (дробям). В таком случае, результат разности будет также являться числом с плавающей точкой.

Что такое рациональные числа

Рациональные числа — это все числа, которые можно представить в виде дроби m/n, где числитель m — это целое число, а знаменатель n — натуральное. Множество рациональных чисел обозначается латинской буквой Q.

Изображение: Skillbox Media

Например, число 0,5 можно представить как дробь 5/10 или ½, а значит, оно является рациональным. Математически это записывается как 0,5 ∈ Q.

Любое целое число тоже можно считать рациональным — ведь мы можем представить его в виде дроби. Например, число 5 можно записать как 5/1. Технически это будет неотличимо от деления 5 на 1, в результате которого получится та же самая пятёрка.

Изображение: Skillbox Media

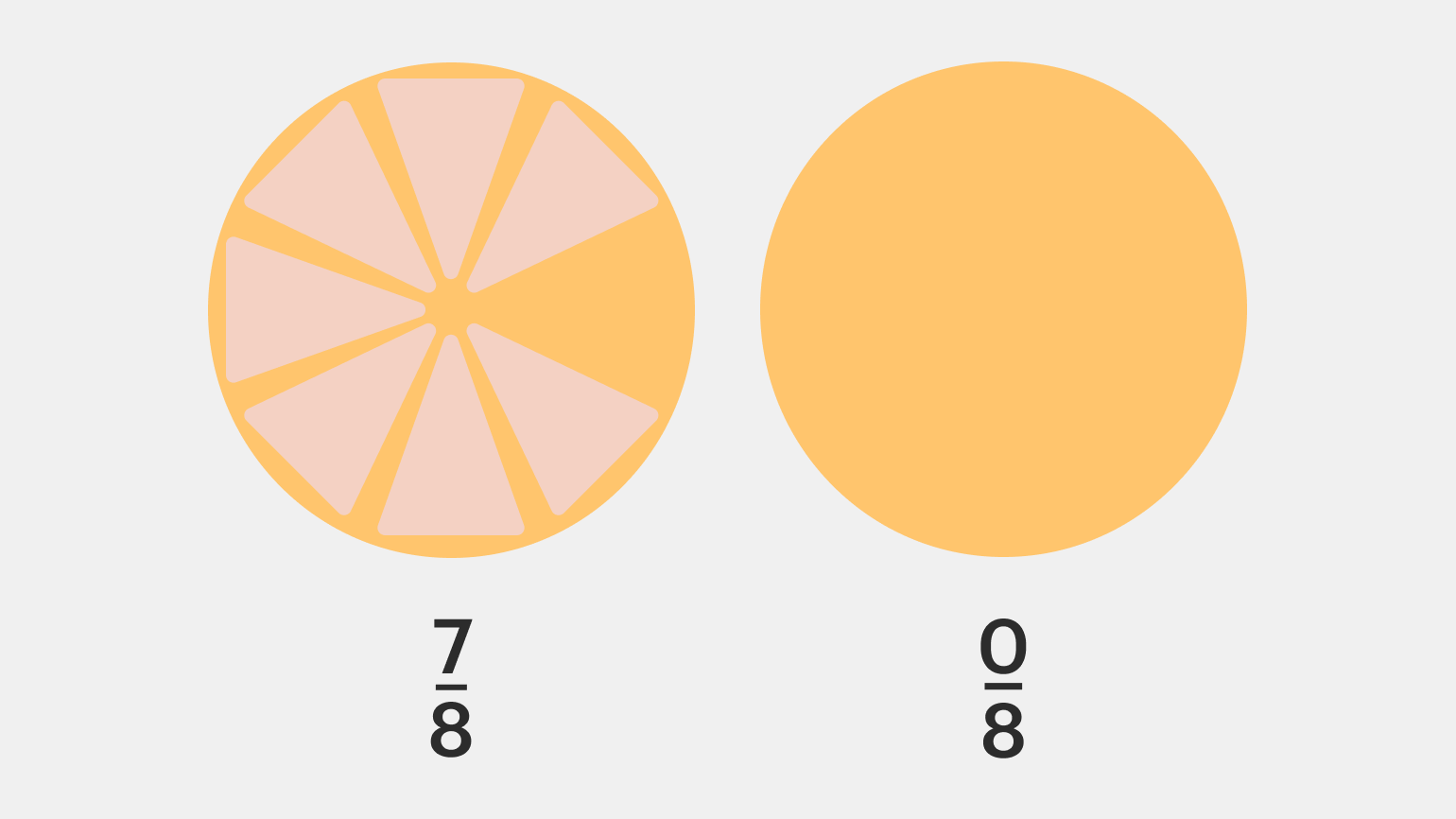
Ноль также относится к рациональным числам, потому что его мы тоже можем представить в виде дроби. Так как на ноль делить крайне не рекомендуется, знаменатель у ноля тоже не может быть меньше единицы. Проиллюстрировать это можно на примере пиццы: сначала у нас было 7 из 8 кусков, то есть дробь 7/8, а когда всё съели — стало 0/8:

Изображение: Skillbox Media

Бесконечные периодические дроби также относятся к рациональным числам. Например, если мы возьмём дробь 1/7 и попытаемся перевести её в обычный вид — то есть разделим 1 на 7, — то получим 0,14285714285714… Последовательность после запятой (период) 142857 будет повторяться до бесконечности, но при обратной операции мы снова получим дробь 1/7, а значит, это также относится к рациональному множеству.

Если после запятой у дроби нет никакой повторяющейся последовательности, то число уже называется иррациональным. Например √2 = 1,41421356237… Ещё один пример — знаменитое число π («пи») — 3,1415926535…

Примеры рациональных чисел:

Задачи с применением полуразности чисел

Понимание понятия полуразности чисел позволяет решать различные задачи, связанные с вычислениями и алгеброй. Рассмотрим несколько примеров задач, в которых полуразность чисел будет играть важную роль.

Пример 1:

Найдите полуразность чисел 15 и 8.

Для решения задачи используем формулу для вычисления полуразности: полуразность = (большее число — меньшее число) / 2.

Получаем полуразность = (15 — / 2 = 7 / 2 = 3.5

Ответ: полуразность чисел 15 и 8 равна 3.5.

Пример 2:

Вася купил четыре пирожка, а Петя — два. Найдите полуразность количества пирожков, купленных Васей и Петей.

Для решения задачи вычислим разность количества пирожков и найдем ее полуразность.

Разность = 4 — 2 = 2

Полуразность = 2 / 2 = 1

Ответ: полуразность количества пирожков, купленных Васей и Петей, равна 1.

Пример 3:

В коробке лежит 14 яблок, а на столе — 8. Найдите полуразность количества яблок в коробке и на столе.

Аналогично предыдущему примеру, вычислим разность количества яблок и найдем ее полуразность.

Разность = 14 — 8 = 6

Полуразность = 6 / 2 = 3

Ответ: полуразность количества яблок в коробке и на столе равна 3.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста. Расскажу, где снять крутую шлюху в Крыму. Вот сайт с проститутками: https://sexanketa-krym.com/ Очень крутые путаны.. Настоятельно советую присмотреться к данному ресурсу и заняться сексом, тем более это не дорого.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

• сумму — сложением слагаемых,
• произведение — умножением множителей,
• частное — делением делимого на делитель.

Вот такая интересная арифметика.

Свойства и особенности

Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций. Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат. Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.

В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.

Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?

В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.

Рациональные числа и их свойства.

Рациональное число — такое число, которое можно записать в виде p/q, где p — целое число, q — натуральное число. В частности, любое целое число является рациональным, поскольку его можно записать в виде p = p/1. Например, 0 = 0/1, 1=1/1.

Пусть a = p/q, b = p₁/q₁ — два рациональных числа. Тогда правило упорядочения этих чисел определяется так:

• если pq₁ = qp₁, то a = b;
• если pq₁ > qp₁, то a > b;
• если pq₁ < qp₁, то a < b;

а сумма и произведение чисел a и b определяется равенствами

$$a+b=\frac{pq_1+qp1}{qq_1}, \ ab=\frac{pp_1}{qq_1}\nonumber$$

Операции сложения и умножения рациональных чисел обладают свойствами:

• коммутативности:$$a+b=b+a, \ ab=ba\nonumber$$
• ассоциативности:$$(a+b)+c=a+(b+c), \ (ab)c=a(bc)\nonumber$$
• дистрибутивности:$$a(b+c)=ab+ac\nonumber$$
• для любого рационального числа a справедливы неравенства$$a+0=a, \ a\cdot1=a\nonumber$$

Операции вычитания и деления вводятся как обратные соответственно к операциям сложения и умножения:

• (для любых рациональных чисел a, b существует (и притом единственное) число x такое, что$$b+x=a\nonumber$$это число называют разностью чисел a и b и обозначают a — b).
• если b ≠ 0, то существует единственное число z такое, что$$bz=a\nonumber$$это число называют частным чисел a и b и обозначают a/b.

Отметим еще основные свойства неравенств для рациональных чисел:

• если a > b и b > c, то a > c (транзитивность);
• если a > b, то a + c > b +c при любом c;
• если a > b и c > d, то a + c > b + d;
• если a > b и c > 0, то ac > bc;
• если a > b и c < 0, то ac < bc.

В дальнейшем, мы будем использовать следующие обозначения:

• \(\mathbb{N}\) — множество натуральных чисел;
• \(\mathbb{Z}\) — множество целых чисел;
• \(\mathbb{Q}\) — множество рациональных чисел.

В множестве \(\mathbb{Q}\) можно выполнять не только четыре арифметических действия, но и решать уравнения и системы уравнений первой степени. Однако, даже простейшие квадратные уравнения вида x2=a, где \(a\in\mathbb{N}\), не всегда разрешимы в множестве \(\mathbb{Q}\). Так например, уравнение x2=3 не имеет решений в множестве рациональных чисел \(\mathbb{Q}\).

Докажем, что решение данного уравнения \(\sqrt{3}\) не является рациональным числом.

Давайте предположим противное, то есть что \(\sqrt{3}\) — рациональное число

Тогда по определению рациональных чисел можем записать его как несократимую (и это важно) дробь, то есть:
$$
\sqrt{3}=\frac{p}{q},\qquad p\in\mathbb{Z}, \ q\in\mathbb{N}\nonumber
$$
Возведем обе части в квадрат и преобразуем дробь. Получаем
$$
p^2=3q^2\nonumber
$$
Как видно из выражения, p2 делится на 3 без остатка

Если записать это «по-умному», то
$$
p^2 \ \equiv \ 0 \ (\operatorname{mod} \ 3)\nonumber
$$
Но это означает, что также и само p2 делится на три без остатка. В самом деле, любое натуральное число можно разложить на простые множители. Запишем p следующим образом:
$$
p=p_0^{x_0}\cdot p_1^{x_1}\cdot\ldots\cdot p_n^{x_n}\nonumber
$$
, где \(p_0,p_1,\ldots ,p_n\) — простые числа, а \(x_0,x_1,\ldots,x_n\) — целые числа).

Тогда p2 можно записать так:

$$
p^2=p_0^{2x_0}\cdot p_1^{2x_1}\cdot\ldots\cdot p_n^{2x_n}\nonumber
$$
Поскольку p2 делится на 3 целиком, то это значит, что в нашем разложении какое-то p_i = 3. А поскольку множество всех p_i (i лежит в пределах от 0 до n включительно) образует множество всех делителей исходного p, то 3 также является делителем p. То есть мы можем записать, что:
$$
p=3\cdot k,\qquad k\in\mathbb{N}\nonumber
$$
То есть, если вернемся к одному из первых утверждений и заменим наше p, то получим:
$$
9\cdot k^2=3\cdot q^2\quad\Leftrightarrow\quad q^2=3\cdot k^2\nonumber
$$
Повторяя вышеизложенные рассуждения, получим, что q так же делится на 3, как и p. Предположим, что:
$$
q=3\cdot m,\qquad m\in\mathbb{N}\nonumber
$$
Таким образом:
$$
\frac{p}{q}=\frac{3\cdot k}{3\cdot m}=\frac{k}{m},\nonumber
$$
что противоречит первоначальному утверждению, что p/q — несократимая дробь. Следовательно, \(\sqrt{3}\) не является рациональным. \(\bullet\)

Таким образом, уже проблема решения простых уравнений типа x2=a, x3=a, где \(a\in\mathbb{N}\), приводит к необходимости расширения множества рациональных чисел \(\mathbb{Q}\) путем добавления к этому множеству новых элементов, называемых иррациональными числами.

Примеры нахождения

Пример 1. Найти разницу двух величин.
Дано: 20 — уменьшаемое, 15 — вычитаемое.
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.

Пример 2. Найти уменьшаемое.
Дано: 48 — разность, 32 — вычитаемое значение.
Решение: 32 + 48 = 80
Ответ: 80.

Пример 3. Найти вычитаемое значение.
Дано: 7 — разность, 17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: 10.

И немного более сложных примеров, ведь в математике зачастую высчитывают разность с использованием не только двух, но и гораздо большего количества компонентов, в которых могут быть к тому же не только лишь целые числа, но и дробные, рациональные, иррациональные числа.

Пример 4. Найти разницу трех значений.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение, 12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2) 44 — 4 = 40.
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми);
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
2) 56 — 16 = 40.
Ответ: 40 — разница трех значений.

Пример 5. Найти разницу величин 7 и 18.
Дано: 7 — уменьшаемое значение, 18 — вычитаемое.
Вроде все просто, но ведь вычитаемое у нас больше уменьшаемого, как быть в таком случае? В таком случае действует следующее правило: если вычитаемое больше уменьшаемого, то разность окажется отрицательной или другими словами, она будет числом со знаком минус.
Решение: 7 — 18 = —11
Ответ: —11 — отрицательное число со знаком минус.

Схожі записи:

Под знаком интеграла – математическая пьеса

Рассказ о необыкновенных вычислениях

Электронный скальд: о связи математики и поэзии

Блестящая непопулярность математики

Совершенные числа

Что такое разность потенциалов

Понятие разности потенциалов используется физиками. Получить разность потенциалов можно, подключив вольтметр к двум точкам цепи, где напряжение первой условно равно U1, а второй — U2. В таком случае вольтметр покажет результат в виде напряжения U1-U2, что и называется разностью потенциалов. Любой гальванический элемент вырабатывает напряжение, которое определяет разность электрохимических потенциалов, составляющих электроды элемента веществ.

До того, как были изобретены стабилизаторы напряжения, осуществить калибровку вольтметров позволяли элементы Вестона. Подобранные в них реагирующие составляющие обеспечивали высокий уровень стабильности разности потенциалов. Также существует понятие разности давлений, использующееся в гидравлическом и пневматическом оружии. Такая разность представляет собой аналог разности электротехнических потенциалов.

Что такое полуразность

В общем случае, полуразность между двумя элементами задается при помощи определенной функции. Эта функция принимает на вход два элемента и возвращает значение, указывающее на связь или отношение между ними. Например, полуразность может быть определена для числовых множеств, где функция проверяет, является ли одно число больше или меньше другого.

Применение полуразности в разных областях знаний

Понятие полуразности находит применение в различных областях знаний, таких как математика, логика, информатика и другие. В математике полуразность может использоваться для определения отношений частичного порядка или системы классификации элементов внутри множества.

В целом, полуразность является важным понятием, позволяющим анализировать и определять связи между элементами различных множеств в более глубокой и детализированной форме. Ее использование дает возможность более точно описывать и понимать взаимодействия в рамках разных дисциплин и областей знаний.

Как найти разность чисел

В общем виде вычитание можно записать так: a — b = r.Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел , возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.

Сравнение вещественных чисел.

Сравнение неотрицательных чисел.

Два неотрицательных вещественных числа

$$\alpha=a_0,a_1a_2…a_n…\qquad\beta=b_0,b_1b_2…b_n…\nonumber$$

называют равными и пишут α = β при k = 0,1,2,…, то есть

$$\left\{\alpha=\beta\right\}\Leftrightarrow\left\{a_k=b_k, \ k=0,1,2,…\right\}.\nonumber$$

Например,

$$\left\{\alpha=0\right\}\Leftrightarrow\left\{a_k=0, \ k=0,1,2,…\right\}.\nonumber$$

Дадим определение α < β и α > β. Говорят, что число α меньше числа β и пишут α < β, если либо a < b, либо a = b и существует такой номер n, что a₁ = b₁, a₂ = b₂,…, a_n-1 = b_n-1, но a_n < b_n, то есть

$$\left\{\alpha < \beta\right\} \ \Leftrightarrow \ \left\{a_0 < b_0\right\}\vee\left\{\exists n\in\mathbb{N}: \ a_k=b_k, \ k=\overline{0, \ n-1}; \ a_n < b_n\right\}.\nonumber$$

Запись \(k=\overline{0, \ n-1}\) означает, что равенство a_k = b_k выполняется при значениях k от 0 до n-1 включительно, так что n — наименьший номер, для которого это неравенство не выполняется и имеет место неравенство a_n < b_n. Аналогично,

$$\left\{\alpha > \beta\right\} \ \Leftrightarrow \ \left\{a_0 > b_0\right\}\vee\left\{\exists n\in\mathbb{N}: \ a_k=b_k, \ k=\overline{0, \ n-1}; \ a_n > b_n\right\}.\nonumber$$

Из определения равенства α = β и неравенств α < β и α > β следует, что для любых неотрицательных вещественных чисел α и β выполняется одно из трех условий: α = β, α < β, α > β.

Отметим, что для любого неотрицательного вещественного числа α справедливо неравенство α ≥ 0.

Сравнение произвольных вещественных чисел.

Назовем модулем вещественного числа α вещественное число, обозначаемое символом |α|, представимое той же бесконечной дробью, что и α, но взятое со знаком +. Таким образом, если

$$\alpha=\pm a_0,a_1a_2…a_n…,\qquad то\qquad\left|\alpha\right|=a_0,a_1a_2…a_n…,\nonumber$$

откуда следует, что |α| — неотрицательное вещественное число при любом α.

Введем правило сравнения двух вещественных чисел α и β для случая, когда хотя бы одно из этих чисел отрицательно.

Если α — неотрицательное, β — отрицательное число, то считают, что α > β.

Если оба числа α и β отрицательны, то будем считать, что:

1. α = β, если |α| = |β|;
2. α < β, если |α| > |β|.

Замечание 1.

Легко убедиться в том, что сформулированное правило сравнения вещественных чисел в применении к рациональным числам, записанным в виде бесконечных десятичных дробей, приводит к тому же результату, что и правило сравнения рациональных чисел (), представленных в виде отношения целых чисел.

Замечание 2.

Если \(\underline{\alpha}_n\), \(\underline{\beta}_n\) — n-е приближение с недостатком, а \({\overline\alpha}_n\), \({\overline\beta}_n\) — n-е приближение с избытком чисел α и β соответственно, то из правила сравнения вещественных чисел следует, что:

1. \(\underline{\alpha}_n\leq\alpha\leq{\overline\alpha}_n, \ \underline{\beta}_n\leq\beta\leqslant{\overline\beta}_n\) для любого n ∈ \(\mathbb{N}\);
2. \(\alpha < \beta\Rightarrow\exists n: \ {\overline\alpha}_n < \underline{\beta_n}\).

Транзитивность правил сравнения.

Докажем, что если α < β и β < γ, то α < γ. Ограничимся доказательством случая, когда сравниваются неотрицательные числа. Пусть

$$\begin{array}{l}\alpha=a_0,a_1a_2…a_n…\\\beta=b_0,b_1b_2…b_n…\\\gamma=c_0,c_1c_2…c_n…\end{array}\nonumber$$

Пусть p и m — наименьшие номера, для которых нарушаются соответственно равенства a_k = b_k и b_k = c_k (k = 0, 1, 2,…), и пусть, например p ≤ m. тогда p — наименьший номер, при котором нарушается равенство а_k = c_k и имеет место неравенство a_p < c_p. По правилу сравнения вещественных чисел отсюда следует, что α < γ.

Проверка результата вычитания.

Как проверить правильно ли вы нашли разность двух целых чисел?
Ответ прост он заключается в самом определении разности двух целых чисел. Нужно разность сложить с вычитаемым получим уменьшаемое
. Словесная формула будет выглядеть так:

Разность+Вычитаемое=Уменьшаемое

Пример:

19-5=14

19 – это у нас уменьшаемое;
5 – вычитаемое;
14 – разность.

Выполним проверку:
К разности прибавим уменьшаемое, если правильно выполнили вычитание, то получим уменьшаемое.

Еще пример:

Выполните проверку вычитания 12-23=-11

12 – уменьшаемое;
23 – вычитаемое;
-11 – разность.

Выполним проверку вычитания:
Разность+Вычитаемое=Уменьшаемое