Убывание – что означает? Определение, значение, примеры употребления
Ищешь, что значит слово убывание? Пытаешься разобраться, что такое убывание? Вот ответ на твой вопрос:
Значение слова «убывание» в словарях русского языка
Убывание это:
1.процесс действия по гл. убывать I
2.Результат такого действия; уменьшение, снижение, сокращение. II ср. разг.
1.процесс действия по гл. убывать II
2.Результат такого действия; уход, отбытие.
Убывание
ср. Процесс действия по знач. глаг.: убывать.
Убывание
убывание ср. Процесс действия по знач. глаг.: убывать.
Убывание
убывание, -я
Убывание
; уменьшаться, снижаться в количестве, размере, степени результат такого действия; уменьшение, снижение, сокращение ; уходить, удаляться, исчезать результат такого действия; уход, отбытие
Где и как употребляется слово «убывание»?
Кроме значения слова «убывание» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «убывание».
Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «убывание» в тексте и устной речи.
Примеры употребления слова «убывание»
Важно соблюдать порядок убывания цен – от более дорогого к более дешёвому. Сценарии будем рассматривать по мере убывания вероятности их реализации в ближайшие 20 лет. Сценарии будем рассматривать по мере убывания вероятности их реализации в ближайшие 20 лет
Сценарии будем рассматривать по мере убывания вероятности их реализации в ближайшие 20 лет.
Традиционно статьи активов располагаются в балансе по степени убывания ликвидности сверху вниз, от наиболее ликвидных к наименее ликвидным.
Сортировка строк по длине в Python
main.py
Данный код выполняет сортировку списка на основе длины строк в нем с использованием функции и метода с ключом сортировки и аргументом для обратной сортировки.
Пояснение к коду:
— создание списка с данными строками.
— вызов метода на списке с ключом сортировки , что указывает на сортировку списка на основе длины строк в порядке возрастания. Результат сортировки сохраняется в самом списке .
— вывод отсортированного списка strings на экран. Результат будет , так как строки отсортированы в порядке возрастания длины.
— вызов функции с аргументом , ключом сортировки и аргументом , что указывает на сортировку списка на основе длины строк в порядке убывания. Результат сортировки сохраняется в переменной .
— вывод отсортированного списка на экран. Результат будет , так как строки отсортированы в порядке убывания длины с использованием функции .
Значение словосочетания «по убыванию»

по убыванию
1. так, что каждый следующий меньше по отношению к предыдущему ◆ Элементы любого списка можно упорядочить по алфавиту, а также рассортировать по возрастанию или по убыванию значений.
Делаем Карту слов лучше вместе
Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова артдивизион (существительное):
Предложения со словосочетанием «по убыванию»
И так далее по убыванию расположены все оставшиеся постоянные клиенты.
Цитаты из русской классики со словосочетанием «по убыванию»
— Милый, милый! — шептала она в исступлении, закрывая глаза. — Только один раз. Разве та, другая, умеет любить? А я-то тосковала по нем, я-то убивалась!
Понятия, связанные со словосочетанием «по убыванию»
Поря́дковые стати́стики в математической статистике — это упорядоченная по неубыванию выборка одинаково распределённых независимых случайных величин и её элементы, занимающие строго определенное место в ранжированной совокупности.
Предложения со словосочетанием «по убыванию»
И так далее по убыванию расположены все оставшиеся постоянные клиенты.
Для принятия решения в этом случае упрощённо, все имеющиеся проекты сортируются по убыванию индекса прибыльности и принимаются сверху вниз до момента, когда закончится лимит доступных инвестиций.
После того как таблица будет построена, строчки необходимо отсортировать по убыванию количества символов.
Источник
Как определить порядок убывания чисел
Для определения порядка убывания чисел, нужно сравнить их значения. Числа считаются убывающими, если каждое последующее число меньше предыдущего.
Существует несколько способов определить порядок убывания чисел:
- Сравнить числа попарно. Если каждое следующее число меньше предыдущего, то числа идут в порядке убывания.
- Упорядочить числа по убыванию. Если все числа стоят в правильном порядке, значит числа упорядочены в порядке убывания.
- Использовать знаки сравнения. Если все знаки сравнения между числами написаны в правильном порядке (например, >, >, >), то числа идут в порядке убывания.
Например, для чисел 5, 3, 1 можно сравнить их попарно: 5 > 3, 3 > 1. Значит, числа идут в порядке убывания.
Теперь ты знаешь, как определить порядок убывания чисел
Это важное понятие поможет тебе лучше понять математику и решать различные задачи
Двойные и тройные неравенства
Математике известно, что 5 < 12, а 12 < 35. Два данных неравенства возможно показать в форме одного двойного неравенства. Данная запись обладает следующим видом: 5 < 12 < 35. Видно, что в процессе записи двойного неравенства получится три неравенства, которые можно записать как 5 < 12, 12 < 35 и 5 < 35.
В форме двойного неравенства можно сделать запись в процессе сравнения трех чисел. Когда нужно совершить сравнение 76, 512 и 10, у нас может получиться целых три неравенства 76 < 512, 76 > 10, 512 > 10. Данные неравенства также можно записать как одно, но двойное: 10 < 76 < 512.
Точно так же можно совершить и тройные, и четверные, и другие неравенства. Так, известно, что 5 < 16, 16 < 305, 305 < 1001, 1001 < 3214. Тогда можно показать запись в следующем виде: 5 < 16 < 305 < 1001 < 3214. Нужно проявлять крайнюю внимательность тогда, когда составляются двойные неравенства, потому что можно составить их неверно, что повлечет за собой неверное решение задачи.
Условия порядка убывания
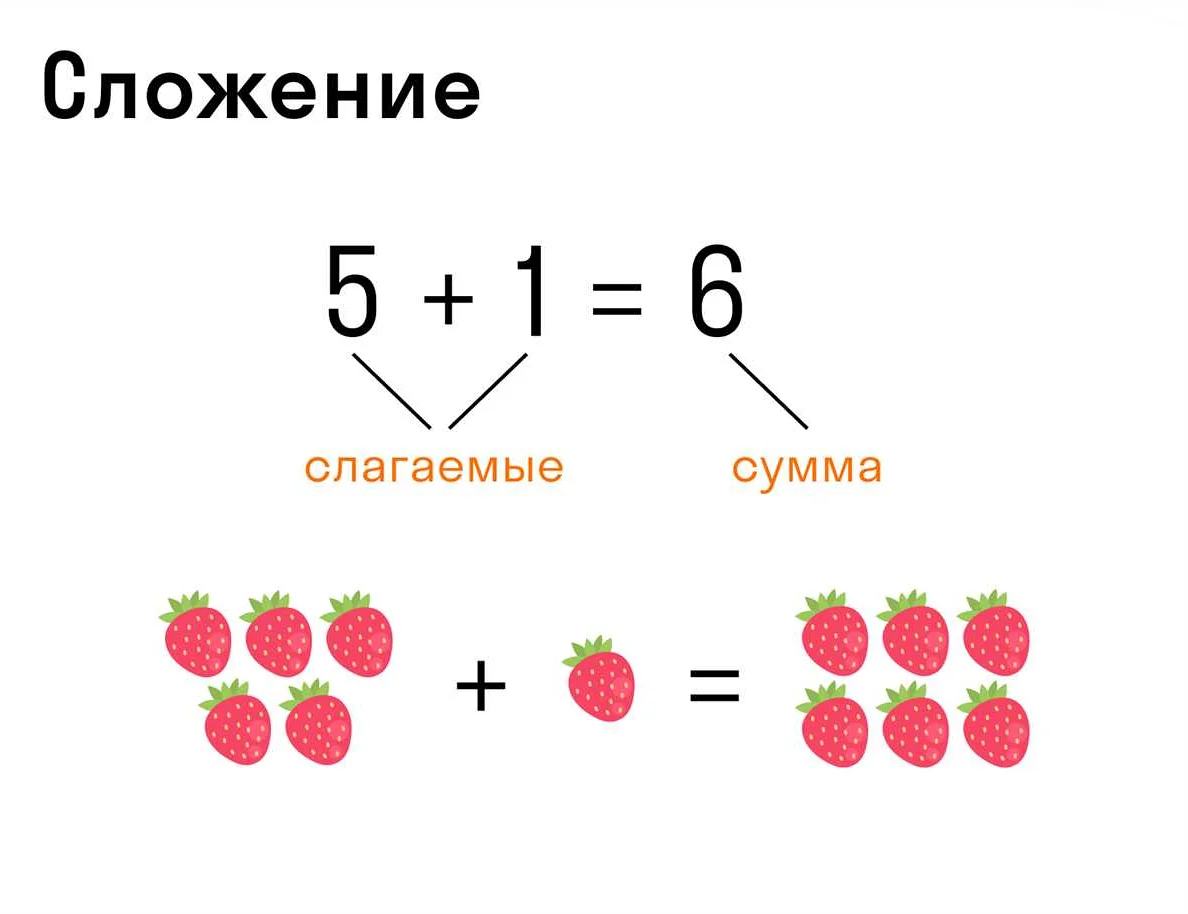
Порядок убывания в математике определяет, в каком порядке значения функции уменьшаются при изменении независимой переменной. Чтобы определить порядок убывания, необходимо учитывать несколько условий.
1. Функция должна быть определена на заданном интервале. Если функция не определена на данном интервале, то невозможно сказать, убывает она или возрастает.
2. На данном интервале производная функции должна быть отрицательной. Если производная положительна или равна нулю, то функция возрастает или остается постоянной.
3. Функция должна быть непрерывной на заданном интервале. Если функция имеет разрывы или точки разрыва, то она может менять свой порядок убывания.
4. Определенная функция должна быть строго монотонно убывающей на заданном интервале. Если функция имеет области с постоянным значением или скачки, то порядок убывания будет нарушен.
Условия порядка убывания позволяют определить, как меняется функция при изменении независимой переменной
Это важное понятие в математике, которое позволяет анализировать и предсказывать поведение функций на заданных интервалах
Польза изучения убывания чисел

Изучение убывания чисел позволяет:
| 1. | Анализировать статистические данные |
| 2. | Понимать тренды и паттерны |
| 3. | Проводить прогнозирование и моделирование |
| 4. | Принимать обоснованные решения на основе информации |
| 5. | Разрабатывать стратегии в различных областях |
Например, в финансовой аналитике знание убывания чисел позволяет анализировать изменения в ценах акций и предсказывать их будущую динамику. В научных исследованиях изучение убывания чисел помогает анализировать данные и определять закономерности в результате эксперимента.
В общем, понимание и умение работать с убывающими числами позволяет нам лучше понимать окружающий мир и принимать обоснованные решения на основе имеющихся данных.
Рациональные числа на координатной прямой
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:
На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.
Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей
Попробуем понять, почему дробь вдруг расположилась между нулём и единицей.
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину
Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.
Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и равна 0,5
А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь
Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2
Значение дроби равно 1,5
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:
Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2
Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:
Пример 3. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться очень близко к нулю
Значение дроби равно 0,02
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3
Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3
это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.
Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь
Значение дроби равно 2,5
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 2,5
Дискуссии[]
Аксиома
Чтобы определить натуральное число с помощью теории множеств, нам нужно зафиксировать, в соответствии с какими аксиомами мы его определяем. Проблема в определении числа Райо заключается в том, что мы не разъяснили аксиомы. В математике мы традиционно опускаем объявление аксиом, в которых мы работаем, до тех пор, пока мы не работаем в ТМЦФ. По традиции несколько гугологов считают, что число Райо определено в ТМЦФ или не имеет отношения к аксиомам, но это неверно.
По крайней мере, поскольку ТМЦФ не способна формализовать предикат истинности во вселенной фон Неймана, число Райо плохо определено в ТМЦФ, если мы не интерпретируем определение числа Райо в терминах доказуемости. Даже если мы интерпретируем определение таким образом, результирующее большое число не будет значительно больше, чем, например, Σ(10100) где Σ — функция занятого бобра, поскольку доказуемость в рекурсивно перечислимой теории с ограничением длины разрешимо с помощью машины Тьюринга. Чтобы значительно выйти за рамки функции занятого бобра, мы должны отказаться от доказуемости и говорить об истинности в конкретной модели, существование которой не доказуемо в рамках ТМЦФ до тех пор, пока она непротиворечива.
С другой стороны, FOOT — это всего лишь формальный язык, который по определению не имеет отношения к аксиоме, но это не означает, что число Райо не имеет отношения к аксиомам. Неуместность FOOT и аксиом или связь между функцией занятого бобра и основанной на доказательствах интерпретацией определения числа Райо могут быть основными причинами неправильного понимания того, что число Райо не имеет отношения к аксиомам.
Поскольку Райо писал, что он использует теорию множеств второго порядка для того, чтобы формализовать словарь примитивной семантики в исходном описании, число Райо определяется в соответствии с определёнными аксиомами теории множеств второго порядка, которые не уточняются
Важно прояснить аксиомы в невычислимой гугологии, потому что невычислимые большие числа можно сравнивать друг с другом только тогда, когда они разделяют аксиомы, используемые в их определениях. К счастью, существует множество вариантов аксиом теории множеств второго порядка, которые позволяют нам определить число Райо
В качестве вывода: «Число Райо хорошо определено для гугологов, которые не заботятся об уточнении аксиом, и плохо определено для гугологов, которые заботятся об уточнении аксиом».
В 2020 году Райо добавил следующее новое описание того, как обращаться с его числом:
- Примечание: Философы иногда придерживаются реалистической интерпретации теории множеств. Согласно этой интерпретации, теоретико-множественные выражения имеют «стандартные» значения, которые определяют определённое значение истинности для каждого предложения языка, независимо от того, возможно ли в принципе узнать, каковы эти значения истинности. (Смотрите, например, эту статью Ванна Макги.) Во время конкурса мы с Адамом считали само собой разумеющимся, что язык теории множеств (второго порядка) интерпретировался стандартно, что гарантирует, что итоговая заявка соответствует определённому числу. Если бы вместо этого язык интерпретировался на основе системы аксиом, окончательная запись была бы недействительной. Это связано с тем, что каждая (непротиворечивая) аксиоматизация языка имеет неизоморфные модели, и нет никакой гарантии, что конечная запись будет соответствовать одному и тому числу относительно разных моделей.
Это означает, что Райо рассматривает философскую «интерпретацию» теоретико-множественных формул по отношению к «истине» в реальном мире, которая неформализуема в математике, и не предполагает конкретного выбора аксиом. Это одно из разумных направлений гугологии за пределами математики. С другой стороны, проблема в последнем предложении выглядит как оправдание того, почему они принимают неформализуемую «истину» как должное, но это не имеет смысла, потому что зависимость значения данного числа от модели не имеет отношения к «недействительности». В математике существует много чётко определённых понятий, которые не являются абсолютными, т.е. зависят от модели, например, уникальное натуральное число n{\displaystyle n}, удовлетворяющее (CH→n=)∧(¬CH→n=1){\displaystyle (\text{CH} \to n=0) \land (\neg\text{CH} \to n=1)}. В гугологии есть много больших чисел, которые зависят от модели, например, значения функции занятого бобра и особенно S(1919){\displaystyle S(1919)}, где S{\displaystyle S} обозначает функцию максимального сдвига. В дуэли больших чисел нет правила, запрещающего число, которое зависит от модели, и действительно, оно даже позволяет пропускать, чтобы исправить аксиомы.
Вопрос-ответ:
Что такое порядок убывания в математике?
Порядок убывания в математике — это способ описания поведения функции при стремлении аргумента к бесконечности. Функция называется убывающей, если ее значения уменьшаются при увеличении аргумента.
Как определить порядок убывания функции?
Для определения порядка убывания функции нужно рассмотреть ее производную. Если производная функции всегда отрицательна на заданном интервале, то функция является убывающей.
Дайте пример убывающей функции.
Примером убывающей функции может быть f(x) = -2x + 5. При увеличении значения x, значение функции f(x) будет уменьшаться.
Есть ли правила для определения порядка убывания?
Да, существуют правила для определения порядка убывания функций. Например, если у функции есть положительная первая производная, то она будет убывать. Также, если вторая производная функции отрицательна, то она также будет убывать.
Может ли функция быть одновременно возрастающей и убывающей?
Нет, функция не может быть одновременно возрастающей и убывающей на одном и том же интервале. Она может либо возрастать, либо убывать, или быть постоянной.
Отличие от обычной разницы
Понимание понятия «на порядок больше или меньше» имеет свои особенности. Оно отличается от обычного понятия разницы.
Разница между двумя числами — это просто разность между ними. Например, разница между числами 7 и 3 равна 4.
Однако, когда мы говорим о числах, которые отличаются «на порядок», мы имеем в виду разницу в значении экспоненты, а не само число. Когда число A на порядок больше числа B, это означает, что A в «научной нотации» записывается с большим показателем степени, чем B.
Например, если число A равно 1.2×106, а число B равно 1.2×105, то число A на порядок больше числа B. Это можно увидеть, сравнивая показатели степени 6 и 5.
Обратите внимание, что само значение перед экспонентой (в данном случае, 1.2) не имеет значения при определении, насколько одно число больше или меньше другого на порядок. Для лучшего понимания, вот наглядная таблица, где числа сравниваются по их показателям степени:. Для лучшего понимания, вот наглядная таблица, где числа сравниваются по их показателям степени:
Для лучшего понимания, вот наглядная таблица, где числа сравниваются по их показателям степени:
| Число | Научная нотация | Показатель степени |
|---|---|---|
| 1000 | 1.0×103 | 3 |
| 100 | 1.0×102 | 2 |
| 10 | 1.0×101 | 1 |
| 1 | 1.0×10 | |
| 0.1 | 1.0×10-1 | -1 |
| 0.01 | 1.0×10-2 | -2 |
Из таблицы видно, что чем больше показатель степени, тем больше число. Например, 1000 на порядок больше, чем 100, так как их показатели степени различаются на 1.
Теперь, когда вы знаете, что означает «на порядок больше или меньше», вы сможете легче ориентироваться в числовых значениях и их сравнении по экспонентам.
Упражнения
1. Дан линейный массив (вектор) из целых чисел. Написать программу сортировки массива. Данные сгенерировать случайным образом.
-
- Так, чтобы все кратные трем стояли в начале массива, а не кратные в конце.
- В порядке возрастания суммы цифр числа.
- В порядке убывания количества делителей числа.
2. Дан линейный массив (вектор) из слов. Написать программу сортировки массива. Данные читать из файла.
-
- По количеству букв в слове, в порядке возрастания.
- По количеству согласных букв в слове, в порядке убывания.
- По количеству различных букв в слове, в порядке возрастания.
3. Дан линейный массив (вектор) из структур. Написать программу сортировки массива. Данные читать из файла. Можно использовать файлы, созданные для упражнения 6 после § 17.
1. В файле хранятся: название страны, столица, площадь (тыс. км2) и количество населения (млн чел.).
БеларусьМинск2089.41
РоссияМосква17075143.3
СШАВашингтон9373310.2
КанадаОттава998534.2
ФранцияПариж54765.4
И т.д.
Отсортировать данные в порядке возрастания площади.
2. В файле хранятся: название производителя стиральной машины, ее модель, мощность и максимальная загрузка белья (кг).
SamsungWW65K52E69S24006.5
BoschWLT24440OE23007
HaierHW70-BP12758S19007
LGF12M7NDS017006
И т.д.
Отсортировать данные в алфавитном порядке по названию производителя.
3. В файле хранятся: название озера, область в которой расположено, его объем (млн м3), площадь (км2), максимальная глубина (м) и прозрачность(м).
НарочьМинская71079.624.87.4
СнудыВитебская1072216.56.6
РичиВитебская131.512.951.95.5
СвитязьГродненская7.7625.2155.2
И т.д.
Отсортировать данные в порядке убывания прозрачности.
4*. Провести исследование методов сортировок (выбором, обменом и вставками). Подготовить отчет в электронных таблицах (можно использовать совместный доступ к таблице). Программы для каждой сортировки скомпилировать в режиме release. Запускать откомпилированные программы из операционной системы, используя файловый менеджер.
Для измерения времени можно использовать int t1 = clock(); из библиотеки ctime, выдает время в миллисекундах. Время замерять до начала работы алгоритма и после окончания работы алгоритма (разница — время работы алгоритма).
Для выполнения работы руководствоваться следующим планом (для каждого алгоритма):
-
- Сгенерировать текстовый файл из 20 000 целых чисел (диапазон чисел: –10000..10000).
- Измерить и записать время работы программ для полученного файла.
- Сгенерировать текстовый файл из 20 000 целых чисел (диапазон чисел: –100..100).
- Измерить и записать время работы программ.
- Увеличить количество элементов в пунктах 1 и 3 в два раза (до 40 000). Как изменить время выполнения программы?
- Пункты 1—5 выполнить 10 раз.
- Отсортировать в обратном порядке уже отсортированный массив для:
7.1. 20000 целых чисел (диапазон чисел –10000..10000). 7.2. 20000 целых чисел (диапазон чисел –100..100); 7.3. 40000 целых чисел (диапазон чисел –10000..10000; 7.4. 40000 целых чисел (диапазон чисел –100..100).
8. Найти среднее значение времени по всем видам сортировок (от суммы отнять минимальное, максимальное и разделить на 8). 9. Определить минимальное количество элементов, при которых каждая программа будет работать больше 30 секунд.
5*. Определить время работы алгоритма быстрой сортировки для тех же файлов, которые использовались в упражнении 4. Сделать выводы.
Разбор понятия в порядке убывания

Для определения порядка убывания необходимо сравнивать значения чисел между собой. Если значение следующего числа меньше значения предыдущего, то числа расположены в порядке убывания. Например, последовательность чисел: 5, 4, 3, 2, 1 — является последовательностью в порядке убывания. Также можно использовать знак «≥» для определения порядка — если каждое следующее число больше или равно предыдущему, то числа расположены в порядке убывания или равные.
Важно отметить, что порядок убывания может быть определен только для упорядоченных множеств, где имеется определенная структура или правило сравнения элементов. В математике, таким множеством является множество действительных чисел или любое другое множество, где определено отношение порядка
Итак, понятие в порядке убывания в математике играет важную роль при анализе последовательностей чисел и функций. Оно позволяет определить закономерности и свойства числовых последовательностей и функций, и использовать их для решения различных математических задач.
Выводы о понятии чисел больше и меньше 5
Понятие чисел “больше” и “меньше” 5 является основополагающим в математике. Число считается больше 5, если оно находится правее 5 на числовой прямой, а считается меньше 5, если оно находится левее прямой. Данное разделение чисел на больше и меньше позволяет нам проводить сравнения, операции и анализировать числовые данные.
Чтобы определить, является ли число больше или меньше 5, мы сравниваем его с числом 5. Если число больше 5, то оно располагается правее числа 5 на числовой прямой. Например, число 7 больше 5, так как оно находится правее числа 5. Если число меньше 5, то оно располагается левее числа 5 на числовой прямой. Например, число 3 меньше 5, так как оно находится левее числа 5.
Числа больше и меньше 5 имеют свои особенности при совершении арифметических операций. При сложении или умножении числа на 5, результат всегда будет больше и не может быть меньше 5. Например, 5 + 3 = 8, что больше 5. Однако, при вычитании, результат может быть как больше, так и меньше 5. Например, 5 – 3 = 2, что меньше 5. Это связано с установленными правилами математики для проведения арифметических операций.
В итоге, понятие чисел больше и меньше 5 является базовым для понимания сравнения и анализа числовых данных. Оно позволяет определять взаимное расположение чисел на числовой прямой и проводить различные математические операции. Знание этих понятий не только помогает в повседневной жизни, но также является основой для изучения более сложных математических концепций и теорий.





![Беседа 5. математические понятия и их определения [1985 фридман л.н. - учитесь учиться математики]](http://podomu.info/wp-content/uploads/8/0/5/80500f03224f3bdc07c14e8c9a7bfc57.jpeg)






















