Значение выражения «ни прибавить ни отнять»
Выражение «ни прибавить ни отнять» обозначает точную точку зрения или факт, который является неоспоримым. Существует фраза «точно как дважды два четыре», которая отрицательно выражает эту идею, говоря, что это ничего более, чем ожидаемый и предсказуемый результат. Однако, выражение «ни прибавить ни отнять» используется для выражения идеи, что нет никакой возможности изменить или дополнить существующее утверждение.
Данный термин используется в различных областях, в том числе в науке, познании законов природы, математике, анализе данных и многих других областях. В этих областях «ни прибавить и ни отнять» используется для обозначения закона или теории, которые были установлены и проверены, и в результате нельзя изменить это утверждение, чтобы добавить новые факты, которые могут быть известны в будущем.
Например, в математике выражение «ни прибавить ни отнять» может быть использовано для описания формулы или теоремы, которые уже были доказаны и не требуют никаких изменений или уточнений. Примером такой формулы может быть уравнение e = mc² Альберта Эйнштейна, так как после многих проверок и экспериментов невозможно изменить эту формулу, без нарушения отношения массы и энергии.
Выводы:
- Выражение говорит о неоспоримом факте.
- Термин используется в науке, математике, познании законов природы и других областях.
- Несомненное утверждение нельзя изменить, дополнить или скорректировать.
Формулы логики высказываний
Понятие логической формы сложного высказывания уточняется с помощью понятия формулы
логики высказываний.
В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания.
Вообще-то они называются формулами логики высказываний.
Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы
Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные
значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее
называть их элементарными формулами или атомами.
Для построения формул логики высказываний кроме указанных выше букв используются знаки
логических операций
~, ∧, ∨, →, ,
а также символы, обеспечивающие возможность однозначного прочтения формул — левая и
правая скобки.
Понятие формулы логики высказываний определим следуюшим
образом:
1) элементарные формулы (атомы) являются формулами логики высказываний;
2) если и —
формулы логики высказываний, то , ,
, ,
тоже являются формулами логики
высказываний;
3) только те выражения являются формулами логики высказываний, для которых это
следует из 1) и 2).
Определение формулы логики высказываний содержит перечисление правил образования
этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется
из атомов в результате последовательного применения правила 2).
Пример 6. Пусть — одиночное
высказывание (атом) «Все рациональные числа являются действительными», —
«Некоторые действительные числа — рациональные числа», —
«некоторые рациональные числа являются действительными». Переведите в форму словесных высказываний
следующие формулы логики высказываний:
1) ;
2) ;
3) ;
4) ;
5) ;
6) .
Решение.
1) «нет действительных чисел, которые являются рациональными»;
2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;
3) «если все рациональные числа являются действительными, то некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными»;
4) «все действительные числа — рациональные числа и некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными числами»;
5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;
6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».
Пример 7. Составьте таблицу истинности для формулы
логики высказываний , которую в
таблице можно обозначить .
Решение. Составление таблицы истинности начинаем с записи значений («истина» или «ложь»)
для одиночных высказываний (атомов) , и
. Все возможные значения записываются в восемь строк таблицы. Далее,
определяя значения операции импликации, и продвигаясь вправо по таблице, помним, что значение равно «лжи» тогда, когда из «истины» следует «ложь».
| И | И | И | И | И | И | И | И |
| И | И | Л | И | И | И | Л | И |
| И | Л | И | И | Л | Л | Л | Л |
| И | Л | Л | И | Л | Л | И | И |
| Л | И | И | Л | И | Л | И | И |
| Л | И | Л | Л | И | Л | И | Л |
| Л | Л | И | И | И | И | И | И |
| Л | Л | Л | И | И | И | Л | И |
Заметим, что никакой атом не имеет вида
, ,
, ,
. Такой вид имеют сложные формулы.
Число скобок в формулах логики высказываний можно уменьшить, если принять, что
1) в сложной формуле будем опускать внешнюю пару скобок;
2) упорядочим знаки логических операций «по старшинству»:
, →, ∨, ∧, ~ .
В этом списке знак имеет самую большую область действия, а знак ~ — самую
маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым
применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать
во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при
восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака ~ (при
этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.
Пример 8. Восстановите скобки в формуле логики высказываний
.
Решение. Скобки восстанавливаются пошагово следующим образом:
Не всякая формула логики высказываний может быть записана без скобок. Например, в
формулах и
дальнейшее исключение скобок
невозможно.
- Пригодится: минимизация логических функций — общие сведения
- Пригодится: минимизация логических функций методом непосредственных преобразований
- Пригодится: минимизация логических функций методом Квайна
прибавлять
ПРИБАВЛЕНИЕ — ВЫЧИТАНИЕ
Прибавлять — вычитать
— Вся моя жизнь, — сказала Вера однажды, — это сначала прибавление, а потом вычитание, вычитание без конца. Малышев. Счастливая Капа.
ПРИБАВЛЯТЬ — УБАВЛЯТЬ
сов. прибавить — убавить
Прибавляться — убавляться ( см.)
прибавлять — сбавлять ( см.)
прибавляться — сбавляться
добавлять — убавлять ( см.)
добавляться — убавляться
набавлять — сбавлять
Ванечка, убавляя и прибавляя громкость , спрашивает: — А так, Шур. Шура, а вот так? М. Рощин. Шура и Просвирняк.
— Это хорошо, — сказал Батюк, — а то я было подумал: раз прибавим тебе два километра справа, попросишь настолько же убавить слева. К. Симонов. Последнее лето.
ПРИБАВЛЯТЬ — СБАВЛЯТЬ
сов. прибавить — сбавить
ПРИБАВЛЯТЬ — ОТНИМАТЬ
сов. прибавить — отнять
Ни отнять, ни прибавить — такая краса! До чего ж этот шар гончару удался! Кирсанов. Этот мир.
Счастье ума прибавляет, а несчастье последний отнимает. Пословица.
ДОБАВЛЯТЬ — УБАВЛЯТЬ
сов. добавить — убавить
ДОБАВЛЯТЬ — ИЗЫМАТЬ
сов. добавить — изъять
Кое-что пришлось добавить, кое-что изъять. Из гостиной был убран портрет хозяйского дедушки, а из кабинета поспешно изгнали восточного вида столик с перламутровой шахматной доской. В. Набоков. Защита Лужина.
Презентация на тему: » «Ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже». Леон Альберти (1404-1472) Руководитель проекта учитель МХК МБОУ СОШ п. Дружба Соколова.» — Транскрипт:
1
«Ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже». Леон Альберти ( ) Руководитель проекта учитель МХК МБОУ СОШ п. Дружба Соколова С.А.


3
«Человек измеряет землю и небо… Ни небо не представляется для него слишком высоким, ни центр Земли слишком глубоким… А так как человек познал строй небесных светил, то кто станет отрицать, что гений человека почти такой же, как у самого Творца небесных светил, и что он некоторым образом мог бы создать эти светила, если бы имел орудия и небесный материал…Человек может все». Марсилио Фичино. ( ) Согласны ли вы с высказыванием Марсилио Фичино?

4
Проторенессанс Джотто Воскрешение Лазаря «Джотто снова вывел на свет искусство, которое многие столетия было погребено под ошибками тех, кто, работая красками, более стремился забавлять глаза невежд, чем удовлетворять разуму мудрых» (Дж. Боккаччо). Насколько справедливы эти слова? Хотели бы вы что-то возразить их автору? Раннее Возрождение Сандро Боттичелли Благовещение «Редко какой художник так выражал духовное содержание своей эпохи» (П.П. Муратов). На сколько правомерная подобная оценка? Какие идеалы и образы своего времени запечатлел художник?

5
…Это почти рай. Ничего представить нельзя лучше впечатления этого неба, воздуха и света. Здесь есть такое солнце и небо и такие – действительно уж чудеса искусства неслыханного и невообразимого. Ф.М. Достоевский Назовите великих архитекторов эпохи Возрождения и их знаменитые архитектурные сооружения. Попробуйте разработать проект архитектурного сооружения в традициях идеального города Возрождения.

6
Леонардо да Винчи Рафаэль Джоконда 1503г. Мадонна Конестабиле гг. Микеланджело Пьета. Фрагмент гг. Вспомните названия произведений и их авторов

7
О ком эти высказывания? 1. «Обладал одновременно свойствами микроскопа и телескопа» (Эрвин Панофский историк искусства). 2. «Художник достойный бессмертия» (Эразм Роттердамский философ, писатель). 3. «Величайший гений среди сатириков» (Отто Бенеш известный искусствовед). 4. «Возрождал сны своего учителя и даже превосходил его» (Эрвин Панофский историк искусства).

8
1. Ян ван Эйк 2. Дюрер 3. Иеронимо Босх 4. Питер Брегель

9
Комедия дель арте Арлекин Коломбина Каждый актер выступал в определенной маске. Почему? Театр Шекспира Театр Шекспира нередко называют театром актера. Почему?

10
Попробуйте себя в работе – метод проектного обучения. Наша цель: воскресить античную формулу «красота – это гармония» и отразить сущность искусства эпохи Возрождения и своеобразное представление об окружающем мире. Основополагающий вопрос: «Ars longa, vita brevis» — «Жизнь коротка, искусство вечно»…?

11
Предлагаю попробовать себя в роли философов, искусствоведов и театралов.

12
Ожидаемые результаты: Группа философов – презентация через познание нового в сравнении. Группа искусствоведов – кластер (Титаны эпохи Возрождения). Группа театралов – организация театрального представления с применением монологической речи.

Примеры использования выражения «ни прибавить ни отнять»
Давайте рассмотрим несколько примеров использования выражения «ни прибавить ни отнять». Это выражение часто используется для подчеркивания точности, полноты или истинности утверждения.
- Пример 1: «Он описал ситуацию так, как она была — ни прибавить ни отнять». В этом случае автор утверждает, что его описание ситуации является абсолютной правдой, без преувеличений и искажений.
- Пример 2: «После трех месяцев подготовки я был готов к этому марафону — ни прибавить ни отнять». Здесь говорится о том, что говорящий был абсолютно уверен в своей физической и психологической подготовке к соревнованию.
- Пример 3: «Эта книга — шедевр литературы, ни прибавить ни отнять». Этот пример подчеркивает высокое качество литературного произведения и отсутствие каких-либо недостатков в тексте.
Выражение «ни прибавить ни отнять» может также использоваться, чтобы отразить чистую математическую точность результата. Например:
- Пример 1: «Это уравнение имеет решение 3 — ни прибавить ни отнять». Это утверждение подчеркивает, что результат является абсолютно точным.
- Пример 2: «После вычета налогов я получил точно 1500 долларов — ни прибавить ни отнять». Здесь говорящий подчеркивает, что его доход точно соответствует расчету.
Таким образом, выражение «ни прибавить ни отнять» используется в различных контекстах, чтобы подчеркнуть полноту, точность или истинность утверждения. Во всех случаях оно указывает на отсутствие возможности разногласий или ошибок в результатах или описании ситуации.
Поиск ответа
| Вопрос № 303833 |
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Если к 289 прибавить 311, то получится ровно 600. Если из 2791 вычесть 1475, то останется …. В порт вошел пароход с 2845 пассажирами. Сад разбит на 690 гектарах
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Ответ справочной службы русского языка
Выражения с переменными
Если в буквенном выражении буква обозначает величину, которая принимает не какое-то одно конкретное значение, а может принимать различные значения, то эту букву называют переменной и выражение называют выражением с переменной.
Определение.
Выражение с переменными – это буквенное выражение, в котором буквы (все или некоторые) обозначают величины, принимающие различные значения.
Например, пусть в выражении x2−1 буква x может принимать любые натуральные значения из интервала от до 10, тогда x – есть переменная, а выражение x2−1 есть выражение с переменной x.
Стоит отметить, что переменных в выражении может быть несколько. К примеру, если считать x и y переменными, то выражение является выражением с двумя переменными x и y.
Вообще, переход от понятия буквенного выражения к выражению с переменными происходит в 7 классе, когда начинают изучать алгебру. До этого момента буквенные выражения моделировали какие-то конкретные задачи. В алгебре же начинают смотреть на выражение более общо, без привязки к конкретной задаче, с пониманием того, что данное выражение подходит под огромное число задач.
В заключение этого пункта обратим внимание еще на один момент: по внешнему виду буквенного выражения невозможно узнать, являются ли входящие в него буквы переменными или нет. Поэтому ничто нам не мешает считать эти буквы переменными
При этом разница между терминами «буквенное выражение» и «выражение с переменными» исчезает.
Список литературы.
- Математика. 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
- Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
Как пишется «ни убавить ни прибавить» или «не убавить не прибавить»?
Как писать правильно выражение «ни убавить ни прибавить» или «не убавить не прибавить»? Через «ни» или через «не»? Какое правило?
В русском языке существует множество устойчивых выражений с повторяющимися частицами «ни». Написание таких выражений не регламентируется какими-либо правилами, а пишутся так благодаря сложившейся языковой традиции. Эти выражения надо запоминать.
К таким фразеологизмам относится и выражение «ни убавить ни прибавить». Пишется оно с повторяющимися частицами «ни», и это надо просто запомнить.
Слово «царевич» представляет собой существительное мужского рода в единственном числе. А для того чтобы определиться с постановкой мягкого знака после шипящего согласного «ч», нам придется вспомнить правило.
Кстати, существительные мужского рода: «плащ», «борщ», «ландыш», «меч», «ключ», «врач», «шалаш» тоже пишутся без «ь» после шипящих согласных.
Для того, чтобы определиться, как правильно писать: «когорта» или «кагорта«, нам следует установить происхождение этого слова и попытаться подобрать к нему проверочное слово.
В рассматриваемом слове нас интересует написание безударной гласной в первом слоге. Однако проверить правописание с помощью проверочного слова не выйдет, поскольку ни в одном из них ударение не падает на первый слог. Слово «cohors» позаимствовано из латинского языка. Поскольку в языке оригинале оно пишется через «о«, то и в русском языке его следует писать через гласную «о» ― «когорта«. Оно является словарным и его нужно запомнить.
Примеры предложений, в которых употребляется слово когорта:
У Грамоты.ру ответ такой же: очочки.
Многие наречия пишутся слитно или раздельно вне зависимости от каких-либо правил, а согласно определенным языковым традициям. Написание таких наречий регламентируется орфографическим словарем. К таким наречиям относится и наречие «допьяна». Оно пишется слитно и это надо запомнить.
Рассмотрим слово «с панталыку». Это наречие, так как отвечает на вопрос «как?». Образовано оно от существительного, хотя и слово «панталыку» в современном русском отдельно не употребляется. Согласно вышеупомянутому правилу, наречное выражение «с панталыку», образованное от существительного при помощи предлога «с» должно писать раздельно.
Ни убавить, ни прибавить
Смотреть что такое «Ни убавить, ни прибавить» в других словарях:
ни убавить ни прибавить — предик. разг. О соответствии одежды, обуви и т.п. размерам тела человека; как раз, в самый раз, впору. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
ни убавить ни прибавить — ни уб авить ни приб авить … Русский орфографический словарь
ни убавить ни прибавить — ни уба/вить ни приба/вить … Слитно. Раздельно. Через дефис.
Тут ни убавить, / ни прибавить — Из поэмы «За далью даль» (1960) советского поэта Александра Трифоновича Твардовского (1910 1971): Тут ни убавить, Ни прибавить, Так это было на земле. Энциклопедический словарь крылатых слов и выражений. М.: «Локид Пресс». Вадим Серов. 2003 … Словарь крылатых слов и выражений
УБАВИТЬ — УБАВИТЬ, убавлю, убавишь, совер. (к убавлять). 1. что и чего. Отнимая часть, уменьшить, понизить (общее количество чего нибудь), ослабить. Убавить цену. Убавить размеры. Убавить на рубль каждую сумму. Убавить длину на сантиметр. Убавить тягу в… … Толковый словарь Ушакова
УБАВИТЬ — УБАВИТЬ, влю, вишь; вленный; совер. 1. кого (что) и чего. Отняв часть, уменьшить, понизить; ослабить. У. премию. У. спеси. У. помощников. 2. что и чего. Уменьшить размер, вес, количество, скорость чего н. У. цену. У. шаг (пойти медленнее). У.… … Толковый словарь Ожегова
прибавить — глаг., св., употр. часто Морфология: я прибавлю, ты прибавишь, он/она/оно прибавит, мы прибавим, вы прибавите, они прибавят, прибавь, прибавьте, прибавил, прибавила, прибавило, прибавили, прибавивший, прибавленный, прибавив 1. см. нсв … Толковый словарь Дмитриева
ПРИБАВИТЬ — ПРИБАВИТЬ, прибавлю, прибавишь, совер. (к прибавлять). 1. что или чего. Сделать добавление к чему нибудь в каком нибудь количестве, дополнить что нибудь чем нибудь. Прибавить овса лошадям. Прибавить метр материи на платье. Прибавить пять рублей.… … Толковый словарь Ушакова
прибавить — добавить, присоединить, присовокупить, приобщить; примолвить; набавить, надбавить, накинуть; причислить, приплюсовать; увеличить, поднять, повысить, расширить, распространить, дополнить, обогатить, раздувать кадило, раздуть кадило, украсить,… … Словарь синонимов
убавить — прибавить повысить усилить … Словарь антонимов
Что такое буквенные выражения?
Понятие буквенных выражений дается практически сразу после знакомства с числовыми выражениями. Вводится оно примерно так. В некотором числовом выражении одно из чисел не записывается, а вместо него ставится кружочек (или квадратик, или нечто подобное), и говорится, что вместо кружочка можно подставить некоторое число. Для примера приведем запись . Если вместо квадратика поставить, например, число 2, то получится числовое выражение 3+2. Так вот вместо кружочков, квадратиков и т.п. условились записывать буквы, а такие выражения с буквами назвали буквенными выражениями. Вернемся к нашему примеру , если в этой записи вместо квадратика поставить букву a, то получится буквенное выражение вида 3+a.
Итак, если допустить в числовом выражении присутствие букв, которыми обозначены некоторые числа, то получится так называемое буквенное выражение. Дадим соответствующее определение.
Определение.
Выражение, содержащее буквы, которыми обозначены некоторые числа, называется буквенным выражением.
Из данного определения понятно, что принципиально буквенное выражение отличается от числового выражения тем, что может содержать буквы. Обычно в буквенных выражениях используются маленькие буквы латинского алфавита (a, b, c, …), а при обозначении углов – маленькие буквы греческого алфавита (α, β, γ, …).
Итак, буквенные выражения могут быть составлены из чисел, букв и содержать все математические символы, которые могут встречаться в числовых выражениях, такие как скобки, знаки корней, логарифмы, тригонометрические и другие функции и т.п. Отдельно подчеркнем, что буквенное выражение содержит по крайней мере одну букву. Но может содержать и несколько одинаковых или различных букв.
Теперь приведем несколько примеров буквенных выражений. Например, a+b – это буквенное выражение с буквами a и b. Вот другой пример буквенного выражения 5·x3−3·x2+x−2,5. И приведем пример буквенного выражения сложного вида: 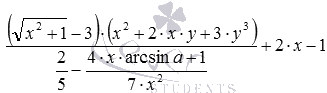 .
.
Тавтологии и противоречия
Логические тавтологии (или просто тавтологии) — это такие формулы логики высказываний,
что если буквы произвольным образом заменить высказываниями
(истинными или ложными), то в результате всегда получится истинное высказывание.
Так как истинность или ложность сложных высказываний зависит лишь от значений, а не
от содержания высказываний, каждому из которых соответствует определённая буква, то проверку того,
является ли данное высказывание тавтологией, можно подставить следующим способом. В исследуемом
выражении на место букв подставляются значения 1 и 0 (соответственно «истина» и «ложь») всеми возможными
способами и с использованием логических операций вычисляются логические значения выражений. Если все
эти значения равны 1, то исследуемое выражение есть тавтология, а если хотя бы одна подстановка даёт 0,
то это не тавтология.
Таким образом, формула логики высказываний, которая принимает значение «истина» при
любом распределении значений входящих в эту формулу атомов, называется тождественно истинной формулой
или тавтологией.
Противоположный смысл имеет логическое противоречие. Если все значения высказываний равны
0, то выражение есть логическое противоречие.
Таким образом, формула логики высказываний, которая принимает значение «ложь» при
любом распределении значений входящих в эту формулу атомов, называется тождественно ложной формулой
или противоречием.
Кроме тавтологий и логических противоречий существуют такие формулы логики высказываний,
которые не являются ни тавтологиями, ни противоречиями.
Пример 9. Составьте таблицу истинности для формулы логики высказываний
и определите, является ли
она тавтологией, противоречием или ни тем, ни другим.
Решение. Составляем таблицу истинности:
| И | И | И | И | И |
| И | Л | Л | Л | И |
| Л | И | Л | И | И |
| Л | Л | Л | Л | И |
В значениях импликации не встречаем строку, в которой из «истины» следует «ложь». Все
значения исходного высказывания равны «истине». Следовательно, данная формула логики высказываний является тавтологией.
Пример 10. Составьте таблицу истинности для формулы логики высказываний
и определите, является ли
она тавтологией, противоречием или ни тем, ни другим.
Решение. Составляем таблицу истинности:
| И | И | И | И | И | И |
| И | И | Л | И | Л | Л |
| И | Л | И | Л | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | Л | И | И |
| Л | И | Л | Л | Л | И |
| Л | Л | И | Л | И | И |
| Л | Л | Л | Л | Л | И |
Среди значений данного высказывания одно — «ложь», остальные — «истина». Следовательно, данная формула логики высказываний не является ни тавтологией, ни
противоречием.
- Пригодится: минимизация логических функций — общие сведения
- Пригодится: минимизация логических функций методом непосредственных преобразований
- Пригодится: минимизация логических функций методом Квайна
Числовые выражения – что это?
Знакомство с числовыми выражениями начинается чуть ли не с самых первых уроков математики. Но свое имя – числовые выражения – они официально приобретают немного позже. Например, если следовать курсу М. И. Моро, то это происходит на страницах учебника математики для 2 классов. Там представление о числовых выражениях дается так: 3+5, 12+1−6, 18−(4+6), 1+1+1+1+1 и т.п. – это все числовые выражения, а если в выражении выполнить указанные действия, то найдем значение выражения.
Можно сделать вывод, что на этом этапе изучения математики числовыми выражениями называют имеющие математический смысл записи, составленные из чисел, скобок и знаков сложения и вычитания.
Чуть позже, после знакомства с умножением и делением, записи числовых выражений начинают содержать знаки «·» и «:». Приведем несколько примеров: 6·4, (2+5)·2, 6:2, (9·3):3 и т.п.
Дальше числа увеличиваются, а числовые выражения становятся более разнообразными: 212·5−12·2, (515−225)·3−916:4·7 и так далее.
А в старших классах разнообразие записей числовых выражений разрастается как снежный ком, катящийся с горы. В них появляются обыкновенные и десятичные дроби, смешанные числа и отрицательные числа, степени, корни, логарифмы, синусы, косинусы и так далее.
Обобщим всю информацию в определение числового выражения:
Определение.
Числовое выражение — это комбинация чисел, знаков арифметических действий, дробных черт, знаков корня (радикалов), логарифмов, обозначений тригонометрических, обратных тригонометрических и других функций, а также скобок и других специальных математических символов, составленная в соответствии с принятыми в математике правилами.
Разъясним все составные части озвученного определения.
В числовых выражениях могут участвовать абсолютно любые числа: от натуральных до действительных, и даже комплексных. То есть, в числовых выражениях можно встретить
- натуральные числа 5, 172, 4,
- целые числа −17, , 63,
-
рациональные числа в виде
- обыкновенных дробей 1/2, ,
- смешанных чисел ,
- непериодических и периодических десятичных дробей 7,22 и −8,17(53),
- иррациональные числа ,
- а также комплексные числа с мнимой единицей .
Со знаками арифметических действий все понятно – это знаки сложения, вычитания, умножения и деления, имеющие соответственно вид «+», «−» , «·» и «:». В числовых выражениях может присутствовать один из этих знаков, некоторые из них или все сразу, и причем по нескольку раз. Вот примеры числовых выражений с ними: 3+6, 2,2+3,3+4,4+5,5, 41−2·4:2−5+12·3·2:2:3:12−1/12.
Что касается скобок, то имеют место как числовые выражения, в которых есть скобки, так и выражения без них. Если в числовом выражении есть скобки, то они в основном
- указывают порядок выполнения действий, например, 2·(2,3−1/5) или (1+2·(2−(5−4)))·(3−1,7);
- содержат отрицательное число, например, 5·(−2)+14:(−7) или ;
- отделяют аргумент функции, например, log2(3+15·4+1) или sin(π/2−π/6)+cos(π/4);
- отделяют основание степени, например, (2−1,3)2.
А иногда скобки в числовых выражениях имеют какое-нибудь определенное отдельно указанное специальное предназначение. К примеру, можно встретить квадратные скобки, обозначающие целую часть числа, так числовое выражение +2 обозначает, что к целой части числа 1,75 прибавляется число 2.
Из определения числового выражения также видно, что в выражении могут присутствовать степени, корни , логарифмы log, ln, lg, обозначения sin, cos, tg, ctg или arcsin, arccos, arctg, arcctg и т.п. Вот примеры числовых выражений с ними: tgπ, arcsin1+arccos1−π/2 и .
Деление в числовых выражениях может быть обозначено с помощью . В этом случае имеют место числовые выражения с дробями. Приведем примеры таких выражений: 1/(1+2), 5+(2·3+1)/(7−2,2)+3 и .
В качестве специальных математических символов и обозначений, которые можно встретить в числовых выражениях, приведем . Для примера покажем числовое выражение с модулем .
Посылки и выводы. Валидный и не валидный аргумент
Пусть есть высказывания, которые можно назвать посылками. Пусть также есть
высказывание, которое можно назвать выводом. Словосочетание «можно назвать» используется при условии,
что посылки связываются с выводом. То есть, из посылок логически следует вывод. Тогда, если посылки имеют значения «истина» и вывод тоже
имеет значение «истина», то аргумент является валидным. Если же посылки имеют значения «истина»,
а вывод имеет значение «ложь», то аргумент не является валидным. Синонимы понятия «валидность» (в
рассматриваемом здесь значении) — «логическая правильность», «резонность».
Пример валидного аргумента:
- Посылка. A и B — программисты
- Посылка. A и B разрабатывают программы для бухгалтеров
- Вывод. Есть программисты, которые разрабатывают программы для бухгалтеров
То есть, из посылок логически следует вывод.
Пример не валидного аргумента:
- Посылка. Запись числа может содержать запятую
- Посылка. В предложении может быть запятая
- Вывод. Есть числа, которые называются предложениями
То есть, из посылок логически не следует вывод.
Пример 12. Проверьте валидность аргумента, если
- Посылка.
- Посылка.
- Вывод.
Решение. Составляем таблицу истинности:
| И | И | Л | И | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | И | И | Л |
| Л | Л | И | И | И | И |
В третьей строке обе посылки истинны, а вывод — ложный. Следовательно, аргумент
не валидный. Таким образом, в аналогичных задачах подозрительными являются те строки, в которых все
посылки истинны. Если вывод также истинный, то аргумент валидный, если ложный, то аргумент не валидный,
как в этом примере. Если же посылки или обе ложны, или ложна одна из них, то такие строки не играют
роли в проверке аргумента на валидность, каким бы ни было значение вывода.





























