«пробочная» проблема или что такое реверсивное движение

Скорость при равномерном прямолинейном движении: формула

Одна из основных величин, задействованных в уравнении равномерного прямолинейного движения, — скорость. Она определяет характер наклона графика. Чем выше значение скорости, тем круче график. Если график направлен вниз, это означает: значение скорости имеет знак «-».

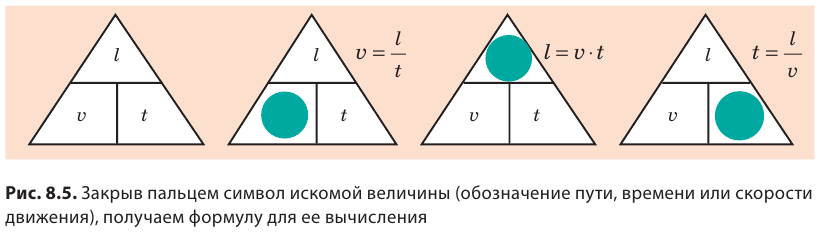
Величина, которая математически выражается отношением перемещения тела к промежутку времени, за который это перемещение произошло, — скорость (V) прямолинейного равномерного движения.

Примечание 1

Скорость имеет векторный характер. Ее направление совпадает с направлением конечного перемещения.

По своему определению, скорость — это отношение пути к отрезку времени, за которое произошло перемещение. Единицы измерения скорости определяются в зависимости от:

1. если движение выражается в метрах, а время — в секундах, то скорость измеряется в метрах в секунду. Это означает, что за одну секунду тело перемещается на определенное количество метров.
2. Движение — в км, а время — в часах, скорость — км/ч.

При равномерном движении скорость — величина постоянна на протяжении совершаемого перемещения.

Перемещение при прямолинейном равномерном движении

Формулы ПРД (прямолинейного равномерного движения) — основа для определения скорости и перемещения.

Вернемся к графику, на котором путь (S), пройденный телом за промежуток времени (t), определяется как проекция вектора перемещения на ось OX. Она равна X-Xo. Тогда перемещение (S)= X-Xo.

В то же время из вышеописанной формулы:

X(S)=Vt

Следовательно, V=S/t

Если записать данное выражение в векторной форме, станет понятно, что перемещение и скорость однонаправленны, а модуль перемещения составляет пройденный путь. Измерение перемещения производится в единицах длины: м, км, см и т.п.

Самыми простыми задачами в механической физике являются те, в которых требуется определить положение тела (в начале или конце движения), его скорость и время, на протяжении которого оно передвигалось. Сделать это можно с помощью формулы:

Примеры решения задач

Однако не при любом виде движения можно использовать данную формулу для определения перемещения. Существует ряд особенностей (рассмотрены ниже, в виде примеров), в которых действия имеют иной характер.

Задача 1

Каков модуль и каково направление скорости тела, если известно, что движение равномерно и происходит вдоль оси OX. С начала движения прошло 4 секунды, а координата изменилась с 5м до -3м.

Решение

Выше было рассмотрено, что отражением модуля и направления вектора являются проекции на оси координат. Поскольку движение характеризуется равномерностью, то проекцию скорости на ось абсцисс можно определить по следующей формуле:

Проекция может иметь отрицательный знак. В таком случае скорость точки иметь направление, противоположное положительному по оси OX. Модуль скорости \(V=|Vx|=|-2м/с|=2м/с.\)

Задача 2

Расстояние между пунктами A и B по прямой линии 20 км. Навстречу друг другу из этих пунктов одновременно выехали два автомобиля. Первый имел скорость 50 км/ч, второй — 60 км/ч.

Необходимо определить места положения автомобилей относительно пункта А через полчаса с момента начала движения, а также на каком расстоянии они будут друг от друга в этот момент.

Решение.

Автомобили совершают движения, которые можно выразить формулами:

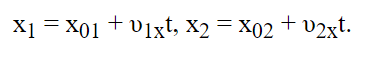
Спустя полчаса (0,5ч), их положение математически можно выразить так:

Один из автомобилей достигнет точки C, отдаленной от старта движения на 25 км вправо от A. Второй автомобиль достигнет точки D, которая отдалена влево на 10 км. Таким образом, модуль расстояния составит разность их координат:

\(S=|X2-X1| =|-10км-25км|=35км\)

Соответственно пройденные расстояния можно найти по формулам:

\(S1=V1t=50 км/ч*0,5ч=25км\)

\(S2=V2t=60 км/ч*0,5ч=30км\)

Задача 3

Автомобиль выехал из пункта A в пункт B со скоростью V1. Через время t0 пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V2. Расстояние между пунктами обозначаем S. Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?

Решение

Задача № 3

Автомобиль выехал из пункта A в пункт B со скоростью V₁. Через время t пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V₂.

Расстояние между пунктами обозначаем S.

Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?

Решение

При встрече автомобилей их координаты будут равны: X₁=X₂=X_в

В целом уравнения движения в данном случае выглядят так:

X₁=V₁t

X₂=S+V₂(t-t)

Производя математические действия, получаем:

V₁t_в=S+V₂(t_в-t)

Вероятно, V₁>V₂, S>V₂t

Место встречи автомобилей можно найти по формуле:

Физика движения: понятие и принципы

Физика движения — это раздел физики, который изучает движение тел и его характеристики. Движение — это перемещение тела относительно определенной точки или точки отсчета. Для изучения этого процесса в физике существуют основные понятия и принципы, которые помогают описать и предсказать движение тел.

Основные понятия в физике движения:

• Система отсчета — это точка или тело, относительно которого изучается движение других тел.
• Траектория — это путь, по которому перемещается тело в пространстве.
• Скорость — это величина, равная отношению пройденного пути к затраченному времени. Скорость может быть постоянной или изменяться со временем.
• Ускорение — это изменение скорости тела за единицу времени. Ускорение может быть положительным (если скорость увеличивается) или отрицательным (если скорость уменьшается).
• Инерция — это свойство тела сохранять свое состояние покоя или равномерного прямолинейного движения, пока на него не действует внешняя сила.

Принципы физики движения:

• Принцип относительности — закон, согласно которому движение тела может быть описано относительно любой другой системы отсчета. Это значит, что существование абсолютно неподвижной системы отсчета считается относительным.
• Принцип сохранения импульса — закон, согласно которому сумма импульсов системы тел остается неизменной, если на нее не действуют внешние силы.
• Принцип действия и противодействия (закон Ньютона) — закон, согласно которому на каждое действие существует противодействие равной величины, но противоположного направления.

Изучение понятий и принципов физики движения позволяет осознать и объяснить различные аспекты движения тел и позволяет прогнозировать и предсказывать результаты различных физических экспериментов.

Опасности для пешеходов и велосипедистов на дороге

Дорога – это место повышенной опасности для пешеходов и велосипедистов. Неправильные действия водителей, недостаточное освещение на улицах, а также невнимательность граждан могут приводить к страшным последствиям на дороге.

Пешеходы часто нарушают правила дорожного движения, переходят дорогу в неположенных местах, не соблюдают скоростной режим и не следят за своими детьми. Также повышенный риск возникает в условиях плохой видимости и при нехватке обзорности со стороны водителей.

Велосипедисты подвергаются риску во время движения на проезжей части, особенно на дорогах без велосипедной полосы. Не соблюдение правил дорожного движения и неисправные велосипеды могут стать причиной серьезных аварий.

Чтобы избежать опасностей на дороге, необходимо соблюдать правила дорожного движения, быть внимательными и осторожными, не совершать рискованных маневров. Водители должны уважать пешеходов и дать им дорогу на пешеходных переходах или в местах, где пешеходы собираются перейти дорогу.

• Соблюдение Правила 11 — проезд пешеходного перехода, обозначенного специальными дорожными знаками.
• Освещение дороги в темное время суток и в условиях плохой видимости, особенно в населенных пунктах.
• Проверка технического состояния велосипеда перед каждым поездкой.

Важно помнить, что забота о собственной безопасности на дороге – это забота не только о собственной жизни, но и о жизни окружающих

Советы водителю

• Перед перекрестком внимательно следите за знаками, установленными на нем и регламентирующими движение на следующем за ним участке дороги;
• Если вам нужно двигаться прямо, лучше не перестраиваться на трамвайные пути, особенно в час пик. Оставайтесь на своей полосе, чтобы не помешать своими маневрами движению общественного транспорта;
• Если вы перестроились на попутные трамвайные пути, чтобы совершить разворот, двигайтесь по дорожному полотну с рельсами непосредственно до перекрестка, подождите, когда пройдет встречный поток, а затем пересекайте пути встречного направления строго перпендикулярно.

Данное видео при помощи схем и пояснений к ним поведает вам о разрешенных маневрах при пересечении трамвайных путей:

Типы повреждений

Сила и поверхность удара

Повреждение будет разным для данных автомобилей одинаковой массы и имеющих одинаковую скорость в зависимости от объекта столкновения, например, столба или стены. Это может быть выражено уравнением
f = F / A,
где f – величина силы удара на единицу поверхности
F — сила
А – поверхность удара
Если удар приходится на большую поверхность, повреждение будет минимальным.
Наоборот, чем меньше поверхность удара, тем более серьезным будет повреждение. На примере справа бампер, капот, радиатор и т. д. серьезно деформированы. Двигатель сдвинут назад и последствия столкновения доходят до задней подвески.

Два типа повреждений

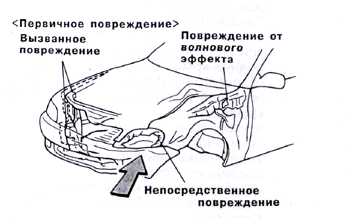Первичное повреждение

Столкновение между автомобилем и препятствием называется первичным столкновением, а создаваемое при этом повреждение — первичным повреждением.Непосредственное повреждение

Повреждение, вызываемое препятствием (внешней силой), называется непосредственным повреждением.Повреждения от волнового эффекта

Повреждения, создаваемые при передаче энергии удара, называются повреждениями от волнового эффекта.Вызванное повреждение

Повреждение, вызываемое в других частях, испытывающих растягивающее или толкающее усилие в результате непосредственного повреждения или повреждения от волнового эффекта, называется вызванным повреждением.

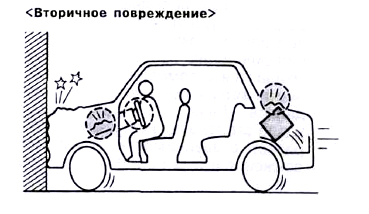Вторичное повреждение

Когда автомобиль сталкивается с препятствием, создается большая сила замедления, которая останавливает автомобиль в течение нескольких десятков или сотен миллисекунд. В этот момент пассажиры и предметы внутри салона автомобиля будут пытаться продолжать свое движение со скоростью автомобиля до столкновения. Столкновение, которое вызывается инерцией и которое имеет место внутри автомобиля, называется вторичным столкновением, а получающееся в результате этого повреждение называется вторичным (или инерционным) повреждением.

Категории нарушения положения частей конструкции

• Прямое смещение
• Косвенное (непрямое) смещение

Рассмотрим каждое из них отдельно

Особенности перемещения

Перемещение – это разность между начальной и конечной точкой расположения человека или предмета в пространстве после того как был преодолён какой-то путь.

Значение перемещения всегда является положительным, а также имеет чёткое направление.

Совпадение между перемещением и путём возможно только в том случае если путь был осуществлён по прямой линии, а направление при этом не изменялось.

С помощью перемещения можно рассчитать, где находился человек или предмет в определённый этап времени.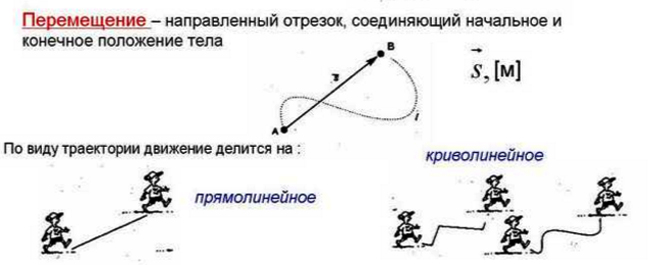

Для обозначения перемещения используют букву S, но поскольку перемещение является векторной величиной то над данной буквой ставится стрелочка →, которая и указывает на то, что перемещение – это вектор. К сожалению, увеличивает путаницу между путём и перемещением ещё тот факт, что оба понятия также можно обозначить буквой L.

Равномерное прямолинейное движение — коротко о главном

Сегодня ты узнал:

• Как решить основную задачу механики в общем виде;
• Равномерное прямолинейное движение — такое движение, при котором тело за любые равные промежутки времени совершает равные перемещения;
• Скорость равномерного прямолинейного движения есть физическая величина, равная отношению вектора перемещения ко времени, за которое оно произошло;
• Скорость равномерного прямолинейного движения постоянна;
• Как решить основную задачу механики для равномерного прямолинейного движения;
• Как строить и анализировать графики равномерного прямолинейного движения;
• Графиком равномерного прямолинейного движения является прямая;
• Встреча – такое событие, при котором координаты тел в один и тот же момент времени совпадают;
• Проекция перемещения тела численно равна площади под графиком скорости тела;
• Как строить траекторию движения тела;
• Средняя скорость тела – векторная физическая величина, равная отношению перемещения тела на определенном участке траектории ко времени, за которое оно совершено;
• Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден;
• Траектория движения тела зависит от выбора системы отсчета;
• Как доказать закон сложения скоростей;
• Абсолютная скорость есть векторная сумма относительной и переносной скоростей;

А еще ты научился решать задачи разного уровня сложности!

Ой, я что, не сказал? Там сложные были!

Упражнения по технике передвижения

Беговые упражнения.

1. Бег приставным шагом правым и левым боком вперёд. 2. Бег с высоким подниманием бедра 3. Семенящий бег 4. «Олений бег» 5. Бег с захлёстыванием голени. 6. Бег на прямых ногах с закидыванием пяток.

Беговые упражнения с изменением скорости.

1. Бег с коротким и длинным шагом. 2. Бег с изменением скорости, чередование медленного бега и коротких рывков. 3. Бег с ускорениями на месте и в движении. 4. Бег с изменением скорости и направления движения по звуковому сигналу тренера. 5. Бег скрестным и приставным шагом с ускорениями по звуковому сигналу тренера. 6. Бег с внезапными остановками, поворотами на 180 и 360 градусов с последующим ускорением вправо, влево и т.д.

Старты из статических исходных положений.

1. Старт из положения, сидя, полуприсидя, лёжа. 2. Старт из положения «упор руками» 3. Старт из положения «спиной вперёд» 4. Старт из высокой или низкой стартовой стойки.

Старты из динамических исходных положений.

1. Старт после ходьбы в глубоком приседе. 2. Старт после 100 прыжков на скакалке. 3. Стартовый рывок после подскоков в приседе на месте, в движении, вперёд, назад. 4. Старт из положения «ходьбы в приседе боком» 5. Старт после кувырков вперёд, назад и т.д

Старты после различных беговых и прыжковых упражнений.

По теме: Почему кружится голова после бега

1.Старт после бега с высоким подниманием бедра, после семенящего бега. 2. Старт после бега на прямых ногах с закидыванием пяток, после бега с захлёстыванием голени. 3. Старт после бега скрестным и приставным шагом. 4. Старт после бега спиной вперёд с поворотом на 180 градусов. 5. Старт после прыжковых упражнений.

Беговые упражнения с преодоление препятствий

1. Бег с обеганием стоек, флажков на максимальной скорости, препятствия расставленные на одной линии. 2. Тоже упражнение только препятствия расставлены в шахматном парядке или произвольно. 3. Тоже самое только спиной в перёд 4. Бег с имитацией удара головой после обегания каждого препятствия 5. Бег с имитацией обманного движения перед каждым препятствием (дриблинг)

Беговые упражнения с различными задачами.

1. бег с имитацией ударных движений головой, ногой. 2. Бег с имитацией движений подката, выбивания мяча, ложных движений 3. Бег в сочетании с прыжковыми упражнениями. Чередование прыжков на ногах с бегом. 4. Бег с различным положение рук: руки за спину, за голову. 5. Бег с преодолением сопротивления партнёра 6. Бег в различных эстафетах. Эстафеты с акцентом на отдельные физические качества.

Беговые упражнения в гору и с горы

1. Бег в максимальном темпе в гору, по пересечённой местности. 2. Бег в максимальном темпе в гору, руки за спину, руки на грудь. 3. Бег в гору спиной вперёд, правым и левым боком.Бег с горы с преодолением препятствий, поворотами, остановками, ускорениями

Советы по выбору попутного направления движения

1. Разведайте маршруты

Перед тем, как отправиться в путь, изучите возможные маршруты и узнайте, где находятся основные направления движения. Узнайте, какие трассы чаще всего используются, и выберите попутное направление.

2. Обратитесь за помощью

Если вы не уверены, какое направление выбрать, можете обратиться за помощью к опытным путешественникам или водителям. Они смогут дать вам подсказки и рекомендации, а также поделиться своими опытом и достоинствами разных направлений.

3. Используйте интернет

Интернет – отличный ресурс для поиска информации о попутных направлениях. Вы можете посетить специализированные форумы, где люди делятся своими путешествиями и опытом. Также существуют приложения и сайты для совместных поездок, где вы сможете найти других путешественников, едущих в нужное вам место.

4. Учитывайте время и сезон

При выборе попутного направления не забывайте учитывать время года и погодные условия. Некоторые направления могут быть недоступны или неудобны в определенное время года. Если вы планируете путешествовать на автомобиле, также учтите пробки и плотность движения на трассах.

5. Будьте гибкими

Иногда, чтобы выбрать попутное направление, нужно быть гибкими и открытыми для неожиданностей. Может получиться так, что самое интересное и удобное направление не будет совсем попутным, но при этом вы получите больше удовольствия и новых впечатлений.

6. Доверяйте интуиции

Важно слушать свою интуицию при выборе попутного направления. Если у вас есть ощущение, что определенное направление вам больше всего подходит, не стоит его игнорировать. Интуиция часто помогает найти те самые интересные и неповторимые места

Интуиция часто помогает найти те самые интересные и неповторимые места.

Возможность путешествовать попутно может стать отличной альтернативой классическим способам передвижения. Следуя приведенным советам, вы сможете выбрать попутное направление, которое позволит сэкономить деньги, получить новые знакомства и насладиться увлекательным путешествием.

ПРИМЕРЫ ЗАДАНИЙ

1) \( v_1=v_2 \) 2) \( v_1=2v_2 \) 3) \( 2v_1=v_2 \) 4) \( 1,2v_1=10v_2 \)

На рисунке изображена гистограмма. Она представляет собой расстояние, пройденное мухой (1) и воробьем (2) за одно и то же время, когда они движутся с одинаковой скоростью. Сравните их скорости \( v_1 \) и \( v_2 \).

1) \( v_1=v_2 \) 2) \( v_1=2v_2 \) 3) \( 3v_1=v_2 \) 4) \(2v_1=v_2)

На рисунке представлен график зависимости коэффициента скорости равномерного движения от времени. Мера перемещения тела за 2 с равна

1) 20 м 2) 40 м 3) 80 м 4) 160 м

Диаграмма на рисунке показывает расстояние, пройденное телом при равномерном движении, как функцию времени. Мера скорости тела равна

1) 0,1 м/с 2) 10 м/с 3) 20 м/с 4) 40 м/с.

На рисунке представлены графики зависимости расстояния от времени для трех тел. Сравните скорости \( v_1 \), \( v_2 \) и \( v_3 \) этих тел.

v_3 \) 3) \( v_1 4) \( v_1=v_2 \), \( v_3

8. какая из следующих диаграмм отражает связь между расстоянием и временем при равномерном движении тела?

9. на следующем рисунке изображена диаграмма координат тела как функция времени. Какова координата тела в момент времени 6 с?

1) 9,8 м

1) ​ \( v_1=v_2=v_3 \) ​ 2) \( v_1>v_2>

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​\( a_x \)​ > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​\( v_{0x} \)​ > 0, ​\( a_x \)​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_{0x} \) > 0, \( a_x \) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, \( v_{0x} \) < 0, \( a_x \) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​\( t_2-t_1 \)​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​\( n \)​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Кинематика

Раздел кинематики отвечает на вопросы о том, как именно происходит механическое движение тела.

Механическое движение 

Механическое движение — это перемещение тела с течением времени и относительно других объектов в пространстве. 

Для расчета этих изменений понадобится система отсчета, которая состоит из:

• объекта, относительно которого будет происходить отсчет движения;
• системы координат, в которой находится объект отсчета;
• часов (для измерения времени).

В системе отсчета метр является единицей длины, а секунда — единицей времени.

Другими важными определениями в кинематике являются:

1. Материальная точка — это объект, размеры которого можно не учитывать в расчетах.  
2. Траектория движения тела (линия, по которой движется объект).
3. Путь, пройденный телом (определенный участок траектории, пройденный объектом за определенное время).

Существует 2 вида движения согласно траектории:

• прямое;
• криволинейное.

Поступательное и вращательное движение твердого тела

В кинематике выделяют два вида движения:

• поступательное;
• вращательное.

Поступательное движение — это движение твердого тела, при котором все его точки проходят одну и ту же траекторию и в любой момент времени обладают одинаковыми по направлению и величине векторами скорости и ускорения, синхронно меняющихся для любой точки объекта.

Вращательное движение — это вид механического движения, при котором материальное тело проходит траекторию окружности. При этом все точки тела описывают окружности, которые находятся в параллельных плоскостях. Центры всех окружностей находятся на одной прямой, которая перпендикулярна к плоскостям окружностей (называется осью вращения).

Кинематические уравнения движения

Определение местоположения материальной точки в пространстве можно осуществить двумя способами:

• учитывая зависимость координат от времени;
• учитывая зависимость от времени радиус-вектора.

Эту зависимости можно представить в виде кинематических уравнений движения:

\(x=x\left(t\right) \)

\(y=y\left(t\right)\)

\(z=z\left(t\right)\)

или 

\(\vec r=\vec r\left(t\right)\)

Нулевой вектор на данной иллюстрации — это радиус-вектор положения точки в начальный момент времени.

Кинематические характеристики (скорость, ускорение)

Основными кинематическими характеристиками являются:

• скорость;
• ускорение.

Скорость \((\vec v)\) — это векторная величина, которая характеризует направление и быстроту движения.

Среднюю скорость можно вычислить по формуле:

\(\vec v=\frac{\Delta\vec r}{\Delta t}\)

где \(\Delta\vec r \) — перемещение, \(\Delta t\) — время, за которое это перемещение произошло.

Символом \(∆\) обозначается разность однотипных величин или совсем маленьких интервалов.

Мгновенная скорость может быть вычислена тогда, когда \(\Delta t\rightarrow0\) и вектор перемещения совпадает с путем перемещения:

\(\vec v=\frac{d\vec r}{dt}=\frac{dS}{dt}\)

Ускорение тела (a) является величиной, равной отношению изменения скорости движения тела к длительности промежутка времени, за которое это изменение скорости произошло. Оно рассчитывается по формуле:

\(a=\frac{\Delta V}{\Delta t}\)

Мгновенным ускорение будет являться тогда, когда среднее ускорение за промежуток ∆t → 0, м/с²:

\(a=\frac{dv}{dt}\)