Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 2 | 1 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0.428 | ||
| x | 2 | |
| 0.856 | ||
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0.848 | ||
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0.25 | ||
| x | 2 | |
| 0.5 | ||
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0.768 | ||
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Слайд 5Преимущества троичной симметричной системы (-1, 0, 1)естественное представление чисел со
знаком (не нужен прямой, обратный или дополнительный код!)знак числа —
это знак старшей ненулевой цифры и не нужен знаковый битПростое сравнение чисел по величине, при этом не нужно смотреть на знакпоэтому команда ветвления по знаку в троичной машине работает вдвое быстрее, чем в двоичнойусечение длины числа равносильно правильному округлению (округление в двоичных машинах не обеспечивают этого)троичный сумматор осуществляет вычитание при инвертировании одного из слагаемых, откуда следует, что троичный счетчик автоматически является реверсивным (обеспечивает и сложение и вычитаниев трехвходовом троичном сумматоре перенос в следующий разряд возникает в 8 ситуациях из 27, а в двоичном сумматоре — в 4 из 8. В четырехвходовом сумматоре перенос также происходит только в соседний разряд. таблицы умножения и деления почти так же просты, как и в двоичной системеумножение на -1 инвертирует множимоетрехуровневый сигнал более устойчив к воздействию помех в линиях передачи. Это означает что специальные методы избыточного кодирования троичной информации проще, нежели двоичной

4.13. Как представляются в компьютере вещественные числа?
Система вещественных чисел в математических вычислениях предполагается
непрерывной и бесконечной, т.е. не имеющей ограничений на диапазон и
точность представления чисел. Однако в компьютерах числа хранятся в регистрах и
ячейках памяти с ограниченным количеством разрядов. В следствие этого система
вещественных чисел, представимых в машине, является дискретной (прерывной) и
конечной.
При написании вещественных чисел в программах вместо привычной запятой
принято ставить точку. Для отображения вещественных чисел, которые могут быть
как очень маленькими, так и очень большими, используется форма записи чисел с порядком
основания системы счисления. Например, десятичное число 1.25 в этой форме
можно представить так:
1.25 . 10
= 0.125 . 101 = 0.0125 . 102
= …
или так:
12.5 . 10-1
= 125.0 . 10-2 = 1250.0 . 10-3
= … .
|
Любое число N в системе счисления с основанием q |
Если «плавающая» точка расположена в мантиссе перед первой
значащей цифрой, то при фиксированном количестве разрядов, отведённых под
мантиссу, обеспечивается запись максимального количества значащих цифр числа,
то есть максимальная точность представления числа в машине. Из этого следует:
|
Мантисса должна быть правильной дробью, у которой |
Мантиссу и порядок q-ичного числа принято записывать в системе с
основанием q, а само основание — в десятичной системе. Примеры
нормализованного представления:
Десятичная
система
Двоичная система
753.15 = 0.75315 . 103;
—101.01 = —0.10101 . 211
(порядок 112 = 310)
— 0.000034 = — 0.34 . 10-4;
0.000011 = 0.11 . 2-100 (порядок
—1002 = —410).
Вещественные числа в компьютерах различных типов записываются по-разному,
тем не менее, все компьютеры поддерживают несколько международных стандартных
форматов, различающихся по точности, но имеющих одинаковую структуру следующего
вида:

Здесь порядок n-разрядного нормализованного числа задается в так
называемой смещенной форме: если для задания порядка выделено k
разрядов, то к истинному значению порядка, представленного в дополнительном
коде, прибавляют смещение, равное (2k-1 — 1).
Например, порядок, принимающий значения в диапазоне от —128 до +127, представляется
смещенным порядком, значения которого меняются от 0 до 255.
Использование смещенной формы позволяет производить операции над порядками,
как над беззнаковыми числами, что упрощает операции сравнения, сложения и
вычитания порядков, а также упрощает операцию сравнения самих нормализованных
чисел.
Чем больше разрядов отводится под запись мантиссы, тем выше точность
представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от
наименьшего отличного от нуля числа до наибольшего числа, представимого в
машине при заданном формате.
|
Стандартные форматы представления вещественных чисел: 1) одинарный — 32-разрядное нормализованное число со 2) двойной — 64-разрядное нормализованное число со 3) расширенный — 80-разрядное число со знаком, |
Следует отметить, что вещественный формат с m-разрядной мантиссой
позволяет абсолютно точно представлять m-разрядные целые числа, т. е. любое
двоичное целое число, содержащее не более m разрядов, может быть без
искажений преобразовано в вещественный формат.
Двоичная (бинарная) система счисления
Двоичная (или бинарная) система счисления — это позиционная система счисления с основанием 2.
Принцип считать двумя цифрами берёт своё начало ещё в Древнем Китае. Но развитие современной бинарной системы началось в XVII веке, а применение нашлось только в середине XX века.
История двоичной системы счисления
В 1605 году английский астроном и математик Томас Хэрриот описал двоичное представление чисел, а философ Фрэнсис Бэкон создал шифр из двух символов — A и B.
В 1670 году испанский богослужитель Хуан Карамюэль-и-Лобковиц опубликовал представление чисел в разных системах счисления, в том числе и двоичной.
Но самым значительным событием стали работы немецкого математика Готфрида Лейбница, который в 1703 году описал двоичную арифметику — математические операции с двоичными числами.
В 1838 году американский изобретатель Сэмюэл Морзе создал одноимённый шифр, содержащий два символа: «точка» и «тире». Их можно было передавать по телеграфу в виде длинных и коротких сигналов. Азбука Морзе не была бинарной системой в строгом смысле слова, но двоичный принцип впервые показал свою значимость.
В 1847 английский математик Джордж Буль изобрёл «булеву алгебру», в которой было два понятия («ложь» и «истина»), а также ряд логических законов.
В 1937 году американский инженер Клод Шеннон объединил бинарный принцип, булеву логику и электрические схемы и ввёл понятие «бит» — минимальное количество информации:
- — ложь — нет тока (0 бит);
- 1 — истина — есть ток (1 бит).
С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.
Числа в двоичной системе счисления
Двоичное число — это число, состоящее из двоичных цифр. А у нас их всего две. Принято обозначать и 1, но, как показала практика, это могут быть и два разных значения: «лампа горит» и «лампа не горит», «ток» и «нет тока» и так далее.
В следующей таблице приведены числа в двоичной системе (зелёный столбец) и соответствующие им числа в других часто используемых системах счисления — восьмеричной, десятичной и шестнадцатеричной.

Изображение: Лев Сергеев для Skillbox Media
Преимущества и недостатки двоичной (бинарной) системы счисления
Явные минусы двоичной системы обусловлены тем, что на интуитивном уровне людям она чужда — в отличие, например, от десятичной. И это — первый недостаток. Пройдёмся по остальным:
Длинная запись, неудобство с большими числами. Возьмём, к примеру, обозначение белого цвета в RGB-палитре: 25510, 25510, 25510 (здесь и далее нижний индекс указывает основание системы — двоичная, десятичная и так далее). Значения цветов принято записывать в шестнадцатеричной системе счисления (FF16, FF16, FF16). Если перевести это в бинарный вид, получится громоздко и непонятно:
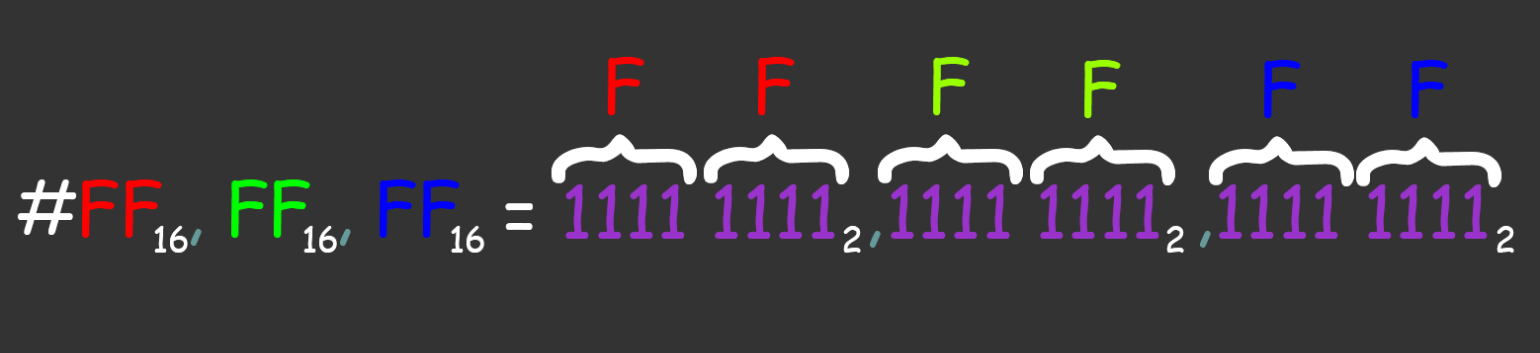
Изображение: Лев Сергеев для Skillbox Media
- Долгое время ручных вычислений.
- Не применяется в повседневной жизни (если, конечно, вы не компьютер).
А вот для ЭВМ бинарочка — как родная. И отсюда следуют её плюсы:
- Позиционная система, имеет разряды.
- Применимы арифметические действия.
- Можно построить логику.
- Подходит для шифровки данных.
- Родной язык компьютерных систем.
4.11. Как представляются в компьютере целые числа?
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака
Обычно занимают в памяти компьютера один
или два байта. В однобайтовом
формате принимают значения от 000000002
до 111111112. В двубайтовом формате —
от 00000000 000000002 до 11111111
111111112.
Диапазоны значений
целых чисел без знака
|
Формат числа в |
Диапазон |
|
|
Запись с порядком |
Обычная запись |
|
|
1 |
0 … 28-1 |
0 … 255 |
|
2 |
0 … 216-1 |
0 … 65535 |
Примеры:
а) число 7210 = 10010002 в однобайтовом
формате:
![]()
б) это же число в двубайтовом формате:
![]()
в) число 65535 в двубайтовом формате:
![]()
Целые числа со знаком
Обычно занимают в памяти компьютера один, два или четыре байта, при этом
самый левый (старший) разряд содержит информацию о знаке числа.
Диапазоны значений
целых чисел со знаком
|
Формат числа в |
Диапазон |
|
|
Запись с порядком |
Обычная запись |
|
|
1 |
-27 … |
-128 … 127 |
|
2 |
-215 … |
-32768 … 32767 |
|
4 |
-231 … |
-2147483648 … |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового
формата, при котором для знака отводится один разряд, а для цифр абсолютной
величины — семь разрядов.
|
В компьютерной технике применяются три формы записи |
Последние две формы применяются особенно широко, так как позволяют упростить
конструкцию арифметико-логического устройства компьютера путем замены
разнообразных арифметических операций операцией cложения.
Положительные числа в прямом,
обратном и дополнительном кодах изображаются одинаково — двоичными
кодами с цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом,
обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды
цифровой части числа — двоичный код его абсолютной величины. Например:
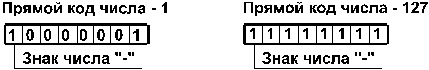
2. Обратный код. Получается инвертированием всех цифр двоичного кода
абсолютной величины числа, включая разряд знака: нули заменяются единицами, а
единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с
последующим прибавлением единицы к его младшему разряду. Например:
![]()
Обычно отрицательные десятичные числа при вводе в машину автоматически
преобразуются в обратный или дополнительный двоичный код и в таком виде
хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из
машины происходит обратное преобразование в отрицательные десятичные числа.
Системы счисления – виды, особенности
Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.
Все существующие системы делят на 2 группы:
- Позиционные системы счисления – такие, в которых, в зависимости от положения, цифры будет иметь разное значение. К этой группе относится арабская СС, в которой на первом месте справа цифра будет обозначать единицы, на втором – десятки, на третьем – сотни и так далее.
Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.
К этой группе также относятся СС с различными основаниями (2,8,16).
- Непозиционные СС – имеет значение именно знак, а не его положение. Единицы, десятки, сотни обозначаются определенными символами. Яркий представитель этой группы – римская СС.
Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.
12 – XII
8 – VIII или IIX
Правильным считается тот вариант, при котором получается меньше символов.
Интересно. Первой позиционной СС была вавилонская и была она шестидесятеричная! А в 19 веке использовали двенадцатеричную СС.
Алфавит СС – знаки, которые используются для обозначения цифр.
Основание – количество знаков, которыми кодируются числа. Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.
Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 12548, 011001112
Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).
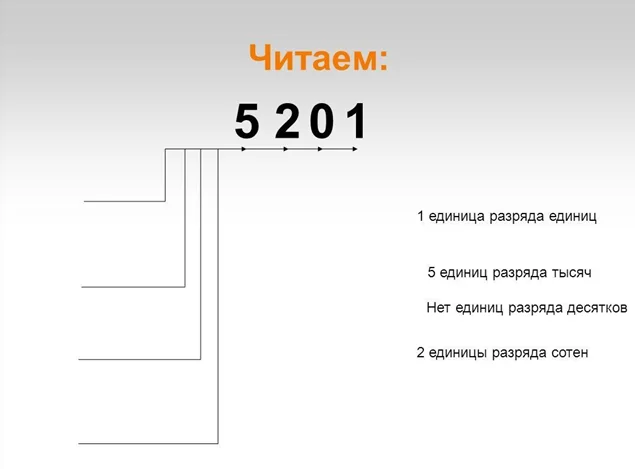
Разряд – положение, позиция обозначения цифры в числе. Пример?
Как перевести десятичную дробь в обыкновенную
Чтобы перевести десятичную дробь в обыкновенную, числитель запишите как число после запятой. Знаменатель – разрядная единица с количеством нулей, равным количеству знаков после запятой.
Например, . Сократите дробь, если возможно: .
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 7/20.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
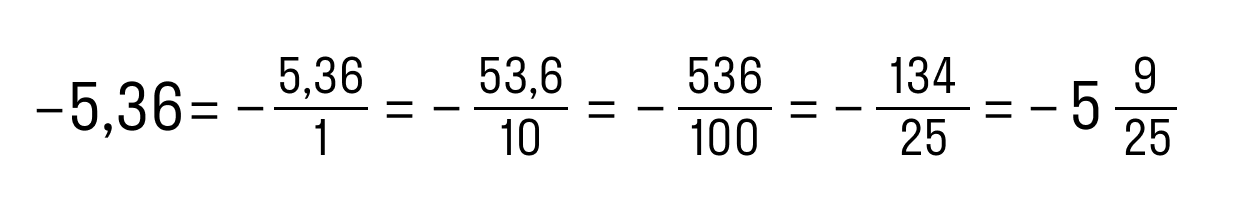
|
Еще алгоритм: как преобразовать десятичную дробь в обыкновенную
|
Вот и всё! Эта схема значительно проще и быстрее. Проверим:
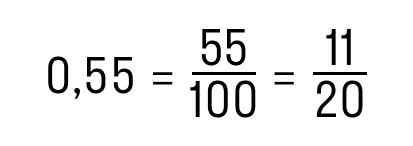
Методы поиска десятичных эквивалентов чисел
Существует несколько методов, которые можно использовать для поиска десятичных эквивалентов чисел. Каждый из этих методов имеет свои особенности и может быть полезен в разных ситуациях.
1. Деление числа на 10 в степени n:
Для поиска десятичного эквивалента числа можно разделить его на 10, возведенное в нужную степень n. Например, если нужно найти десятичный эквивалент числа 25 в десятичной системе счисления, можно разделить 25 на 10 в степени 2 (так как в десятичной системе счисления позиции цифр увеличиваются в 10 раз с каждой следующей позицией).
Для этого нужно выполнить следующие шаги:
- Разделить число на 10, возведенное в степень n.
- Округлить полученное значение до нужной точности (обычно до определенного количества знаков после запятой).
- Полученное значение будет являться десятичным эквивалентом исходного числа.
2. Использование таблицы десятичных эквивалентов:
Для некоторых чисел, таких как десятичные доли или обыкновенные дроби, можно использовать специальные таблицы десятичных эквивалентов. В этих таблицах указано, какие числа соответствуют определенным десятичным дробям или долям.
Чтобы найти десятичный эквивалент числа с помощью таблицы, нужно найти соответствующую десятичную дробь или долю в таблице и использовать ее значение.
3. Использование калькулятора:
Если у вас есть доступ к калькулятору, его можно использовать для поиска десятичного эквивалента числа. В большинстве калькуляторов есть функция, которая позволяет переводить числа из одной системы счисления в другую. Нужно только ввести исходное число и выбрать десятичную систему счисления. Калькулятор автоматически найдет десятичный эквивалент.
Эти методы могут быть полезны при работе с числами и переводе их из одной системы счисления в другую
Важно помнить, что точность десятичного эквивалента зависит от выбранного метода и заданной точности округления
4.14. Как компьютер выполняет арифметические действия над нормализованными числами?
К началу выполнения арифметического действия операнды операции помещаются в
соответствующие регистры АЛУ.
Сложение и вычитание
При сложении и вычитании сначала производится подготовительная операция,
называемая выравниванием порядков.
|
В процессе выравнивания порядков мантисса числа с меньшим |
В результате выравнивания порядков одноименные разряды чисел оказываются
расположенными в соответствующих разрядах обоих регистров, после чего мантиссы
складываются или вычитаются. В случае необходимости полученный результат
нормализуется путем сдвига мантиссы результата влево. После каждого сдвига
влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0.10111 . 2-1
и 0.11011 . 210. Разность порядков слагаемых здесь
равна трем, поэтому перед сложением мантисса первого числа сдвигается на три
разряда вправо:
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101
. 210 и 0.11101 . 21. Разность
порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед
вычитанием мантисса второго числа сдвигается на один разряд вправо:
Результат получился не нормализованным, поэтому его мантисса
сдвигается влево на два разряда с соответствующим уменьшением порядка на
две единицы: 0.1101 . 2.
Умножение
|
При умножении двух нормализованных чисел их порядки |
Пример 3. Выполнить умножение двоичных нормализованных чисел:
(0.11101 . 2101)
. (0.1001 . 211) = (0.11101 . 0.1001)
. 2(101+11) = 0.100000101 . 21000.
Деление
|
При делении двух нормализованных чисел из порядка делимого |
Пример 4. Выполнить деление двоичных нормализованных чисел:
0.1111 . 2100
: 0.101 . 211 = (0.1111 : 0.101) . 2(100-11)
= 1.1 . 21 = 0.11 . 210.
Использование представления чисел с плавающей точкой существенно усложняет
схему арифметико-логического устройства.
Что такое системы счисления
С давних пор людям нужно было записывать числа. В торговле числа нужны, чтобы знать, сколько товаров есть на складе и сколько денег принесла сделка. Записи о положении небесных тел помогли шумерам составить первый календарь, а календарь, в свою очередь, пригодился, чтобы заранее готовиться к посевным и сбору урожая. Строительные сметы, переписи населения, распределение наследства — числа оказались очень востребованными даже в самых древних государствах.
Так что люди научились записывать числа в незапамятные времена. Небольшие числа легко записывались зарубками или насечками, но если в числе несколько знаков, требуется иная система записи. Эту проблему в разных странах решали по-разному.
Сейчас разные способы записи чисел называются системами счисления.
Систем счисления было придумано довольно много, и даже в наши дни мы используем две системы, возникшие в далёкой древности. Из Древнего Рима к нам пришла римская система счисления, где цифры обозначаются буквами латинского алфавита. За основу римляне взяли количество пальцев на одной руке — 5, и на двух руках — 10. Числа 1, 5 и 10 в римской системе обозначаются буквами I, V и X, и с помощью них можно записать любое число от 1 до 49. Например, VII это 7, а XIX — 19.
От Древних Шумеров мы научились делить дроби на шестьдесят частей. Именно из-за них в нашем часе 60 минут, а в минуте 60 секунд. Шумерская система счисления так и называется — шестидесятеричная. Но, конечно, наиболее привычной выглядит численная запись в системе, которую придумали в Древней Индии. Сейчас ее называют арабской или десятичной системой счисления.



























