Множество простых чисел
Множествами называются совокупности элементов, объединенных в одно целое общими свойствами.

Для изучаемых объектов к ним относятся:
-
принадлежность к натуральным;
-
наличие максимум двух делителей.
Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему.
Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее.
По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным.
В итоге, все составные окажутся зачеркнутыми.
Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.
Проблемы Ландау
Насчёт простых чисел выдвинуто очень много интересных гипотез. Среди них видное место занимают гипотезы Ландау (проблемы Ландау). Формулируются они так:
1. Гипотеза Гольдбаха
Можно ли любое целое чётное число, большее 2, записать в виде суммы двух простых?
2. Гипотеза о числах-близнецах
Бесконечно ли число простых p таких, что p + 2 тоже простое?
3. Гипотеза Лежандра
Всегда ли существует по меньшей мере одно простое число, лежащее между двумя последовательными полными квадратами?
4. Гипотеза о почти квадратных простых числах
Существует ли бесконечно много простых чисел p вида .
Проблемы Ландау ни доказаны, ни опровергнуты по состоянию на 2020 год. Далее кратко расскажу про каждую из них.
1. Гипотеза Гольдбаха
Существуют две гипотезы Гольдбаха: слабая (тернарная) и сильная (бинарная).
Слабая гипотеза Гольдбаха: Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.
Эту гипотезу доказал Харольд Гельфготт в 2013 году используя так называемые большие дуги. Финальная часть доказательства заняла 133 страницы.
Сильная гипотеза Гольдбаха: Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.
Надо заметить, что в обоих случаях гипотезы Гольдбаха простые числа не обязательно должны быть различными.
Заметьте, что в сильной гипотезе речь идёт только о чётных числах. Давайте покажем, что нечётное число не обязано быть представимо в виде суммы двух простых чисел. Просто приведём пример. Число 11 не представимо в виде суммы двух простых. Вроде бы несложно.
Но переформулируем проблему так: существует ли такое число, что любое нечётное, большее этого числа, представимо в виде суммы двух простых чисел? Давайте проверим. Пусть существует некоторое нечётное натуральное число N, такое, что любое нечётное число представимо в виде суммы двух простых чисел.
Возьмём произвольное нечётное . По предположению существуют такие простые p1 и p2, что . Если сумма двух натуральных чисел нечётна, то это значит, что одно из слагаемых чётно, а другое нет. Пусть для определённости p1 – чётное. Единственное чётное простое число — это 2. Значит, . То есть, K-2 (предыдущее перед K нечётное число) является простым. Поскольку всё вышесказанное верно для любого нечётного большего N, то получается, что все нечётные числа, начиная с N-2, являются простыми. Это неверно. Если бы это было так, то при n→ ∞. Однако, как говорилось выше при n→ ∞.
Итак, не существует такого числа, начиная с которого все нечётные числа могут быть представлены в виде суммы двух простых.
А что же насчёт чётных? Гипотеза не была опровергнута, не было найдено ни одного контрпримера. Но это не значит, что их не существует. Доказать же гипотезу полностью пока никому не удалось.
2. Гипотеза о числах-близнецах
Бесконечно ли число простых чисел близнецов?
Для начала сформулируем определение. Два простых числа называются близнецами если отличаются друг от друга на 2.
Примеры: 5 и 7, 11 и 13, 41 и 43.
Чэнь Цзинжунь доказал, что существует бесконечно много чисел p таких, что p+2 — простое или полупростое. Полупростое число — число, представимое в виде произведения двух простых чисел.
Так же доказано, что существует бесконечно много простых чисел, разница между которыми составляет 246. Это наилучшая из обоснованных на данный момент оценок. Если же использовать некоторые недоказанные гипотезы о простых числах, то оценку можно улучшить.
3. Гипотеза Лежандра
Всегда ли существует, по меньшей мере, одно простое число, лежащее между двумя последовательными полными квадратами?
Аналогичная гипотеза доказана для кубов, начиная с некоторого n. То есть, существует, по меньшей мере, одно простое число, лежащее между и для достаточно большого n. Для квадратов же, гипотеза Лежандра пока не доказана.
4. Почти квадратные простые числа
Существует ли бесконечно много простых чисел p вида ?
Можно точно утверждать, что не существует простых чисел вида , кроме p = 3. Действительно, , где множители — различные натуральные числа, отличные от 1 и от n во всех случаях кроме n = 2. Значит число вида составное для всех . А вот с числами вида всё немного сложнее. Однако удалось, например, доказать, что существует бесконечно много чисел вида , которые являются или простыми, или полупростыми.
Что такое взаимно простые числа
Взаимно простыми могут быть как два целых числа, так и их большее количество. Для начала введем определение для двух чисел, для чего нам понадобится понятие их наибольшего общего делителя. Если нужно, повторите материал, посвященный ему.
Определение 1
Взаимно простыми будут два таких числа a и b , наибольший общий делитель которых равен 1 , т.е. НОД (a , b) = 1 .
Из данного определения можно сделать вывод, что единственный положительный общий делитель у двух взаимно простых чисел будет равен 1 . Всего два таких числа имеют два общих делителя – единицу и минус единицу.
Какие можно привести примеры взаимно простых чисел? Например, такой парой будут 5 и 11 . Они имеют только один общий положительный делитель, равный 1 , что является подтверждением их взаимной простоты.
Если мы возьмем два простых числа, то по отношению друг к другу они будут взаимно простыми во всех случаях, однако такие взаимные отношения образуются также и между составными числами. Возможны случаи, когда одно число в паре взаимно простых является составным, а второе простым, или же составными являются они оба.
Это утверждение иллюстрирует следующий пример: составные числа — 9 и 8 образуют взаимно простую пару. Докажем это, вычислив их наибольший общий делитель. Для этого запишем все их делители (рекомендуем перечитать статью о нахождении делителей числа). У 8 это будут числа ± 1 , ± 2 , ± 4 , ± 8 , а у 9 – ± 1 , ± 3 , ± 9 . Выбираем из всех делителей тот, что будет общим и наибольшим – это единица. Следовательно, если НОД (8 , − 9) = 1 , то 8 и — 9 будут взаимно простыми по отношению друг к другу.
Взаимно простыми числами не являются 500 и 45 , поскольку у них есть еще один общий делитель – 5 (см. статью о признаках делимости на 5). Пять больше единицы и является положительным числом. Другой подобной парой могут быть — 201 и 3 , поскольку их оба можно разделить на 3 , на что указывает соответствующий признак делимости.
На практике довольно часто приходится определять взаимную простоту двух целых чисел. Выяснение этого можно свести к поиску наибольшего общего делителя и сравнению его с единицей. Также удобно пользоваться таблицей простых чисел, чтобы не производить лишних вычислений: если одно из заданных чисел есть в этой таблице, значит, оно делится только на единицу и само на себя. Разберем решение подобной задачи.
Пример 1
Условие:
выясните, являются ли взаимно простыми числа 275 и 84 .
Решение
Оба числа явно имеют больше одного делителя, поэтому сразу назвать их взаимно простыми мы не можем.
Вычисляем наибольший общий делитель, используя алгоритм Евклида: 275 = 84 · 3 + 23 , 84 = 23 · 3 + 15 , 23 = 15 · 1 + 8 , 15 = 8 · 1 + 7 , 8 = 7 · 1 + 1 , 7 = 7 · 1 .
Ответ:
поскольку НОД (84 , 275) = 1 , то данные числа будут взаимно простыми.
Как мы уже говорили раньше, определение таких чисел можно распространить и на случаи, когда у нас есть не два числа, а больше.
Определение 2
Взаимно простыми целые числа a 1 , a 2 , … , a k , k > 2 будут тогда, когда они имеют наибольший общий делитель, равный 1 .
Иными словами, если у нас есть набор некоторых чисел с наибольшим положительным делителем, большим 1 , то все эти числа не являются по отношению друг к другу взаимно обратными.
Возьмем несколько примеров. Так, целые числа − 99 , 17 и − 27 – взаимно простые. Любое количество простых чисел будет взаимно простым по отношению ко всем членам совокупности, как, например, в последовательности 2 , 3 , 11 , 19 , 151 , 293 и 667 . А вот числа 12 , − 9 , 900 и − 72
взаимно простыми не будут, потому что кроме единицы у них будет еще один положительный делитель, равный 3 . То же самое относится к числам 17 , 85 и 187: кроме единицы, их все можно разделить на 17 .
Обычно взаимная простота чисел не является очевидной с первого взгляда, этот факт нуждается в доказательстве. Чтобы выяснить, будут ли некоторые числа взаимно простыми, нужно найти их наибольший общий делитель и сделать вывод на основании его сравнения с единицей.
Пример 2
Условие:
определите, являются ли числа 331 , 463 и 733 взаимно простыми.
Решение
Сверимся с таблицей простых чисел и определим, что все три этих числа в ней есть. Тогда их общим делителем может быть только единица.
Ответ:
все эти числа будут взаимно простыми по отношению друг к другу.
Пример 3
Условие:
приведите доказательство того, что числа − 14 , 105 , − 2 107 и − 91 не являются взаимно простыми.
Решение
Начнем с выявления их наибольшего общего делителя, после чего убедимся, что он не равен 1 . Поскольку у отрицательных чисел те же делители, что и у соответствующих положительных, то НОД (− 14 , 105 , 2 107 , − 91) = НОД (14 , 105 , 2 107 , 91) . Согласно правилам, которые мы привели в статье о нахождении наибольшего общего делителя, в данном случае НОД будет равен семи.
Ответ:
семь больше единицы, значит, взаимно простыми эти числа не являются.
Виды чисел
- Натуральные – все положительные числа, которые мы используем для счета (2, 19, 56, 478, 2048 и т.д.). Ноль не является натуральным числом.
- Простые – натуральные числа, которые без остатка делятся только на единицу и само себя: 2, 3, 5, 7, 11 и т.д.
- Составные – числа, которые имеют три и более делителя.
- Целые – это положительные (больше нуля) и отрицательные (меньше нуля) числа, которые не имеют дробной части.
- Четные – целые числа, которые без остатка делятся на два: 2, 4, 6, 8, 10, 12 и т.д.
- Нечетные – целые числа, которые не делятся без остатка на два: 15, 21, 37, 41 и т.д.
- Вещественные – рациональные и иррациональные числа.
- Рациональные – числа, которые можно представить в виде обыкновенной дроби.
- Иррациональные – бесконечные непериодические десятичные дроби, которые нельзя представить в виде обыкновенных.
Это числа, которые используются при счете: 1, 2, 3… и т.д.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Это конечные дроби и бесконечные периодические дроби.
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Комплексные числа
Комплексные числа– числа, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i2 = -1. Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики, теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные.
При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Более общими (но всё ещё счётными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).
Т. е. множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. Множество рациональных чисел входит во множество действительных чисел. А множество действительных чисел входит во множество комплексных чисел.
Это высказывание можно проиллюстрировать с помощью кругов Эйлера: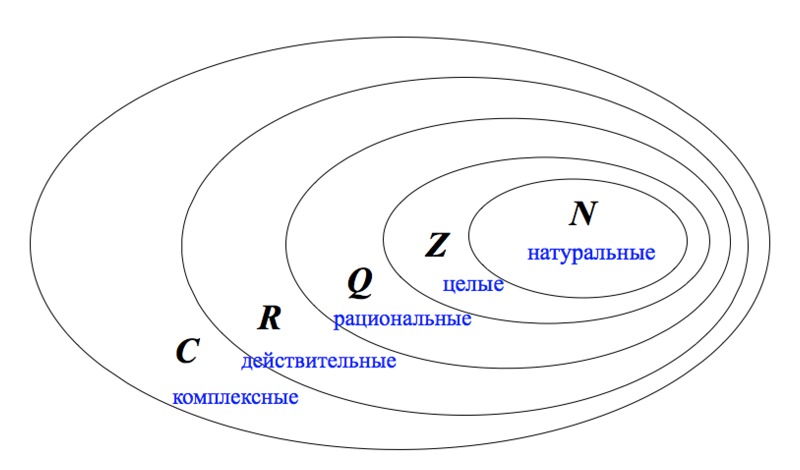
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
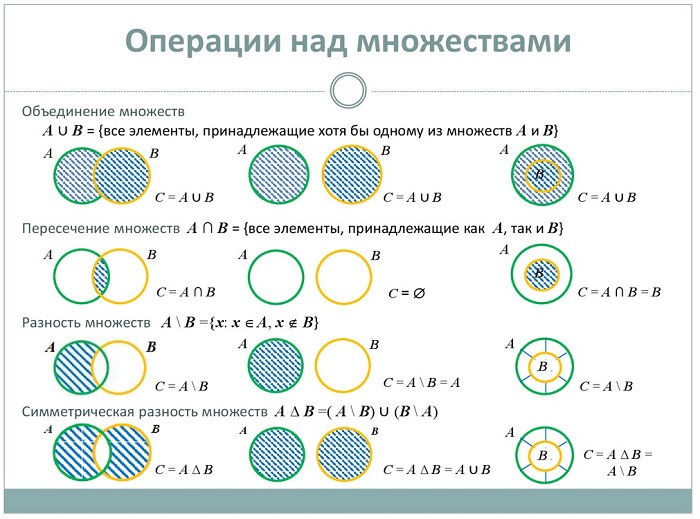
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Геометрический алгоритм Евклида
Данный алгоритм часто применяется для решения задач по нахождению наибольшего общего делителя двух чисел (целых). Алгоритм работает следующим образом:
Возьмем 2 целых числа и обозначим их как a и b. Представим числа в виде отрезков. Каждый из них имеет свое числовое значение.
- Из большего отрезка нужно вычесть меньший;
- Больший отрезок заменим полученной разностью величин;
- Продолжаем вычитать из большего отрезка меньший, пока они не станут равны;
- Процедуру вычитания проводим до тех пор, пока отрезки не станут равны.
Если в итоге получаем отрезки равной величины, то значит, что они соизмеримы. И последний полученный результат — это и есть показатель их наибольшей общей меры.
Если общей меры отрезков нет, то процесс будет продолжаться бесконечно.
Метод использования алгоритма Евклида. Найдем НОД двух чисел 1071 и 462. Представим и в виде буквенных обозначений. Пусть, a = 1071, b = 462.
Из 1071 вычтем 462 кратное число раз. Это можно сделать 2 раза. Количество раз, которое можно вычесть наименьшее число из большего обозначим буквой q.
1071 – 462 ⋅ 2 = 147
Из наименьшей величины (все, как в алгоритме Евклида) вычтем кратное число раз разность.
462 – 174 ⋅ 3 = 21
И снова проделываем аналогичное вычисление.
147 – 21 ⋅ 7 = 0
Последний остаток в данном примере = 21. Следовательно, НОД для чисел 1071 и 462 =21. Делаем вывод, что 21 > 1, значит данные числа не будут взаимно простыми.
Теперь можно попробовать применить данную формулу на практике.
Пример
Условие: нужно выяснить, являются ли числа 275 и 84 взаимно простыми или нет.
И то, и то число, точно имеют больше 1 делителя. Сразу сказать, что они взаимно простые нельзя. Для вычисления НОД применим алгоритм Евклида:
275 = 84 ⋅ 3 + 23 , 84 = 23 ⋅ 3 + 15 , 23 = 15 ⋅ 1 + 8 , 15 = 8 ⋅ 1 + 7 , 8 = 7 ⋅ 1 + 1 , 7 = 7 ⋅ 1
Ответ: Так как, НОД чисел 84 и 275 равен 1, то взаимная простота чисел доказана.
Если есть числовой ряд с большим количеством чисел и у всех у них наибольшим делителем является единица, то они будут проявлять свойство взаимной простоты по отношению друг к другу.
Количество чисел не имеет значение. Их может быть сколько угодно много. Главное – наибольший общий делитель – единица. Для наглядности, возьмем ряд чисел: 2, 3, 11, 19, 667. Они все делятся только сами на себя и на 1. Из это следует, что их свойство взаимной простоты доказано.
Примеры
Условие: определить наличие взаимной простоты у чисел 331, 463, 733 или опровергнуть ее.
Решение:
Используем для решения таблицу простых чисел. Проверим данные числа и таблицу. Да, в таблице можно встретить
их все. Это значит, что общим делителем чисел будет 1.
Ответ: все числа находятся в таблице простых чисел. Их наибольший делить -1. Значит все они взаимно
простые друг к другу.
Докажите, что следующие числа не являются взаимно простыми (105, — 14, — 2007, — 91).
Решение:
- Нужно найти общий наибольший делитель. Это можно сделать любым удобным способом;
- Вспоминаем, что отрицательные числа имеют те же делители, что и положительные.
- НОД для всех чисел будет = 7.
Ответ: 7 больше 1. Значит, что числа не будут являться взаимно простыми.
Пример
Определим, являются ли взаимно простыми числа 1729 и 282
Определение начинается с разложения на множители:
Обратите внимание, что для разложения таких чисел придется использовать метод перебора. Согласно таблице простых чисел каждый множитель проверяется, после чего деление продолжается
Подбирать множители нужно от маленьких чисел к большим, то есть от 2 и выше.
Как видно, общих множителей у двух чисел нет. Это значит, что числа можно считать взаимно простыми. Не нужно пугаться, если среди множителей попадаются достаточно большие числа. Среди учеников существует миф, что простые числа редко бывают больше 20, это не так. Просто такие числа проще использовать в задачах, чтобы набить руку. На экзамене или в контрольной сложность числа для разложения может быть абсолютно любой
Оценка сложности
бит
def atkins(limit):
primes = * limit
sqrt_limit = int( math.sqrt( limit ) )
x_limit = int( math.sqrt( ( limit + 1 ) / 2 ) )
for x in xrange( 1, x_limit ):
xx = x*x
for y in xrange( 1, sqrt_limit ):
yy = y*y
n = 3*xx + yy
if n <= limit and n%12 == 7:
primes = not primes
n += xx
if n <= limit and n%12 in (1,5):
primes = not primes
if x > y:
n -= xx + 2*yy
if n <= limit and n%12 == 11:
primes = not primes
for n in xrange(5,limit):
if primes:
for k in range(n*n, limit, n*n):
primes = False
return + filter(primes.__getitem__, xrange(5, limit))
Если кто улучшит этот алгоритм, или напишит ему альтернативу, буду очень рад!Наблюдения:Использованная литература:
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
\(a / b\) = \(a \times b^{-1}\), где \(b^{-1}\) — это обратный элемент к \(b\).
Определение: \(b^{-1}\) — это такое число, что \(bb^{-1} = 1\)
Утверждение: в кольце остатков по простому модулю \(p\) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к \(2\) по модулю \(5\) это \(3\) (\(2 \times 3 = 1 \pmod 5\)))
Задание
Найдите обратный элемент к: * числу \(3\) по модулю \(5\) * числу \(3\) по модулю \(7\) * числу \(1\) по модулю \(7\) * числу \(2\) по модулю \(3\) * числу \(9\) по модулю \(31\)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток \(1, 2, \ldots, (p-1)\) умножить на ненулевой остаток \(a\), то получатся числа \(a, 2a, \ldots, (p-1)a\) — и они все разные! Они разные, потому что если \(xa = ya\), то \((x-y)a = 0\), а значит \((x — y) a\) делится на \(p\), \(a\) — ненулевой остаток, а значит \(x = y\), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть \(1\), причем ровно один раз. А значит существует ровно один обратный элемент \(a^{-1}\). Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за \(O(p)\).
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > \(a^{p-1} = 1 \pmod p\), если \(p\) — простое, \(a \neq 0 \pmod p\)).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел \(1, 2, \ldots, (p-1)\) и \(a, 2a, \ldots, (p-1)a\) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: \((p-1)! = a^{p-1} (p-1)! \pmod p\).
\((p-1)!\neq 0 \pmod p\) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число — значит умножить на обратный к нему, который существует).
А значит, \(a^{p — 1} = 1 \pmod p\).
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что \(a^{p-2}\) — это обратный элемент к \(a\), а значит мы свели задачу к возведению \(a\) в степень \(p-2\), что благодаря быстрому возведению в степень мы умеем делать за \(O(\log p)\).
Обобщение У малой теоремы Ферма есть обобщение для составных \(p\):
Теорема Эйлера: > \(a^{\varphi(p)} = 1 \pmod p\), \(a\) — взаимно просто с \(p\), а \(\varphi(p)\) — это функция Эйлера (количество чисел, меньших \(p\) и взаимно простых с \(p\)).
Доказывается теорема очень похоже, только вместо ненулевых остатков \(1, 2, \ldots, p-1\) нужно брать остатки, взаимно простые с \(p\). Их как раз не \(p-1\), а \(\varphi(p)\).
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера \(\varphi(p)\) и найти \(a^{-1} = a^{\varphi(p) — 1}\).
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти \(a^{-1} \pmod p\), \(a\) и \(p\) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
\
Они есть и находятся расширенным алгоритмом Евклида за \(O(\log p)\), так как \(НОД(a, p) = 1\), ведь они взаимно простые.
Тогда если взять остаток по модулю \(p\):
\
А значит, найденный \(x\) и будет обратным элементом к \(a\).
То есть надо просто найти \(x\) из решения того уравнения по модулю \(p\). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.
Математика Эратосфена. Простые и составные числа
Решето Эратосфена — это специальный алгоритм, который позволяет определять все простые числа до целого заданного натурального числа N. Само название методики содержит основной принцип ее функционирования. «Решето» представляет собой «фильтр», пропускающий все ненужные числа, кроме простых.
Так, при составлении «решета» – таблицы, необходимо учитывать, что для выполнения задачи важна проверка чисел в последовательном порядке – начиная с двух и до 100, 1000 и т.д. Если у числа невозможно разложить на простые множители и делители отсутствуют – оно фиксируется в таблице, а если оно является натуральным составным числом, значит необходимо его исключить.
Составляя таблицу простых чисел в привычном порядке приходится поэтапно рассматривать каждую цифру. Необходимо начать с 2 – у нее можно выделить два делителя (1 и 2), поэтому оно является простым числом и может быть занесено в таблицу. Число 2, также, заносим в таблицу. Число 4 можно разложить на простые множители 2 и 2, а значит, в таблице его быть не должно, поскольку оно является составным. А 5 имеет всего два делителя, соответственно, оно фиксируется в таблице. Так, поочередно рассматривается каждое число, вплоть до 100, 1000, 10000 и т, д.
Данная методика является понятной, но весьма долгой и неудобной. Именно решето Эратосфена принято считать оптимальным алгоритмом. Далее, на примере приведенных таблиц будет рассмотрен сам алгоритм.
Найдем все простые натуральные числа от 2 до 50. Для начала, в таблицу заносятся все числа, которые располагаются в указанном числовом ряду
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 12 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
(Рис.2).
Далее выполняется последовательное зачеркивание всех чисел, кратных 2 (Рис.3).
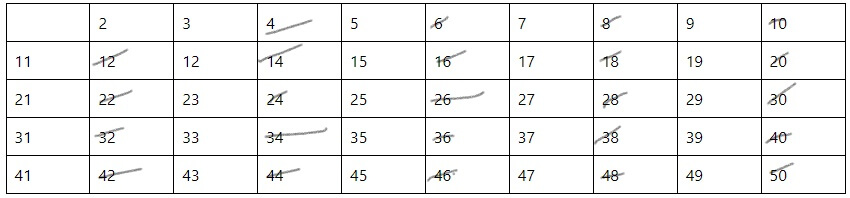 Рис. 3 Зачеркивание чисел, кратных двум
Рис. 3 Зачеркивание чисел, кратных двум
Затем, необходимо поочередно вычеркнуть все числа, кратные 3 (Рис. 4).
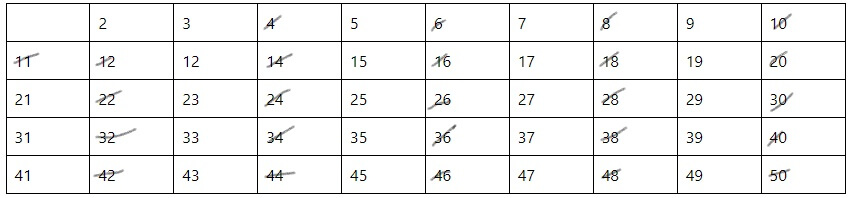 Рис. 4. Зачеркивание чисел, кратных 3
Рис. 4. Зачеркивание чисел, кратных 3
Также, необходимо поступить с числами, которые кратны 5 (Рис. 5).
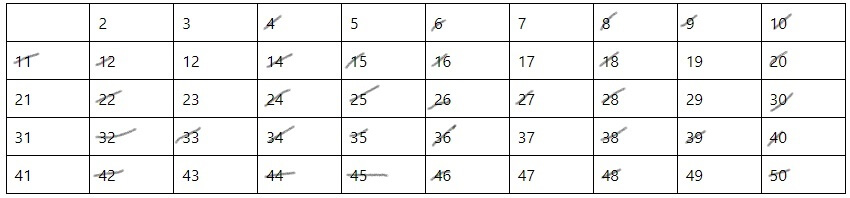 Рис. 5. Зачеркивание чисел, кратных 5
Рис. 5. Зачеркивание чисел, кратных 5
На последнем этапе зачеркиваются числа, кратные 7 и 11 (Рис. 6). В итоге будет получена окончательная таблица натуральных простых чисел от 2 до 50.
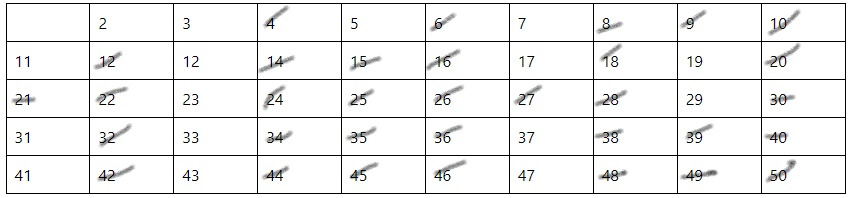 Рис. 6. Зачеркивание чисел, кратных 7 и 11
Рис. 6. Зачеркивание чисел, кратных 7 и 11
Далее стоит остановиться на формулировке Теоремы 3 и ее доказательстве.
Теорема 3
Наименьший положительный и отличный от 1 делитель основного числа a
не превосходит √a, где √a арифметическим корнем заданного числа.
Доказательство 3
Необходимо обозначить b наименьший делитель составного числа a. Существует такое целое число q, где a=b·q, причем имеем, что b≤q. Недопустимо неравенство вида b>q, так как происходит нарушение условия. Обе части неравенства b≤q следует умножить на любое положительное число b, не равное 1. Получаем, что b·b≤b·q, где b2≤a и b≤√a
Доказанная теорема показывает, что при поочередном вычеркивании чисел из таблицы, необходимо начинать с числа, которое будет равно b² и должно соответствовать неравенству b² ≤ a. Если вычеркивание начнется с чисел, кратных 2, то в первую очередь будет вычеркнуто число 4, а если с кратных 3, то – число 9.
Используя методику Эратосфена при составлении простой числовой таблицы, можно обнаружить, что в процессе вычеркивания натуральных составных чисел, останутся лишь те простые числа, которые не будут превосходить значение квадратного корня из n.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Задачи и доказательства
Числа a1, a2, …, akу, у которых есть положительный НОД, больший 11, не являются между собой взаимно обратными. Пример с последующей проверкой: 99, 17−99, 17 и −27−27 — простые. Любое количество цифр будет ВПЧ по отношению к другим членам совокупности. Но 12, −9, 90012, −9, 900 и −72−72 к этой категории не относятся.
Первое задание
Нужно найти число из 4 цифр, кратное 15. Это не дробь, знаменателя нет, но произведение составляющих равняется 60. Решение: чтобы результат делился на 15 без остатка, он должен делиться на 3 и 5. Из предполагаемого списка вычёркивается нуль, так как произведение бы равнялось 0, что невозможно. Можно прийти к выводу, что последняя цифра результата — 5.

Известно, что в ответе должно быть четыре цифры, из которых одна уже известна. Нужно найти оставшиеся три, которые находятся в ряду перед пятёркой, а при их умножении получается 12. Проверка предположения: 60:5=12. Полученный результат легко представить в виде нескольких вариантов со следующими тремя множителями:
- 1, 3 и 4;
- 1, 2 и 6;
- 2, 2 и 3.
По условию задачи, результат должен делиться на 15. Поэтому ответ будет состоять из трёх вариантов: 3225, 2325 и 2235.
Второй пример
Из 181615121 нужно зачеркнуть 3 цифры так, чтобы результат был кратным 12. Множители делителя: 3 и 4. Если их вычеркнуть, заданное число разделится на три и четыре, что объясняется их ПД:
- M кратно 4, если последние две цифры равны нулю либо их сумма делится на четыре без остатка.
- Если сумма составляющих цифр делится на три, тогда и само число кратно трём.
Учитывая ПД на 4, можно прийти к выводу, что последние две цифры из заданного числа не делятся на четыре. Поэтому из 181615121 вычёркивается единица.
Воспользовавшись признаками делимости на 3 и 4, можно составить следующие уравнения:
- 25 = 3×8 + 1. Если вычеркнуть один, условия задачи не будут соблюдены, так как нужно удалить ещё две цифры.
- 25 = 3×7 + 4. Не подходит, так как при сложении не получается 4.
- 25 = 3×6 + 7. Если вычеркнуть шестую цифру либо единицу, кроме последней, сумма двух удалённых из списка будет равна семи.
Ответ: 181512, 811512 либо 181152.
Третье и четвёртое задания
Пример 3: необходимо определить шестизначное число, для записи которого используются 0 и 6, а также оно делится на 90. Решение: составляется уравнение 90 = 10х9. Результат делится на 9 и 10. В конце находится нуль, а сумма составных цифр делится на девять. Для записи используются три шестёрки, так как 3 х 6=18, а 18 кратно 9. Ответы: 666000, 660600, 606060, 600660.

Пример 4: нужно определить четырёхзначное число, которое делится на 45 без остатка. Все составные цифры разные и нечётные. Решение: следует составить уравнение с учётом условия задачи. Так как 45 = 9х5, то результат делится на пять и на девять. Одновременно он должен оканчиваться на 5, так как нуль считается чётным. Первые три цифры: 1, 3, 7, 9. Из списка выбираются те три числа, которые в сумме с пятёркой делятся на 9. К ним относятся: 1, 3, 9 и 5. Ответы: 9135, 3915,1935, 1395, 3195.
Другое понятие, которое встречается в задачах на рассматриваемую тему — совокупность ПЧ. Такие цифры всегда попарно и взаимно простые. Пример последовательности: 1, 443, 857, 99171, 443, 857, 991. У любой такой последовательности понятия попарности и взаимности совпадают.





























