Свойство корня как функции
На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.
То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:
Теперь определим свойства функции корня и построим ее график.
Основные свойства корня как функции:
Промежуток [0; +∞) – является областью определения.
Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.
Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.
Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.
Значит можно утверждать, что:
Теперь можно построить график функции корня.
Пользуясь графиком, можно записать оставшиеся свойства функции.
На промежутке [0; +∞) функция возрастает.
Сверху функция не ограничена, но она ограничена снизу, например, прямой у, которая = -0,5.
На всей области определения функция выпукла вверх.
У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.
Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.
Тогда:
В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0.
Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
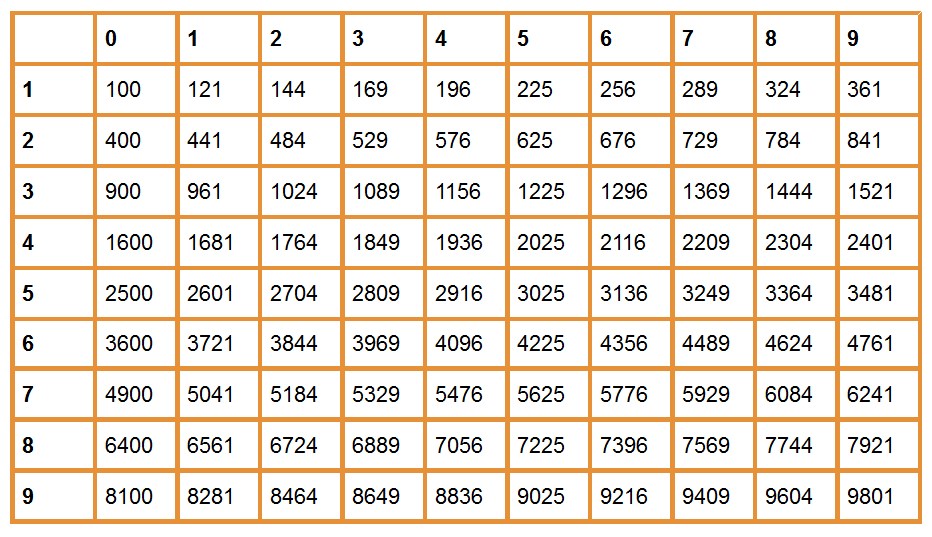
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
102 = 100
202 = 400
302 = 900
402 = 1600
502 = 2500
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 402и 502.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей
12 = 1
22 = 4
32 = 9
42 = 16 ⇒ 6
52 = 25 ⇒ 5
62 = 36 ⇒ 6
72 = 49 ⇒ 9
82 = 64 ⇒ 4
92 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 442 и 462.
Далее вычисляем: 44 * 44 = 1936.
46 * 46 = 2116.
Ответ: √2116 = 46
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
11666 : 4 = 2916
2916 : 4 = 729
729 : 3 = 243
243 : 3 = 81
| 11664 | 4 |
| 2916 | 4 |
| 729 | 3 |
| 243 | 3 |
| 81 | 81 |
Запишем выражение в следующем виде:
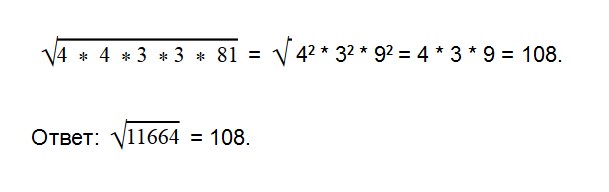
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- Вычислите значение квадратного корня: √36
- Вычислите значение квадратного корня: √64*36
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение выражения: 4√16 — 12
- Вычислите значение выражения: 5√9 — 8
- Вычислите значение выражения: 7√25 — 10
- Вычислите значение квадратного корня:
- Вычислите значение квадратного уравнения:
- Вычислите значение квадратного уравнения:
- Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем:7056 4 1764 4 441 3 147 3 49 7 7 7 1 - Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - Вычислите значение квадратного корня:
Как решаем:
= 0,09 - Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - Внесите множитель под знак корня: 6√7
Как решаем: √62 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - Упростите выражение: (5 — √2)2
Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2)2 = 27 — 10√2. - Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
Подбор числа перед корнем: полезные советы
Когда мы решаем задачи, связанные с корнями, нередко нам нужно подобрать число перед корнем. Как выбрать это число правильно? Ниже приведены несколько полезных советов, которые помогут вам справиться с этой задачей.
1. Учитывайте знак числа под корнем: Обычно, если число под корнем отрицательное, ответом будет мнимое число. Если число положительное, то ответ будет действительным числом.
2. Рассмотрите простые числа: В некоторых задачах перед корнем может стоять простое число. Например, если перед корнем стоит число 2, значит, ответом будет корень квадратный из этого числа.
3. Применяйте факторизацию: Если число можно разложить на простые множители, разделите его на один из этих множителей и добавьте корень из множителя в ответ. Например, если перед корнем стоит число 12, можно разделить его на простой множитель 2 и добавить корень из 2.
4
Обратите внимание на ближайшие квадраты: Приближение числа под корнем до ближайшего квадрата может помочь в подборе числа перед корнем. Например, если число под корнем 21, ближайший квадрат — 25
Можно использовать число 5 перед корнем.
Запомните эти советы и применяйте их при подборе числа перед корнем. Они помогут вам решить задачи с корнями и получить правильный ответ.
Действия с корнями: основы
Пример 1
650-28+512
Алгоритм действия:
Упростить подкоренное выражение. Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня
Обращаем ваше внимание, что второй множитель заносится под знак корня.
После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Нельзя складывать или вычитать подкоренные числа!
Пример 2
Давайте попробуем решить данный пример:
650=6(25×2)=(6×5)2=302. Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 302.
28=2(4×2)=(2×2)2=42. Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 42.
512=5(4×3)=(5×2)3=103. Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 103.
Результат упрощения: 302-42+103
302-42+103=(30-4)2+103=262+103.
Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
Пример 3
(45)+45:
- Упрощаем (45). Раскладываем 45 на множители: (45)=(9×5);
- Выносим 3 из-под корня (9=3):45=35;
- Складываем множители у корней: 35+45=75.
Пример 4
640-310+5:
- Упрощаем 640. Раскладываем 40 на множители: 640=6(4×10);
- Выносим 2 из-под корня (4=2):640=6(4×10)=(6×2)10;
- Перемножаем множители, которые стоят перед корнем: 1210;
- Записываем выражение в упрощенном виде: 1210-310+5;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12-3)10=910+5.
Пример 5
95-23-45
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
(9-4)5-23=55-23.
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3+(2x)1/2.
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Уничтожение иррациональности в знаменателе
Чтобы избавиться от иррациональности в знаменателе, нужно домножить на одно и то же выражение числитель и знаменатель дроби, пользуясь по мере надобности формулами сокращённого умножения. Если в знаменатетеле дроби корень числа — домножаем на такой же корень, и в знаменателе оказывается само число.
7 / √(5) =
= 7 × √(5) / 5
Если в знаменателе дроби сумма/разность корней двух чисел — домножаем на разность/сумму этих корней, и в знаменателе оказывается разность самих чисел.
7 / =
= 7 × / =
= 7 × / 4
Если в знаменателе сумма/разность кубических корней двух чисел — домножаем на неполный квадрат разности/суммы этих кубических корней. В знаменателе получается сумма/разность самих чисел.Если в знаменателе неполный квадрат суммы/разности кубических корней двух чисел — домножаем на разность/сумму этих кубических корней. В знаменателе получается разность/сумма самих чисел.
5 / =
= 5 × / =
= 5 × / 11
Поразрядное нахождение значения корня
Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.
Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.
Пример 1:
Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:
1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).
2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.
3. Значение сотых. По аналогии находим приближенное значение к 7.
2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.
Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.
Задания для отработки материала
1 задание
а)√324
б)√900
в)√1369
2 задание
а)³√531,441
б)³√166,375
3 задание
а) ⁵√-14 2471/1024
б) ⁵√-5 1182/3125
4 задание
а)Найдите квадратный корень из 3.
б)Найдите квадратный корень из 5.
в)Найдите квадратный корень из 9.
Ответы с решением
1 задание
а)√324
1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:
2)2×3×3=18. Получается, √324=18.
б)√900
1)2×2×3×3×5×5=2²×3²×5²=√900.
Извлекаем:
2)2×3×5=30. Мы получили √900=30.
в)√1369
1)37×37=37²=√1369.
А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.
2 задание
а)³√531441.
1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.
Разложили на простые множители, а теперь найдем квадратный корень.
2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.
3)1000=10³.
4)³√531441/³√1000=81/10=8,1.
б)³√166,375.
1) 5×5×5×11×11×11=5³×11³=³√166375.
2)5³×11³=55. Так как числа в кубе – они в степени 1.
3) 1000=10³.
4)³√166375/³√1000=55/10=5,5.
3 задание
а)
1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.
2) -⁵√14 2471/1024= -⁵√16801/1024.
3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.
4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.
б)
1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.
2) -⁵√5 1182/3125= -⁵√16807/3125.
3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.
4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.
4 задание
а)√3≈1,73.
б√5≈2,23.
в)√8≈2,82.
Определение корня

Корень может быть как целым числом, так и десятичной дробью. Чтобы понять его значение, нужно уметь читать корни правильно. Правила чтения корня – это набор правил, которые помогают определить, какой корень скрывается под знаком. Но самое главное – уметь понять, что это число, какое имеет значение и как его использовать в решении задачи.
Для того чтобы прочитать корень, необходимо быть внимательным и учесть несколько факторов:
1
Знак корня – важно определить, является ли корень положительным или отрицательным;. 2
Показатель степени – определяет степень, в которую следует возвести корень;
2. Показатель степени – определяет степень, в которую следует возвести корень;
3. Число под знаком извлечения – определяет, какое число нужно извлечь из под корня.
Если учесть эти факторы, то можно легко и правильно прочитать корень и использовать его в решении задачи. Например, корень из числа 25 с показателем степени 2 будет равен 5, так как 5*5=25.
В таблице ниже приведены примеры чтения различных корней:
| Корень | Правило чтения |
|---|---|
| √4 | Корень из числа 4 равен 2 |
| ∛8 | Кубический корень из числа 8 равен 2 |
| ∜16 | Четвертый корень из числа 16 равен 2 |
Используя правила чтения корней и знание их определения, можно более эффективно и точно работать с числами в математике.
Значение маленькой цифры для обозначения степени корня
Маленькая цифра, которая располагается перед корнем сверху, называется показателем степени корня. Её значение определяет, в какую степень нужно возвести корень, чтобы получить исходное число.
Например, если у нас есть корень второй степени, обозначаемый символом √2, то мы должны возвести число в степень 2 для получения исходного числа. То есть, если √2 равно 4, это значит, что число 4 нужно возвести в квадрат, чтобы получить число 2.
Аналогично, для корня третьей степени, обозначаемого символом √3, мы должны возвести число в степень 3, чтобы получить исходное число. Если √3 равно 27, это означает, что число 27 нужно возвести в куб, чтобы получить число 3.
Важно помнить, что маленькая цифра перед корнем отличается от показателя степени, который может быть записан после знака равенства. Маленькая цифра перед корнем указывает, в какую степень нужно возвести корень, чтобы получить исходное число, в то время как показатель степени после знака равенства указывает на саму степень корня
Использование маленькой цифры перед корнем позволяет нам более чётко указывать, какую степень корня мы имеем в виду и что именно она означает.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
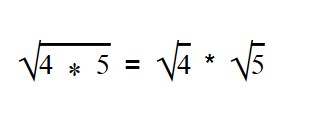
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
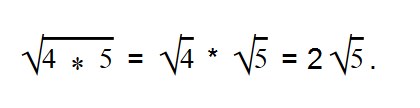
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
- √28
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня. -
Ответ: по правилу извлечения квадратного корня из произведения,
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами. - Вынесите множитель из-под знака корня в выражении: √24
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4. - Упростите выражение:
Вынесем в двух последних выражения множитель из-под знака корня.
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:
Далее вычисляем все, что в скобках:
Почему нужны два определения?
Внимательный читатель уже наверняка заметил, что все квадратные корни, приведённые в примерах, извлекаются из положительных чисел. Ну, в крайнем случае из нуля. А вот кубические корни невозмутимо извлекаются абсолютно из любого числа — хоть положительного, хоть отрицательного.
Почему так происходит? Взгляните на график функции $y={{x}^{2}}$:
 График квадратичной функции даёт два корня: положительный и отрицательный
График квадратичной функции даёт два корня: положительный и отрицательный
Попробуем с помощью этого графика посчитать $\sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку
\
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
\
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y, т.е. не принимает отрицательных значений.
Подобная проблема возникает у всех корней с чётным показателем:
- Строго говоря, корней с чётным показателем $n$ у каждого положительного числа будет сразу две штуки;
- Из отрицательных чисел корень с чётным $n$ вообще не извлекается.
Именно поэтому в определении корня чётной степени $n$ специально оговаривается, что ответ должен быть неотрицательным числом. Так мы избавляемся от неоднозначности.
Зато для нечётных $n$ такой проблемы нет. Чтобы убедиться в этом, давайте взглянем на график функции $y={{x}^{3}}$:
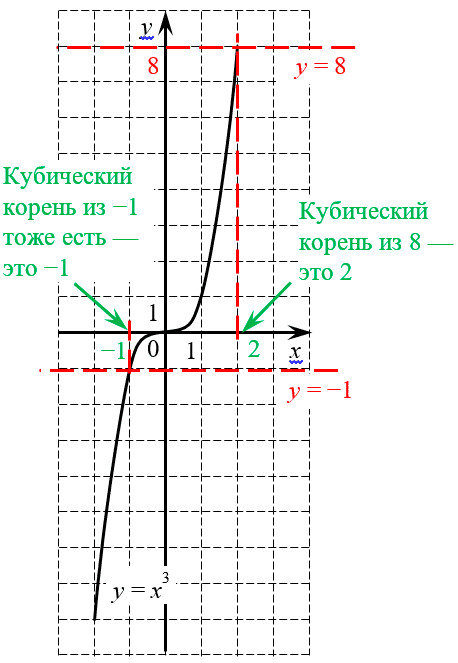 Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Из этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Число перед корнем как стилистическое средство
В русском языке число перед корнем может указывать на количество, интенсивность или степень каких-либо качеств
Оно позволяет усилить выразительность слова и обратить на себя внимание слушателя или читателя
Например, слово «трикратный» становится более эмоционально окрашенным и сильным, чем обычное слово «кратный». Число «три» перед корнем придает ему значение «трехкратный», подчеркивая интенсивность.
Также, число перед корнем может использоваться для создания ритмической и мелодичной структуры фразы или стихотворения. Оно добавляет музыкальности и гармоничности в речь.
Более того, число перед корнем может использоваться в качестве метафорического или символического способа передачи информации. Например, число «сто» перед корнем может олицетворять большое количество чего-либо, а число «тысяча» — еще большее число. Такие слова вносят дополнительные оттенки смысла в текст и вызывают живое восприятие.
Важно отметить, что использование числа перед корнем требует аккуратности и соблюдения стилистической меры. Чрезмерное использование этого средства может привести к банальности или преувеличению смысла. Поэтому важно учитывать контекст и цель речи при его использовании
Поэтому важно учитывать контекст и цель речи при его использовании. В итоге, число перед корнем является важным стилистическим средством, позволяющим усилить эмоциональную нагрузку, создать ритмичность и мелодичность, а также добавить дополнительные оттенки смысла в слово или фразу
В итоге, число перед корнем является важным стилистическим средством, позволяющим усилить эмоциональную нагрузку, создать ритмичность и мелодичность, а также добавить дополнительные оттенки смысла в слово или фразу.
Что такое корень в математике
Корень n-степени из определенного числа x характеризуется в качестве определенной величины y, то есть \(y^{n}=x\). В данном уравнении n является натуральной величиной, которая носит название степень корня (показатель, именно на эту величину необходимо совершать возведение в степень). Обычно величина степени корня эквивалентна 2 или же является величиной, что больше 2. Вариант, при котором n=1 не интересен для математического сообщества, результат не изменится.
Такой вариант написания часто используется в алгебре: \(y=\sqrt{x}\). Обозначение в виде корневого знака \(\sqrt{}\) носит название радикала. Величина x является подкоренной величиной. Обычно данное число является либо комплексным, либо вещественным. Также возможно внесение под корень более сложных алгебраических явлений, например матриц, вычетов, операторов и других.
Вот такие математические действия можно совершать с величинами, которые являются корнями:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
- умножение;
- деление;
- возведение в степень.
Основные особенности корней:
- Только положительная величина, которая точно определена, способна быть корнем нечетной степени, рассчитанным из положительного значения: \(\sqrt{x}=y\), где \(x,y>0\), показатель n является нечетным значением. Приведем пример: \(\sqrt{125}=5, \sqrt{32}=2, \sqrt{1}=1\).
- Только отрицательная величина, которая точно определена, способна стать корнем нечетной степени, рассчитанным из отрицательного значения: \(\sqrt{x}=y\), где x,y<0, показатель n является нечетным значением. Приведем пример: \(\sqrt{-8}=-2\), \(\sqrt{-243}=-3\), \(\sqrt{-1}=-1\).
- Две величины с двумя разными знаками получится, если рассчитывать корень четной степени из величины без отрицательного знака. Оба полученных значения несмотря на то, что будут разные по своему знаку, но будут эквиваленты по собственному модулю. \(\pm{\sqrt{x}}=\pm{y},\) где \(x,y>0\), показатель n является четным значением. Приведем пример: \(\pm{\sqrt{4}}=\pm{2}\).
- Невозможно извлечь корень из числа со знаком «минус» четной степени — такой величины просто нет в сфере вещественных величин, потому что в процессе возведения каждого вещественного значения в степень четной величины итогом можно считать только число без знака «минус». Но корни подобного типа возможно вычленять, но в системе, которая намного шире обычный корневой — множестве комплексных чисел. В таком случае величины корня будут являться комплексными значениями. \(\sqrt{x}\) нельзя найти в сфере вещественных значений при условии x<0, показатель n является четным.
- Стоит запомнить, что при вычислении корня всех натуральных степеней из нуля будет все равно ноль. \(\sqrt{0}\).
Число перед корнем: практическое применение
Число, стоящее перед математическим корнем, имеет особое значение и приносит существенные практические преимущества в различных областях науки и техники.
Одним из примеров практического применения числа перед корнем является вычисление сферических координат. В системе координат, где есть географическая широта и долгота, часто применяется формула, в которой число перед корнем обозначает радиус Земли и позволяет точно определить расстояние между двумя точками на поверхности Земли.
В другом примере, число перед корнем используется в определении взвешенной суммы
В задачах, где нужно учесть важность каждого компонента, вес каждого члена суммы может быть выражен числом перед корнем, что помогает качественно учесть значимость каждого фактора
Также, число перед корнем находит широкое применение в физике и инженерии, например, в расчете сопротивления материалов. В формулах, описывающих связь между нагрузкой и деформацией, число перед корнем часто определяет геометрические свойства объекта и позволяет рассчитать необходимые параметры конструкции.
- В системах электропитания число перед корнем используется для определения эффективного напряжения в периодических сигналах, таких как переменный ток в электрических сетях.
- В экономических моделях, число перед корнем может описывать непропорциональность зависимости цены от объема потребления или производства.
- Психологические исследования используют число перед корнем для описания ненормальных распределений в данных или отклонений от среднего значения.
Таким образом, число перед корнем имеет практическое применение в различных научных и технических областях и помогает решать сложные задачи, требующие точности и учета различных факторов.





























