Альтернативные определения и интерпретации пи минус альфа

Выражение «пи минус альфа» имеет несколько альтернативных определений и интерпретаций в различных математических и физических контекстах.
| Определение | Интерпретация |
|---|---|
| 1 | В математике, «пи минус альфа» может означать разность между числом пи (π) и углом альфа (α). В этом случае, результат является числом и может использоваться в различных геометрических и тригонометрических вычислениях. |
| 2 | В физике, «пи минус альфа» может означать разность между физической величиной, связанной с числом пи, и другой физической величиной, связанной с углом альфа. В этом случае, результат может иметь физическую интерпретацию и использоваться в различных физических уравнениях и моделях. |
| 3 | В различных областях, «пи минус альфа» может использоваться в символическом смысле, чтобы указать на обратное или противоположное значение или действие по отношению к числу пи или углу альфа. |
В зависимости от контекста использования и области применения, значение и интерпретация выражения «пи минус альфа» может меняться и иметь различные математические и физические значения.
Альфа в задачах на подобие фигур

Альфа в геометрии представляет собой отношение длины стороны одной фигуры к длине соответствующей стороны другой подобной фигуры. Оно обозначается греческой буквой «α» (альфа).
Задачи на подобие фигур часто требуют вычисления пропорций и использования альфа. Рассмотрим примеры:
- Даны два треугольника. Известно, что их стороны подобные. Найдите длину стороны второго треугольника, если известна длина соответствующей стороны первого треугольника и альфа.
- Ребро куба подобно отрезку длиной 5 см. Найдите длину ребра параллелепипеда, подобного этому кубу, если альфа равно 3.
- Длина стороны большего треугольника равна 20 см, а альфа равно 1,5. Найдите длину стороны меньшего треугольника.
Решение задач на подобие фигур сводится к применению формулы:
Длина стороны фигуры 2 = Длина стороны фигуры 1 * α
где α — альфа, отношение длины соответствующих сторон.
Таким образом, подставляя известные значения в формулу, можно найти неизвестную величину.
| Задача | Формула | Решение |
|---|---|---|
| 1 | Длина стороны 2 = Длина стороны 1 * α | Длина стороны 2 = Длина стороны 1 * α |
| 2 | Длина ребра 2 = Длина ребра 1 * α | Длина ребра 2 = 5 см * 3 = 15 см |
| 3 | Длина стороны 2 = Длина стороны 1 * α | Длина стороны 2 = 20 см * 1,5 = 30 см |
Таким образом, альфа является важным понятием в задачах на подобие фигур, позволяющим вычислять длину неизвестной стороны, основываясь на известных пропорциях и отношении.
Роль пи минус альфа в технических и инженерных областях

Понятие пи минус альфа имеет важное значение в различных технических и инженерных областях. Пи минус альфа представляет собой разность между числовым значением пи и углом альфа
В аэродинамике пи минус альфа используется для расчета и анализа динамического поведения летательного аппарата. Это понятие играет особую роль при определении аэродинамических характеристик, таких как аэродинамическое подъемное сопротивление и момент вокруг продольной оси. Значение пи минус альфа позволяет инженерам прогнозировать и оптимизировать работу летательных аппаратов в различных условиях полета.
Во многих областях инженерии, таких как механика, электротехника и тепловые науки, пи минус альфа используется для моделирования и анализа систем. Знание данной величины позволяет инженерам предсказывать и управлять поведением системы в различных условиях. Например, в механике пи минус альфа может быть использовано для определения траектории движения объекта или расчета сил, действующих на него.
Также в области сигнальной обработки и телекоммуникаций пи минус альфа играет важную роль. Оно может использоваться для компенсации и коррекции искажений сигналов при передаче данных. Знание значения пи минус альфа позволяет инженерам проводить точную обработку сигналов и повышать качество передачи информации.
Итак, пи минус альфа имеет большое значение в различных технических и инженерных областях, где оно используется для моделирования, анализа и оптимизации систем. Понимание этого понятия позволяет инженерам разрабатывать и улучшать технологии, повышать эффективность работы систем и обеспечивать высокое качество продукции и услуг.
Повседневные примеры числа пи
Большинство из нас знает, что ? — это иррациональное число, начинающееся с 3,14, но знаете ли вы, что оно обладает некоторыми удивительными свойствами? Пи символизирует отношение длины окружности круга к его диаметру, что означает, что это важная математическая константа, которую вы можете видеть в нашей повседневной жизни.
- Измерение кругов: есть ты раньше играл с хулахупами? Отношение длины окружности кольца к его диаметру всегда равно ?. Таким образом, если диаметр кольца составляет 3 фута, его длина окружности составляет 3? футов, что составляет около 9,42 фута.
- Архитектура: от колонн до куполов и арок число пи имеет решающее значение. строительные конструкции, которым нужны круглые формы. Без ? было бы невозможно рассчитать правильные углы и размеры, которые делают эти конструкции прочными и безопасными.
- Кулинария: Вы любите печь пироги? В процессе используется круг, а ? используется для измерения окружности корочки пирога. Пи также используется для измерения ингредиентов круглых десертов, требующих точности.
Свойства числа ? изучались на протяжении веков, и математики продолжают работать с этим числом, чтобы раскрыть новые секреты. Одно из самых интересных свойств числа ? состоит в том, что оно никогда не заканчивается, а его цифры не следуют никакой закономерности. Это означает, что если вы возьмете цифры числа пи и поместите их в таблицу, они будут случайными.
| цифры числа пи | значение |
|---|---|
| 3 | . |
| 1415 | 9265 |
| 3589 | 7932 |
Несмотря на кажущуюся случайность числа пи, оно лежит в основе законов физики и Вселенная
Важность этого числа нельзя отрицать. От вычисления диаметра круга до исследования глубочайших областей космоса число Пи может раскрыть бесчисленное количество тайн
Празднования и традиции Дня числа числа Пи
Каждый год 14 марта люди во всем мире отмечают День числа Пи, чтя математическую константу пи (?). Пи — это отношение длины окружности любого круга к его диаметру, число, которое никогда не заканчивается и никогда не повторяется.
Первое празднование Дня числа Пи состоялось в научном музее Exploratorium в Сан-Франциско в 1988 году. С тех пор , День числа Пи стал неофициальным праздником для любителей математики во всем мире, с различными традициями и празднованиями.
- Есть пирог. Одна из самых популярных традиций Дня числа числа Пи — есть пирог, чтобы отпраздновать это событие. Это может быть яблочный, вишневый, тыквенный или любой другой пирог, главное, чтобы он был круглым, как математическая константа пи.
- Соревнования по чтению числа Пи: некоторые любители математики бросают вызов себе и другим, чтобы запомнить как можно больше цифр. число пи, как они могут, и проводить конкурсы на чтение в День числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа числа число числа числа число числа число числа число пи, а также викторины.
Число 7 имеет особое значение в числе Пи. Это первое простое число, которое встречается в десятичной записи числа пи после запятой. На самом деле первые шесть цифр числа пи (3,14159) не содержат числа 7.
| Десятичные разряды числа пи | Первое появление 7 | Позиция 7 |
|---|---|---|
| 10 | 7 | 4-й знак после запятой |
| 100 | 7 | 16-й знак после запятой |
| 1000 | 7 td> | 17-й знак после запятой |
Это интересное явление привело ко многим математическим гипотезам и теориям, в том числе к знаменитой «гипотезе о семи». Гипотеза гласит, что если вы присвоите числовое значение буквам английского алфавита (A=1, B=2, C=3 и т. д.), сумма букв в семи степенях числа пи (?, ??, ?? , … ??) делится на 7.
День числа Пи — это не только праздник математики и чисел, но и праздник интеллектуального любопытства и исследований. Это напоминает нам ценить тайны Вселенной и продолжать искать знания и понимание.
Related Articles
- Calculate mean, median, mode, variance, standard deviation in Python
- Matrix operations with NumPy in Python
- Power and logarithmic functions in Python (exp, log, log10, log2)
- Complex numbers in Python
- NumPy: Trigonometric functions (sin, cos, tan, arcsin, arccos, arctan)
- Fractions (rational numbers) in Python
- Set operations in Python (union, intersection, symmetric difference, etc.)
- Find GCD and LCM in Python (math.gcd(), lcm())
- pandas: Cumulative calculations (cumsum, cumprod, cummax, cummin)
- NumPy: np.sign(), np.signbit(), np.copysign()
- Get the filename, directory, extension from a path string in Python
- Load, parse, serialize JSON files and strings in Python
- Get/set the recursion limit in Python (sys.getrecursionlimit, sys.setrecursionlimit)
- The pass statement in Python
- Check OpenCV Build Information: getBuildInformation()
Число пи в культуре и искусстве
Число пи — уникальный математический константный коэффициент, который используется в различных сферах жизни, включая науку, инженерию, архитектуру, астрономию и даже искусство.
Некоторые художники используют число пи при создании своих произведений искусства для достижения определенной искусственной симметричности и гармонии, которые не могут быть достигнуты без использования этого символа математики.
В архитектуре число пи используется для создания красивых и надежных строений, таких как мосты, здания и купола. В культуре и искусстве число пи может быть выражено в разных формах, например, в геометрических узорах, в шрифтах и в музыкальных композициях.
Большинство известных музыкальных композиций имеют факторы, связанные с числом пи
Некоторые из них включают в себя длительность нот, темп и тональность.
В геометрических узорах использование числа пи важно для создания более сложных и красивых узоров, которые привлекают внимание зрителя.
Номер 8: Шриниваса Рамануджан
Шриниваса Рамануджан был индийским математиком, чьи работы имели решающее значение для развития теории чисел. Он независимо открыл множество математических теорем, и его статьи сыграли важную роль в развитии области математики. Одним из его наиболее заметных вкладов в число пи была его формула для его бесконечного ряда.
| Формула | Обозначение |
|---|---|
| 1/pi = (2*sqrt(2))/9801 * SUM(k=0,inf)(4k)!( 1103+26390k)/(k!) ^4 | Ряд для 1/pi |
Эта формула позволяет вычислять число «пи» с чрезвычайно большим количеством знаков после запятой. С помощью этой формулы Рамануджан и другие математики смогли вычислить число пи с точностью более 17 миллионов знаков после запятой.
Кроме того, Рамануджан обнаружил много других удивительных и интересных свойств числа пи. Он продемонстрировал, что это иррациональное число, а это означает, что его нельзя выразить как отношение двух целых чисел. Он также обнаружил, что непрерывная дробь числа пи, выражение числа пи в виде бесконечной последовательности дробей, имеет удивительные закономерности, которые можно использовать для вычисления его значения.
Вклад Шринивасы Рамануджана в область математики, особенно что касается числа пи, сделали его легендарной фигурой в мире науки и вывели Индию на передний план математических исследований.
История и происхождение числа Пи
Пи – это математическая константа, представляющая отношение длины окружности к ее диаметру. Это одно из самых важных и известных математических понятий, и его значение изучалось на протяжении тысячелетий. Символом числа пи является греческая буква ?, и это иррациональное число, которое продолжается бесконечно, не повторяясь.
- Самое раннее известное вычисление числа пи было сделано древним вавилонским математиком около 2000 г. до н.э. Они обнаружили, что число пи равно 3,125.
- Первое точное приближение числа пи было сделано греческим математиком Архимедом в 3 веке до нашей эры. Он использовал метод, называемый «описанием и вписыванием», когда он рисовал многоугольники вокруг и внутри круга, чтобы оценить его окружность и диаметр.
- Символ ? впервые был использован для обозначения этого отношения валлийским математиком Уильямом Джонсом в 1706 г., а позже он был популяризирован швейцарским математиком Леонардом Эйлером в 18 веке.
На протяжении веков многие математики внесли свой вклад в изучение числа пи, в том числе китайские, индийские и персидские. ученые. Первая десятичная аппроксимация числа пи была вычислена английским математиком Уильямом Броункером в 1655 году, а затем уточнена многими другими.
Сегодня число пи является фундаментальной константой в математике и естественных науках и встречается в бесчисленных уравнения и формулы. Его значение было вычислено с помощью компьютеров до триллионов знаков после запятой, и оно продолжает очаровывать и бросать вызов математикам по всему миру.
| Год | Значение числа Пи | Метод расчета |
|---|---|---|
| 2000 г. до н.э. | 3,125 | Неизвестно |
| 3 век до н.э. | 3.1418 | Метод Архимеда |
| 1655 | 3.1415927 | Метод Броункера |
| 2021 | 3.141592653589793238 | Компьютерный расчет |
Несмотря на долгую историю числа пи, об этом загадочном и увлекательном числе еще многое предстоит узнать. От своего древнего происхождения до современных расчетов число Пи продолжает вызывать любопытство и удивление у людей всех возрастов и слоев общества.
Формулы отрицательных углов
Что такое отрицательный угол и как с ним работать? На самом деле, все просто: чтобы получить отрицательный угол, достаточно поставить перед аргументом минус. Например, sin(-x).
Применять такой угол при решении выражений с тригонометрическими функциями очень неудобно, поэтому от минуса обычно избавляются. Однако делать это нужно по правилам: нельзя просто его не написать.
Чтобы правильно избавиться от минуса, нужно понимать, что отрицательные углы напрямую связаны с графиками тригонометрических функций, а именно с четностью функций. Подробнее про четность функции можно прочесть в статье «Определение и график функции».
Четность функции можно сравнить со снежинкой. Если мы посмотрим на нее под микроскопом и мысленно проведем ось посередине, то окажется, что левая и правая части одинаковые. Единственное их отличие – они отзеркалены.
Также и четные функции: справа и слева они имеют одинаковые отзеркаленные части.

Четная функция – функция, для которой выполняется равенство \(f(x)=f(-x)\).
Повторим, такие функции симметричны относительно оси ординат. Можно представить, что вместо оси у у нас стоит зеркало, в которой график функции отражается.
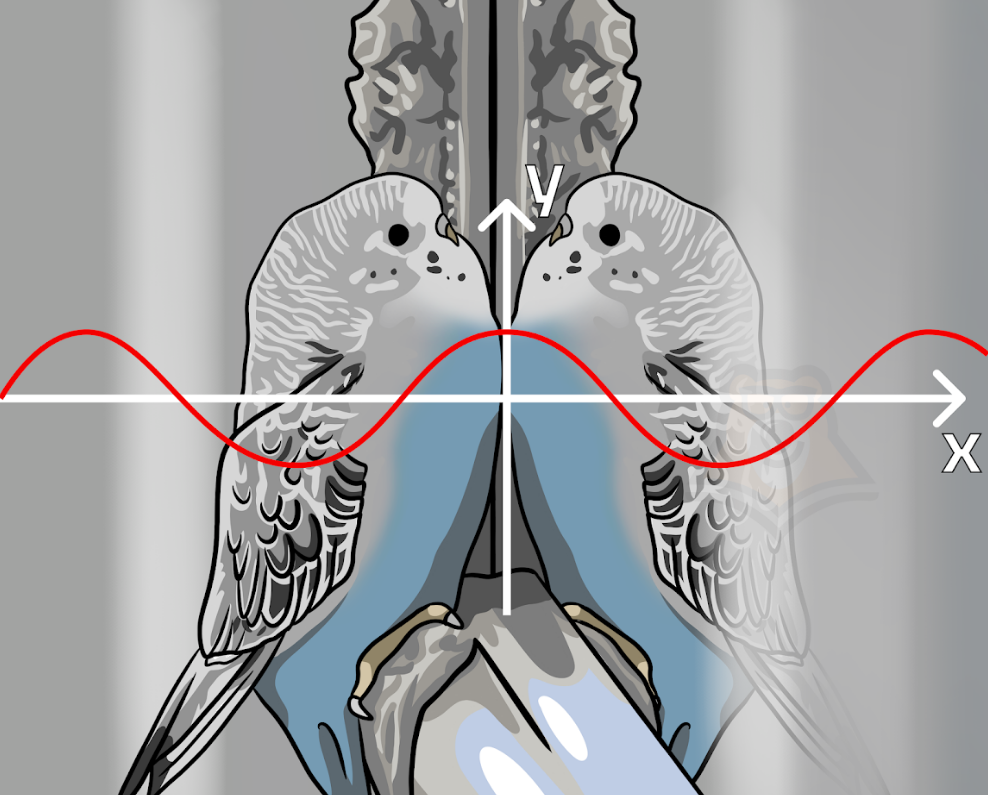
Если мы вспомним графики тригонометрических функций и проверим их симметричность, то заметим, что четным является только косинус. Этим он выделяется среди других функций.

Синус, тангенс и котангенс – нечетные функции. Для них будет справедливо уравнение \(f(-x)=-f(x)\). Их графики не симметричны относительно оси у.
Таким образом, опираясь на четность функции, мы можем вывести четыре формулы:
\(cos(-x)=cos x\)\(sin(-x)=-sin x\)\(tg(-x)=-tg x\)\(ctg(-x)=-ctg x\)
Пользуясь этими формулами, можно легко избавляться от минуса в аргументах функции.
Итак, мы попробовали изменить аргумент с помощью минуса. А если попробовать поставить перед аргументом коэффициент, например, 2?
История открытия числа пи
Число пи – это одна из фундаментальных математических констант, которая описывает соотношение длины окружности к ее диаметру. Интерес к этой константе существовал с древнейших времен и различные цивилизации пытались найти способ ее вычисления.
Древнейшее документальное упоминание о числе пи относится к древнему Вавилону и датируется приблизительно 1900 годом до н.э. В этом документе указывается, что длина окружности равна трехдвадцати произведениям диаметра.
В Древнем Египте число пи было приблизительно равно 3,16, а в Древнем Китае – 3,14. В Европе в Средние века, число пи было вычислено арабским математиком Аль-Хорезми до пятидесяти знаков после запятой.
Современный символ числа пи был введен в 1706 году английским математиком Уильямом Джонсом. В 1761 году швейцарский математик Йоганн Ламберт доказал, что число пи является иррациональным, а значит, его точное значение не может быть записано в виде дроби. В 1882 году немецкий математик Фердинанд фон Линдеманн доказал теорему, что число пи – алгебраический трансцендентный число, что означает, что оно является корнем алгебраического уравнения, но не может быть выражено в виде алгебраической дроби с целыми коэффициентами.
- 1901 год – наибольшее число пи, которое было вычислено на счетных машинах
- 1949 год – первое вычисление числа пи с использованием ЭВМ
- 2019 год – число пи было вычислено до 31,4 триллионов знаков после запятой
Пи минус альфа в физике и естественных науках

В физике, «пи» обычно обозначается как математическая константа, равная приблизительно 3,14159. Число пи широко используется в различных формулах и уравнениях, связанных с геометрией, тригонометрией и другими областями физики.
Альфа (α), с другой стороны, обычно используется для обозначения угла. В контексте углов, альфа обычно представляет собой угол, находящийся в диапазоне от 0 до 180 градусов.
Таким образом, «пи минус альфа» обозначает разность между числом пи и углом альфа. Эта разность может быть выражена в градусах или радианах, в зависимости от системы измерения, используемой в конкретном контексте.
Пи минус альфа находит свое применение в различных научных дисциплинах, включая физику, математику, астрономию и другие. Оно может быть включено в уравнения, модели и формулы для описания различных физических явлений и процессов.
Важно отметить, что значение пи минус альфа будет зависеть от конкретного значения угла альфа. При значениях альфа, равных 0 или 180 градусов, «пи минус альфа» примет значение пи
В остальных случаях значение «пи минус альфа» будет меньше значения пи.
Фактчек
Чтобы решать сложные тригонометрические уравнения и неравенства, необходимо уметь преобразовывать выражения. Для этого нужно правильно пользоваться формулами.
Условно, формулы можно разделить на несколько групп: основные формулы тригонометрии, формулы отрицательных углов, формулы двойных углов, формулы сложения и вычитания углов, формулы понижения степени, формулы для суммы, разности и произведения синусов и косинусов.
К основным тригонометрическим формулам в первую очередь относится основное тригонометрическое тождество: \(sin^2x + cos^2x = 1\)
Оно и еще несколько других формул раскрывают связь между функциями.
Важно запомнить, что формулы работают в обе стороны: их можно читать справа налево и слева направо. Более того, многие формулы можно выводить друг из друга, что значительно упрощает их заучивание.
Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.
Для решения тригонометрических уравнений необходимо применять аркфункции, то есть функции, обратные тригонометрическим
С помощью аркфункций мы находим угол через значение тригонометрической функции.
Окружность и его характеристики
Главные характеристики окружности:
1. Радиус — это расстояние от центра окружности до любой ее точки. Обозначается буквой «r».
2. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр равен удвоенному значению радиуса. Обозначается буквой «d».
3. Окружность состоит из бесконечного числа дуг, которые являются частью ее окружности. Дуга — это отрезок окружности между двумя точками на ней.
4. Длина окружности — это периметр окружности. Обозначается буквой «C». Длина окружности можно вычислить по формуле C = 2πr, где «π» — это математическая постоянная, приближенное значение которой равно 3,14.
5. Площадь окружности — это площадь ограниченная ее границей. Обозначается буквой «S». Площадь окружности можно вычислить по формуле S = πr^2.
Минус пи на окружности представляет собой геометрическую точку, которая находится на окружности и соответствует угловой мере минус пи радиан (–π рад).
Символы вероятности и статистики
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ⋂ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ⋂ B ) = 0,5 |
| P ( A ⋃ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ⋃ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( x макс + x мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Исторический контекст понятия пи минус альфа
Понятие «пи минус альфа» имеет свои истоки в истории математики и физики. Оно было введено в научный оборот в конце XIX века и с тех пор нашло свое применение в различных областях науки и техники.
Первоначально понятие пи (π) возникло в древней Греции. Древние греки долго пытались найти отношение длины окружности к ее диаметру. Они проводили различные измерения и приходили к приближенным значениям этого соотношения. В результате этих исследований было получено число π, которое является иррациональной и трансцендентной константой. Оно равно примерно 3,14159.
Понятие альфа (α) в свою очередь имеет глубокие корни в греческом алфавите. Буква альфа была принята для обозначения различных величин, в том числе и углов.
Сочетание пи минус альфа используется для описания смещения угла относительно значения π. Это позволяет точнее описывать угловые величины и избежать округлений при использовании обычной меры угла в радианах.
Понятие пи минус альфа нашло применение в различных областях науки, таких как физика, математика, инженерия и другие. Оно позволяет более точно определять угловые величины и использовать их в различных вычислениях и измерениях.
Что символизирует число «пи»? Часто задаваемые вопросы
2. Почему пи иррациональное число?
Пи является иррациональным числом, потому что его нельзя представить в виде дроби, и его десятичное представление никогда не повторяется.
4
Почему число пи важно в математике и естественных науках?. Пи используется в широком спектре математических и научных приложений, от расчета площади и объема круга до моделирования поведения волн и систем в физике и технике
Пи используется в широком спектре математических и научных приложений, от расчета площади и объема круга до моделирования поведения волн и систем в физике и технике.
5 . Кто первым открыл число Пи?
Концепция числа «пи» существует уже тысячи лет, но греческий математик Архимед был первым, кто точно оценил его значение около 200 г. до н.э.
Special functions¶
- math.erf(x)
-
Return the error function at
x.The function can be used to compute traditional statistical
functions such as the cumulative standard normal distribution:def phi(x): 'Cumulative distribution function for the standard normal distribution' return (1.0 + erf(x sqrt(2.0))) 2.0Added in version 3.2.
- math.erfc(x)
-
Return the complementary error function at x. The complementary error
function is defined as
. It is used for large values of x where a subtraction
from one would cause a loss of significance.Added in version 3.2.
- math.gamma(x)
-
Return the Gamma function at
x.Added in version 3.2.
Какие результаты можно достичь, используя пи пополам?
Метод пи пополам – это численный метод для приближенного вычисления значения числа π. Используя этот метод, можно достичь точности вычисления π с заданной погрешностью.
Главное преимущество метода пи пополам заключается в его простоте и эффективности. Он основан на принципе разбиения задачи на более простые части и последовательном уточнении результатов. Применяя этот метод, можно достичь высокой точности вычисления π при помощи простых вычислений и небольших объемов памяти.
Вычисление числа π с использованием метода пи пополам может быть полезно во многих областях науки и техники. Например, точное значение π необходимо при решении задач в физике, математике, компьютерной графике, алгоритмах и многих других областях. Кроме того, значение π играет важную роль во многих формулах и уравнениях, и его точное вычисление может улучшить результаты вычислений и моделирования.
Метод пи пополам может быть использован для вычисления π с любой заданной точностью. Чем больше итераций метода будет выполнено, тем более точное значение π можно получить. Но при этом стоит учитывать, что каждая итерация требует определенных ресурсов, включая вычислительное время и память. Поэтому необходимо балансировать точность вычислений и доступные ресурсы.
При применении метода пи пополам можно использовать различные алгоритмы для уточнения результата и оптимизации вычислений. Например, можно использовать алгоритм Булдож или метод Риттера. Также можно распараллеливать вычисления для ускорения процесса и повышения эффективности метода.
В итоге, используя метод пи пополам, можно достичь высокой точности вычисления числа π, что позволяет улучшить результаты во многих областях науки и техники. Этот метод является одним из простых и эффективных численных методов для приближенного вычисления значения π.
























