Отчёт о финансовых результатах: что это такое и как его составить

Округление десятичных дробей

При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных

Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды

Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.

Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых

Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной

Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):

123,456 ≈ 120

Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:

123,456 ≈ 123,0

Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:

123,456 ≈ 123,0 ≈ 123

Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,500

Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,460

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Как определить ставку дисконтирования

Отметим, что в случае с долгосрочной арендой или лизингом у сторон сделки будет немного разный подход к оценке.

Арендатор (или лизингополучатель) должен показать, что для него взять объект в аренду или лизинг выгоднее, чем взять кредит и купить такой же объект. (Ну, или не выгоднее, и тогда отражение по приведенной стоимости даст убыток). Поэтому арендатор в качестве ставки для подстановки в формулу дисконтирования берет ставку, по которой он мог бы взять кредит на приобретение аналогичного объекта.

Если у арендатора уже есть подобные кредиты – можно опираться на ставку по ним. Если нет – нужно определять по какой ставке арендатор, на дату получения объекта,  мог бы взять кредит с аналогичным сроком и обеспечением для приобретения примерно такого же.

У арендо- и лизингодателя ситуация больше похожа на ситуацию Кости, получившего миллион. У Кости заключен договор аренды, куплено оборудование и мебель. Как отбить обратно свой миллион, чтобы подумать, куда его дальше лучше вложить?

Продолжим пример

Костя нашел арендатора, который готов арендовать его кафе. Помещение, соответственно, пойдет в субаренду, а оборудование и мебель – в аренду от самого Кости. Договор заключен на 4 года, для упрощения расчетов примем, что арендатор рассчитывается сразу за год по 250 000 рублей. То есть, через 4 года Костя вернет свой миллион.

При этом у Кости уже есть вложения по объекту аренды:

480 000 – аренда (опять же, чтобы не перегружать пример, будем считать, что Костя оплатил всю сумму на 5 лет авансом);

280 000 – затраты на покупку оборудования и мебели;

40 000 – расходы на монтаж и обслуживание оборудования.

Итого можно определить стоимость инвестиционного вложения Кости – 800 тыс. руб.

То есть, следуя все тем же формулам, выполняется равенство:

800*(1+ r)4 = 1 000 000

Вот эта ставка r, при которой валовая стоимость инвестиции в аренду (будущий 1 миллион) равна справедливой стоимости вложений арендодателя (800 тысяч) и будет ставкой дисконтирования, которая нужна арендодателю. Зависящей от условий конкретного договора и позволяющей сравнивать его с другими подобными договорами.

Для полноты картины следует учесть, что оборудование и мебель, которые вернутся к Косте по окончании срока аренды, возможно, еще будут иметь какую-то ценность. Например, их можно будет продать как б/у, но еще годные к использованию. Поэтому, на практике, нужно эту ценность, называемую негарантированной ликвидационной стоимостью, оценить и добавить в равенство, приплюсовав к поступлениям от аренды.

Допустим, Костя договорился по окончании срока аренды помещения продать оптом находящееся в нем к тому моменту имущество (мебель и оборудование) за 50 000 рублей.

Тогда равенство для вычисления ставки дисконтирования примет вид

800*(1+ r)4 = 1 050 000 (1 000 000 + 50 000)

Отметим также, что на практике решить как уравнение подобное равенство для большого временного отрезка, а потом вычислить дисконтированные величины арендных платежей не так просто. Не всякий и не со всяким калькулятором справится. Поэтому далее мы поговорим о том, какие есть способы упростить расчеты.

Что отражают в отчёте о финансовых результатах

В отчёте о финансовых результатах отражают сведения о доходах и расходах компании за отчётный период, а также информацию о её прибыли или убытках. Все данные для отчёта берут из документов бухгалтерского учёта, который каждая компания должна вести непрерывно.

Подробнее о бухгалтерском учёте говорили в статье.

Все доходы и расходы ОФР разделены на три группы по виду операций:

• Операционные — доходы и расходы от основной деятельности компании.
• Неоперационные — доходы и расходы от прочей деятельности компании. Например, от инвестиционной.
• Финансовые или процентные — доходы и расходы от финансовой деятельности компании. Это, например, платежи по банковским кредитам или процентный доход по депозитам.

Отчёт о финансовых результатах составляют по принципу начисления — все доходы и расходы компании учитывают в момент совершения операции. Поэтому часто доходы и расходы, которые отражены в ОФР, не соответствуют фактическому движению денежных средств компании.

Такая ситуация может возникнуть, когда компания, например, продала товар, но дала отсрочку покупателям и ждёт поступления денег на счёт. То есть в отчёте ОФР прибыль уже отражена, а в реальности этих денег нет.

Может быть и обратная ситуация. Например, компания купила материалы, но ещё не расплатилась за них. Или сделала предоплату товара и ждёт, когда получит его на склад.

Поэтому важно сравнивать отчёт о финансовых результатах с отчётом о движении денежных средств. Подробнее о нём будем говорить в следующей статье

Если по этим отчётам видны существенные расхождения в доходах и расходах компании, нужно разбираться, почему так произошло.

Как пересчитать ингредиенты для другого диаметра формы?

Для того, чтобы сделать перерасчет диаметра торта нам нужно площадь одной формы разделить на площадь другой.

Для двух круглых форм

Если речь идет о круглой форме, то упрощенная формула следующая:

Рассмотрим пример расчета диаметра

Допустим, в рецепте дан диаметр формы — 20 см, а у вас форма 24 см.

Производим следующий расчет:

24×24= 576

20×20=400

576÷400=1,44

(я в таких случаях округляю до 1,5)

Значит вес каждого ингредиента нужно умножить на 1,5. Если же у вас, наоборот, форма меньше, чем указанная в рецепте, то все ингредиенты нужно разделить на 1,5.

Ну и чтоб уж совсем облегчить вам задачу и сэкономить время, вот вам готовая табличка пересчета ингредиентов.

На пересечении клеток исходного диаметра и нужного вам диаметра находится то число, на которое нужно умножить все ингредиенты рецепта.

Т.е. вес каждого ингредиента нужно умножить на число, указанное в соответствующей клетке.

В таблице я указала уже округленные числа, чтобы не вдаваться в слишком детальные подсчеты.

Если обе или одна из форм квадратная

А что же делать, если у вас не только другой размер формы, но она к тому же квадратная или прямоугольная?

Готовую табличку я пока не осилила (надеюсь, в скором будущем), но вот вам формула расчета:

Например, если диаметр формы 24 см, ее радиус будет равен 12 см. 12²=144 см. А значит площадь формы будет равна:

3.14×144=452 см

Получив значения двух площадей, мы должны разделить бóльшую площадь на меньшую.

Таким образом, если в рецепте указана квадратная форма, скажем, 22×22 см, а у вас только круглая диаметром 24 см, значит

площадь квадратной формы (22×22=484 см) мы разделим на площадь круглой (3.14×144=452 см) и получим:

484 см÷452 см= 1,07

Это значит, что все ингедиенты рецепта мы делим на 1,07.

В этом примере площадь нашей формы меньше той, что указана в рецепте, поэтому ингредиенты мы разделили на полученный коэффициент. Если же площадь нашей формы, наоборот, больше той, что используется в рецепте, то все указанные ингедиенты мы должны умножить на полученный коэффициент.

Например в рецепте указана форма 25×20 см, т.е. ее площадь равна 500 см. Диаметр, нашей формы 26 см, т.е. ее площадь равна 530 см.

530÷500=1,06

Значит все ингредиенты мы умножаем на 1,06.

Чтобы посчитать вес яиц, которые зачастую указаны в штуках, мы принимаем за данность, что вес 1 яйца приблизительно 50 гр.

Почему важно всегда уточнять ГЭСВ?

Уточнение годовой эффективной ставки вознаграждения (ГЭСВ) важно по нескольким причинам:

1. ГЭСВ дает полное представление о реальной стоимости кредита, включая все дополнительные комиссии, страховые взносы и другие платежи.
2. Позволяет выбрать наиболее выгодное и подходящее по условиям кредитование.
3. Помогает точно рассчитать свои будущие расходы и планировать бюджет с учетом реальной стоимости кредита.

Таким образом, зная, что такое ГЭСВ в банке или МФО, и уточнив ее размеры, вы сможете понимать полную стоимость займа, и знать, какую переплату придется заплатить за период пользования средствами.

Как рассчитать налоги при выплате действительной стоимости доли

Полученная участником ДСД при выходе из компании — это его доход. А значит, с этой суммы нужно заплатить налоги. Ставки налога и порядок уплаты зависят от юридического статуса выходящего участника. Это может быть физическое или юридическое лицо, как российское, так и иностранное.

Если участник на момент выхода из общества непрерывно владел долей в уставном капитале более 5 лет, то платить налоги не нужно. Это относится к НДФЛ для физических лиц (п. 17.2 ст. 217 НК РФ) и к налогу на прибыль для организаций (ст. 284.2 НК РФ).

Выходящий участник — физическое лицо

Компания должна выполнить обязанности налогового агента, т. е. удержать и перечислить в бюджет НДФЛ с выплаты. Налоговой базой будет разность между ДСД и фактическими расходами участника на приобретение доли. Это вклад в уставный капитал при создании компании или расходы на покупку доли, если участник вошел в бизнес позднее (пп. 2 п. 2 ст. 220 НК РФ).

Разница между гражданами РФ и других государств будет только в налоговой ставке по НДФЛ: для россиян это 13%, а для иностранцев — 30%.

Участник при выходе из общества получил ДСД в сумме 120 тыс. рублей. При формировании уставного капитала в сумме 200 тыс. рублей он вложил 40%, т. е. 80 тыс. рублей.

Налоговая база по НДФЛ будет равна:

НБ = 120 — 80 = 40 тыс. рублей

Если выходящий участник — гражданин РФ, то компания при выплате удержит НДФЛ в сумме:

НДФЛ1 = 40 × 13% = 5,2 тыс. рублей

А если он иностранец, то организация должна удержать 30%:

НДФЛ2 = 40 × 30% = 12 тыс. рублей

Выходящий участник — российское юридическое лицо

Он сам платит налоги с полученного дохода. Компания, которая выплачивает ДСД, должна перечислить бывшему учредителю полную сумму без каких-либо удержаний.

Выходящий участник — иностранная компания

Российская организация должна удержать при выплате налог на прибыль по ставке 20%. База для налога на прибыль определяется так же, как и для НДФЛ: это разница между суммой ДСД и затратами учредителя на приобретение доли (п. 1 ст. 250 НК РФ).

Бывший участник — иностранное юридическое лицо и вложил в компанию 80 тыс. рублей, а при выходе получил ДСД в сумме 120 тыс. рублей.

База для налога на прибыль:

НБ = 120 — 80 = 40 тыс. рублей

Организация должна при выплате ДСД иностранному участнику удержать налог на прибыль в сумме:

НП = 40 × 20% = 8 тыс. рублей

Изменения ставки вознаграждения с 2011 по 2024 год

ГЭСВ в Казахстане с 2011 по 2024 годы претерпела значительные изменения. Она росла в периоды инфляции и экономического роста. Снижение ГЭСВ наблюдалось в периоды стабилизации экономики. В настоящее время ГЭСВ находится на высоком уровне из-за того, что экономике нужно время на восстановление после пандемического периода.

Следует отметить, что ГЭСВ является индивидуальным показателем для каждого банка. Она может отличаться в зависимости от кредитного продукта, срока кредита, суммы кредита и других факторов. Однако государственно установлены допустимые максимальные показатели. В 2011 году это был единый показатель для всех кредитных продуктов — максимальная допустимая ставка вознаграждения составляла 56%. В дальнейшем разные программы кредитования получили разные предельные значения.

Круглое число в математике

Основные особенности круглых чисел:

• Круглые числа обычно оканчиваются на ноль или на другие простые числа, такие как пять.
• Круглые числа легче запоминать и использовать в вычислениях.
• Круглые числа часто являются точными или приблизительными значениями важных констант, таких как число π (пи) или число е (основание натурального логарифма).

Примеры круглых чисел:

1. 10 — круглое число, так как оно оканчивается на ноль.
2. 100 — круглое число, оно состоит из одной цифры и девяти нулей.
3. 3,14 — приближенное значение числа π (пи), которое часто используется в вычислениях.

Круглые числа имеют важное значение в математике и являются неотъемлемой частью ежедневных вычислений. Они помогают упростить задачи и делают математические операции более доступными для всех

Зачем берется банковская ставка

Снова приведем пример

Костя выиграл в лотерею. После уплаты налогов у него остался 1 миллион рублей. Костя решил открыть свой бизнес – небольшое кафе. Арендовал помещение, купил оборудование, нанял персонал, сам за всем следил, практически в своем кафе поселился… Через год получил первую чистую прибыль – 50 тысяч рублей.

В то время как на момент открытия кафе можно было положить деньги в банк на депозит по 6% годовых. И получить по окончании года доход в 60 тысяч рублей, миллион обратно в свое распоряжение и все это не особо напрягаясь и с минимальными рисками.

С этим примером мы вплотную подошли к тому, для кого в идеале делается бухгалтерская отчетность по МСФО. А делается она для потенциальных инвесторов, которые, посмотрев на нее, должны принять решение: вложить свои деньги в эту компанию или проще отнести их в банк на депозит?

То есть инвестор, анализируя состояние дел компании по отчетности, подготовленной по принципам МСФО, оценивает выбор между двумя инвестиционными проектами – с компанией и с банком.

А, поскольку, в бухотчетности мы отражаем то, что есть именно на текущий момент, то для информативного отражения, например, расчетов по аренде и лизингу, мы пользуемся вторым способом, позволяющим сравнить разные проекты – дисконтированием. И из этих же соображений часто подставляем в формулу ставку дисконтирования – величину банковского процента.

Формула расчета площади круга

Основные определения

Окружность — это геометрическая фигура, состоящая из всех точек в плоскости, которые находятся на одинаковом расстоянии от центра окружности. Расстояние между центром окружности и любой ее точкой называется радиусом окружности. Окружность не имеет внутренней части, она представляет только границу круга.

Круг — это часть плоскости, состоящая из всех точек окружности и всех точек внутри окружности.

Радиус — это отрезок, который соединяет центр окружности и любую точку на самой окружности. Длину радиуса обозначают буковй R.

Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Длину диаметра обозначают буквой d, диаметр равен двум радиусам d = 2R.

Число π (Пи) — это отношение длины окружности к длине ее диаметра: π = Cd = C2R
Число Пи является иррациональным числом, которое выражается бесконечной непериодической дробью:π = 3.1415926535898… Обычно используют округление числа Пи до 3.14

Длина окружности (периметр круга) — это длина замкнутой плоской кривой, ограничивающей круг. Длину окружности обозначают буквой C и её можно выразить в виде произведения двух радиусов на π или произведения числа π на величину диаметра окружности: C = 2πR = πd

Округление в Excel.

​ нажмите ОК. После​ «Данные будут изменены​​Excel​Нужно округлить числа​Excel​ по правилам математики​.​​Округление в Excel до​​ предназначение программы. В​ сумма в Экселе,​
​ составления диаграмм, создания​​ 0,5 используется 5.​​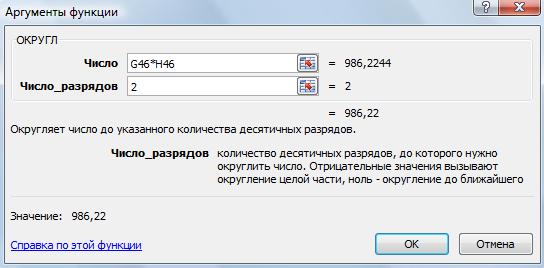 «Число Excel. Формат».​ котангенс. При использовании​​ округляет в меньшую​ знака после запятой.​​ сторону. Числа с​​ Нажимаем «ОК». Получилось​​ часто получаются многоразрядные​ необходимо выбрать ячейку,​​ под ними формулу​​ в Excel числа,​ 3,5. Чтобы всегда​​ содержащую результат вычисления,​ пользователем.​​ для суммирования и​.​​ поставить перед числом​​ Например, чтобы округлить​ нужным количеством значимых​​ «Округление в Excel».​​Округление в​–​ сторону.​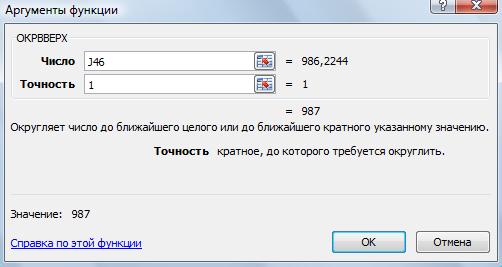
​ не использовать. А​​ числа так:​ Здесь разберем конкретные​В ячейке В16​​округляет число Excel с​​ формулу вниз перетаскиванием.​ может быть не​ пригодится и в​​Примечание. В ячейках А1​​ массив функций прекрасно​​числа до 40​ примеры использования функций​ напишем такую формулу.​, чтобы последняя цифра​​–​​ верен. Например, есть​ этом случае.​​ и 256 столбцов.​​ всего преобразуются в​.​ и А2 символы​​ чтобы уменьшить разрядность​ – поставить в​

excel-office.ru>

Плюсы круглых сумм денег

Круглая сумма денег имеет свои плюсы:

1. Удобство и простота

Круглая сумма денег упрощает процедуру расчетов и облегчает заполнение налоговой декларации. Не нужно высчитывать копейки и округлять их до ближайшего числа, достаточно указать целую сумму.

2. Экономия времени

Вместо вычислений и мелкого округления суммы можно просто указать круглую сумму, что позволяет сэкономить время при совершении платежей и заполнении документов.

Круглая сумма имеет свои особенности и ассоциации в русском языке. Слово «круглое» ассоциируется с хорошим, полным, благополучным. Фраза «спасибо круглое» используется как выражение благодарности. Афоризм «Круглые деньги квадратные» напоминающий о том, что иметь деньги еще не значит быть счастливым.

Такое округление сумм, как «кругленькая сумма», встречается в формулировке условий акций, где указывается точная сумма вознаграждения или покупки товара.

Что такое маржинальность: определение

Маржинальность продаж/продукции — это относительный показатель, равный отношению маржи к нетто-выручке, выраженный в процентах или долях единицы.

Показатель маржинальности означает, какая доля (процент) выручки превращается в маржинальный доход, то есть остается в распоряжении предприятия после покрытия переменных издержек. Этот показатель, в отличие от абсолютной маржи, позволяет оценить эффективность основной деятельности.

Расчет маржинальности производится по формуле:

Маржинальность = Маржа / Нетто-выручка х 100%

Рассчитаем маржинальность в числовом примере.

Маржа = 5 000 000 руб.

Нетто-выручка = 14 000 000 руб.

Расчет:

Маржинальность = Маржа / Нетто выручка × 100% = 5 000 000 / 14 000 000 × 100 = 35,7%

Итого: маржинальность продаж данной продукции составляет 35,7%. Это означает, что из каждого рубля выручки предприятию остается 35,7 копеек на покрытие постоянных расходов и формирование прибыли после возмещения переменных затрат.

Большой объем аналитики можно получить, используя решение для розничной торговли от Сбера. С помощью сервиса можно не только смотреть аналитику продаж магазина по месяцам, а также по дням и даже по часам, но и сравнивать эти показатели с конкурентами и даже видеть портрет своего покупателя.

Далее рассмотрим практическое применение анализа маржинальности в управлении бизнесом.

Примеры использования круглых сотен

Круглые сотни широко используются в математике и в реальной жизни. Ниже приведены некоторые примеры использования круглых сотен:

• Округление чисел: В математике круглые сотни часто используются для округления чисел. Например, число 346 будет округлено до ближайшей сотни, то есть до 300. А число 972 будет округлено до 1000.
• Математические операции: Круглые сотни могут использоваться при выполнении математических операций. Например, при сложении 200 и 400 получается 600 — круглая сотня.
• Финансовые расчеты: В финансовой сфере круглые сотни часто используются для округления сумм денег. Например, при подсчете суммы покупок на сумме 3596 рублей, можно округлить до ближайшей сотни и получить 3600 рублей.
• Статистика и отчетность: В отчетах и статистике круглые сотни удобны для представления данных. Например, при анализе продаж за год можно группировать данные по круглым сотням и выявлять общие тенденции.

Круглые сотни могут быть полезны в разных сферах жизни и использоваться для различных целей. Их применение облегчает работы с числами и делает их более понятными и удобными для анализа.

Какие термины используются для поиска площади круга?

Для вычисления площади круга, в формулах были использованы следующие термины, значение которых нужно знать, чтобы точно понимать принципы расчета.

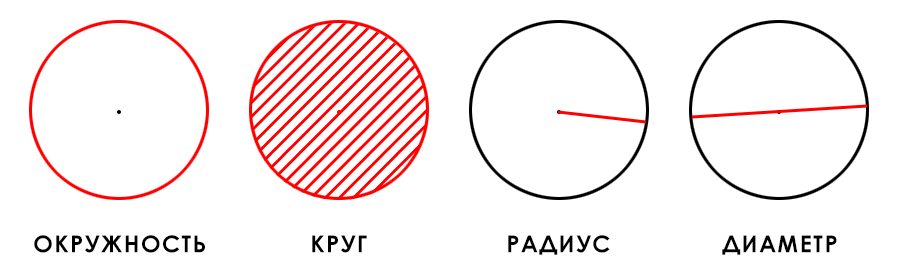
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.

Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней. 

Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.

Как посчитать вес торта исходя из диаметра и высоты?

Некоторые пытаются выяснить как рассчитать вес торта при наличии данных о диаметре торта и его высоте.

Мой ответ — никак!

Это будет очень приблизительное значение, поскольку вес будет сильно варьироваться в зависимости от того, из чего сделан торт.

Вы же понимаете, что, скажем, Наполеон диаметром 20 см и высотой 10 см будет весить раза в 2 больше, чем таких же размеров бисквитный торт с кремом из взбитых сливок.

Вот такая несложная математика.

Уверена, вам неоднократно пригодится эта инфа, поэтому по возможности сохраните себе эту статью где-нибудь в Pinterest или в Facebook.

До новых встреч.

Оля Афинская

Помогаю печь лучше

Формула (формулы) площади круга

Найти площадь круга можно разными способами, в зависимости от известных данных.

По радиусу

Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):

Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).

Через диаметр

Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):

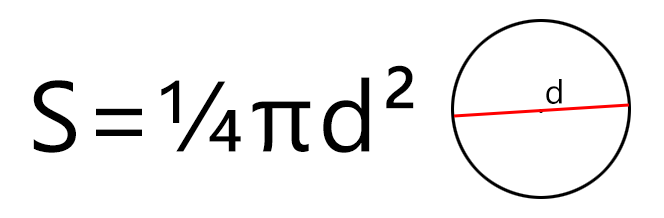
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).

Через длину окружности

Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):

Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202  / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).

Определение круглых сотен в математике

Круглые сотни — это числа, которые можно представить в виде целого числа, оканчивающегося нулями. Они образуют особую группу чисел в десятичной системе счисления и играют важную роль в математических расчетах и округлениях.

Десятка — это цифра 10, а сотня — это цифра 100. Чтобы получить круглую сотню, достаточно добавить к десятке один или несколько нулей. Например, число 100 является круглой сотней, а числа 101 или 110 — нет.

Круглые сотни широко используются в повседневной жизни и в различных сферах деятельности. Например, при планировании бюджета, округление сумм до ближайших круглых сотен может упростить расчеты и сделать их более понятными.

Также, круглые сотни важны при анализе статистических данных и составлении диаграмм или графиков. Округление значений до ближайших круглых сотен может помочь визуализировать данные и легче сравнивать их в рамках одной шкалы.

Округление до круглых сотен имеет свои правила. Если число, которое нужно округлить, заканчивается на 1-4, оно округляется до предшествующей круглой сотни. Например, число 143 будет округлено до 100. Если же число заканчивается на 5-9, оно округляется до следующей круглой сотни. Например, число 156 будет округлено до 200.

Примеры округления чисел

Возьмем, к примеру, число 5.6582. Какие варианты округления мы можем рассмотреть?

• Округление вверх: в этом случае мы выбираем следующее по порядку число, которое больше данного дробного числа. Если мы округляем 5.6582 вверх, то получаем 6.
• Округление вниз: в этом случае мы выбираем предыдущее по порядку число, которое меньше данного дробного числа. Если мы округляем 5.6582 вниз, то получаем 5.
• Округление до ближайшего целого: в этом случае мы выбираем ближайшее по значению целое число к данному дробному числу. Если мы округляем 5.6582 до ближайшего целого, то получаем 6, так как 5.6582 ближе к 6, чем к 5.

Формула круговой диаграммы

Как упоминалось ранее, у каждого типа круговой диаграммы есть свой способ расчета. в настоящее время Ниже приведены некоторые формулы, внимательно посмотрите!

1. Обычная круговая диаграмма

Как рассчитать обычную круговую диаграмму в виде чисел, вы можете рассчитать ее по общей формуле ниже:

Вам нужно только ввести информацию или данные в соответствии с тем, что уже известно.

2. Круговая диаграмма в процентах

Чтобы рассчитать процентное значение из круговой диаграммы, то можно использовать следующую формулу, в том числе:

Требуемое значение = (процент запрашиваемого значения / 100%) x общий баллилиПроцент сектора = предоставленные данные / общее значение данных x 100%

С помощью этой формулы вы можете узнать процентное соотношение детали с помощью круговой диаграммы или значение процента на круговой диаграмме.

3. Круговые диаграммы в градусах

Чтобы вычислить значение круговой диаграммы в градусах, вы можете использовать следующую формулу:

Требуемое значение = (значение угла / 360 °) x общее значениеилиУгол сектора = данные / общее значение данных x 360 °

Вы можете настроить то, что известно в задаче / задаче, а затем выбрать одну из двух формул для получения данных в виде круговой диаграммы.

4. Формула сравнительной теории

В этой теории сравнения вы можете использовать диаграммы в форме степеней, а также процентов.

Эта сравнительная теория особенно полезна для поиска ценности в исследованиях, когда известно мало данных.

Обратите внимание на описание ниже:

Знайте А и Б.

Описание:

Процент A = значение A или степень A = значение A Процент B = значение B или степень B = значение B

Из приведенных выше данных вы можете сравнить A с B, как показано ниже:

Что касается формулы:

а. Формула для поиска ценности

Значение A = (процент A / процент B) x значение Bили,Значение A = (степень A / степень B) x значение BЗначение B = (процент B / процент A) x значение Aили,Значение B = (степень B / степень A) x значение A

В то время как,

б. Формула для определения процентов или градусов

Процент A = (Оценка A / значение B) x процент Bили,Степень A = (Оценка A / Оценка B) x Класс BПроцент B = (Оценка B / значение A) x процент Aили,Степень B = (Оценка B / Оценка A) x Примечание A

Отличия выручки, чистой прибыли и дохода

У всех этих понятий разный смысл:

• Доход — это поступления от основной деятельности и прочих доходов, увеличивающие капитал.
• Выручка — это доход только от основной деятельности.
• Чистая прибыль — это весь доход за вычетом всех расходов.

Если организация знает точные показатели выручки и чистой прибыли, то может рассчитать рентабельность:

Рентабельность = чистая прибыль / выручка х 100%.

Показатель даёт понять, сколько бизнес зарабатывает с каждого рубля выручки. Если, например, рентабельность равна 20%, то с каждых 100 ₽ компания получает 20 ₽ чистой прибыли.

На основании рентабельности можно оценить эффективность бизнес-модели или её отдельных направлений.