Как измерить изгибающий момент
- Метод статического тестирования: Этот метод включает применение известной силы или момента к объекту и измерение прогиба или искривления. По прогибу или искривлению можно определить значение изгибающего момента с использованием соответствующих формул и моделей.
- Метод деформационных датчиков: Этот метод использует специальные датчики, которые регистрируют деформацию объекта под действием нагрузки. Деформация может быть прямо связана с изгибающим моментом, и поэтому измерение деформации позволяет определить значение момента.
- Метод гибких полостей: Этот метод базируется на использовании гибких полостей, таких как трубки или камеры, которые заполняются жидкостью или газом. Приложение изгибающего момента вызывает изменение давления в полостях, которое можно измерить и использовать для определения момента.
Выбор метода измерения изгибающего момента зависит от конкретных условий и требований тестирования. Каждый метод имеет свои преимущества и ограничения, и может быть более или менее подходящим для определенного приложения.
Примеры изгибающего момента
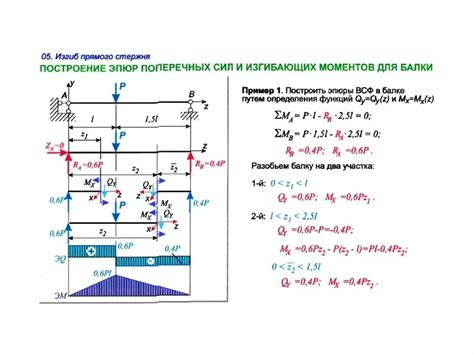
Изгибающий момент возникает в различных ситуациях, где имеется загибаемая или изгибаемая конструкция. Вот несколько примеров, когда изгибающий момент играет важную роль:
| Пример | Описание |
| 1 |
Балка в здании. Когда строится здание, каркас состоит из различных балок, которые несут нагрузку. В процессе эксплуатации строения на балки могут действовать различные нагрузки, такие как вес перекрытий, мебели и людей. В результате возникает изгибающий момент, который деформирует балку. Это пример изгибающего момента в работе. |
| 2 |
Вал в двигателе автомобиля. В двигателе автомобиля имеется вал, который крутится при работе двигателя. В процессе вращения вал испытывает силы изгиба, особенно в тех местах, где он имеет выступы или подшипники. Эти силы создают изгибающий момент, который должен быть учтен при проектировании вала, чтобы избежать его деформации или поломки. |
| 3 |
Рама велосипеда. Велосипедная рама является основным элементом конструкции велосипеда. Она должна быть достаточно жесткой, чтобы выдерживать силы, которые могут возникать во время катания. Однако при преодолении неровностей или при сильных ударах по раме, она может быть подвержена изгибающим моментам, которые приводят к ее деформации или повреждению. |
Понятие изгиба в технической механике
Изгиб – это механическое деформирование объекта, при котором происходит изгибание или искривление его формы. Изгиб может происходить под воздействием внешних сил или моментов, которые приложены к объекту.
Изгиб является одним из основных типов нагружений, с которыми сталкиваются инженеры и конструкторы при проектировании и расчете различных конструкций и деталей.
Основные понятия, связанные с изгибом:
- Изгибающий момент (М) – момент, который вызывает наклон или изгиб объекта. Изгибающий момент может быть постоянным или изменяться в зависимости от условий нагрузки.
- Изгибающий момент огибающей (Мо) – наибольший изгибающий момент, который возникает в объекте.
- Изгибающий момент среднего слоя (Мср) – момент, который возникает в среднем слое объекта при изгибе. Величина изгибающего момента среднего слоя может быть меньше или больше изгибающего момента огибающей.
Примеры конструкций, подверженных изгибу:
- Балки – длинные прямоугольные или круглые элементы, которые поддерживаются на обоих концах и испытывают изгибающие нагрузки. Балки широко используются в строительстве и машиностроении.
- Пластины – плоские элементы, которые могут быть прямоугольной, круглой или иной формы. Пластины могут изгибаться под воздействием внешних нагрузок.
- Арки – криволинейные конструкции, которые подвержены изгибу при приложении внешнего нагрузки. Арки используются в архитектуре и строительстве.
Изучение изгиба в технической механике позволяет инженерам и конструкторам правильно расчитывать и учитывать прочность и деформируемость различных конструкций и деталей, чтобы они могли выдерживать необходимые нагрузки и служить в течение длительного времени.
Инженерное применение изгиба
Изгиб — одно из наиболее распространенных явлений в технической механике и имеет огромное инженерное применение. Изгиб позволяет создавать прочные и устойчивые конструкции, обладающие необходимой гибкостью и приспособленные для различных нагрузок.
Примеры инженерного применения изгиба можно найти во многих отраслях промышленности:
- Строительство мостов и сооружений. Изгиб применяется для создания прочных и устойчивых конструкций, способных выдерживать огромные нагрузки, такие как грузовики и поезда.
- Авиастроение. Изгиб используется для создания крыльев самолетов, которые должны быть достаточно гибкими, чтобы адаптироваться к изменению аэродинамических сил во время полета.
- Автомобильная промышленность. Изгиб применяется при проектировании кузовов автомобилей, чтобы обеспечить им необходимую прочность и безопасность.
- Судостроение. Изгиб используется для создания корпусов судов, которые должны быть достаточно гибкими, чтобы справиться с внешними нагрузками, такими как волны и течения.
Изгиб также играет важную роль в разработке различных механизмов, таких как пружины, амортизаторы и различные виды подвесок.
Все эти примеры демонстрируют значимость изгиба в инженерном дизайне и его важное место в технической механике. Понимание свойств и поведения материалов при изгибе позволяет инженерам создавать более прочные, безопасные и эффективные конструкции, которые могут выдерживать различные виды нагрузок
Эпюры для двухопорных балок
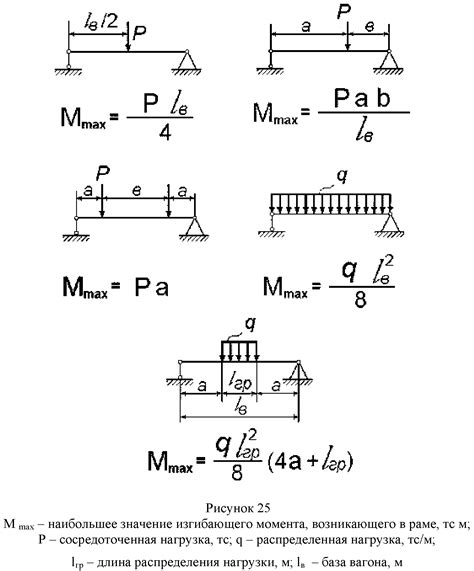
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),
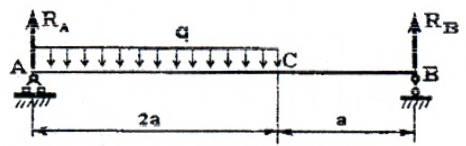
необходимо вначале найти опорные реакции и только потом строить эпюры.
Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑MA=0 и ∑MB=0.
Записываем уравнения и находим значения реакций:
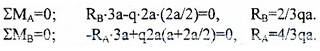 YС
YС
Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).
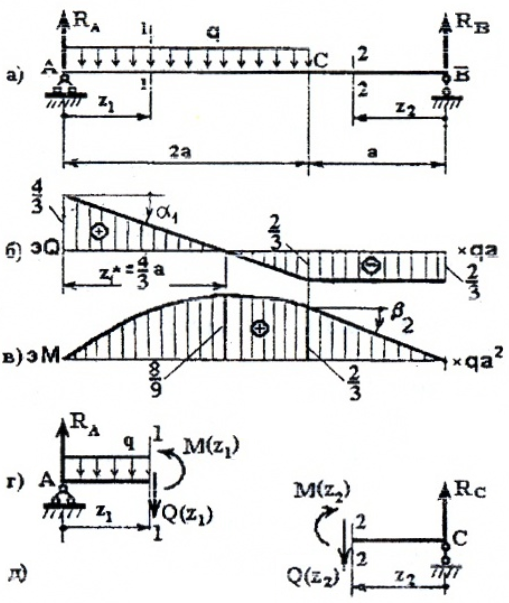
I участок (AC): 0 ≥ z1 ≥2a (рис. 6, а, г) Q(z1)=RA-qz1 — прямая, которую строим по двум граничным точкам:
1A111A11
II силовой участок: 0 ≥ z2 ≥ a.
1
Уважаемые студенты! На нашем сайте можно получить помощь по техническим и другим предметам: Решение задач Выполнение учебных работ Помощь на экзаменах
Пример определения поперечной силы и изгибающего момента
Давайте посмотрим, так сказать, воочию на эти внутренние силовые факторы. Рассмотрим балку, закрепленную с левого торца жесткой связью и нагруженной с другого торца силой P.
Воспользуемся любимым методом сечений. Рассечем балку в произвольном сечении на расстоянии x1 от свободного торца балки.
Заменим действие одной части балки на другую внутренними силовыми факторами, так сказать уравновесим обе части балки.
Если записать уравнения статики для одной из частей, например, для правой части балки, то получим:
∑Mc= P·x1-M=0. Тогда M= P·x1, то есть изгибающий момент в исследуемом сечении будет равен произведению внешней силы на расстояние от свободного торца до сечения.
Теперь рассмотрим балку подверженную только чистому изгибу. На свободном торце балки приложим только момент силы.
В поперечных сечениях, как говорилось выше, будут возникать только изгибающие моменты и только одной величины. Не трудно догадаться, что внутренний изгибающий момент будет равен внешнему моменту.
Важно научиться строить правильно эпюры изгибающих моментов и поперечных сил. Перед тем как читать статью про построение эпюр, рекомендую сначала ознакомиться с правилом знаков
Изгибающий момент в строительстве
Изгибающий момент возникает тогда, когда на элемент действует внешняя сила, создающая изгиб. В строительстве такие силы часто возникают под воздействием собственного веса конструкции, воздушных нагрузок, тепловых деформаций и других факторов. Изгибающий момент стремится изменить форму элемента, вызывая его изгиб.
Примером изгибающего момента в строительстве может послужить балка или бетонное перекрытие. Под воздействием нагрузки, например, распределенной нагрузки от нахождения людей или предметов, балка начинает изгибаться. Изгибающий момент в этом случае вызывает появление напряжений в материале балки, которые должны быть учтены при проектировании конструкции, чтобы она оставалась прочной и безопасной.
Таким образом, изгибающий момент играет важную роль в строительстве, определяя прочность и устойчивость сооружений. Он учитывается при разработке проектов, выборе материалов и конструировании элементов, чтобы обеспечить долговечность и безопасность строительных конструкций.
Примеры изгибаемых конструкций
Изгибаемые конструкции широко применяются в различных областях техники и строительства. Ниже приведены некоторые примеры изгибаемых конструкций.
1. Балки
Балки — это типичный пример изгибаемых конструкций. Они используются в строительстве для поддержки нагрузок на большие расстояния. Например, балки могут использоваться в крышах зданий или в мостах.
2. Перекрытия
Перекрытия — еще один пример изгибаемых конструкций, используемых в строительстве. Они служат для поддержки вертикальной нагрузки, например, от этажей здания. Перекрытия могут быть выполнены из железобетона, дерева или металла.
3. Арки
Арки — это конструкции, которые подвергаются изгибу под действием нагрузки. Они используются в архитектуре для создания красивых и прочных строений, таких как соборы, амфитеатры и мосты.
4. Рессоры
Рессоры — это изгибаемые конструкции, используемые в автомобильной промышленности для амортизации ударов и вибраций. Они обычно изготавливаются из пружинной стали и подвергаются изгибу при движении транспортного средства.
5. Стойки
Стойки — это вертикальные изгибаемые конструкции, используемые в различных областях, таких как строительство и машиностроение. Они служат для поддержки вертикальной нагрузки или для установки других элементов конструкции.
6. Трубопроводы
Трубопроводы — это изгибаемые конструкции, используемые для транспортировки жидкостей или газов. Они могут быть изготовлены из различных материалов, включая металл, пластик или композиты, и могут иметь различные формы и диаметры.
7. Листы и пластины
Листы и пластины — это плоские изгибаемые конструкции, широко используемые в машиностроении и строительстве. Они могут быть изготовлены из различных материалов, таких как металл, пластик или стекло, и использоваться для создания различных деталей и оболочек.
Чистый и поперечный изгиб балки
Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.
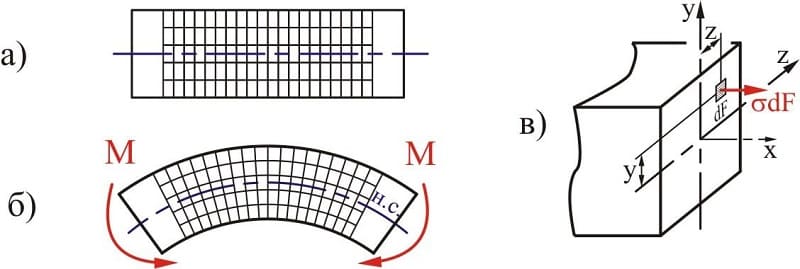
При изгибе балки вводят следующие допущения:
- Во всех сечениях присутствуют только нормальные напряжения.
- Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
- Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
- При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.
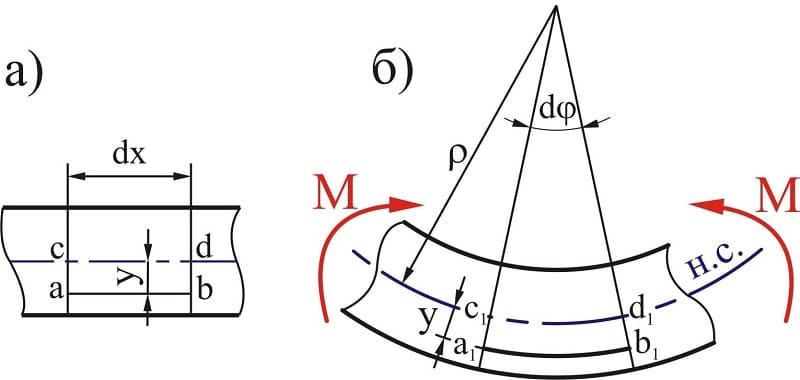
Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.
Что такое изгибающий момент?
Изгибающий момент обычно возникает в прямоугольных и круглых сечениях стержней, балок, дуг и других конструкций под действием внешних сил. Например, приложение силы к концу балки может вызвать изгибающий момент, который приведет к искривлению балки вокруг определенной оси.
Изгибающий момент измеряется в ньютонах-метрах (Н·м) или килоньютонах-метрах (кН·м) в системе СИ. Он может быть положительным или отрицательным, в зависимости от направления силы и ориентации изгиба. Положительный момент вызывает сжатие на одной стороне объекта и растяжение на другой стороне, тогда как отрицательный момент приводит к обратным эффектам.
Изгибающий момент является важным показателем при проектировании и анализе различных конструкций, таких как мосты, здания, автомобили и самолеты. Понимание изгибающего момента позволяет инженерам предсказывать и оценивать, насколько прочными и устойчивыми будут эти конструкции.
Примером изгибающего момента может служить прогиб деревянной доски, когда на нее накладывается внешняя сила. Деревянная доска начинает изгибаться, подвергаясь действию изгибающего момента.
iSopromat.ru
Внутренние поперечная сила и изгибающий момент возникают в поперечных сечениях балки при её изгибе под действием внешних нагрузок.
Поперечным изгибом называется такой вид деформирования бруса, при котором внешние нагрузки действуют перпендикулярно к его продольной оси. Деформация изгиба заключается в искривлении оси бруса.
Брус с прямой осью, работающий на изгиб, называется балкой. Если плоскость действия внешних нагрузок проходит через ось балки и одну из главных центральных осей поперечного сечения, изгиб называется прямым. В этом случае ось балки искривляется в плоскости действия нагрузок и является плоской кривой.
В сечениях балки возникают два внутренних силовых фактора: изгибающий момент Мх и поперечная сила Qy
Дифференциальные зависимости между q, Qy и Мх имеют вид:
Изгиб называется чистым, если в сечении балки возникает только изгибающий момент Мх.
Уважаемые студенты! На нашем сайте можно получить помощь по техническим и другим предметам: Решение задач Выполнение учебных работ Помощь на экзаменах
В этой статье будем говорить как определяется поперечная сила и изгибающий момент. Оба эти внутренних силовых фактора появляются при поперечном изгибе. При чистом изгибе, когда на конструкцию действует только моменты, в поперечных сечениях появляются только изгибающие моменты.
Изгибающий момент действует в плоскости перпендикулярной к поперечному сечению и совпадает с одной из главных центральных осей.
Поперечная сила действует в плоскости поперечного сечения.
Расчёты на прочность при изгибе
Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом
Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.
Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.
Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:
- дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
- способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
- семейство принятых гипотез;
- разработанные правила построения графических изображений (построение эпюр).
https://youtube.com/watch?v=EI-hmVm8rbQ
Расчёт параметров производится в три этапа:
- при проверочном расчёте (вычисляют величину максимального напряжения);
- на этапе проектирования (производится выбор толщины и параметров сечения бруса);
- во время вычисления допустимой нагрузки.
Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.
Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей.
При чистом изгибе эпюры имеют следующие особенности:
- на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
- на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
- в точке появления приложенного момента, скачок равен величине этого параметра;
- на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
- в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).
На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:
- расчёт производят с учётом нормальных напряжений;
- в качестве основного предположения принимают гипотезу о плоских сечениях;
- продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
- деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
- для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
- физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
- процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).
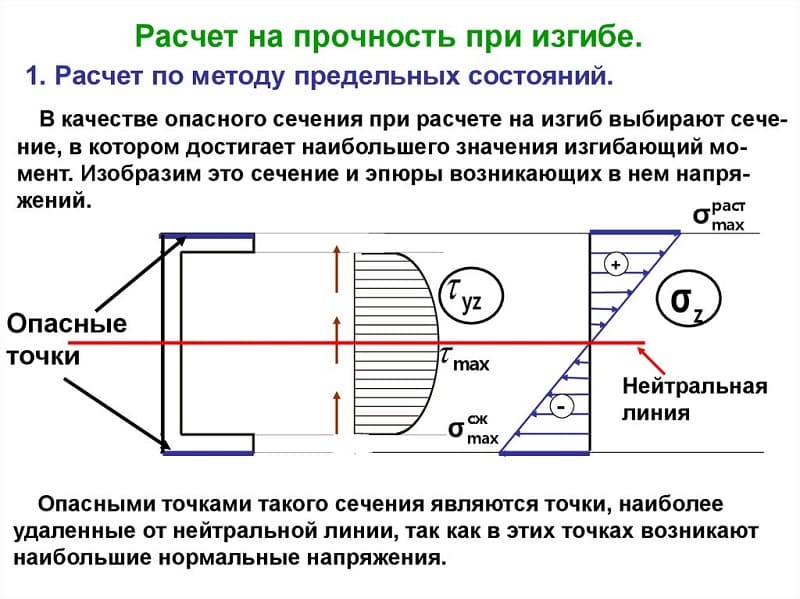
Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.
Изгибающий момент: понятие и примеры
Когда на твёрдое тело действует изгибающий момент, противоположные стороны тела подвергаются различным силовым действиям: с одной стороны возникает сжатие, а с другой — растяжение. Именно эти силы стремятся вернуть тело в его исходное положение, что создает изгиб.
Примером изгибающего момента может служить мост. Когда на мост действуют нагрузки, например, транспортные средства, возникает изгибающий момент в конструкции моста. В это время деформация происходит в конкретных участках моста, где возникают сжатие и растяжение материала. Прочность и стабильность моста определяются величиной изгибающего момента.
Еще одним примером может служить балка. Приложение изгибающего момента к балке приводит к появлению сжатия и растяжения в разных частях балки, изгибая ее. Изгибающий момент влияет на прочность и деформацию балки.
| Примеры изгибающего момента |
|---|
| Мосты |
| Балки |
| Строительные конструкции |
| Архитектурные элементы |
| Производственное оборудование |
Изгибающий момент в физике и инженерии
Изгибающий момент широко применяется в физике и инженерии, особенно при рассмотрении законов деформации твердых тел. Он играет важную роль в механике материалов и конструкций, а также при проектировании различных механизмов и оборудования.
Пример изгибающего момента можно наблюдать в случае изгибания балки. Когда на балку действует вертикальная сила, возникает изгибающий момент, который вызывает искривление балки. Изгибающий момент зависит от величины силы, расстояния от оси изгиба до точки приложения силы и геометрических параметров балки.
Другим примером изгибающего момента является механизм действия рулем автомобиля. Когда водитель поворачивает руль, он прикладывает силу, вызывая изгибающий момент на валу рулевого механизма. Это позволяет автомобилю изменять направление движения.
Изгибающий момент является важным аспектом при анализе и расчете различных конструкций и деталей. Понимание его принципов позволяет инженерам и физикам разрабатывать более эффективные и безопасные конструкции.
Эпюры при поперечном изгибе
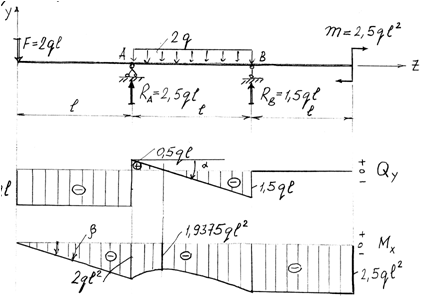
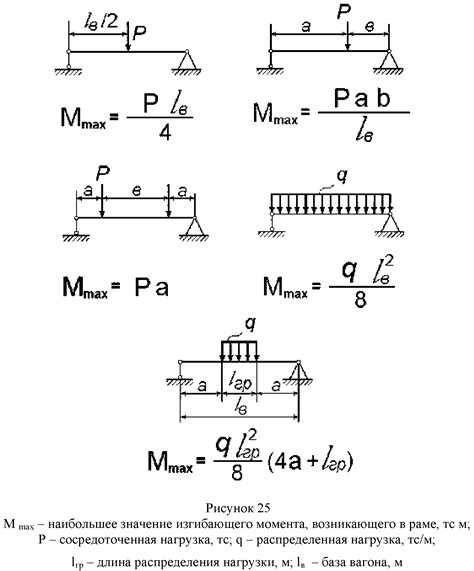
Построение эпюр Q и M для балки, изображенной на рис. 3
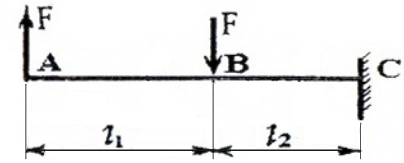
проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.
I силовой участок (AB): 0 ≥ z1 ≥ l1 (рис. 4, а, г) Q(z1)= F=const, на всем участке постоянная величина, M(z1)=F×z1, уравнение прямой, график строим по двум граничным точкам: M(z1=0)=F×0=0 – в сечении A; M(z1=l1)=F× l1 — в сечении B.
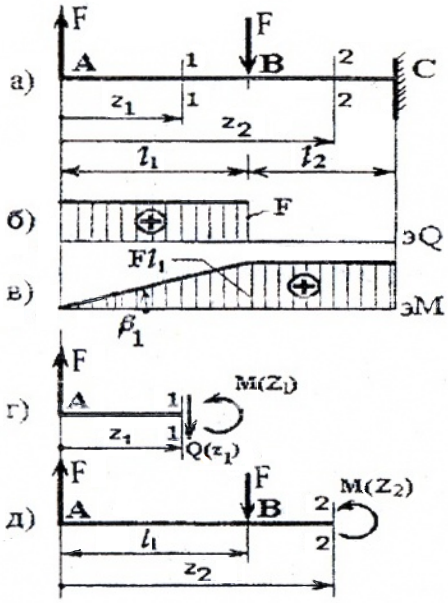
Опасным является сечение B, в котором действуют Qmax=F, Mmax=Fl1.
Геометрическая проверка эпюр
Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем: Для всех силовых участков находим:
11
На участке “BC”:
Изгиб как фактор прочности
Изгиб — это одно из основных механических воздействий на прочность конструкции. Возникает изгиб, когда на элемент действуют силы, приводящие к его изгибанию.
Важное понятие, связанное с изгибом, — это момент изгиба. Момент изгиба — это сила, приложенная к элементу в поперечном направлении, создающая изгибающий момент
Момент изгиба приводит к появлению напряжений в материале элемента конструкции.
Прочность изгибающегося элемента зависит от его геометрии, свойств материала и приложенных нагрузок. Для анализа прочности изгибающегося элемента используется так называемая формула изгиба:
σ = M / S
где:
- σ — напряжение в материале элемента;
- M — момент изгиба;
- S — момент сопротивления элемента (свойственная для него характеристика).
Момент сопротивления элемента зависит от его геометрии, в частности, от площади поперечного сечения. Чем больше момент сопротивления, тем выше прочность элемента при изгибе.
Примером элемента, находящегося под воздействием изгиба, может служить балка. Если на балку действуют силы, создающие изгибающий момент, то в материале балки возникают напряжения. Для обеспечения достаточной прочности балки при изгибе необходимо подобрать ее геометрию и материал.
Таким образом, изгиб играет важную роль в определении прочности конструкций и требует учета в проектировании и расчетах.
Правила знаков для поперечных сил
Внешняя сила, действующая на отбрасываемую часть балки и стремящаяся повернуть ее относительно сечения по ходу часовой стрелки, входит в алгебраическую сумму для определения поперечной силы () со знаком плюс (рис. 7.5, а). Заметим, что положительная поперечная сила () «стремится вращать» любую из частей балки также по ходу часовой стрелки.
Говоря простым языком: в сечении балки возникает поперечная сила, которую нужно определить и изобразить на эпюре поперечных сил. Чтобы правило знаков для поперечных сил выполнялось, нужно запомнить:
Если поперечная сила возникает справа от сечения, она направлена вниз, а если поперечная сила возникает слева от сечения – вверх (рис. 7.5, а).
Поперечная сила является внутренней силой, поэтому поперечная сила противоположна равнодействующей внешних сил, действующих на рассматриваемую часть балки. Поэтому если внешняя сила P (рис. 7.5, а) направлена вниз, то интересующая поперечная сила, возникающая от действия силы P, направлена вверх (и наоборот). Значит, внутренняя сила положительна, если внешняя сила, породившая ее, направлена противоположно направлению поперечной силы по правилу знаков.
Допустим, рассматривается правая часть балки (рис.7.5, а). Действует сила P, направленная вверх. По правилу, поперечная сила положительна, если направлена вниз (или внешняя сила P, породившая ее, направлена вверх).
Как измерить изгиб?
Изгиб – это деформация конструкции или материала, которая происходит под воздействием внешних сил, приводящая к изгибанию или изгибным напряжениям в объекте. Для измерения изгиба необходимо провести специальные измерения и расчеты.
Основным способом измерения изгиба является использование приборов и методов, таких как:
- Прогибометр: это прибор, который позволяет измерять величину прогиба объекта под воздействием внешних сил. Прогибометры могут быть аналоговыми или цифровыми и обычно имеют шкалу для чтения результатов.
- Метод штатива: этот метод используется для измерения изгиба путем фиксации объекта на специальном штативе и измерения прогиба с помощью рулетки или линейки.
- Метод опоры: в этом методе прогиб объекта измеряется путем определения прогиба относительно фиксированных опорных точек. Для измерения прогиба можно использовать специальные опорные конструкции или опорные плоскости.
После проведения измерений используются математические формулы и модели для расчета величины изгиба и определения изгибных напряжений. Для точных и надежных результатов измерений и расчетов рекомендуется обращаться к специалистам в области технической механики и использовать профессиональное оборудование.
Типы изгиба
В технической механике выделяются различные типы изгиба, которые влияют на поведение и прочность конструкций. Ниже рассмотрены основные типы изгиба:
-
Прогиб: Прогиб — это деформация конструкции, при которой она смещается в направлении, перпендикулярном к ее плоскости. Возникает в результате приложения внешних сил, приводящих к изгибающему моменту.
-
Растяжение сверху: Растяжение сверху — это ситуация, когда верхняя часть конструкции подвергается растяжению, а нижняя часть сжатию. Такой тип изгиба возникает, например, при нагружении балки в середине.
-
Сжатие сверху: Сжатие сверху — это ситуация, когда верхняя часть конструкции подвергается сжатию, а нижняя часть растяжению. Такой тип изгиба возникает, например, при нагружении балки на опоре.
-
Двойное изгибание: Двойное изгибание — это комбинация растяжения сверху и сжатия сверху, при которой и верхняя, и нижняя части конструкции подвергаются соответствующим напряжениям. Такой тип изгиба возникает, например, при нагружении балки с двух сторон.
Тип изгиба определяет характерные напряжения в материале конструкции и может быть учтен при расчете прочности и деформаций.
Сравнение типов изгиба
Тип изгиба
Растяжение сверху
Сжатие сверху
Прогиб
+
+
Растяжение сверху
+
—
Сжатие сверху
—
+
Двойное изгибание
+
+
В таблице приведено сравнение типов изгиба по наличию растяжения (+) или сжатия (-) в соответствующих частях конструкции.
Что такое изгибающий момент
В первой части цикла мы уже выяснили, что любые воздействия на материал и все виды сопротивления можно разложить по осям x, y, z на силы и моменты и получить шесть уравнений равновесия.
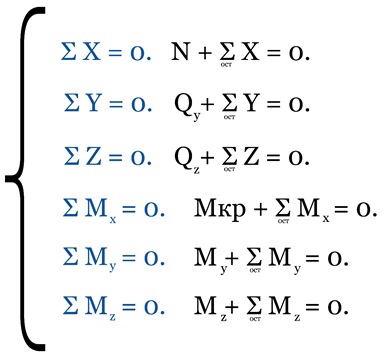
Тем не менее, если про силы мы уже поговорили достаточно подробно, то про моменты пока умолчали.
Момент – это количество «кручения». Для материальной точки он вычисляется произведением силы на плечо:
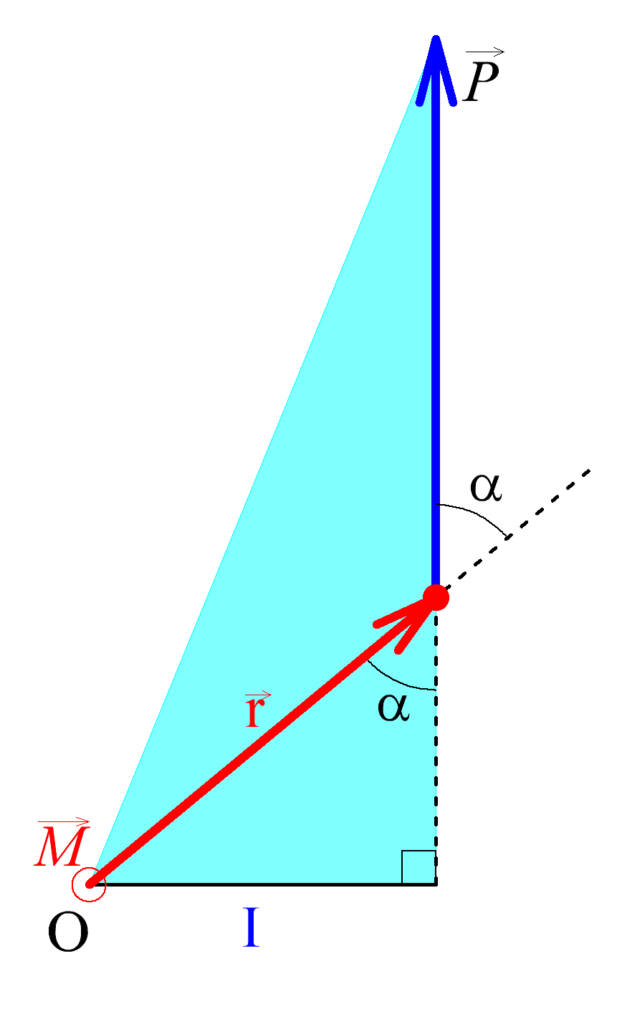 Момент — это произведение силы на плечо.
Момент — это произведение силы на плечо.
Проводим из точки перпендикулярно силе линию, её длину умножаем на силу. Это и будет момент кручения данной точки.
Помимо прочего, момент может задаваться парой параллельных, но противоположных по направлению сил. Тогда равнодействующая сил не изменится, а тело будет стремиться к изгибу.
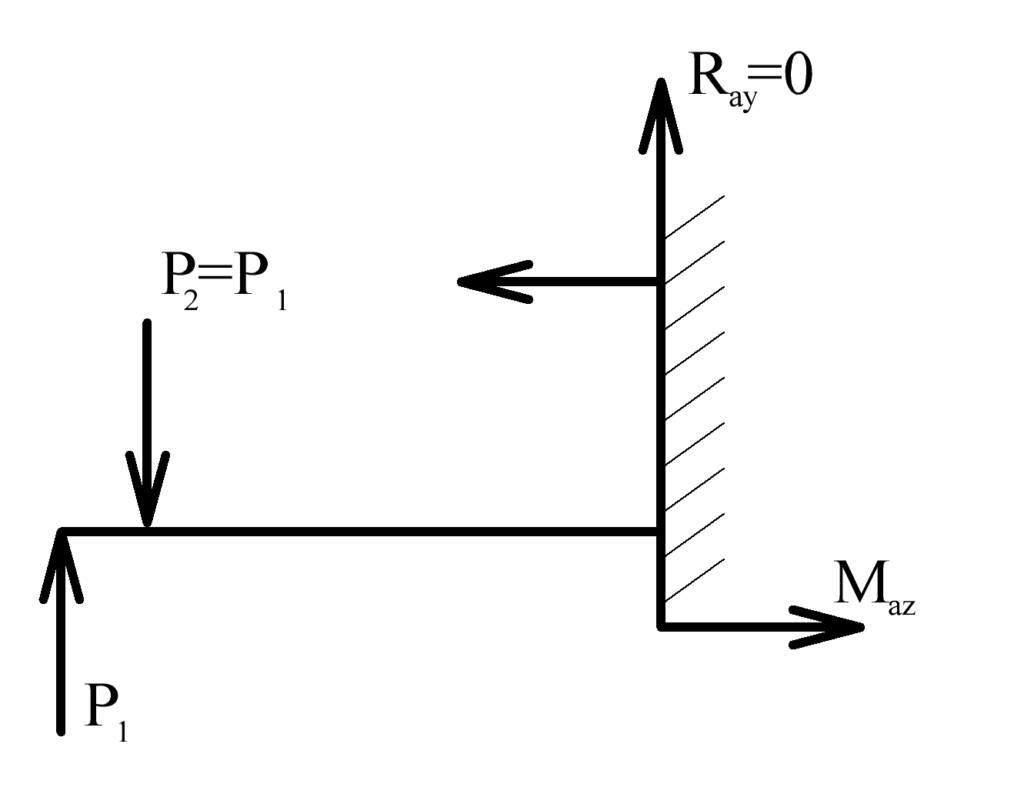 Момент Maz кручения задан парой сил.
Момент Maz кручения задан парой сил.
Изгибающий момент и поперечная сила
Для оценки параметров деформационных процессов, протекающих в различных конструкциях, применяют изгибающий момент и воздействующую поперечную силу. Их рассчитывают на основании уравнений равновесия. Каждое позволяет найти параметры каждого слоя балки при изгибе.
При проектировании конструкции для расчёта этих параметров учитывают следующие правилами:
- воздействие внешнего фактора, способного повернуть балку по часовой стрелке относительно проведенного сечения;
- создаётся изгибающий момент, способный привести к сжатию каждого из волокон балки (в уравнении его учитывают со знаком плюс);

Полученные результаты позволяют построить графическое изображение распределения сил и моментов на различных уровнях. Такие изображения называют эпюрами. С их помощью определяют прочность создаваемой конструкции.
Реакции опор.
Мы выяснили, впрочем, это и без нас было известно, что у всего есть предел. За пределом у человека — смерть, у строительной конструкции — разрушение, но за жизнь сражаются все. Когда мы давили на линейку пальцем в одном из мест, где линейка опиралась на книги, победить линейку нам не удалось и мы своим пальцем чувствовали, как линейка упиралась, но не прогнулась ни на миллиметр. Причем, чем сильнее мы давили на линейку, тем сильнее она упиралась, при этом сила, с которой мы давили на линейку была сравнима с силой отпора.
В реальном мире все очень сложно — любое вещество, даже очень простое, устроено очень непонятно. Одни вещества состоят из атомов, соединенных в кристаллическую решетку, при этом материал может быть монокристаллическим или поликристаллическим. В других веществах атомы входят в состав молекул, которые могут быть и простыми и очень сложными. Но между всеми этими атомами или молекулами существует строгая связь. Все эти атомы и молекулы держатся на определенном природой расстоянии и когда мы давим пальцем на линейку, то мы пытаемся уменьшить расстояние между атомами или молекулами, а молекулы да атомы этого не хотят и сопротивляются, говоря научным языком возникает напряжение, т.е. расстояние между атомами или молекулами уменьшается, но если палец убрать, то атомы и молекулы вернутся на свои места.
Мало того, когда мы давим на линейку, деформации возникают не только в веществе линейки, но и книги, в том месте где на книгу опирается линейка , в веществе стола, на котором лежат книги и так далее, до самого земного ядра. Кстати говоря, для некоторых веществ термин напряжение можно понимать буквально — этот эффект положен в основу работы пьезоэлементов, но не будем отвлекаться. Так вот когда мы давим пальцем на линейку в точке опоры, то часть энергии переходит в упругие деформации, часть в неупругие деформации, часть в нагрев вещества, еще какая-то часть в звуковые колебания и так далее, одним словом процесс сложный, но вот за что я люблю строительную механику, так это за то, что в строймехе все просто, потому как строительная механика придумана не для того, чтобы усложнять нам жизнь, а чтобы жизнь и, в частности, расчет строительных конструкций, упрощать.
В строительной механике этот сложный комплекс событий называется реакцией опоры. Считается, что когда мы прикладываем силу (сосредоточенную нагрузку) на опоре (см. рис.4.1), то возникает реакция опоры, численно равная приложенной нагрузке и направленная противоположно — красота! Таким образом, если мы приложили на опоре нагрузку 1 Ньютон, то на опоре возникает реакция тоже 1 Ньютон, при этом на второй опоре никакой нагрузки нет, поэтому и реакция опоры равна 0. Такое допущение позволяет заменить опоры, точнее опорные связи, реактивными силами — реакциями опор. Для простоты восприятия можно измерять силы в килограмм-силах, 1 кгс ≈ 10 Н (если быть более точным, то 1 кгс = 9.81 Н). И теперь, если рассматривать балку висящей в воздухе, то для того, чтобы балка не падала, другими словами находилась в состоянии статического равновесия, достаточно в одной точке приложить к балке две равные по значению, но противоположно направленные силы.
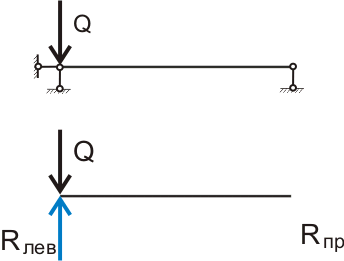
Рисунок 4.1. Замена опорных связей реактивными силами — опорными реакциями.





























