Что такое знаковое событие?

сложное событие и простое событие

Далее мы объясним разницу между сложным событием и простым событием, поскольку это два разных понятия, которые часто путают, хотя они и являются базовыми.

Простое событие (или простое событие) — это одиночный результат случайного эксперимента, тогда как сложное событие (или сложное событие) — это набор из двух или более возможных результатов. Другими словами, сложное событие представляет собой комбинацию простых событий.

Например, в эксперименте с броском кубика получение лица с номером 1 — это простое событие. С другой стороны, выпадение числа меньше 6 — это событие, состоящее из пяти простых событий (1, 2, 3, 4 и 5).

В этом случае, поскольку события равновероятны, вероятность одного события можно легко определить, разделив его на общее количество возможных исходов:

Вероятность составного события рассчитывается путем деления общего количества благоприятных случаев на общее количество возможных исходов. Например, в сложном случае выпадения числа меньше 6 при броске игральной кости имеется пять благоприятных случаев, поэтому вероятность выпадения равна 5/6.

В теории вероятностей эта формула называется правилом Лапласа.

➤ См.: примеры простых событий

Понятие вероятности события

Определение 2

Вероятностью события будем называть число, которое обозначает степень возможности, что такое событие произойдет.

Вероятность события обозначается как $P(A)$

Чтобы определить границы значения этого числа введем понятие достоверного и невозможного событий.

Определение 3

Достоверным событием будем называть такое, которое произойдет при любых обстоятельствах.

Примером такого события может быть следующее: Сумма «точек» на классической кости всегда равняется $21$.

Вероятность такого события мы будем принимать за единицу.

Определение 4

Невозможным событием будем называть такое, которое не может произойти ни при каком обстоятельстве.

Примером такого события может быть следующее: При игре в «очко» игрок набрал $1$ очко.

Вероятность такого события мы будем принимать за $0$.

То есть значение вероятности любого события содержится в отрезке $$.

В современной теории вероятности принято выделять четыре определения для вероятности: классической, геометрическое, статистическое и аксиоматическое определения. Рассмотрим их отдельно.

Виды событий

В теории вероятностей события бывают невозможными, случайными и достоверными.

Невозможное событие

Это то, которое уже известно, что в ходе испытания НЕ произойдёт, т. е. вероятность данного события равна нулю. Например: при бросании одной игральной кости (один раз), какова вероятность того, что выпадет 7 очков?

Случайное событие

Это событие может произойти или нет, обычно оно именно случайное. Например: при бросании игральной кости, какова вероятность того, что выпадет чётное число очков?

Достоверное событие

Это то, которое в ходе испытания обязательно произойдёт, т. е. вероятность данного события равна 1. Например: при бросании игральной кости, какова вероятность того, что она не останется в воздухе, а упадёт?

1.2. Краткая историческая справка

Первые работы, в которых зарождались основные понятия
теории вероятностей, представляли собой попытки создания теории азартных игр
(Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI—XVII
вв.).

Следующий этап развития теории вероятностей связан с именем
Якоба Бернулли A654—1705). Доказанная им теорема,
получившая впоследствии название «Закона больших чисел», была первым
теоретическим обоснованием накопленных ранее фактов.

Дальнейшими успехами теория вероятностей обязана Муавру,
Лапласу, Гауссу, Пуассону и др.

Новый, наиболее плодотворный период связан с именами
П.Л. Чебышева 1821—1894) и его учеников А.А. Маркова 1856—1922) и А.М. Ляпунова
1857—1918).

В этот период теория вероятностей становится стройной
математической наукой. Ее последующее развитие в нашей стране обязано в первую
очередь таким математикам, как С.Н. Бернштейн, В.И. Романовский,
А.Н. Колмогоров, А.Я. Хинчин, Б. В. Гнеденко, Н. В. Смирнов и др.

Основные понятия

Мы упомянули слова «событие» и «вероятность», но не рассказали, что они вообще значат в контексте теории вероятностей. Давайте разбираться.

События

Событие — это всё, что может произойти, когда мы совершаем какое-то действие. Например, если мы бросаем монетку, то событие — это выпадение орла или решки. Чтобы обозначать события, используют заглавные буквы латинского алфавита. Например, для орла можем выбрать букву A, а для решки — B.

Существует много разных видов и классификаций событий, но в этой статье мы остановимся на основных четырёх:

• Достоверные — те, которые точно произойдут. Если бросить стакан на пол, то с вероятностью 100% он полетит вниз.
• Невозможные — те, которые никогда не произойдут. Если бросить тот же стакан на пол, то он никогда не полетит вверх (мораль: не стоит бросать стаканы на пол, если, конечно, вы не на МКС).
• Случайные — те, которые могут произойти, а могут и не произойти. Например, если мы бросаем игральный кубик, то не можем с уверенностью сказать, что выпадет число 2.
• Несовместимые — те, которые исключают друг-друга. Например, при подбрасывании монетки может выпасть либо орёл, либо решка — оба одновременно они выпасть не могут.

Стать экспертом по теории вероятностей очень просто — нужно всего лишь завести кошку и наблюдать за нейИнфографика: Оля Ежак для Skillbox Media

Если собрать все несовместимые события вместе, они будут называться полной группой событий. Это множество событий, одно из которых обязательно случится, если мы совершаем действие, а другие — не произойдут никогда. Например, когда мы бросаем игральный кубик, может выпасть только одна из сторон.

Вероятности

Вероятность — это число, которое обозначает шанс возникновения события. Например, вероятность выигрыша в лотерею может составлять 1 к 1 000 000.

Мы записывали значения вероятностей в процентах и отношениях, но математикам удобнее располагать их в диапазоне от 0 до 1. Если вероятность равна 0, то событие никогда не произойдёт, а если 1 — точно произойдёт. Всё, что посередине, — это случайные события.

Самый простой способ вычислить вероятность — поделить число благоприятных событий на общее число возможных событий. Например, если всего в колоде 36 карт, а мы хотим достать короля пик, то вероятность этого события равна 1/36, или 0,03. Если бы нас устроил любой из королей, то вероятность была бы равна 4/36 — то есть 0,1.

Начальная вероятность того, что вы наткнётесь на мину в самом начале игры в «Сапёра», — около 20%. С каждой открытой клеткой этот шанс увеличивается. Но это если полагаться только на удачу.

К формулам мы ещё вернёмся, а пока отметим, что вероятность — это не всегда точное предсказание, а лишь оценка шанса возникновения события. Как следует из закона больших чисел, если шанс выпадения орла и решки равен 50%, это не означает, что они будут выпадать по очереди.

Ещё вероятность может быть условной — или зависеть от другого события. Например, если мы хотим вытащить любой туз из колоды карт, шанс равен 4/36. Но если до этого кто-то уже вытащил одного туза, то вероятность будет равна 3/35. Это потому, что в колоде стало на одну карту меньше и количество благоприятных событий тоже уменьшилось.

1.1. Предмет теории вероятностей

Наблюдаемые нами события (явления) можно подразделить на
следующие три вида: достоверные, невозможные и случайные.

Достоверным называют событие, которое обязательно
произойдет, если будет осуществлена определенная совокупность условий .
Например, если в сосуде содержится вода при нормальном атмосферном давлении и
температуре 20°, то событие «вода в сосуде находится в жидком состоянии» есть
достоверное. В этом примере заданные атмосферное давление и температура воды
составляют совокупность условий .

Невозможным называют событие, которое заведомо не
произойдет, если будет осуществлена совокупность условий S.
Например, событие «вода в сосуде находится в твердом состоянии» заведомо не
произойдет, если будет осуществлена совокупность условий предыдущего примера.

Случайным называют событие, которое при
осуществлении совокупности условий S может либо
произойти, либо не произойти. Например, если брошена монета, то она может упасть
так, что сверху будет либо герб, либо надпись. Поэтому событие «при бросании
монеты выпал «герб» — случайное. Каждое случайное событие, в частности выпадение
«герба», есть следствие действия очень многих случайных причин (в нашем примере:
сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть
влияние на результат всех этих причин, поскольку число их очень велико и законы
их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу
предсказать, произойдет единичное событие или нет, — она просто не в силах это
сделать.

По-иному обстоит дело, если рассматриваются случайные
события, которые могут многократно наблюдаться при осуществлении одних и тех же
условий ,
т. е. если речь идет о массовых однородных случайных событиях. Оказывается, что
достаточно большое число однородных случайных событий независимо от их
конкретной природы подчиняется определенным закономерностям, а именно
вероятностным закономерностям. Установлением этих закономерностей и занимается
теория вероятностей.

Итак, предметом теории вероятностей является изучение
вероятностных закономерностей массовых однородных случайных событий.

Знание закономерностей, которым подчиняются массовые
случайные события, позволяет предвидеть, как эти события будут протекать.
Например, хотя, как было уже сказано, нельзя наперед определить результат одного
бросания монеты, но можно предсказать, причем с небольшой погрешностью, число
появлений «герба», если монета будет брошена достаточно большое число раз. При
этом предполагается, конечно, что монету бросают в одних и тех же условиях.

Методы теории вероятностей широко применяются в различных
отраслях естествознания и техники: в теории надежности, теории массового
обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы,
теории ошибок наблюдений, теории автоматического управления, общей теории связи
и во многих других теоретических и прикладных науках. Теория вероятностей служит
также для обоснования математической и прикладной статистики, которая в свою
очередь используется при планировании и организации производства, при анализе
технологических процессов, предупредительном и приемочном контроле качества
продукции и для многих других целей.

В последние годы методы теории вероятностей все шире и шире
проникают в различные области науки и техники, способствуя их прогрессу.

Операции с составными событиями

С составными событиями можно выполнять следующие операции:

Объединение составных событий : объединение двух разных событий (или событий) A и B равно множеству событий A плюс множеству событий B.

Например, если составное событие A соответствует числам {1,3,4}, а составное событие B соответствует числам {2, 4}, объединение двух событий будет набором {1, 2, 3, 4). }.

Пересечение составных событий . Пересечение двух составных событий касается только событий, принадлежащих обоим наборам.

Если составное событие A состоит из чисел {1,3,4}, а составное событие B состоит из чисел {2, 4}, то пересечением двух событий будет только число 4.

Разница составных событий : разница двух событий A минус B равна событиям, которые подтверждают A, а не B.

Например, если составное событие A соответствует числам {1,3,4}, а составное событие B соответствует числам {2, 4}, разница между событием A минус событием B равна {1,3}.

Что такое алгебра событий

Когда мы считаем вероятности, нас может устраивать более чем один результат событий

Или другая ситуация — нам может быть важно, чтобы два события выполнялись вместе. В таких случаях на помощь приходит алгебра событий. Разбираемся, какие действия она позволяет совершать

Разбираемся, какие действия она позволяет совершать.

Дисклеймер: в этом разделе мы не рассматриваем вычитание и дополнение событий, потому что они довольно сложны для первого знакомства с теорией вероятностей. Возможно, скоро мы выпустим о них отдельную статью.

Сложение (объединение) событий

Сумма двух событий A + B — это сложное событие, которое произойдёт, если случится или событие A, или событие B, или оба одновременно.

Допустим, мы хотим вычислить вероятность выпадения на кубике стороны с числами 2 или 4. Обозначим событие «выпадение стороны 2» как A, а событие «выпадение стороны 4» как B. Так как у кубика всего шесть граней, вероятность выпадения каждой из этих сторон равна 1/6.

А так как нас интересует либо событие A, либо событие B, мы ищем сумму этих событий — A + B. Вычисляем соответствующие вероятности:

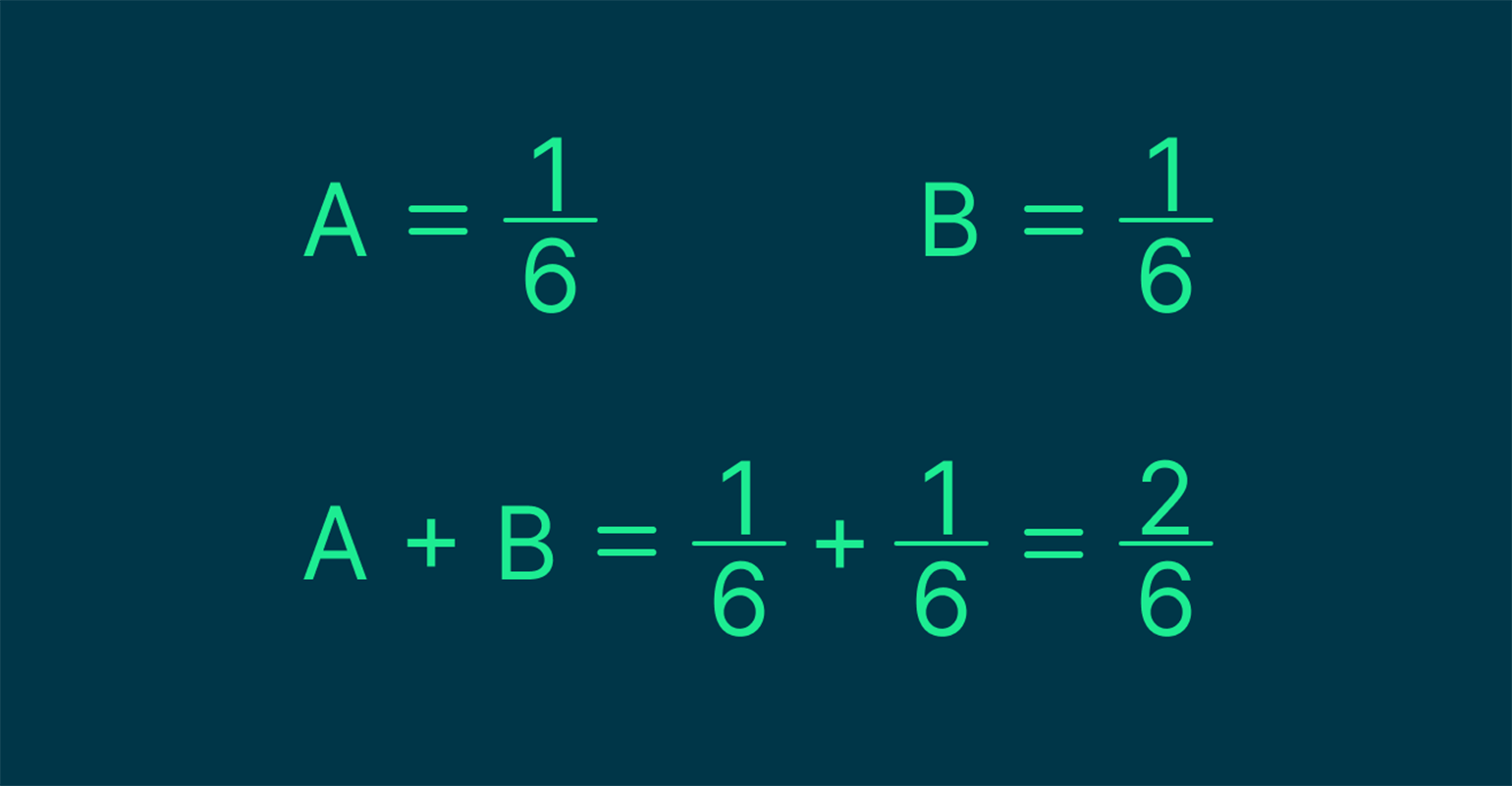
Изображение: Skillbox Media

Получается, что шанс выпадения стороны 2 или 4 при броске кубика равен 2 к 6, или 1 к 3, или 33%.

Правило сложения можно применять не только к двум событиям, но и к любому их количеству. Например, событие A + B + C + D произойдёт, если случится хотя бы одно из событий A, B, C, D или одна из их комбинаций, такая как A и C или A, C и D.

Умножение (пересечение) событий

Произведение событий A и B — это событие A × B, которое произойдёт, если случится и событие A, и событие B.

Допустим, мы бросаем монетку два раза и хотим понять, каков шанс, что оба раза выпадет решка. Напомним, что вероятность выпадения решки — 1/2.

Обозначаем события: A — решка выпадает первый раз, B — решка выпадает второй раз. Считаем вероятности:

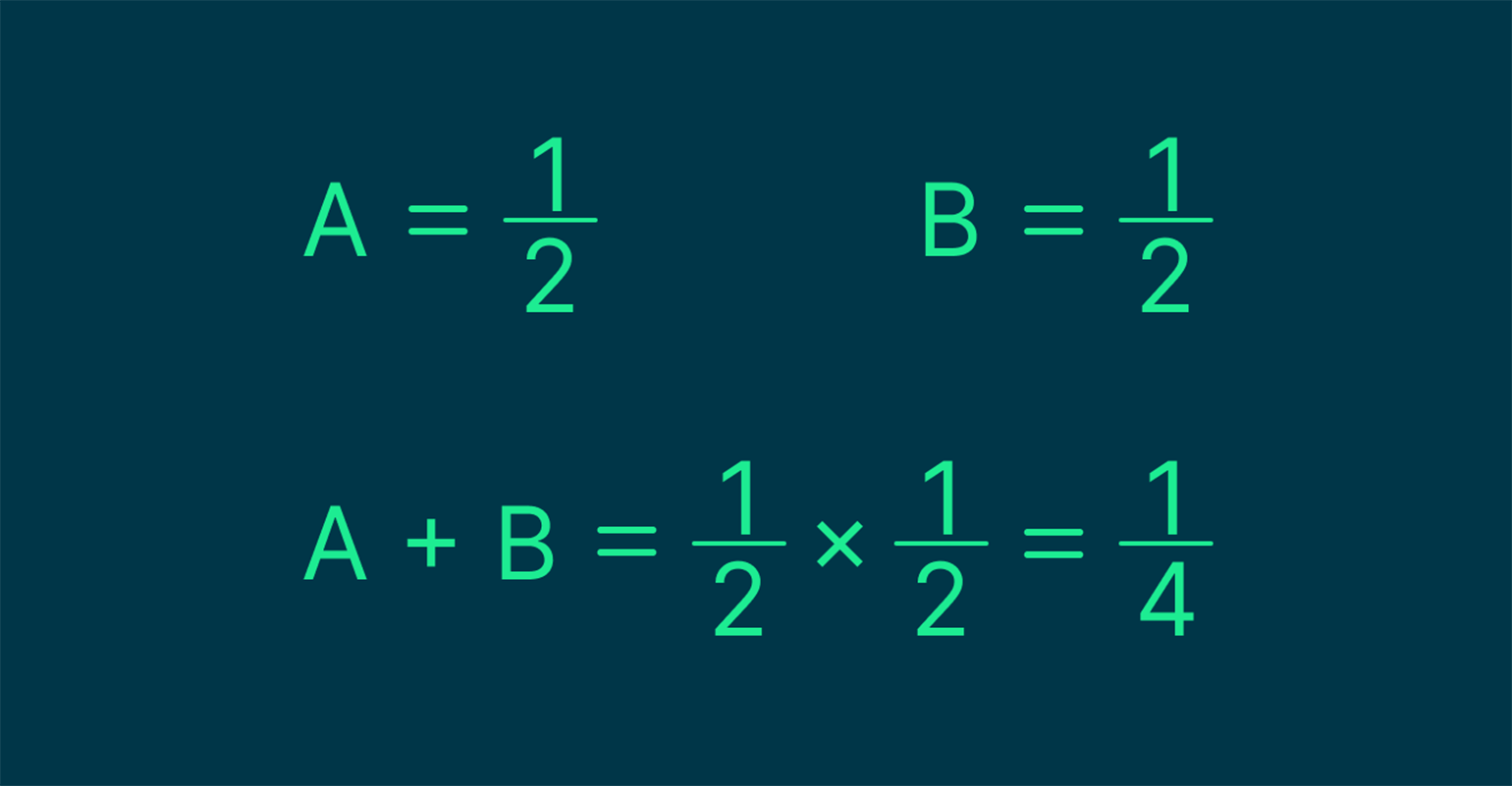
Изображение: Skillbox Media

Получаем, что шанс выпадения решки два раза подряд — 25%.

Как в случае с суммой, произведение событий можно считать для любого количества разных событий. Давайте продолжим пример с монеткой — теперь мы хотим, чтобы она выпала четыре раза подряд.

Добавляем два новых обозначения: C — решка выпадает третий раз, D — решка выпадает четвёртый раз. Вероятности всё те же, считаем их произведение:

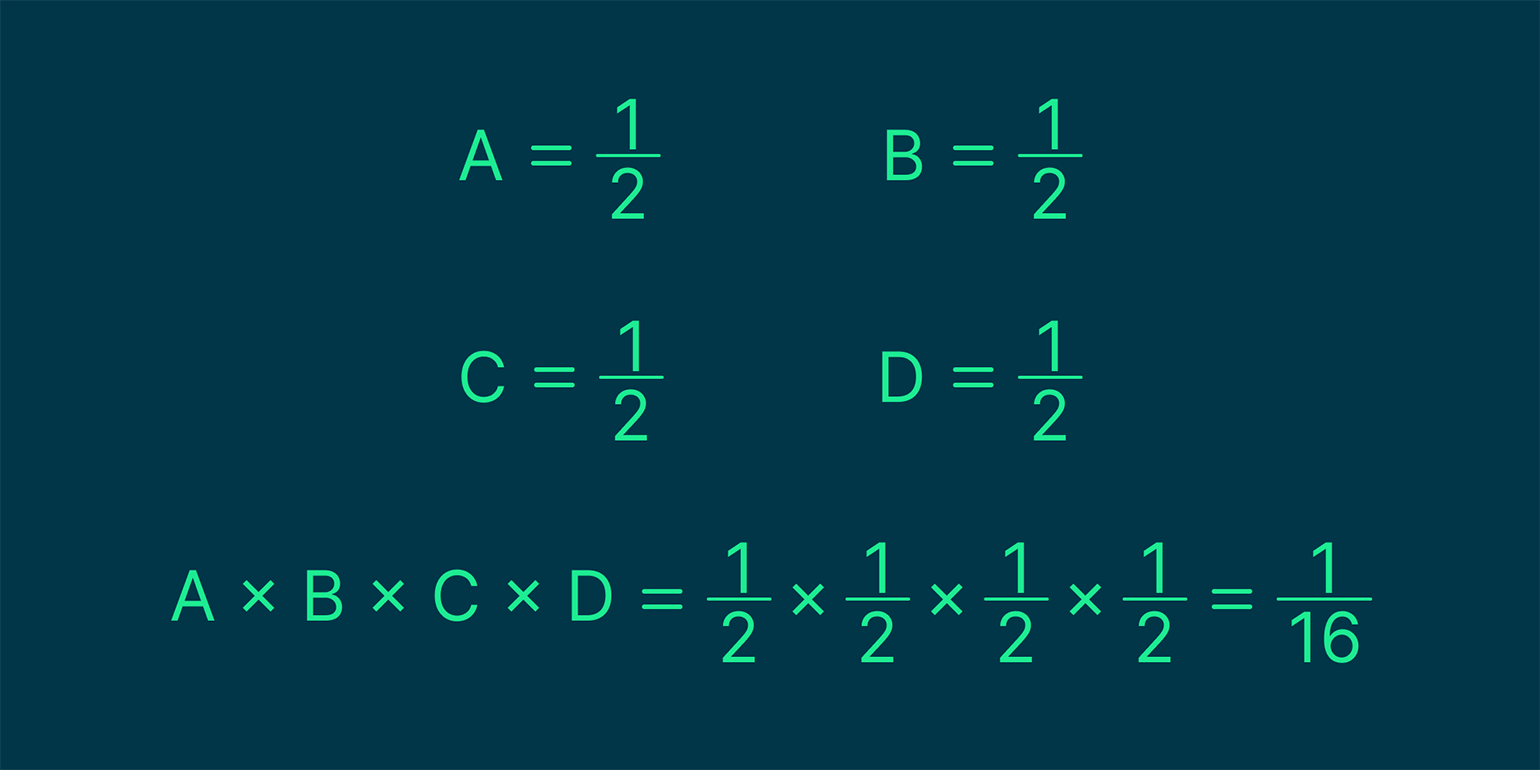
Изображение: Skillbox Media

Ответ — шанс выпадения решки четыре раза подряд равен 1 к 16, или 6,25%.

Сложение совместимых событий

Когда мы говорили о сложении вероятностей, мы использовали несовместимые события, поскольку при броске кубика может выпасть только одна сторона (или ребро, если вам сильно повезёт).

Теперь, когда мы познали тонкости вероятностного умножения, можно разобраться с тем, как складывать совместимые события. В этом случае из суммы двух событий нужно просто вычесть их произведение. Формула выглядит так:

P (A + B) = P (A) + P (B) — P (A ⋅ B)

Примером такого сложения может быть выбор случайных чисел. Допустим, у нас есть набор чисел от 1 до 10 и мы хотим найти вероятность того, что выбранное число будет или нечётным, или делиться на 7 без остатка.

Считаем вероятности:

• Событие A — число нечётное. Вероятность выбрать именно его — 5/10.
• Событие B — число делится на 7 без остатка. Вероятность — 1/10.

Так как число 7 удовлетворяет обоим условиям, мы имеем дело с совместимыми событиями — то есть они могут происходить одновременно. Подключаем формулу: сначала находим сумму вероятностей, а потом вычитаем из неё вероятность пересечения

Внимание на экран:

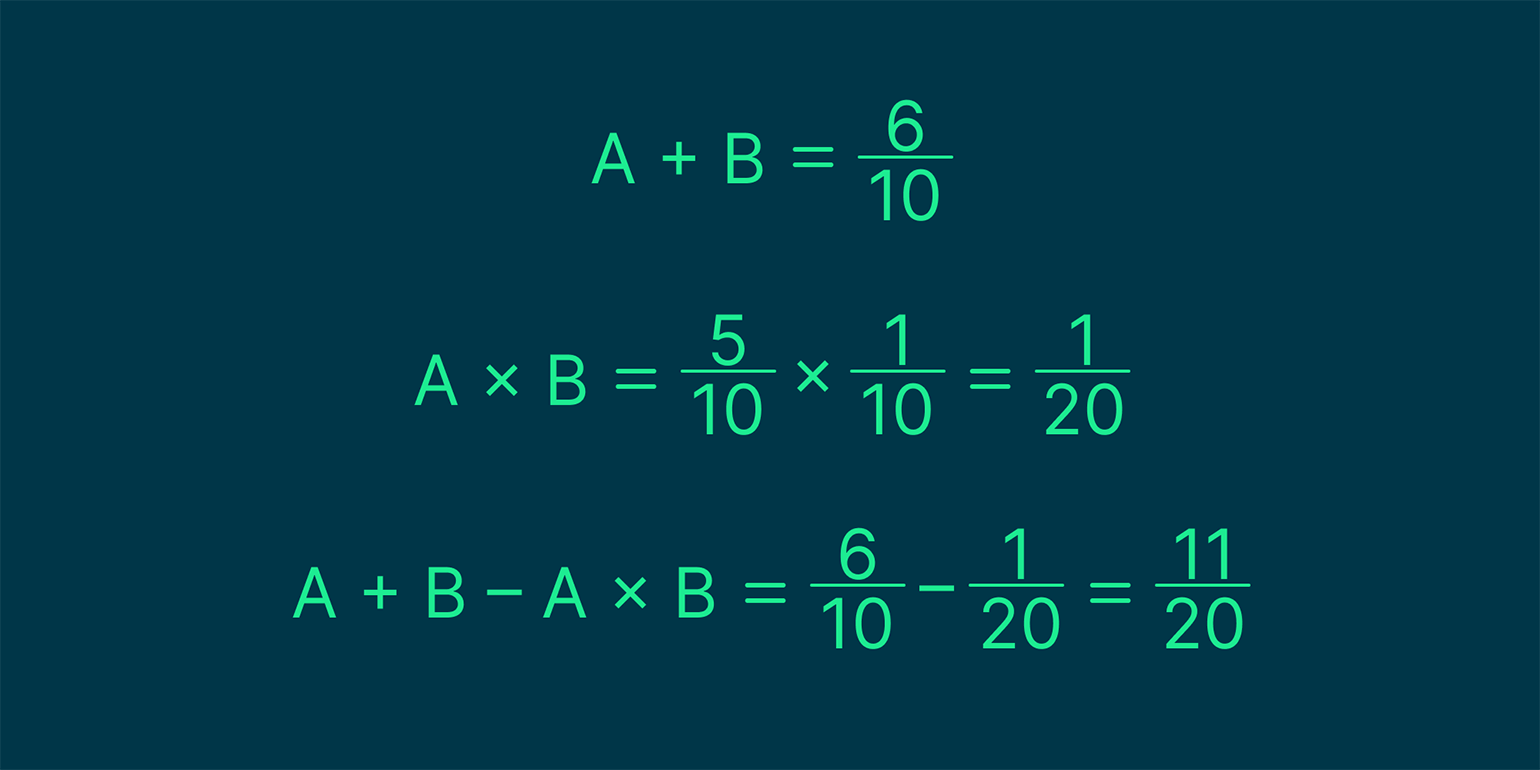
Изображение: Skillbox Media

Вуаля! Получается, что шанс выполнения одного из двух событий равен 11/20, или 55%.

Задачи

Пример 1

В классе 27 учеников. Из них:

17 изучали немецкий язык,

6 — английский,

2 — оба языка.

Найти вероятность того, что случайно выбранный ученик изучал хотя бы один язык.

Что мы знаем:

𝑃(N) = 17/27,

𝑃(A) = 6/27,

𝑃(N ∙ A) = 2/27.

Значит вместе это будет:

𝑃(N + A) = 𝑃(N) + 𝑃(A) − 𝑃(N ∙ A) = 17/27 + 6/27 − 2/27 = 21/27 = 7/9.

Пример 2

Лотерейные билеты пронумерованы от 1 до 100. Какова вероятность того, что в выбранном билете будет стоять число больше 40 или чётное число?

Что мы знаем:

P(>40) = 60/100 = 6/10 = 3/5

P(Ch) = ½ = 5/10

Логическое ИЛИ означает, что нам нужно произвести операцию сложения (т. е. сумма событий).

Нам понадобится формула сложения совместных событий P(A + B) = P(A) + P(B) — P(AB).

Для этого нам нужно узнать сколько будет P(>40 . Ch), для этого используем формулу P(AB) = P(A) . P(B).

P(>40 . Ch) = P(>40) . P(Ch) = ⅗ . ½ = 3/10

Теперь можем подставить всё в формулу P(A + B) = P(A) + P(B) — P(AB):

P(>40 + Ch) = P(>40) + P(Ch) — P(>40.Ch) = 6/10 + 5/10 — 3/10 = 8/10 = ⅘.

Пример 3

В финале международного турнира по стрельбе из лука участвовали 8 спортсменов: 3 американца, 1 англичанин, 1 немец, 1 француз и 2 русских. Какова вероятность того, что хотя бы один русский попадёт в тройку лучших, учитывая, что все спортсмены имеют равные условия для получения медали (золотой, серебряной и бронзовой).

Что мы знаем:

Когда в вопросе появляется «хотя бы один», можно «пойти от противного» — мы должны найти вероятность того, что этого не произойдёт (на пьедестале русских не будет), а затем вычесть это из 1.

P (никакой русский не выиграет золото) = 6/8 = 3/4

P (никакой русский не выиграет серебро) = 5/7 (убираем золотую медаль)

P (никакой русский не выиграет бронзу) = 4/6 = 2/3 (убираем золотую и серебряную медали)

P (на пьедестале не будет русских) = 3/4 x 5/7 x 2/3 = 30/84 = 5/14

P (хотя бы один русский на пьедестале) = 1 – 5/14 = 14/14 – 5/14 = 9/14.

§ 2. Независимость

Определение 19.
События и называются независимыми, если
.

Пример 19.

1. Точка с координатами , бросается наудачу в единичный квадрат
со сторонами, параллельными осям координат. Доказать, что для любых события и независимы.

2. Точка с координатами , бросается наудачу в
треугольник с вершинами , и .
Доказать, что события и зависимы.

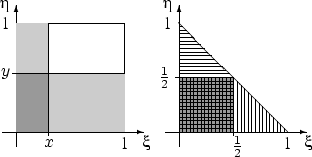
1. Решение. Рассмотрим (разобрать остальные случаи).
Тогда , , ,
т.е. события и независимы.

2. Решение. Вычислив соответствующие площади в треугольнике, получим:
, , ,
т.е. события и зависимы.

Естественно считать события и независимыми, когда
при условии, что произошло, остаётся такой же, как и безусловная.
Убедимся, что этим свойством обладают события, независимые согласно
.

Свойство 4.
Пусть . Тогда события и независимы тогда и только тогда, когда
.
Если , то события
и независимы тогда и только тогда, когда
.

Упражнение 23.
Доказать, пользуясь определением условной вероятности.

Свойство 5.
Пусть события и .
Тогда независимыми они будут только в том случае, если
или .

Это свойство (а вы его доказали?) означает, что в невырожденном случае (когда вероятности событий
положительны) несовместные события не могут
быть независимыми. Зависимость между ними  просто причинно-следственная:
если , то , т.е. при выполнении
событие не происходит. Это свойство можно сформулировать иначе:
в невырожденном случае независимые события просто обязаны пересекаться, т.е. быть
совместными.

Упражнение 24.
Доказать с помощью свойства , что событие , вероятность которого равна нулю или единице,
не зависит ни от какого события , в том числе и от самого себя.

Свойство 6.

Если события и независимы, то независимы
и события и ,
и , и .

Доказательство. Так как , и события
и несовместны,
то .
Поэтому

.

Вывести отсюда остальные утверждения.

QED

Если у нас не два, а большее число событий, выполнение только одного равенства

вовсе не означает независимости этих событий. Например, при таком равенстве
события и вполне могут оказаться зависимыми (привести
соответствующий пример).
Хотелось бы независимостью нескольких событий считать такое свойство, при котором
любые комбинации этих событий оказываются независимыми между собой, например
и независимы.

Определение 20.

События называютсянезависимыми в совокупности, если для любого и любого
набора различных меж собой индексов имеет место равенство:

(6)

Замечание 8.
Если события независимы в совокупности, то
они попарно независимы, т.е. любые два события
независимы. Достаточно в равенстве
взять . Обратное, как показывает следующий пример, неверно: из попарной независимости
не вытекает независимость в совокупности.

Пример 20.  (пример
Бернштейна).

Рассмотрим правильный тетраэдр, три грани которого окрашены соответственно
в красный, синий, зелёный цвета, а четвёртая грань содержит все три цвета.
Событие (соответственно, , ) означает, что выпала грань, содержащая
красный (соответственно, синий, зелёный) цвета.

Вероятность каждого из этих событий равна 1/2, так как каждый цвет
есть на двух гранях из четырёх. Вероятность пересечения
любых двух из них равна 1/4, так как только одна грань из четырёх содержит два цвета.
А так как 1/4 = 1/2 · 1/2, то все события попарно независимы.

Но вероятность пересечения всех трёх тоже равна 1/4, а не 1/8,
т.е. события не являются независимыми в совокупности.

Заметьте, что равенство выполнено при , но не при .

Next:  Формула полной вероятности
  Up:  Условная вероятность, независимость
  Previous:  Условная вероятность

Сергей Натанович Бернштейн (5.03.1880 26.10.1968)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Событие как элемент сюжета

Согласно У. Д. Чейфу, в процессе построения суждения из ситуации или события выделяются предметы, которым принадлежат роли в границах данного события. Согласно А. Ф. Папиной, событие выражает основное сообщение. В качестве видовых понятий категория событие включает в себя:

• событие,
• процесс,
• состояние,
• факт.

Событие выражается при помощи следующих средств: процессные, событийные предикаты, событийные существительные, предикаты со значением факта и т.д. Событие бывает вымышленным, реальным, художественным. К тому же, выделяется оппозиция реальное событие – виртуальное.

Определение 2

Художественное событие – это результат творчества автора, способ выражения фактов личной либо общественной жизни человека, фактов существования природы в поэтическом и прозаическом тексте.

Существует несколько видов художественных событий:

• Художественное событие – обобщение;
• Конкретное художественное событие;
• Поэтически трансформированное художественное событие;
• Художественное событие-абстракция.

Ю. М. Лотман в книге «Структура художественного текста» дает двоякое определение события. С одной стороны, событие по Лотману – это перемещение действующего лица через границу семантического поля. С другой стороны – это некое отклонение от существующих норм, то, что произошло, хоть и могла не произойти, включая и пересечение запрещающей границы, утвержденной бессюжетной структурой.

Событие «сюжетологии» целиком происходит в действительности, о которой ведется речь. Событие нарратологии относится к действительности рассказывания – миру читателя и автора. Тое есть, персонаж, как и семантика каких-либо выражений и слов, группируемая в семантические поля с точки зрения читателя, с внутренней точки зрении я- моменты и элементы изображенной в произведении действительности. Сам текст, напротив, является элементом действительности читателя, которой принадлежат границы выражений и слов, присутствующих в тексте. Однако пересекать их персонаж со своей точки зрения не способен. В мире персонажа для него существуют границы, которые разделяют моменты времени или части пространства, имеющие значение для его жизни. Перемещение персонажа через данные границы формирует сюжет.

Гегель противопоставляет происшествию событие, используя понятие цели. Он пишет, что в этом отношении сначала необходимо установить различие между происходящим и действием, принимающем в эпическом произведении форму события. Просто происходящее – это внешняя сторона и реальность любого человеческого действия, которое не требует осуществления какой-либо особенной цели, и любое внешнее изменение вообще в явлении и облике всего существующего.

Данное суждение принадлежит к теории сюжета – то есть, имеется в виду мир персонажа соотношение между обстоятельствами и его целью.

Замечание 1

Событие – это реализация намерения, то есть совпадение «внешнего» и «внутреннего». Событием можно считать и столкновение с препятствиям, отсрочивающими или исключающими исполнение поставленной цели.

Если соединить определения, данные Лотманом и Гегелем, можно сформулировать общее для этих трактовок содержание – «сюжетологическое» определение категории события. Таким образом, событие, как элемент сюжета – это переход действующего лица через границу, которая разделяет семантические поля в тексте (с точки зрения читателя и автора) или сферы времен и пространства в изображенном мире — с точки зрения персонажа, связанной с его представлением о намеченной цели и препятствиях к достижению этой цели.

Основные принципы знаковой ситуации в современном мире

Знаковая ситуация – это особое явление, которое возникает вследствие взаимодействия между субъектом и знаком. В современном мире знаковые ситуации играют важную роль в коммуникации, образе жизни и взаимодействии людей.

Взаимодействие субъекта и знака

Одним из основных принципов знаковой ситуации является взаимодействие субъекта и знака. Знак представляет собой некоторый символ, который несет определенную информацию или сообщение. Субъект воспринимает этот знак и декодирует его, понимая значение и смысл, который он несет. Таким образом, взаимодействие субъекта и знака позволяет передавать информацию и общаться на уровне символов и смыслов.

Культурная обусловленность знака

Каждый знак имеет свое значение и смысл, который культурно обусловлен. В разных культурах и языках одни и те же символы могут иметь разное значение. Например, цвета могут быть символами удачи, печали или смерти в разных культурах. Таким образом, культурная обусловленность знака является важным принципом знаковой ситуации, который необходимо учитывать при общении и взаимодействии с другими людьми.

Контекстуальность знака

Знак всегда существует в определенном контексте – ситуации или окружении, в котором он используется. Контекстуальность знака означает, что его значение зависит от ситуации и окружающих условий. Например, трафиковый знак «Стоп» имеет одно значение на дороге, а совершенно другое значение в ситуации игры в детском саду. Поэтому при взаимодействии с знаками необходимо учитывать контекст и ситуацию, в которой они используются.

Индивидуальная интерпретация знака

Каждый человек имеет свой уникальный опыт и представления о мире, поэтому индивидуальная интерпретация знака может отличаться у разных людей. Например, один человек может воспринимать знак «Улыбнитесь» как призыв к дружелюбию и радости, а другой человек может воспринимать его как насмешку или иронию. Поэтому взаимодействие с знаками также предполагает учет индивидуальных различий и особенностей каждого человека.

Примеры знаковых ситуаций в современном мире:

• Интернет и социальные сети, где знаки (эмодзи, хасhtags) используются для общения и передачи смысла
• Реклама и медиа, где знаки используются для привлечения внимания и передачи информации
• Дорожные знаки и сигналы, которые регулируют движение и обеспечивают безопасность на дорогах
• Пиктограммы и символы, используемые во всем мире для обозначения мест, услуг и объектов
• Язык жестов, который используется людьми с нарушениями слуха для коммуникации и передачи информации

Важные принципы знаковой ситуации:
Название
Описание

Взаимодействие субъекта и знака
Субъект воспринимает и декодирует знак, понимая его значение и смысл

Культурная обусловленность знака
Значение знака зависит от культурных и языковых особенностей

Контекстуальность знака
Значение знака зависит от ситуации и окружающих условий

Индивидуальная интерпретация знака
Каждый человек может индивидуально интерпретировать знак в соответствии со своим опытом и представлениями

Примеры задач

Пример 1

Найти вероятность того, что наугад вытащенная из колоды карт будет бубновой масти (сумма карт в колоде кратна $4$-м).

Решение.

Так как количество карт кратно четверке, то пусть всего карт будет $4k$. Тогда каждой масти карт будет $k$ штук (так как мастей $4$ и их количество одинаково).

При решении этой задачи будем использовать определение $5$. Во введенных нами обозначениях, получим что в определении $5$ мы будем иметь

$N=4k,n=k$

Следовательно

$P=\frac{k}{4k}=\frac{1}{4}$

Ответ: $\frac{1}{4}$.

Пример 2

Пусть нам дана точка $(a,b)$, где $-5

Решение.

Тут мы будем использовать геометрическое определение. Изобразим вначале область, в которую в принципе может попасть эта точка (рис. 1).

Из этого рисунка видим, что

$S=8\cdot 5=40,s=3\cdot 3=9$

Тогда из геометрического определения:

$P=\frac{9}{40}$
Ответ: $\frac{9}{40}$.

Значимый

Значимость события может быть связана с его воздействием на общество, на индивидуальный опыт и восприятие человека. Значимые моменты в жизни людей обычно связаны с сильными эмоциями, восторгом или горем.

В контексте знаковых событий, значимость может быть определена их способностью вызвать коллективную реакцию, стать символом или знаком определенных ценностей или идей

Значимые события часто имеют долгосрочное влияние на общественное или культурное развитие, их важность может быть оценена по их историческому, социальному или культурному значению

Оценка значимости событий субъективна и может зависеть от контекста и восприятия разных групп людей. Однако, существуют события, которые широко признаются как значимые и имеют значительный отпечаток на мировой истории и культуре.

Примеры значимых событий в истории: Великая Октябрьская социалистическая революция, Первая и Вторая мировые войны, Лунная экспедиция, Падение Берлинской стены. Эти события оказали огромное влияние на политическую, социальную и культурную ситуацию и хорошо известны всему миру.

Характеристики значимых событий:
Значение
Важность
Событие имеет важное значение и влияет на множество людей или общество в целом.
Символичность
Событие становится символом или знаком определенных ценностей, идей или изменений.
Долгосрочное влияние
Значимое событие имеет долговременные последствия и оказывает влияние на экономику, политику, культуру или общество в целом.
Массовая реакция
Событие вызывает широкую реакцию и обсуждение среди множества людей или сообщества.

Геометрическое определение

Геометрическое определение применяется для случая, когда количество равновозможных событий будет бесконечно. Здесь, для введения геометрического определения рассмотрим следующий пример. Для игры дартс берем круг площадью $S$ и разбиваем его на несколько кругов. Какова вероятность, что дротик попадет в центральный круг? (Исключим здесь случаи полного непопадания в поле). Очевидно что равновозможных событий здесь будет бесконечно (как и общих событий) так как круг содержит в себе бесконечное число точек. Пусть площадь центрального круга равняется $s$. Тогда мы сталкиваемся с геометрическим определением вероятности такого события:

$P(B)=\frac{s}{S}$