Корреляция

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

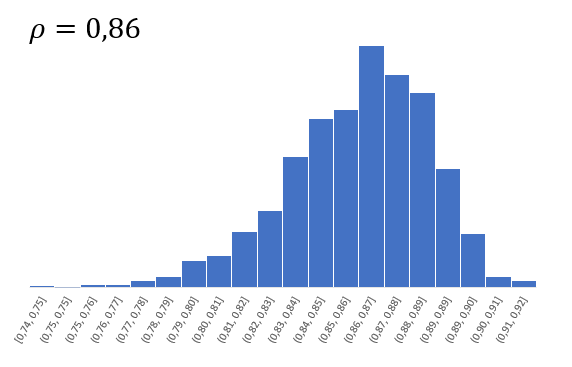
Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

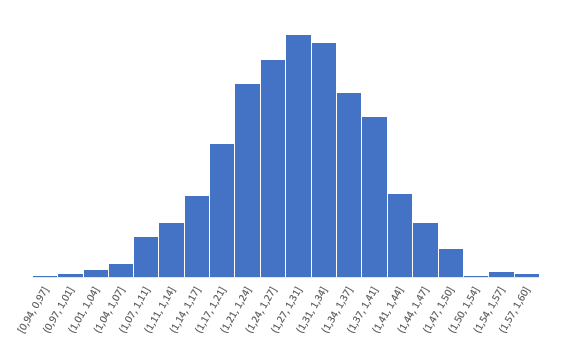
Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;N-1 – функция обратного стандартного распределения;γ – доверительная вероятность (часто 95%).Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Валютная корреляция и некоррелированные пары

Валютная корреляция на Форексе — это положительная или отрицательная связь между двумя валютными парами. Положительная корреляция означает, что две валютные пары движутся вместе, а отрицательная корреляция означает, что пары движутся в противоположных направлениях. Сам термин корреляция означает, что валютные пары имитируют друг друга.

Соотношение валютных пар играет важную роль в построении эффективной стратегии. При работе с высококоррелированными парами трейдеры обычно стремятся удвоить свою прибыль. Однако существуют некоррелированные валютные пары, которые обычно двигаются в противоречии друг с другом. Почему эти некоррелированные пары Форекс заслуживают внимания трейдеров?

Что же делать

То, что сработало для других, не обязательно сработает для вас.

• Если уйдёте из университета, не факт, что создадите Apple.

• Если перепишете туториал, не обязательно увеличите доход.

• Если добавите в название игры слова world, clash, go, это не гарантирует, что игра станет хитом.

Если вы обнаружили связь между двумя показателями, рекомендуем разобраться в деталях: что от чего зависит, что на что влияет (и влияет ли вообще). Из таких взаимосвязей и строится понимание предметной области, её модель в вашей голове.

Если другой продукт провёл A/Б-тест и выяснил, что у красной кнопки больший CTR, чем у зелёной, это не значит, что вам нужно сломя голову менять все кнопки на красные.

Если вы приняли участие в выставке, и после этого приток новых пользователей увеличился на 30%, не спешите подавать заявку на следующую выставку. Лучше детально разобраться в причинах — быть может, дело в сезонности.

Понимание дисперсии

При изучении корреляции важно понимать дисперсию, которая относится к степени, в которой набор данных распределяется или распределяется.Понимание дисперсии является ключом к пониманию корреляции, поскольку оно может сильно повлиять на взаимосвязь между двумя переменными.Дисперсия может быть измерена с использованием различных статистических инструментов, таких как диапазон, дисперсия и стандартное отклонение, каждый из которых предоставляет различные уровни информации о распределении точек данных. С математической точки зрения дисперсия измеряется объемом изменчивости в наборе данных.На эту изменчивость может повлиять многие факторы, такие как выбросы, размер выборки и основное распределение данных.Выбросы — это точки данных, которые значительно отличаются от остальных данных и могут значительно повлиять на дисперсию данных.Размер выборки также может влиять на дисперсию, так как большие размеры выборки имеют тенденцию иметь меньшую изменчивость, чем меньшие размеры выборки.Основное распределение данных также может влиять на дисперсию, причем различные распределения приводят к различным уровням изменчивости. С математической точки зрения дисперсия измеряется объемом изменчивости в наборе данных.На эту изменчивость может повлиять многие факторы, такие как выбросы, размер выборки и основное распределение данных.Выбросы — это точки данных, которые значительно отличаются от остальных данных и могут значительно повлиять на дисперсию данных.Размер выборки также может влиять на дисперсию, так как большие размеры выборки имеют тенденцию иметь меньшую изменчивость, чем меньшие размеры выборки.Основное распределение данных также может влиять на дисперсию, причем различные распределения приводят к различным уровням изменчивости

С математической точки зрения дисперсия измеряется объемом изменчивости в наборе данных.На эту изменчивость может повлиять многие факторы, такие как выбросы, размер выборки и основное распределение данных.Выбросы — это точки данных, которые значительно отличаются от остальных данных и могут значительно повлиять на дисперсию данных.Размер выборки также может влиять на дисперсию, так как большие размеры выборки имеют тенденцию иметь меньшую изменчивость, чем меньшие размеры выборки.Основное распределение данных также может влиять на дисперсию, причем различные распределения приводят к различным уровням изменчивости.

Чтобы лучше понять дисперсию, вот несколько ключевых концепций, которые следует иметь в виду:

1. Диапазон: диапазон измеряет разницу между самыми большими и наименьшими значениями в наборе данных.Несмотря на то, что он обеспечивает простой способ измерения дисперсии, на него могут сильно повлиять выбросы и могут не предоставить полную картину распределения данных.

2. Дисперсия: дисперсия измеряет, насколько распространены данные из среднего значения.Он учитывает все точки данных и обеспечивает более надежную меру дисперсии, чем диапазон.Тем не менее, это трудно интерпретировать, как это измеряется в квадратных единицах.

3. Стандартное отклонение: стандартное отклонение — это квадратный корень дисперсии и обеспечивает более интерпретируемую меру дисперсии.Он измеряет, насколько далеко точки данных находятся от среднего и часто используются для выявления выбросов или необычных точек данных.

Чтобы проиллюстрировать влияние дисперсии на корреляцию, рассмотрите следующий пример: предположим, что мы изучаем взаимосвязь между часами изучения и оценками экзаменов.Если данные сильно диспергированы, а некоторые студенты изучают очень мало, а другие много изучают, корреляция между часами обучения и оценками экзаменов может быть слабее, чем если бы данные менее рассеяны, причем большинство учащихся изучают аналогичное количество.Другими словами, дисперсия может повлиять на силу и направление взаимосвязи между двумя переменными и должна учитываться при интерпретации результатов корреляции.

Понимание дисперсии является ключевым компонентом изучения корреляции.Измеряя изменчивость точек данных, мы можем получить представление о распределении данных и о том, как это влияет на взаимосвязь между двумя переменными.Тщательное понимание дисперсии может помочь исследователям идентифицировать выбросы, интерпретировать результаты корреляции и сделать более осознанные выводы о данных.

Понимание дисперсии — Корреляция: Дисперсия и зависимость: исследование корреляции

Примеры

Необходимо определить взаимосвязь двух переменных: уровня интеллектуального развития (по данным проведенного тестирования) и количества опозданий за месяц (по данным записей в учебном журнале) у школьников.

Исходные данные представлены в таблице:

Чтобы дать правильную интерпретацию полученному показателю, необходимо проанализировать знак коэффициента корреляции (+ или -) и его абсолютное значение (по модулю).

В соответствии с таблицей классификации коэффициента корреляции по силе делаем вывод о том, rxy = -0,827 – это сильная отрицательная корреляционная зависимость. Таким образом, количество опозданий школьников имеет очень сильную зависимость от их уровня интеллектуального развития. Можно сказать, что ученики с высоким уровнем IQ опаздывают реже на занятия, чем ученики с низким IQ.

Важно! Принято считать, что чем r ближе по модулю к 1, тем ближе связь между анализируемыми переменными к линейной. Если величина r близка к -1, то связь обратная (c возрастанием переменной х переменная у убывает).. Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам

Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность

Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам. Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность.

Корреляционный анализ применяется в следующих областях:

• экономическая наука;
• астрофизика;
• социальные науки (социология, психология, педагогика);
• агрохимия;
• металловедение;
• промышленность (для контроля качества);
• гидробиология;
• биометрия и т.д.

Причины популярности метода корреляционного анализа:

1. Относительная простота расчета коэффициентов корреляции, для этого не нужно специальное математическое образование.
2. Позволяет рассчитать взаимосвязи между массовыми случайными величинами, которые являются предметом анализа статистической науки. В связи с этим этот метод получил широкое распространение в области статистических исследований.

Когда переменные не коррелированы: примеры

В статистике понятие корреляции используется для измерения связи между двумя переменными. Однако, в некоторых случаях переменные могут быть не коррелированы, т.е. не иметь значимой связи друг с другом. В этом разделе рассмотрим несколько примеров, когда переменные не коррелированы.

1. Пример 1: Рост и вес

Предположим, у нас есть данные о росте и весе разных людей. Если провести корреляционный анализ для этих данных, с большой вероятностью получим результат, который показывает отсутствие значимой связи между этими переменными. В данном случае можно сказать, что рост и вес не коррелируют друг с другом.

Пример 2: Уровень образования и доход

Еще одним примером может служить изучение взаимосвязи между уровнем образования и доходом

При анализе данных мы можем обнаружить, что уровень образования не имеет важного влияния на доход, и следовательно, эти переменные не коррелируют

Пример 3: Время обучения и успех в учебе

Допустим, мы исследуем связь между временем, затраченным на подготовку к экзамену, и успехом в учебе. Если провести статистический анализ, мы можем прийти к выводу, что эти две переменные не коррелируют друг с другом, то есть время обучения не оказывает значимого влияния на успех в учебе.

Это лишь некоторые примеры, когда переменные не коррелируют

В реальной жизни ситуации могут быть разными, и важно провести анализ для конкретных данных, чтобы понять наличие или отсутствие корреляции

Коэффициент корреляции Спирмена

В статистике также существует коэффициент корреляции Спирмена, который назван в честь статистика Чарльза Эдварда Спирмена (Spearman).

Цель этого коэффициента заключается в измерении интенсивности соотношения между двумя переменными, независимо от того, являются ли они линейными или нет.

Корреляция Спирмена служит для оценки того, может ли интенсивность взаимосвязи между двумя анализируемыми переменными быть измерена монотонной функцией (математическая функция, которая сохраняет или инвертирует соотношение начальной последовательности).

Как считать коэффициент корреляции Спирмена

Расчет коэффициента корреляции Спирмена уже немного отличается от предыдущей. Для этого необходимо организовать имеющиеся данные в следующую таблицу.

1. У вас должны быть две пары данных, соответствующих друг другу. Вы должны внести их в эту таблицу. Например, дирекция ресторана хочет узнать, есть ли связь между количеством заказов бутылок воды и количеством заказов десертов. Директор взял наугад данные 4-х столиков. Таким образом, у него получились две пары данных: где “Data А” — это заказы десертов, а “Data B” — заказы воды (т. е. первый столик заказал 7 десертов и 8 бутылок воды, второй — 6 десертов и 3 бутылки с водой и т. д.):

2. В столбце «Ranking А» мы будем классифицировать наблюдения, которые находятся в «Data А», нарастающим образом: «1» является самым низким значением в столбце и n (общее количество наблюдений) — самым высоким значением в столбце «Data А». В нашем примере это:

3. Сделайте то же самое позиционирование (классификацию наблюдений) для второго столбца “Data B”, записав это в столбце “Ranking B”.

4. В столбце «d» посчитайте разницу между двумя последними столбцами-ранкингами (A — B). Знак здесь учитывать не нужно (в следующем шаге узнаете почему).

5. Возведите во вторую степень каждое из значений, полученное в столбце «d».

6. Сделайте сумму всех данных, которые у вас получились в столбце «d2». Это будет Σd². В нашем примере Σd² = 0+1+0+1 = 2.

7. Теперь используем формулу Спирмена.

В нашем случае n = 4, мы это видим по количеству пар данных (соответствует числу наблюдений).

8. И наконец, замените данные в формуле.

Наш результат равен 0,8 или 80 %. Это означает, что переменные имеют положительную корреляцию.

Т. е. заказы бутылок воды и заказы десертов клиентами этого ресторана зависят друг от друга (т. к. коэффициент 0,8 далёк от 0), но не полностью (т. к. коэффициент очень близок к 1, но не равен 1). А положительная, так как коэффициент больше чем 0, это означает, что количество воды и количество десертов увеличиваются вместе, а не наоборот (т. е. чем выше количество потребляемой воды, тем выше количество потребляемых десертов).

Смещение

Аналогично тому, как производится выборка из генеральной совокупности, дата-сайентисты из готового датасета выделяют тренировочный набор. Именно на этой «выборке второго порядка» модель учится делать предсказания.

Прочитайте нашу статью о создании простой модели машинного обучения. Она предсказывает город, в который вероятнее всего поедет турист, на основании его возраста, пола, места жительства, дохода и транспортных предпочтений. Такая рекомендательная система на минималках.

Смещение происходит, когда модель недооценивает или переоценивает какой-либо параметр. Представим, что модель из статьи выше отправляет всех краснодарцев в Париж — независимо от их дохода, предпочтений и других параметров. В этом случае мы скажем, что модель переоценивает значение параметра «Город проживания».

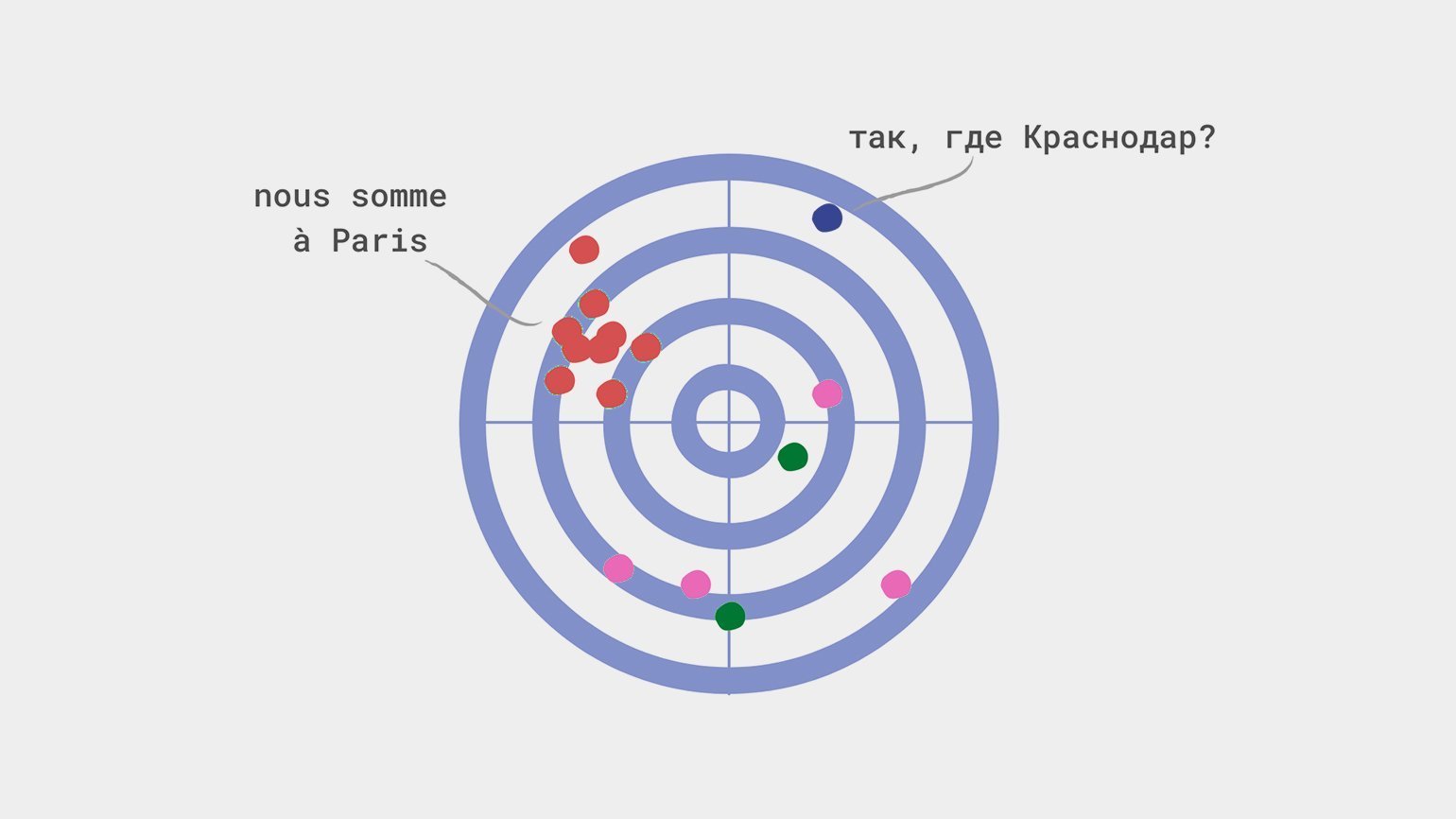
Чаще всего причиной смещения являются:

• неправильный сбор данных в датасет: например, в него попали только краснодарцы — любители Парижа;
• неправильное формирование тренировочного набора из датасета;
• неправильное измерение ошибок.

Когда мы неверно собираем данные, говорят о систематической ошибке отбора. Например, в прошлом веке многие считали, что во Вселенной больше голубых галактик, — впечатление возникало потому, что плёнка была более чувствительна к голубой части спектра.

О доброте дельфинов мы знаем только от спасённых ими людей. Фото: Pixabay

Другая ошибка — ошибка меткого стрелка — происходит, когда мы вольно или невольно отбираем в выборку только схожие между собой данные, то есть фактически рисуем мишень вокруг места, куда попадём.

Причин, вызывающих смещение, так много, что Марк Твен заметил: «Существует три вида лжи: ложь, наглая ложь и статистика». Например:

• Эффект низкой/высокой базы. Если в финансовом отчёте найти самый низкий показатель прибыли, то на его фоне любой другой результат будет выглядеть как достижение. И наоборот: если хотите показать, что ученик перестал прогрессировать, сравнивайте текущие оценки с его лучшими результатами за все годы обучения.
• Сокращение рассматриваемого периода. Если хочется доказать, что рекламная кампания не приносит результатов, надо просто найти период, когда деньги уже потрачены, а эффекта ещё нет. И рассматривать только его.
• Исключение из выборки. Если вы измеряете результативность методики снижения веса, то можно выкидывать из выборки участников, которые отказались от методики, не дойдя до конца. Это существенно «повысит» эффективность методики.
• Ну и, конечно же, классика: «Интернет-опрос населения показал, что 100% населения пользуются интернетом».

Эти и другие ошибки смещения трудно выявить статистическими методами, поэтому нужно стараться избежать их до того, как вы начнёте сбор данных.

Если пить «Боржоми» уже поздно (датасет уже сформирован), обязательно спросите себя: «Не смещены ли мои данные?» — а они наверняка смещены, «Куда и почему они смещены?» и «Можно ли с этим жить?»

Понятие корреляции

Корреляция (от латинского «correlatio» – соотношение, взаимосвязь) – математический термин, который означает меру статистической вероятностной зависимости между случайными величинами (переменными).

Пример: возьмем два вида взаимосвязи:

1. Первый – ручка в руке человека. В какую сторону движется рука, в такую сторону и ручка. Если рука находится в состоянии покоя, то и ручка не будет писать. Если человек чуть сильнее надавит на нее, то след на бумаге будет насыщеннее. Такой вид взаимосвязи отражает жесткую зависимость и не является корреляционным. Это взаимосвязь – функциональная.
2. Второй вид – зависимость между уровнем образования человека и прочтением литературы. Заранее неизвестно, кто из людей больше читает: с высшим образованием или без него. Эта связь – случайная или стохастическая, ее изучает статистическая наука, которая занимается исключительно массовыми явлениями. Если статистический расчет позволит доказать корреляционную связь между уровнем образованности и прочтением литературы, то это даст возможность делать какие-либо прогнозы, предсказывать вероятностное наступление событий. В этом примере с большой долей вероятности можно утверждать, что больше читают книги люди с высшим образованием, те, кто более образован. Но поскольку связь между данными параметрами не функциональная, то мы можем и ошибиться. Всегда можно рассчитать вероятность такой ошибки, которая будет однозначно невелика и называется уровнем статистической значимости (p).

Примерами взаимосвязи между природными явлениями являются: цепочка питания в природе, организм человека, который состоит из систем органов, взаимосвязанных между собой и функционирующих как единое целое.

Каждый день мы сталкиваемся с корреляционной зависимостью в повседневной жизни: между погодой и хорошим настроением, правильной формулировкой целей и их достижением, положительным настроем и везением, ощущением счастья и финансовым благополучием. Но мы ищем связи, опираясь не на математические расчеты, а на мифы, интуицию, суеверия, досужие домыслы. Эти явления очень сложно перевести на математический язык, выразить в цифрах, измерить. Другое дело, когда мы анализируем явления, которые можно просчитать, представить в виде цифр. В таком случае мы можем определить корреляцию с помощью коэффициента корреляции (r), отражающего силу, степень, тесноту и направление корреляционной связи между случайными переменными.

Сильная корреляция между случайными величинами – свидетельство наличия некоторой статистической связи конкретно между этими явлениями, но эта связь не может переноситься на эти же явления, но для другой ситуации. Часто исследователи, получив в расчетах значительную корреляцию между двумя переменными, основываясь на простоте корреляционного анализа, делают ложные интуитивные предположения о существовании причинно-следственных взаимосвязей между признаками, забывая о том, что коэффициент корреляции носит вероятностный характер.

Пример: количество травмированных во время гололеда и число ДТП среди автотранспорта. Эти величины будут коррелировать между собой, хотя они абсолютно не взаимосвязаны между собой, а имеют только связь с общей причиной этих случайных событий – гололедицей. Если же анализ не выявил корреляционной взаимосвязи между явлениями, это еще не является свидетельством отсутствия зависимости между ними, которая может быть сложной нелинейной, не выявляющейся с помощью корреляционных расчетов.

Первым, кто ввел в научный оборот понятие корреляции, был французский палеонтолог Жорж Кювье. Он в XVIII веке вывел закон корреляции частей и органов живых организмов, благодаря которому появилась возможность восстанавливать по найденным частям тела (останкам) облик всего ископаемого существа, животного. В статистике термин корреляции впервые применил в 1886 году английский ученый Френсис Гальтон. Но он не смог вывести точную формулу для расчета коэффициента корреляции, но это сделал его студент – известнейший математик и биолог Карл Пирсон.

Меры описательной статистики

Задача описательной статистики, как следует из названия, — дать хорошее описание данных. Она не для предсказаний, выводов или преобразований — только внешняя форма данных, измеренная в показателях.

Ключевые показатели, применяемые в описательной статистике (их ещё называют мерами или, если точнее, ), — это:

• Среднее: чаще всего вычисляется как среднее арифметическое. Просто складываем все значения, делим на их количество — и вуаля, средняя температура по больнице готова.
• Медиана: если выстроить все данные по возрастанию и найти середину этого ряда, это как раз и будет медиана. Одна половина из значений данных будет больше медианы, а другая — меньше.
• Мода: значение в наборе данных, которое встречается чаще всего. Запомнить очень легко: мода — самое популярное из значений, то, что «носят все».

Посмотрите это небольшое видео о среднем, медиане и моде на сайте Академии Хана — образовательного ресурса, который славится доходчивыми объяснениями. Там всё просто, на понятном русском языке.

Кроме трёх перечисленных, есть и другие статистические показатели — например, . Главная из них — дисперсия, о ней ниже. Все они нужны, чтобы понять, какие перед нами данные и о чём именно они рассказывают.

Остатки

К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:

Здесь, ε  — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:

Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).

Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.

Обычные наименьшие квадраты

Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.

Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.

Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:

Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:

Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:

Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.

Корреляционный анализ[править | править код]

Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).

Ограничения корреляционного анализа

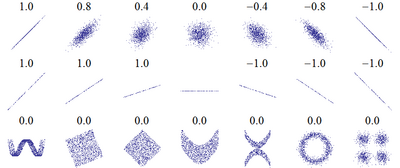
Множество корреляционных полей. Распределения значений (x,y){\displaystyle (x,y)} с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.

1. Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.
2. Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения.
3. Исходная совокупность значений должна быть качественно однородной.
4. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.

Область применения

Данный метод обработки статистических данных весьма популярен в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.

Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Семплирование

Предположим, вам требуется решить важную задачу: выяснить среднюю ширину морды домашних котов нашей страны. Прямой способ, то есть измерение всех домашних питомцев, невозможен по ряду объективных причин. Придётся ограничиться выборкой — взять какое-то число животных, измерить морды именно им и сделать выводы по итогам только этих исследований.

Иллюстрация: Pixabay

Но тут сразу же возникают вопросы:

• Сколько и каких котов отобрать для замера?
• Почему именно этих, а не других?
• Какие есть гарантии, что вычисленное значение действительно будет средней шириной морды всех котов России?

Семплирование — это группа статистических методов и приёмов, отвечающих на эти вопросы. С помощью семплирования мы формируем нашу выборку так, чтобы она наилучшим образом отражала свойства генеральной совокупности — то есть свойства всех котов страны.

Качественная выборка сохраняет свойства всей генеральной совокупности

Иными словами, вы не можете измерить N первых попавшихся котов и обобщить результат для остальных. Выборка должна хорошо «сидеть» во всей популяции кошек, чтобы можно было делать обоснованные выводы. Такую выборку называют релевантной.

Кстати, статистика и котики — близнецы-братья. После выхода одноимённой книги Владимира Савельева мы говорим «статистика», а подразумеваем «котики», и наоборот. И смело рекомендуем эту книгу всем, кто дочитал до этого места.

В Data Science методы семплирования применяются при разработке, подготовке и оценке датасетов, чтобы они одновременно и были упорядоченными, и соответствовали реальности.