Введение
В информатике, теория сложности вычислений является разделом теории вычислений, изучающим стоимость работы, требуемой для решения вычислительной проблемы. Стоимость обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством тривиальных шагов, необходимых для решения проблемы, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа и выхода?».
Значение коэффициента сложности для заказчика
При планировании и оценке работ по монтажу очень важно учитывать коэффициент сложности выполнения. Он позволяет определить степень трудоемкости задач и соответственно оценить необходимые ресурсы и время. Коэффициент сложности является фактором, который влияет на стоимость и качество работ
Он определяет ориентировочную сложность проекта и включает в себя такие факторы, как:
Коэффициент сложности является фактором, который влияет на стоимость и качество работ. Он определяет ориентировочную сложность проекта и включает в себя такие факторы, как:
- Условия проведения работ. Это может быть ограниченное рабочее пространство, пропускные способности объекта, высокие требования к безопасности и т.д.
- Требуемые технические решения. В зависимости от уровня технических требований заказчика, могут быть необходимы специализированные навыки и оборудование.
- Сроки выполнения работ. Если требуется выполнить работы в кратчайшие сроки, это может потребовать дополнительных ресурсов и организационных усилий.
Заказчику важно быть осведомленным о значении коэффициента сложности, поскольку это позволяет оценить все риски и нюансы, связанные с выполнением работ. Например, при более высоком коэффициенте сложности заказчик может рассчитывать на высокий уровень профессионализма и качества работ, но при этом стоимость может быть выше, а сроки выполнения — дольше. Конечно, каждый заказчик имеет свои индивидуальные требования и ожидания от проекта, поэтому важно учесть все особенности и составить адекватную оценку сложности
Для этого рекомендуется обратиться к профессионалам своей отрасли или специалистам по монтажу, которые имеют опыт работы с подобными проектами
Конечно, каждый заказчик имеет свои индивидуальные требования и ожидания от проекта, поэтому важно учесть все особенности и составить адекватную оценку сложности. Для этого рекомендуется обратиться к профессионалам своей отрасли или специалистам по монтажу, которые имеют опыт работы с подобными проектами. В заключение, значение коэффициента сложности для заказчика заключается в возможности более точно планировать и управлять проектом, учитывая все факторы и требования, а также принимать взвешенные решения в отношении стоимости, сроков и качества работ
В заключение, значение коэффициента сложности для заказчика заключается в возможности более точно планировать и управлять проектом, учитывая все факторы и требования, а также принимать взвешенные решения в отношении стоимости, сроков и качества работ.
Задачка от Google
Возьмём для нашего финального оценивания задачку, которую дают на собеседовании в Google.
Подробный разбор задачи и алгоритмы решения можно посмотреть вот в этом видео от Саши Лукина. Рекомендую посмотреть его перед тем, как продолжить читать эту статью.
Вкратце, цель алгоритма — найти в массиве два любых числа, которые в сумме дали бы нам искомое число target.
Решение 1: полный проход по массиву
Сложность по времени: O(n^2)
Сложность по памяти: O(С)
Это решение в лоб. Не самое оптимальное, поскольку время быстро растёт при увеличении количества элементов, но зато дополнительную память мы особо не потребляем.
Решение 2: используем HashSet
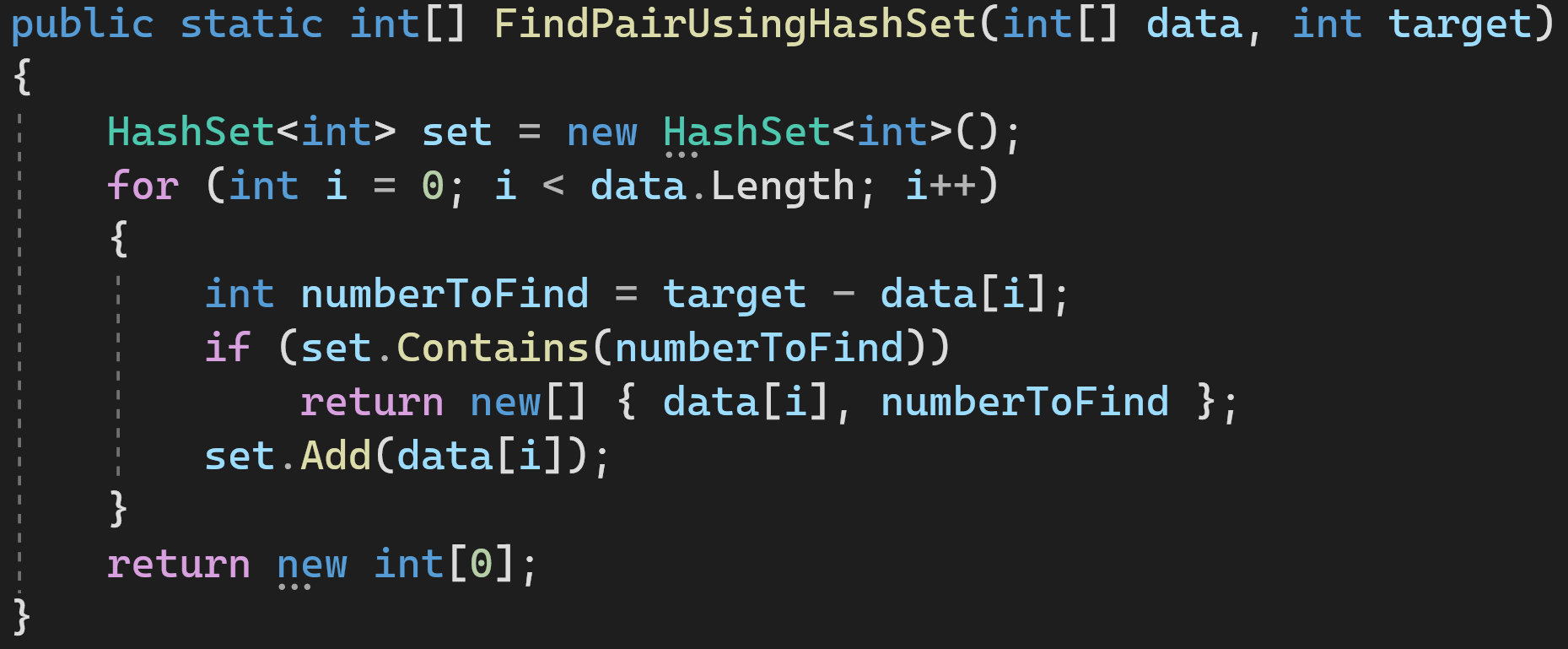
Проходимся по массиву и добавляем элементы, которые мы уже проверили, в HashSet. Если HashSet содержит недостающий для суммы элемент, значит всё хорошо, мы закончили и можем возвращать результат.
Сложность по времени: O(n)
Сложность по памяти: O(n)
Это как раз пример того, как можно выиграть в производительности, выделив дополнительную память для промежуточных структур.
Решение 3: используем бинарный поиск
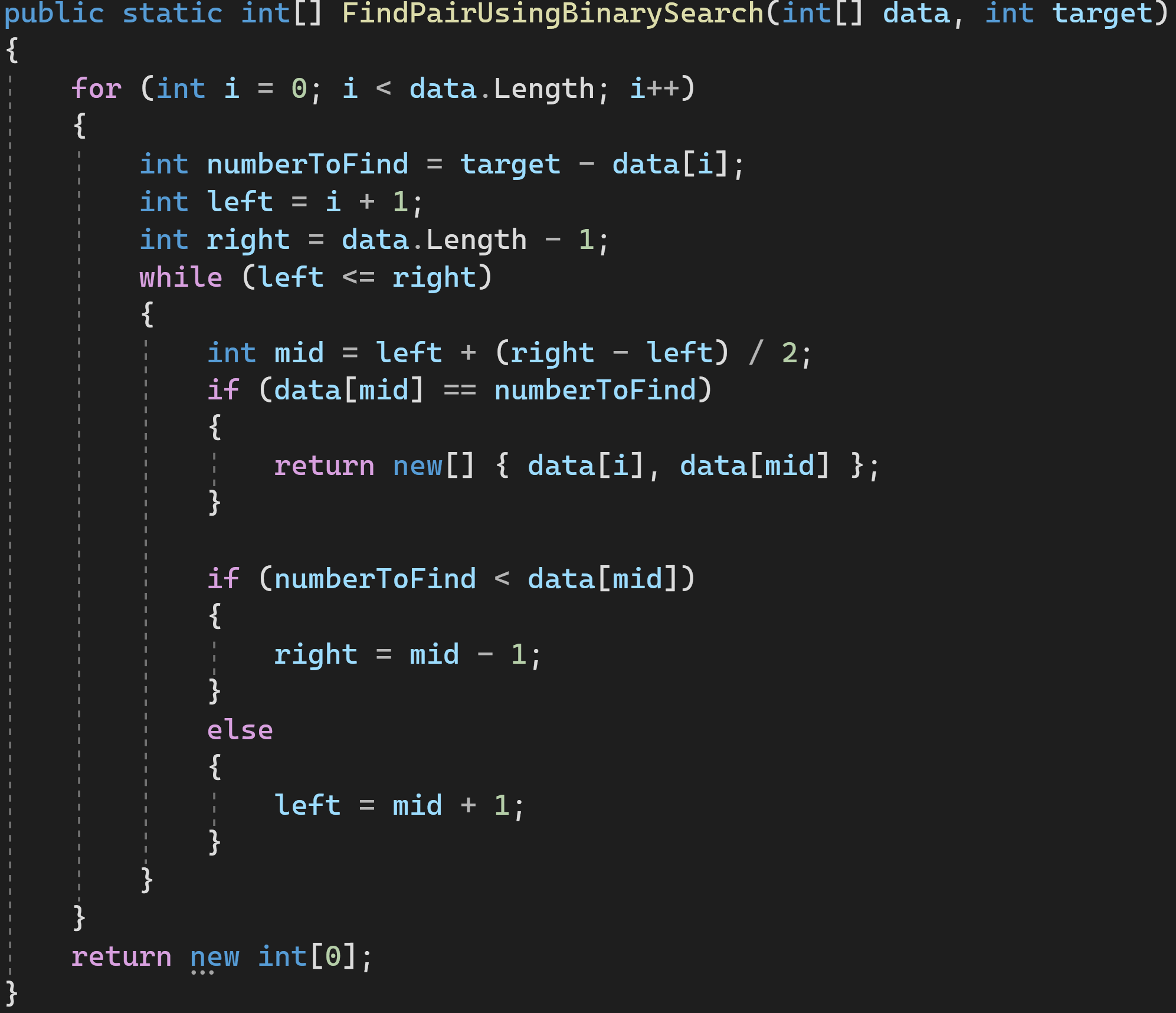
Алгоритм бинарного поиска имеет известную сложность — O(log(n)). O(n) нам добавилась от внешнего цикла for, а всё, что внутри цикла while — это и есть алгоритм бинарного поиска. Согласно Правилу 4 сложности перемножаются.
Сложность по времени: O(n*log(n))
Сложность по памяти: O(С)
Решение 4: используем метод двух указателей
Двигаем левый и правый указатели к центру, пока они не сойдутся или не найдется пара подходящих нам значений.
Сложность по времени: O(n)
Сложность по памяти: O(С)
И это — самый оптимальный из всех вариантов решения, не использующий дополнительной памяти и совершающий наименьшее количество операций.
Коэффициент экономической сложности
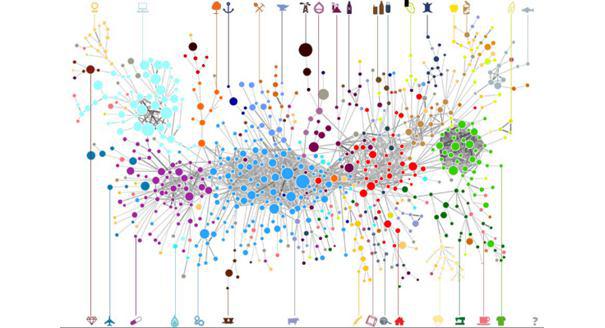
КЭС (ECI) — показатель, разработанный Рикардо Хаусманном и характеризующий сложность и диверсифицированность экспортируемых товаров страны. Для оценки экономической сложности используется статистика международной торговли. Учитываются те продукты, в производстве которых страна имеет устойчивое конкурентное преимущество, то есть экспортирует больше, чем средняя экономика подобного размера. Индекс сложности экономики отражает, насколько сложна совокупность производимой страной продукции.
Каждая цветная точка на картинках — это отрасль промышленности, участвующая в мировой торговле. Справа налево и от периферии к центру сложность продуктов постепенно увеличивается. Выделяются несколько крупных кластеров: легкой промышленности (зеленый), машиностроения (синий), электроники (бирюзовый), химии и фармацевтики (фиолетовый), сельского хозяйства (желтый). Расстояние между точками отражает простоту освоения одной технологии при наличии другой.
Существует устойчивая корреляция уровня ВВП на душу населения и индекса экономической сложности. Чем сложнее экономика, тем страна богаче. Специализация на простых технологиях не позволяет достичь устойчивого высокого уровня благосостояния. Исключение составляют только нефтедобывающие страны в период высоких цен на нефть.
Визуализации данных по всем странам можно посмотреть тут: http://atlas.cid.harvard.edu
Вся мировая экономика (2014):
Германия, ECI = 1,92, вторая в мире по уровню сложности:
Исследования VQ
Термин VQ впервые ввел французский психолог Пьер Касс. По его мнению, объем жизненной энергии – главная движущая сила и стимулятор человека.
Он полагал, что именно этот коэффициент определяет стремление реализовать возможности, чтобы воплотить в реальность главную стратегию.
Но мысль о разных видах интеллекта допускалась и до работы Пьера Касса. Так, в 1983 году психолог Говард Гарднер ввел понятие «множественный интеллект», которое включает в себя следующие типы:
- телесно-кинетический;
- языковой (лингвистический);
- логико-математический;
- натуралистический;
- внутриличностный;
- межличностный;
- пространственный;
- музыкальный.
Психолог утверждал, что каждый человек обладает одним или двумя основными типами интеллекта, но при желании вполне может развить способности и в других направлениях.
Пример
Ваша задача — обеспечить быстрый и удобный поиск для пользователей.
Если вы не учтете сложность алгоритмов, то при реализации поиска вы можете выбрать неоптимальный алгоритм, который будет медленно обрабатывать запросы пользователей при большом количестве товаров. Например, вы можете реализовать поиск, который каждый раз просматривает все товары и сравнивает их с запросом пользователя.
Однако, если вы знаете сложность алгоритмов, то сможете выбрать более эффективный алгоритм для поиска, такой как бинарный поиск или хэш-таблицы. Эти алгоритмы имеют лучшую производительность и работают намного быстрее, даже если у вас есть большой каталог товаров.
Определение факторов сложности
| Фактор | Описание |
|---|---|
| Объем работы | Количество задач или объем данных, с которыми необходимо работать. Чем больше объем работы, тем выше сложность задания. |
| Техническая сложность | Сложность в реализации технической стороны проекта, задачи или задания. Включает в себя уровень технической экспертизы, необходимой для успешного выполнения. |
| Временные ограничения | Наличие сроков выполнения задачи или проекта. Чем меньше времени на выполнение, тем выше сложность. |
| Зависимости | Наличие взаимосвязей или зависимостей между задачами, проектами или заданиями. Чем сложнее зависимости, тем выше сложность. |
| Неопределенность | Степень предсказуемости или неопределенности в выполнении задачи или проекта. Чем больше неопределенности, тем выше сложность. |
| Изменчивость требований | Частота и степень изменения требований или спецификации проекта или задачи. Чем чаще и существеннее изменяются требования, тем выше сложность. |
| Навыки и опыт исполнителя | Уровень знания, навыков и опыта у исполнителя задачи. Чем выше требуется уровень квалификации, тем выше сложность. |
Определение факторов сложности позволяет получить объективную оценку сложности задачи или проекта, что в свою очередь обеспечивает более точное измерение коэффициента сложности.
Цикломатические меры сложности
Каждая программа включает в себя операторы, которые нужно выполнить для выполнения некоторых задач, и другие операторы принятия решений, которые определяют, какие операторы необходимо выполнить. Эти конструкции принятия решений изменяют ход программы.
Если мы сравним две программы одинакового размера, то программа с большим количеством операторов принятия решений будет более сложной, поскольку управление программой часто переключается.
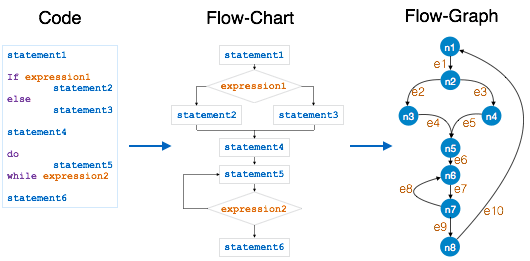
МакКейб в 1976 году предложил Cyclomatic Complexity Measure для количественной оценки сложности данного программного обеспечения. Это модель на основе графов, основанная на конструкциях программы для принятия решений, таких как операторы if-else, do-while, repeat-until, switch-case и goto.
Процесс построения графика управления потоком:
- Разбейте программу на более мелкие блоки, разграниченные конструкциями принятия решений.
- Создайте узлы, представляющие каждый из этих узлов.
- Подключите узлы следующим образом:
-
Если управление может перейти от блока i к блоку j
Нарисуйте дугу
-
От узла выхода к узлу входа
Нарисуйте дугу.
-
Для расчета цикломатической сложности программного модуля мы используем формулу —
Цикломатическая сложность указанного выше модуля равна
По словам П. Йоргенсена, цикломатическая сложность модуля не должна превышать 10.
Коэффициент на работы, осуществляемые в стесненных условиях производства работ
Коэффициент компенсирует трудности, связанные с работой в ограниченном пространстве или рядом с другими объектами: ограниченное движение рабочих или невозможность использования некоторых видов оборудования и инструментов. Например, при строительстве административного здания в плотной городской застройке.
Коэффициент равен 1,15, но чтобы его применить необходимо наличие минимум трех из перечисленных факторов:
-
интенсивное движение городского транспорта и пешеходов в пределах 50 м от зоны производства работ;
-
наличие сетей подземных коммуникаций, подлежащие перекладке или подвеске;
-
расположение объектов капитального строительства и сохраняемых зеленых насаждений в пределах 50 м от зоны производства работ;
-
стесненные условия или невозможность складирования материалов;
-
ограничение поворота стрелы грузоподъемного крана в соответствии с данными проекта организации строительства.
Все эти требования прописаны в п. 53.1 Приказа Минстроя РФ № 421/пр.
В чем сложность применения коэффициента. С двумя факторами — интенсивное движение пешеходов и ограничение поворота стрелы крана — проблем не возникает. Сложнее всего найти и обосновать все три фактора.
Сети подземных коммуникаций, подлежащие перекладке, считаются проектными решениями. Если их перекладка учтена в другом проекте, то затраты на нее учитываются отдельно. Соответственно, этот фактор можно применить не во всех случаях.
Сохраняемые зеленые насаждения в непосредственной близости от зоны производства работ, как правило, тоже редко встречаются. На строительной площадке деревья, кустарники и прочую растительность убирают при проведении планировочных работ. Для обоснования данного фактора необходимо активное участие разработчика ПОС (проекта организации строительства) в соответствующих разделах ПЗУ (планировки земельного участка), ППО (проекта полосы отвода).
Чтобы доказать невозможность складирования материалов необходимо провести расчеты. Зачастую они показывают, что для выполняемых работ площадей складирования хватает. Фактор сложно обосновать, потому что он зависит от методики расчета. Поэтому за этим лучше обращаться к организациям, у которых есть опыт в таких сложных обоснованиях.
Наше решение. Найти для обоснования два фактора легко. С поиском и объяснением третьего факторы возникают сложности. Поэтому мы предлагаем различные варианты для его обоснования:
-
расчет необходимых площадей складирования для данной захватки;
-
использование чертежей, на которых мы показываем на графике ограничение поворота стрелы крана;
-
применение схемы перевалки материалов в тех ситуациях, где нет возможности сразу привезти материал на строительную площадку.
Мы в «Эрго Инжиниринг групп» не раз сталкивались с задачей найти третий фактор. Если у вас возникают сложности в обосновании коэффициентов, задайте вопрос нашему менеджеру. Мы проверим, можно ли применить коэффициент в вашем случае, и расскажем, как это сделать корректно. Это поможет вам сэкономить время и убережет от разногласий при согласовании сметы.
Немного практики:правила расчета сложности
Пример 1:
Возьмём для начала простой алгоритм присвоения переменной:
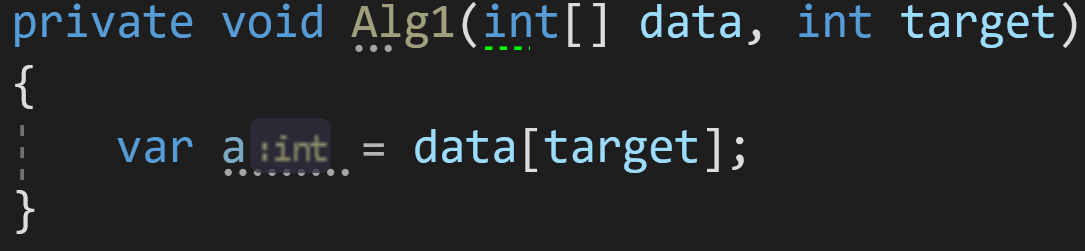
Какова его сложность по времени и по памяти?
С одной стороны, нас может ввести в заблуждение массив данных data неизвестной размерности. Но брать его в расчёт при оценке сложности внутреннего алгоритма будет некорректно.
Правило 1: внешние данные не учитываются в сложности алгоритма.
Получается, наш алгоритм состоит только из одной строчки: var a = data;
Доступ к элементу массива по индексу — известная операция со сложностью O(1) или O(C). Соответственно, и весь алгоритм по времени у нас займет O(1).
Дополнительная же память выделяется только под одну переменную. А значит, объём данных, которые мы будем передавать (хоть 1 000, хоть 10 000), не скажется на финальном результате. Соответственно, сложность по памяти у нас так же — O(1) или O(C).
Для упрощения записи дальше я везде буду писать O(C) вместо O(1), C в этом случае — это константа. Она может равняться 1, 2 или даже 100 — для современных компьютеров это число не принципиально, поскольку и 1, и 100 операций выполняются практически за одно и то же время.
Пример 2:
Рассмотрим второй алгоритм, очень похожий на первый:
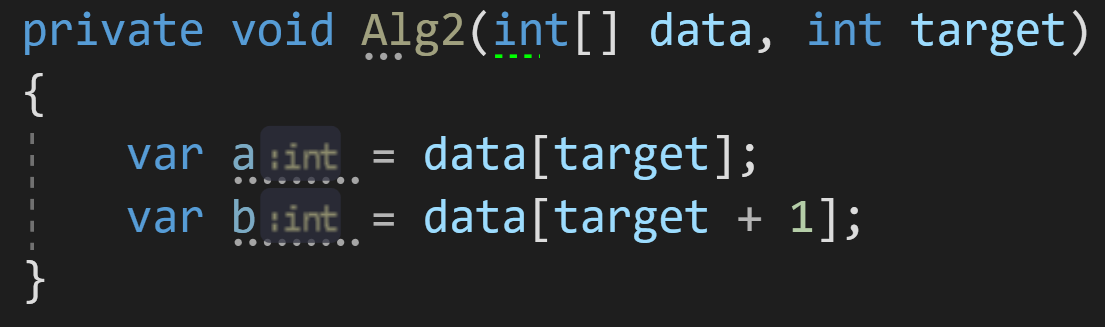
Влияет ли размерность входного массива data на количество операций в нём? Нет.
А на выделенную память? Тоже нет.
Сложность этого алгоритма по времени выполнения можно было бы оценить как O(2*C) — поскольку у нас выполняется в два раза больше операций, чем в предыдущем примере, 2 присваивания вместо 1. Но у нас и на этот счёт есть правило:
Правило 2: опускать константные множители, если они не влияют на результат кардинальным образом.
Если принять это правило в расчёт, сложность этого алгоритма будет такой же, как и в первом примере — O(C) по времени и O(C) по памяти.
Пример 3:
В третьем примере добавим в наш алгоритм цикл для обработки данных:
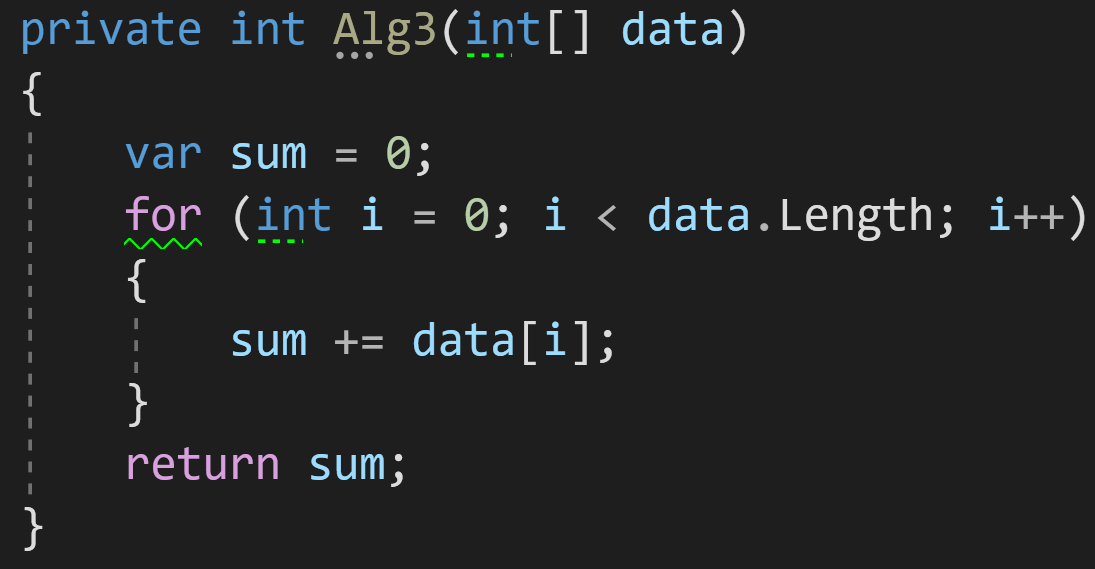
Как мы видим, количество операций, которые будет выполнять цикл, напрямую зависит от количества входных данных: больше элементов в data — больше циклов обработки потребуется для получения финального результата.
Казалось бы, если взять в учёт каждую строчку кода нашего алгоритма, то получилось бы что-то такое:
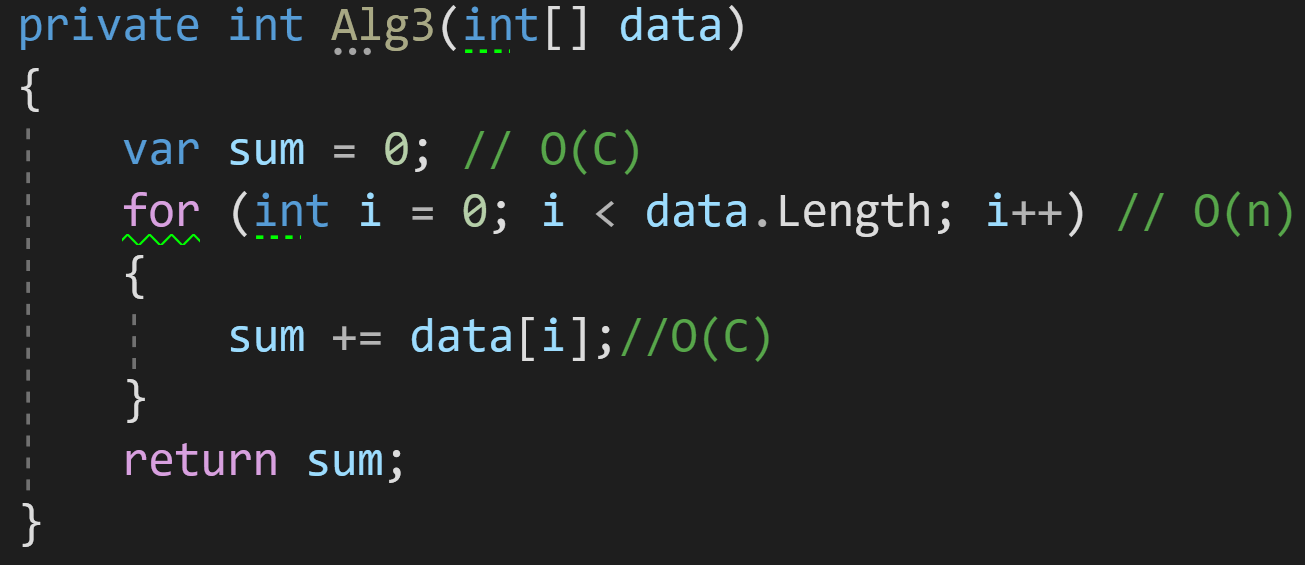
И тогда финальная сложность алгоритма получится O(C)+O(n). Но тут опять вмешивается новое правило:
Правило 3: опускать элементы оценки, которые меньше максимальной сложности алгоритма.
Поясню: если у вас O(C)+O(n), результирующая сложность будет O(n), поскольку O(n) будет расти всегда быстрее, чем O(C).
Еще один пример — O(n)+O(n^2). При такой сложности у нас N^2 всегда растёт быстрее, чем N, а значит O(n) мы отбрасываем и остаётся только O(n^2).
Итак, сложность нашего третьего примера — O(n).
Пример 4:
В четвёртом примере добавим на вход уже двумерный массив.
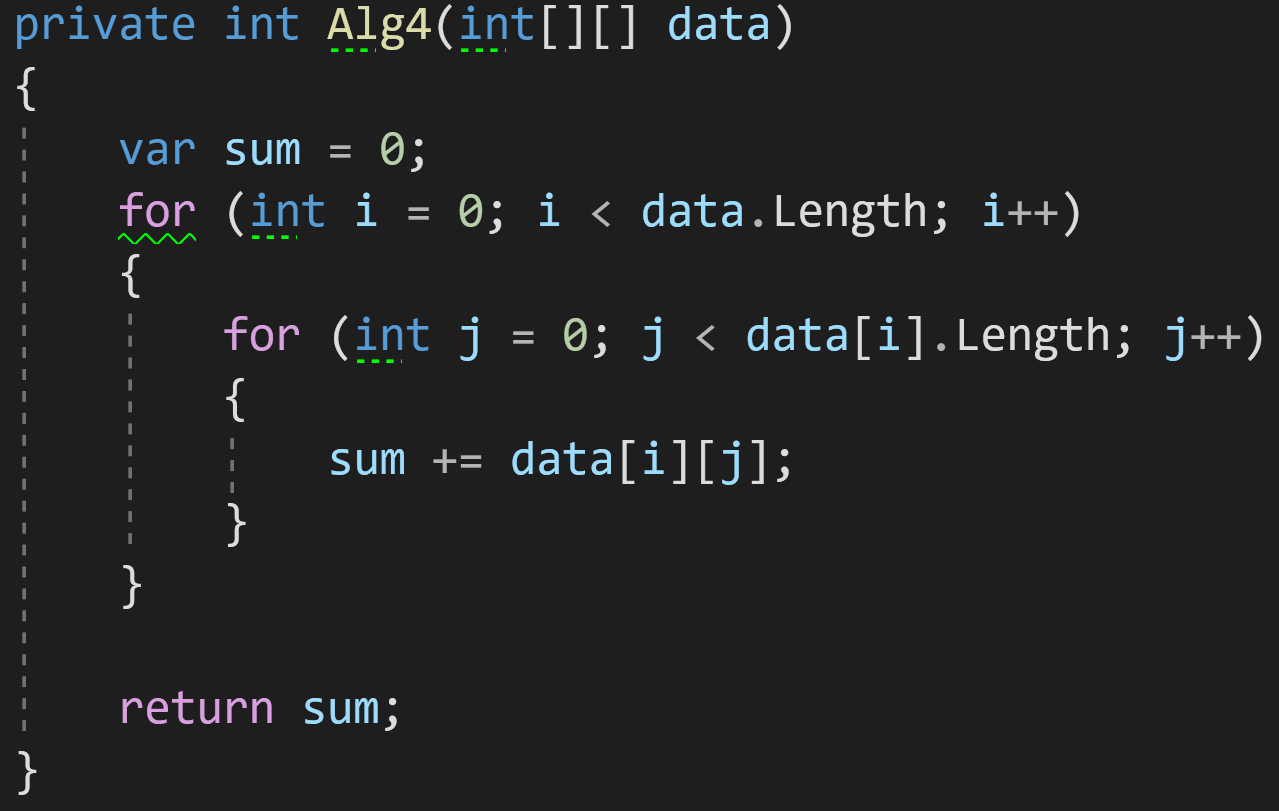
И для его обработки нам теперь нужно два цикла. Оба этих цикла будут зависеть от размерности входных данных data.
Правило 4: вложенные сложности перемножаются.
Сложность внешнего цикла в нашем примере — O(N), сложность внутреннего цикла — O(N) (или O(M), если массив не квадратный). Согласно правилу, две эти сложности должны быть умножены. В результате максимальная сложность всего алгоритма будет равна O(N^2).
Пример 5:
А что мы видим тут? Цикл — уже известная нам сложность O(n), но внутри вызывается функция Alg4() из предыдущего примера:
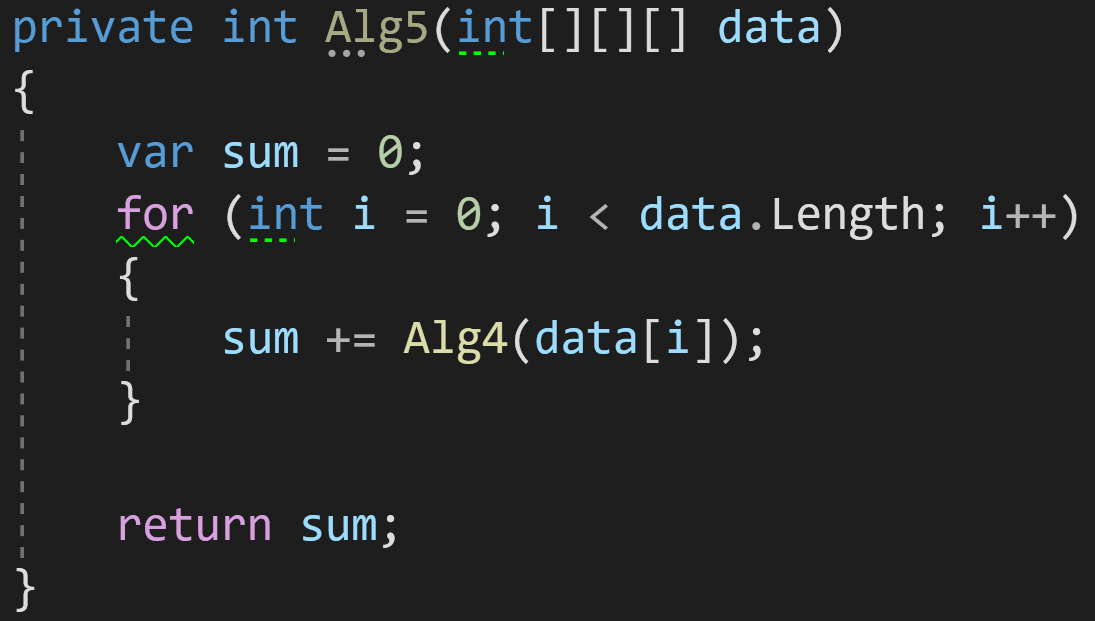
Если мы вспомним её сложность O(n^2), а также правило 4, то получим, что сложность этого алгоритма — O(n^3) при всей его визуальной минималистичности.
Правило 5: включайте в оценку общей сложности алгоритма оценки всех вложенных вызовов функций.
Именно поэтому важно понимать сложность методов синтаксического сахара вроде LINQ — чтоб была возможность оценить, как метод будет вести себя при увеличении объёмов данных. При использовании их в коде без понимания внутреннего устройства вы рискуете получить очень высокую сложность алгоритма, который будет захлебываться при увеличении входящих данных
Приведу пример минималистичного алгоритма, который выглядит хорошо и компактно (ни в коем случае не претендует на эталонный код), но станет бомбой замедленного действия при работе с большими объёмами данных:
Что мы тут видим? Цикл = O(n), Where = от O(1) до O(n), в зависимости от типа хранящихся внутри данных, Contains = O(n).
Итого сложность такого алгоритма будет от O(n^2) до O(n^3) по времени выполнения.
ToArray() будет выделять на каждой итерации дополнительную память под копию массива, а значит сложность по памяти составит O(n^2).
Среднее время жизни дефекта
Общее время, в течение которого были открытыми дефекты, найденные в рамках итерации или релиза к сумме дефектов.
Назначение метрики: показать, сколько в среднем времени уходит на работу с одним дефектом: на его регистрацию, исправление и воспроизведение. Данный показатель позволит оценить время, необходимое на тестирование, выделить области ПО с которыми возникают наибольшие сложности.
- Обычно время жизни дефекта, это все время от его создания (статус Created) до закрытия (Closed) за вычетом всех возможных Postponed и Hold. Любой баг-трекер позволяет рассчитать и выгрузить данную информацию для отдельного спринта или релиза.
- Также среднее время жизни дефекта можно рассчитывать для различных модулей и функций ПО, или, что самое интересное, отдельно для каждого из тестировщиков и разработчиков из команды. Так есть шанс выявить особенно сложные модули или слабое звено в команде ПО.
Группа 4 — Качество работы команды тестирования
Задача этого набора метрик оценить насколько качественно тестировщики выполняют свои задачи, определить уровень компетенций и зрелости команды QA. Обладая таким набором показателей можно сравнивать команду с ней же самой в разные моменты времени или с другими, внешними группами тестирования.
Альтернативные подходы
В конце 1970х была предложена концепция цикломатической сложности по Хольстеду, которая более детально учитывала имплементацию программы, и позволяла лучше оценить время на тестирование, вероятность ошибок, и общие затраты труда на создание и поддержку программы на любом Си-подобном языке. Хольстед предложил понимать любую компьютерную программу как «набор токенов», то есть операторов и операндов, и при подсчете времени тестирования учитывать количество уникальных операторов, их общее количество в программе, и формировалась итоговая метрика примерно так (и она получалась сложноватой, согласитесь):

Цикломатическая сложность по Маккейбу является развитием изложенной выше концепции, но с упором на точки принятия решений и графы (так называемая graph driven model). Маккейб предложил разбивать программу на блоки (каждый блок = точка принятия решений) и соединять их рёбрами по определенному принципу, и к стандартной схеме добавил граф:
Считается, что цикломатическая сложность в идеале не должна превышать 10. В гайдах по качеству кода, например Microsoft, особо подчеркивается, что высокая ЦС чревата ошибками (то есть багами). Анализаторы кода в IDE-редакторе отправляют разработчику (автоматическое) уведомление, если ЦС превысила пороговое значение (по дефолту 25, но можно настроить и ниже/выше).
В 2017 предложен совсем альтернативный подход к оценке сложности программного кода — с точки зрения его читаемости, то есть легкости восприятия человеком (что разумеется имеет значение и для QA тоже). В какой-то мере читаемость зависит от самого языка, например, код на HTML или SQL явно лучше читается человеком, чем на C++ или Java. При этом отличают необходимую сложность кода (которую никак нельзя устранить, из-за специфики языка, или специфики самой программы) и непреднамеренную, которая может и должна быть успешно устранена/существенно снижена создателем кода, или код-ревьюером.
Непреднамеренная сложность — это и есть цикломатическая сложность. Однако, эта метрика слишком тесно привязана к структуре кода, и хотя ЦС полезная метрика и широко применяется в разработке (и QA!), именно сложность кода, как таковую, она показывает не очень точно. Например, два сниппета ниже; как видим, подсчитана цикломатическая сложность каждого сниппета = 4, но код слева, сугубо визуально — он явно сложнее для восприятия, чем код справа.
 Цикломатическая сложность vs Когнитивная сложность
Цикломатическая сложность vs Когнитивная сложность
Поэтому в 2017 одной небольшой компанией была предложена концепция когнитивной сложности кода (то есть сложности восприятия человеком и как следствие сложности в обслуживании и тестировании), и, как заявляется, такой код будет гораздо лучше.
 Подсчет когнитивной сложности
Подсчет когнитивной сложности
Эта метрика основана на следующем:
- Игнорирование структур ЯП, «искусственно» сокращающих объем кода (особенно касается ЯП с часто обновляемым синтаксисом)
- Показатель когнитивной сложности увеличивается на 1 с каждым оператором, прерывающим поток выполнения (циклы, условия, тернарные операторы)
- Показатель увеличивается на 1 с каждой вложенной конструкцией (nested)
Если смотреть по показателю когнитивной сложности, то у Си-подобных языков получается средняя сложность кода около 25, в то время как все остальные ЯП — в среднем 15.
***
Заключение
Таким образом, мы рассмотрели общие сведения о таком показателе, как
сложность майнинга. В том числе изучили причины изменения данной величины.
Кроме того, определили принципы ее формирования. А также проследили динамику и
перспективы рассматриваемого коэффициента.
В настоящее время сложность майнинга находится на очень высокой своей отметке. Причем это можно утверждать в отношении любой криптовалюты, добываемой указанным методом. Однако, к добыче цифровых монет вычислениями интерес пользователей сохраняется. То есть те, кто только приходит к майнингу, может заработать на этом поприще. Однако и вложения здесь потребуются немалые. При этом риски сохраняются. Поэтому ступать ли на эту стезю, рисковать ли своими инвестициями и временем, решать каждому самостоятельно.
 Сложность майнинга – это очень важный показатель для формирования цены актива и вознаграждения “шахтерам”
Сложность майнинга – это очень важный показатель для формирования цены актива и вознаграждения “шахтерам”

























