Области применения числа N ≤ 100
Число N ≤ 100 используется в различных областях и сферах деятельности. В этом разделе рассмотрим некоторые области применения данного числа.
- Математика: В математике число N ≤ 100 может использоваться для описания множества натуральных чисел или как ограничение в задачах и уравнениях.
- Физика: В физике число N ≤ 100 может быть связано с измерениями, например, при описании физических величин или в пределах экспериментальных данных.
- Статистика: В статистике число N ≤ 100 может использоваться для анализа данных, включая категоризацию, сравнение или ранжирование.
- Программирование: В программировании число N ≤ 100 может быть использовано для ограничения циклов, массивов или других структур данных.
- Экономика: В экономике число N ≤ 100 может использоваться для описания стоимости, количества или других параметров товаров или услуг.
Это лишь некоторые области, в которых число N ≤ 100 может иметь значение и применение. В зависимости от контекста и конкретной задачи, значение данного числа может различаться и быть интерпретировано по-разному
Поэтому при работе с числом N ≤ 100 важно учитывать его конкретное значение и контекст использования
Что означает больше или меньше?
Зачем в математике используется выражение не менее?
Выражение «не менее» используется в математике для указания на минимальное значение и означает, что значение не может быть меньше указанного числа, но может быть больше.
В математике сравнение чисел по величине выражается с помощью знаков «больше» (>) и «меньше» (
Для обучения детей считают, что «больше» означает, что число находится на правой стороне при сравнении двух чисел, и «меньше» означает, что число находится на левой стороне. Как пример, можно использовать картинки с знаками «больше» и «меньше», чтобы дети могли смотреть на них и запоминать правило.
Другими способами для запоминания и понимания больше и меньше могут быть игры или задачи. Например, можно использовать задачу с голодным крокодилом, который «ест» числа и знаки. Дети могут смотреть на картинки или фигурки с числами и знаками, чтобы определить, что больше или меньше.
В общем, для понимания больше или меньше в математике необходимо знать, как писать знаки сравнения и как использовать их в неравенствах. Неравенство, где одна сторона больше числа на другой стороне, пишется с помощью знака «больше». Например, 5 > 3. Неравенство, где одна сторона меньше числа на другой стороне, пишется с помощью знака «меньше». Например, 3
Для упрощения запоминания можно использовать примеры с изображениями, таблицами или другими визуальными средствами. Это поможет детям лучше понять и запомнить правила сравнения чисел в математике.
Примеры использования «не больше» в программировании
Оператор «не больше» (<=) используется в программировании для сравнения двух переменных. Если первая переменная не больше или равна второй, то условие истинно и выполняется соответствующий код.
Пример:
int a = 5;
int b = 10;
if (a <= b) {
// Код, который выполнится, если a не больше или равна b
}
Этот код выполнится, так как переменная a не больше, чем b.
Также оператор «не больше» можно использовать в циклах. Например, цикл будет выполняться до тех пор, пока значение переменной не достигнет определенной границы:
for (int i = 0; i <= 10; i++) {
// Код, который будет выполняться в цикле
}
Этот цикл будет выполняться 11 раз, так как условие «i не больше 10» выполняется, пока значение i меньше или равно 10.
В ходе написания кода важно быть внимательным, используя оператор «не больше», чтобы избежать ошибок. Например, условие «a = a». Используя оператор «не больше», можно делать различные проверки в программировании, что упрощает работу с переменными и условиями в коде
Используя оператор «не больше», можно делать различные проверки в программировании, что упрощает работу с переменными и условиями в коде.
Сочетания клавиш для ввода знака «не более»
В математике знак «не более» обозначается символом «≤«. Для его ввода на клавиатуре можно использовать сочетание клавиш:
Операционная системаСочетание клавиш
| Windows | Удерживайте клавишу «Alt» нажатой и наберите на цифровой клавиатуре код символа «8804«. Затем отпустите клавишу «Alt». |
| Mac | Удерживайте клавишу «Option» нажатой и нажмите на клавиатуре символ «u». Затем наберите код символа «2264«. Затем отпустите клавишу «Option». |
| Linux | Удерживайте клавишу «Ctrl+Shift» нажатой и наберите на цифровой клавиатуре код символа «2264«. Затем отпустите клавиши «Ctrl+Shift». |
После ввода сочетания клавиш появится символ «≤» на экране, обозначающий знак «не более».
Решение неравенств: методы и приемы
Решение неравенств является важной частью математической теории и имеет широкий спектр использования в различных областях. Неравенства возникают, когда нужно сравнить два или более числа или выражения и найти диапазон значений, которые соответствуют условиям неравенства. Существуют различные методы и приемы для решения неравенств, которые зависят от типа и структуры неравенства
Рассмотрим некоторые из них:
Существуют различные методы и приемы для решения неравенств, которые зависят от типа и структуры неравенства. Рассмотрим некоторые из них:
- Графический метод. Для простых неравенств можно построить график функций, которые задают неравенство, и найти интервалы значений, удовлетворяющие условию.
- Алгебраический метод. Для многих неравенств можно применить алгебраические операции и свойства неравенств для поиска решений. Неравенство может быть упрощено путем сокращения или раскрытия скобок, применения операций сложения или вычитания к обеим сторонам неравенства.
- Метод декомпозиции. Некоторые сложные неравенства могут быть разложены на более простые неравенства с использованием свойств и регулярных выражений. Такой подход позволяет решить сложное неравенство путем последовательного решения простых частей.
- Метод проверки значений. Для некоторых неравенств можно использовать метод проверки значений, пробуя различные значения переменных и проверяя выполнение условия неравенства. Этот метод может быть полезен, когда другие методы не дают точного ответа.
- Метод замены переменных. Иногда замена переменных может привести к упрощению неравенства или позволить применить другие методы для его решения. Замена может быть произведена путем введения новой переменной или замены переменных на функции или выражения.
- Метод математической индукции. Для решения некоторых неравенств можно применить метод математической индукции, который основан на доказательстве условий неравенства для начального значения и доказательстве истинности для следующих значений.
Выбор метода или приема для решения неравенства зависит от его структуры и сложности
Важно также учитывать возможные ограничения на переменные и область значений, в которой ищутся решения
В заключение, решение неравенств включает в себя различные методы и приемы, которые позволяют определить диапазон значений, удовлетворяющих условиям неравенства. Выбор метода зависит от сложности и структуры неравенства, а также от специфики задачи.
Популярное

Навыки 15 декабря 2019

Математика 26 августа 2019 Найди закономерность Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.

Любовь к учебе 6 сентября 2019 Как решать ребусы? Разгадывание ребусов – отличное времяпровождение для любителей всевозможных головоломок и загадок. Это захватывающий процесс, суть которого заключается в том, чтобы расшифровать слово, фразу или предложение с помощью картинок и символов-подсказок: цифр, букв, запятых и прочих знаков.
Повторение изученной информации
Запись является неравенством тогда, когда содержит математические выражения, между которыми стоит знак «>» и «<». К примеру, 5 > 4 является неравенством, 2 < 7 также является неравенством. 2 + 3 < 7 также будет являться неравенством.
Неравенства, как и равенства, могут быть как неверными (например, 5 > 8 является неверным неравенством), так и верными (2 < 9 является верным неравенством).
Нестрогое неравенство может предполагать случай равенства правой и левой частей неравенства. Например, является верным неравенством.
Также, для того чтобы записать неравенство двух натуральных чисел, может использоваться знак . Знак M будет читаться как «не равно». К примеру, форма записи будет означать то, что a не равно b. Обычно, если нет оговорок, то понятие неравенства соотносится только с записями со знаками «>» и «<», «» и «».
Применение в правовых актах
Фраза «не превышает» является широко используемой в правовых актах и имеет важное значение при интерпретации и применении законодательства. Эта формулировка означает, что предельное значение или ограничение не может быть превышено. Если указано, что какое-то значение «не превышает» определенного уровня, это значит, что само значение может быть равным или меньше указанного уровня, но не больше
Если указано, что какое-то значение «не превышает» определенного уровня, это значит, что само значение может быть равным или меньше указанного уровня, но не больше
Эта формулировка означает, что предельное значение или ограничение не может быть превышено. Если указано, что какое-то значение «не превышает» определенного уровня, это значит, что само значение может быть равным или меньше указанного уровня, но не больше.
Применение этой формулировки в правовых актах имеет особое значение, когда необходимо установить ограничение или пороговое значение для определенного действия или явления.
Например, в законодательстве может быть указано, что максимальная скорость движения на дороге «не превышает» 60 километров в час. Это означает, что водители не могут превышать эту скорость и должны двигаться со скоростью в пределах 60 километров в час или ниже.
Также использование фразы «не превышает» может быть важным при установлении лимитов на размеры или количество разрешенных объектов или действий. Например, если указано, что максимальное количество пассажиров в транспортном средстве «не превышает» 4 человека, то это означает, что количество пассажиров может быть равным 4 или меньше, но не больше.
Таким образом, при интерпретации формулировки «не превышает» в правовых актах необходимо учитывать, что данное значение может быть равным или меньше указанного ограничения, но не может быть больше. Это позволяет установить ясные и однозначные правила и ограничения для обеспечения безопасности и соблюдения закона.
Не более это какой знак в математике
Содержимое
-
1 Не более это какой знак в математике
- 1.1 Знак «не более» в математике: смысл и обозначение
- 1.2 Видео по теме:
- 1.3 Правило использования знака «не более»
- 1.4 Примеры применения знака «не более»
-
1.5 Вопрос-ответ:
-
- 1.5.0.1 Как найти знак «не более» в математике?
- 1.5.0.2 Как использовать знак «не более» в уравнениях?
- 1.5.0.3 Как правильно интерпретировать знак «не более» в неравенствах?
- 1.5.0.4 Какие другие символы можно использовать для обозначения «не более» в математике?
- 1.5.0.5 Как решать неравенства с знаком «не более»?
-
- 1.6 Как найти знак «не более» на клавиатуре
- 1.7 Сочетания клавиш для ввода знака «не более»
- 1.8 Альтернативный способ ввода знака «не более»
- 1.9 Практическое использование знака «не более» в математике
- 1.10 Задачи с использованием знака «не более»
- 1.11 Решение задач с применением знака «не более»
В математике знак ‘не более’ представлен символом ≤ и означает, что одно число меньше или равно другому. Узнайте, как использовать этот знак и его значения в математических выражениях и уравнениях.
Математика — это наука, которая изучает свойства и отношения чисел, фигур и абстрактных объектов. В математике существует множество специальных символов и знаков, которые используются для обозначения различных математических операций и отношений. Один из таких знаков — это «не более».
Знак «не более» представляет собой комбинацию символов »
Пример: если «а» равно 5 и «b» равно 7, то можно записать «а ≤ b», где «≤» обозначает знак «не более». Это означает, что число «а» не превышает или равно числу «b».
В математике знак «не более» используется во множестве различных ситуаций. Например, его можно применять при сравнении чисел, определении диапазона значений или при проверке условий в математических уравнениях и неравенствах.
Знание знака «не более» и его применение в математике является важной частью учебного процесса. Оно помогает студентам и ученым лучше понимать и анализировать математические концепции и отношения между числами. Понимание правил и примеров использования этого знака является основой для успешного решения различных задач и уравнений в математике
Понимание правил и примеров использования этого знака является основой для успешного решения различных задач и уравнений в математике.
Что такое мета-тег Description и за что он отвечает
Description — это короткое описание страницы сайта, рассказывающее о том, чему она посвящена. Этот мета-тег располагается в блоке <head> </head> в коде страницы. Поисковые системы используют Description для отображения в сниппетах в поисковой выдаче.
Мы видим его каждый раз, когда что-то ищем в поисковиках.
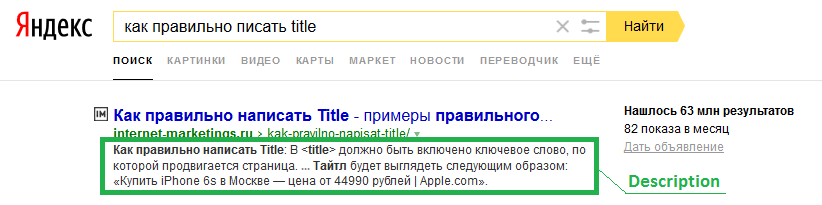
Грамотно заполненное описание более кликабельно (имеет высокий CTR) и положительно влияет на поведенческие факторы в выдаче.
Description можно задать в ручную, не заполнять или сгенерировать с помощью плагина. В том случае, если описание не задано, поисковик будет самостоятельно формировать его, отталкиваясь от содержания запроса.
Это интересно: Как составить семантическое ядро сайта
Что говорит история про знаки больше/меньше, равно?

Знаки больше/меньше, равно
Математические знаки являются компактной формой записи выражений, передающих различные соотношения между величинами. В первых математических трудах (Древний мир), согласно истории, все записывалось словесно. К примеру, знак «равно» был написан не в виде символа «=», а просто словами: 4 равно 4, хотя уже тогда стало понятно, что это совершенно неудобно, да и к тому же, у всех почерк разный, не всегда разобрать, что написано.
Древние цивилизации были довольно обособлены друг от друга, поэтому каждый народ изобретал свою систему записи математических выражений. До сих пор сохранились многие работы, которые дают современным людям знания о том, как в древности такие же люди, как и мы, сравнивали и анализировали мир при помощи своих самобытных обозначений. По мере роста населения, интеграции и смешивания народов, знаки становились все более и более похожими друг на друга, пока не появились общие обозначения, в том числе и для логических выражений больше, меньше и равно. Читайте далее.
Когда нужно менять знаки неравенства?
Может ли неравенство иметь знак равенства?
Символы неравенства — это символы, которые используются для обозначения отношений неравенства. … Хотя знак равенства технически не является неравенством символ, он обсуждается вместе с символами неравенства, поскольку он включен как часть нестрогих неравенств, таких как больше или равно (≥) и меньше или равно (≤).
Это между или между?
Между ними всегда должно быть два слова.. Хотя inbetween встречается часто, это опечатка, и ее нет ни в одном словаре английского языка. Ненужное добавление между ними также является распространенной грамматической ошибкой.
Что означает разница в математике?
Разница в том, результат вычитания одного числа из другого. … Итак, разница — это то, что остается от одного числа при вычитании из другого. В уравнении вычитания есть три части: уменьшаемое (число, из которого вычитается) вычитаемое (число, из которого вычитается)
В чем разница между этими двумя символами и ==?
Ответ: = символ часто используется в математических операциях. Он используется для присвоения значения заданной переменной. С другой стороны, символ ==, также известный как «равно» или «эквивалентно», представляет собой оператор отношения, который используется для сравнения двух значений.
Для чего нужен хаммерский сленг?
переходный глагол. Если вы говорите, что кто-то бьет другого человека, вы имеете в виду, что они атаковать, критиковатьили строго наказать другого человека. Демократы настаивали на том, что они будут продолжать бить президента по его налоговому плану.
Что означает этот символ ≅?
Символ ≅ официально определяется как U+2245 ≅ ПРИБЛИЗИТЕЛЬНО РАВНО. Это может означать: Приблизительное равенство. Конгруэнтность (геометрия)
Что такое V в математике?
Символы «V» в вопросе читателя — это ∨ и ∧, что означает «Логическое ИЛИ» и «Логическое И.» ∧ — заглавная греческая лямбда.
Не больше, чем то же самое, что и меньше?
Когда мы говорим «столько же, сколько» или «не более чем», мы имеем в виду «меньше или равно‘, что означает, что a может быть меньше b или равно b. Но когда мы говорим «по крайней мере», мы имеем в виду «больше или равно».
Добавляет больше, чем означает?
Сложение-сумма, всего, всего, всего, вместе, всего, общего числа, прибавления, прибавления, вырос по, более чем. Вычитание-минус, больше, отнять, меньше, меньше, вычесть, уменьшить на.
Какой знак наименьший?
Какой знак представляет хотя бы? Обозначение а ≥ b или а ⩾ b означает, что a больше или равно b (или, что то же самое, по крайней мере b или не меньше b).
Произведение означает умножение?
Продукт в математике число, которое получается путем умножения двух или более других чисел вместе. Например, если вы умножите 2 и 5 вместе, вы получите произведение 10. Умножение — важная часть математики.
Что значит найти разницу?
Нахождение разницы между двумя числами форма вычитания. В этих задачах по математике цель состоит в том, чтобы найти, сколько чисел лежит между двумя заданными числами. Это похоже на поиск диапазона между двумя числами.
В чем разница между 5 и 3?
если нам говорят найти разницу между 3 и 5, то мы обычно вычитаем 3 из 5,5-3=2 и, таким образом, мы говорим, что разница равна 2.
Можете ли вы закончить предложение с промежуточным звеном?
Окончание предложения предлогом не является ошибкой, но это немного менее формально. В электронных письмах, текстовых сообщениях и заметках для друзей все в порядке. Но если вы пишете исследовательскую работу или подаете деловое предложение и хотите, чтобы это звучало очень официально, избегайте заканчивать предложения предлогами.
Какое другое слово для между ними?
Промежуточные синонимы
На этой странице вы можете найти 6 синонимов, антонимов, идиоматических выражений и родственных слов для промежуточных значений, например: посредничать, середина, посередине, через, между и пространство между ними.
Как узнать, верно ли неравенство?
Если обе части неравенства умножаются или делятся на одно и то же положительное число, то полученное неравенство верно. Если обе части умножить или разделить на одно и то же отрицательное значение, направление неравенства изменится.
Что означает знак не равно?
Неравный, не равный. Некоторые сторонники превосходства белой расы приняли математический знак «≠(Not Equal or Not Equal To) как символ сторонников превосходства белой расы. Использование этого символа является попыткой заявить, что разные расы не равны друг другу (и подразумевать превосходство белой расы).
Оператор == (равенства)
Оператор (равенства) принимает операнды любого типа, если два операнда равны, возвращается значение , в противном случае — .
Если операнды имеют разные типы данных, PHP попытается преобразовать их перед сравнением к одному типу, например такое выражение вернёт значение , так как PHP автоматически приведет сравниваемые значения к одному типу данных. Аналогично, выражение вернёт значение , если переменная содержит значение 1. Если требуется избежать неявного преобразования типов при сравнении, то следует использовать оператор идентичности, который будет рассмотрен далее.
<?php $var1 = 5; $var2 = '5'; var_dump(14 == '14'); // вернет true var_dump(5 == 'hot'); // вернет false var_dump($var1 == $var2); // вернет true ?>
Определение термина: «Больше чем три»
Больше чем три — это выражение, которое указывает на количество, превышающее три. В своём прямом значении оно означает, что количество или значение являются больше, чем число три.
Часто выражение «больше чем три» используется для указания на некоторое множество или группу, которая содержит больше трех элементов или обладает свойствами, превышающими ограничения трех. Зачастую оно употребляется в говорах о количестве предметов, событий или действий, которые превышают указанное число три.
Выражение «больше чем три» также может использоваться в переносном смысле, обозначая что-то дополнительное, избыточное или преувеличенное. Например, «это утверждение содержит больше чем три аргумента» означает, что утверждение имеет несколько аргументов, возможно, больше, чем требуется для его поддержки.
Чтобы использовать выражение «больше чем три» в тексте, достаточно включить его в предложение, обозначающее число, множество или группу, которые превышают значение трех. Например: «В этом курсе представлено больше чем три направления изучения языка программирования», «На конференции было проведено больше чем три презентации».
Ключевая роль точного понимания фразы
Понимание фразы «не превышает» имеет ключевое значение при оценке размеров или значений. Формулировка «не превышает» означает, что полученное значение должно быть меньше либо равно указанной точки отсчета.
В контексте математики и статистики, использование фразы «не превышает» указывает на то, что рассматриваемое значение не может быть больше или выше данной точки. Например, если сказано, что количество объектов не превышает 5, это означает, что количество объектов может быть равным 5 или меньше.
Фраза «не превышает» часто используется в инструкциях и ограничениях. Она помогает установить пределы и границы, соблюдение которых является критически важным. Если фраза «не превышает» будет неправильно понята или неправильно интерпретирована, это может привести к ошибочным действиям или результатам, что может иметь нежелательные последствия.
Чтобы понять точное значение и интерпретацию выражения «не превышает», необходимо учитывать контекст, в котором используется данное выражение, и внимательно анализировать описание и указанные параметры
Также важно обратить внимание на любые ограничения или дополнительные пояснения, которые могут быть предоставлены
| Примеры | Интерпретация |
|---|---|
| Скорость не превышает 50 км/ч | Скорость может быть равной 50 км/ч или ниже этого значения. |
| Вес не превышает 100 кг | Вес может быть равным 100 кг или меньше. |
| Количество участников не превышает 20 | Количество участников может быть равным 20 или меньше. |
В заключение, правильное понимание и интерпретация выражения «не превышает» играет важную роль при работе с ограничениями и установкой точных параметров. Внимательное ознакомление с контекстом и дополнительной информацией поможет избежать ошибок и гарантировать правильное использование данного выражения.
Значок «примерно» («приблизительно»): как пишется, примеры

Значок «примерно»
Значок «примерно» пишется так: «≈». Похож на знак равно, но вместо прямых линий используются волнистые. Этот знак используется тогда, когда разницу между двумя числами можно не учитывать, потому что она слишком мала или незначительна.
Например:
На все человечество действует сила тяжести, именно из-за нее люди не улетают в открытый космос с Земли. При этом эта сила тяжести зависит от ускорения свободного падения, равного 9,8 метров в секунду в квадрате. Но в школе для упрощения расчетов и из-за незначительной разницы в результате вычислений ускорение свободного падения принимается за 10 метров в секунду в квадрате. То есть, можно сказать, что 9,8 метров в секунду ≈ 10 метрам в секунду.

П равно
Знак «примерно равно» используется, когда число округляется до определенного количества знаков. Например, со школьной скамьи всем известно число Пи — константа с бесконечным числом знаков после запятой. Обычно это число округляется до двух знаков после запятой. То есть можно записать, что Пи ≈ 3,14.
Что значит «меньше или равно»?
Разобрав, в какую именно сторону пишутся знаки больше, меньше или равно, разберём также ситуации, когда какое-либо значение меньше, но может быть также равно. Например, чайник может вмещать до 10 стаканов воды. Так сколько в нём может быть воды? Это может быть 10 стаканов или меньше 10 стаканов. Пока мы не измерим количество жидкости, то всё, что мы можем сказать о наполнении стакана, то это то, что оно «меньше или равно» 10 стаканам.
Для показа данного отношения с помощью символов мы добавляем внизу дополнительную строку символа больше или меньше. Например:
- Знак «больше или равно»: ≥
- Знак «меньше или равно»: ≤
Зачем использовать данные знаки? Дело в том, что есть вещи, полной информации о которых мы не имеем, но, тем не менее, можем о них что-то полагать. Таким образом, у нас есть различные способы сказать то, что мы знаем, хоть и не до конца (это может быть полезно).
Пример:
У Олега было 10 яблок, но он потерял несколько. Сколько у него сейчас?
Ответ: У него должно быть меньше 10 яблок.
То есть: яблоки у Олега < 10
Если у Олега все еще есть яблоки, мы также можем сказать, что у него больше нуля яблок? Конечно.
То есть: яблоки у Олега > 0
Но если бы мы думали, что Олег мог потерять все свои яблоки, мы бы сказали:
яблоки у Олега ≥ 0
Другими словами, количество яблок больше или равно нулю.
Математическое определение «не менее»
Например, если у нас есть задача о сравнении количества кубиков на двух досках, то мы можем сказать, что на одной доске количество кубиков не менее 51. Это можно записать следующим образом: 51 ≥ (количество кубиков на другой доске).
В неравенствах с использованием знаков «» мы указываем, что одно число меньше или больше другого. Однако в математике такие знаки не подразумевают «или равно». Поэтому, чтобы точно выразить понятие «не менее», мы используем знак «≥».
Какие другие выражения можно использовать вместо «не менее»?
Вместо выражения «не менее» можно использовать следующие выражения: «не ниже», «не менее чем», «как минимум», «по меньшей мере». Все эти выражения имеют одно значение — указывают на минимальное значение, которое может быть равным данному.
Эти арифметические знаки очень важны для быстрого и правильного решения задач в математике. Иногда их можно запомнить в виде игры: знак «≥» выглядит как крокодил, у которого больше зубов внизу, а знак «≤» выглядит как крокодил, у которого меньше зубов внизу.
Есть несколько способов сравнения чисел и записи неравенств с использованием знака «≥». Например:
- 5 ≥ 3 — число 5 не менее числа 3;
- 9 ≥ 9 — число 9 не менее числа 9;
- −2 ≥ −5 — число −2 не менее числа −5.
Для быстрого решения задачи можно использовать следующие сведения:
- При сложении или умножении на одно и то же положительное число, неравенство сохраняет свое направление. Например, если у нас есть неравенства 3 ≥ 2 и 5 ≥ 4, то при сложении их получится 8 ≥ 6, что также является верным.
- В неравенствах с отрицательными числами знак неравенства меняется при умножении на отрицательное число. Например, если у нас есть неравенство 4 ≥ 3, то при умножении его на −1 получится −4 ≤ −3.
- Общие правила сравнения чисел также применимы в неравенствах с использованием знака «≥». Например, двойное неравенство «3 > 2 > 1» можно записать как «3 ≥ 2 ≥ 1».
Знание математических знаков и правил сравнения чисел помогает детям, начиная с дошкольного возраста, решать задачи быстрее и легче. С их помощью можно сравнивать количество предметов, решать задачи о количестве еды и питья, а также использовать их для игры в «голодного крокодила» или «задачу с клавиатурой».
Таким образом, понимание понятия «не менее» и правила использования знака «≥» в математических неравенствах является важным для развития математических навыков.
Как пишется знак больше меньше в математике
Знаки «больше (>)» или «меньше (<)» обычно используются для отображения отношений между числами. Они позволяют продемонстрировать, какое число имеет большее или меньшее значение, и применяются с целью помочь учащимся разобраться с соотношениями чисел. Знаки «больше» или «меньше» также часто известны как знаки «больше чем» и «меньше чем».
Широкий конец данного знака всегда обращён к большему числу. Например:
25 > 10
100 > 50
500 > 200
Знак «больше» (>) означает, что число перед знаком «больше» всегда больше числа, которое находится после данного знака.
200 > 100
Знак меньше (<) означает, что число перед данным знаком всегда меньше, нежели число после данного знака. Как видим, визуально знак «больше» и «меньше» — это просто перевернутые версии одного и того же символа.
100 < 200
Знак равенства (=) означает, что число после знака равно числу перед знаком.
Важно! Знак равенства не является показателем результата работы над числами (например, 3+5=8). Данный знак показывает, что сумма чисел слева равна сумме чисел справа
То есть 3+5 слева равно числу справа, которым и является 8.
Когда же два значения определенно не равны, тогда мы используем пример со знаком «не равно»: 2+2 ≠ 9. То есть сумма значений чисел слева (4) не равно значению чисел справа (9).
Не больше как пишется в математике
Содержимое
1 Не больше как пишется в математике
1.1 Определение понятия «не больше»
1.2 Видео по теме:
1.3 Отличие «не больше» от «меньше или равно»
1.4 Примеры использования «не больше» в решении задач
1.5 Вопрос-ответ:
1.5.0.1 Что такое «не больше» в математике?
1.5.0.2 Можно ли использовать «не больше» вместо «меньше или равно»?
1.5.0.3 Как правильно записывать «не больше» в математических формулах?
1.5.0.4 Какую роль играют знаки «≤» и «≥» в математике?
1.5.0.5 Какие другие математические операции могут использоваться вместе с «не больше»?
1.5.0.6 Как понять, что число не больше другого числа?
1.5.0.7 Можно ли записать «не больше» как «меньше» в математической формуле?
1.6 Как правильно записывать «не больше» в математической нотации
1.7 Как прочитать «не больше» на английском языке
1.8 Стандартные обозначения «не больше» в различных областях математики
1.9 Схематическое изображение «не больше» в графике
1.10 Примеры использования «не больше» в программировании
1.11 Ошибки, допускаемые при использовании «не больше»
1.12 Как правильно перевести «не больше» на другие языки
1.13 Важность правильного использования «не больше» в математических выражениях
Правильное написание математических знаков и символов: не больше. Примеры использования и объяснение правил написания в математике.
В математике существует множество математических знаков и символов, которые используются для обозначения различных функций, операций и переменных. Один из таких знаков — символ «≤» (меньше или равно), который часто используется в неравенствах и уравнениях. Однако, на практике возникает ряд вопросов относительно того, как правильно записывать этот символ.
В данной статье мы рассмотрим различные способы записи символа «≤», а также ответим на наиболее часто задаваемые вопросы по этой теме. Вы узнаете, как правильно записывать этот символ в ручную и в различных программных приложениях, а также узнаете о возможных затруднениях, связанных с его использованием.
Также вы узнаете, как символ «≤» связан с другими математическими знаками, такими как «>», »
Примеры использования «не больше» в решении задач
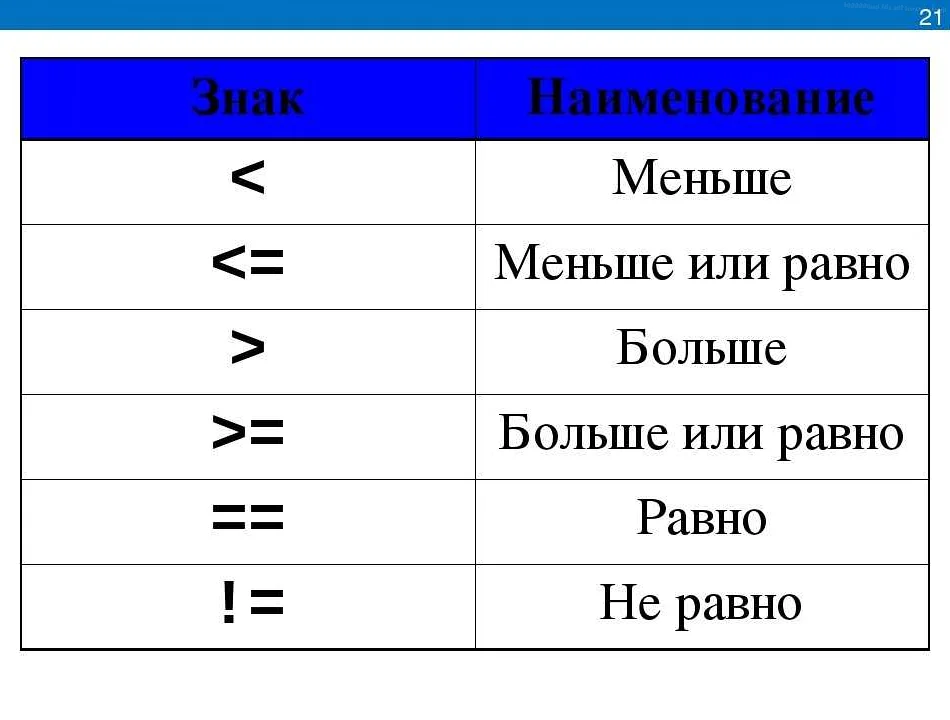
В математике «не больше» обозначается символом ≤. Он означает, что значение слева от знака не превышает значение справа от знака. Например, выражение 2 ≤ 5 означает, что 2 не больше 5.
Для решения задач, где используется «не больше», важно понимать, как использовать этот математический знак. Рассмотрим пример:
В классе учится 25 учеников
Группу выходного дня составляют не больше 12 человек. Сколько учеников может составить группу выходного дня?
В классе учится 25 учеников. Группу выходного дня составляют не больше 12 человек. Сколько учеников может составить группу выходного дня?
- Задачу можно решить, используя формулу: 25 — x ≤ 12, где x — количество учеников в группе выходного дня.
- Выразим x: x ≤ 25 — 12, x ≤ 13.
- Ответ: группу выходного дня может составить не более 13 учеников.
В других задачах «не больше» может использоваться для сравнения различных величин. Например:
Мария купила 5 кг яблок и 3 кг груш. Общий вес фруктов не больше 10 кг. Можно ли сказать, что максимальный вес фруктов, которые купила Мария, не превышает 9 кг?
- Максимальный вес фруктов равен 5 + 3 = 8 кг.
- 8 кг не больше 10 кг, значит, можно сказать, что Мария купила фрукты общим весом, не превышающим 10 кг.
- Ответ: да, можно сказать, что максимальный вес фруктов, купленный Марией, не превышает 9 кг, так как 8 кг не больше 9 кг.
Как ставить знаки сравнений на компьютере?

Знаки сравнений на компьютере
Знак «равно» на клавиатуре компьютера находится над всеми буквами в конце ряда чисел на клавише вместе со знаком «плюс». Чтобы напечатать «=», нужно просто нажать на эту кнопку. Вот еще как можно ставить знаки сравнений:
- Знаки «больше» и «меньше» располагаются на клавишах с буквами Ю и Б соответственно. Чтобы напечатать их, нужно переключиться на английский язык, зажать клавишу Shift и нажать на нужную букву.
- Знаки «намного меньше» и «намного больше» печатаются посредством двойного нажатия на соответствующую букву.
- Для знаков «больше или равно» и «меньше или равно» нет специальных кнопок. Но можно просто сначала написать знак больше или меньше, а затем приписать знак равенства. И получится либо >=, либо <=.
Технологию написания знака неравно берут из языков программирования. Поэтому можно написать <>, != или просто написать словами «не равно». В текстовых редакторах и других программах обычно есть встроенный инструментарий, который позволяет писать эти знаки, как хочется, в том числе в стандартном виде. Поэтому можно выбирать любой вариант.
Итак, знаки сравнения широко используются при записи математических выражений. Они очень удобны, компактны, и их использование понятно на бытовом уровне даже ребенку
Нетяжело научиться оперировать ими и находить верное решение, если следовать ценным советам при работе с ними. Каждому человеку важно познакомиться с символами больше, меньше и равно и немножко приблизиться к неизведанной науке математике
Оператор > (больше)
При использовании оператора (больше) сравнение возвращает только в том случае, если значение слева от оператора больше значения справа от него. Как и другие операторы, оператор работает не только с числовыми значениями, но и со строковыми. Но как одна строка может быть больше другой?
При работе со строками буква в нижнем регистре больше буквы в верхнем регистре. При сравнении строк PHP сначала проверяет на несовпадение первую букву строки. Если разницы не обнаруживается, происходит переход к следующему символу и т.д., пока не будет найдено различие или не будет достигнут конец строки. Если два значения с каждой из сторон оператора будут равны, оператор также вернет .
<?php
var_dump(4 > 3); // вернет true
var_dump('Hi' > 'hi'); // вернет false
var_dump(1 > 1); // вернет false
?>


























