Округление ⭐ чисел: виды, особенности математического до целого числа, примеры с ответами

Как вычислить количество значащих цифр в числе?

Значащие цифры — это цифры, которые влияют на значение числа и не являются нулями в его начале или конце.

Количество значащих цифр в числе можно вычислить по следующим правилам:

Все ненулевые цифры в числе являются значащими.
Нули между ненулевыми цифрами в числе также считаются значащими.
Нули, стоящие перед первой ненулевой цифрой, не являются значащими.
Нули, стоящие после последней ненулевой цифры, также не являются значащими.
Нули, находящиеся в конце дробной части числа, не считаются значащими.

Примеры:

ЧислоКоличество значащих цифр

123	3
0.00340	3
2000	1
0.00050	1

Знание количества значащих цифр в числе может быть полезно при округлении чисел или при работе с точными значениями в научных вычислениях.

Что такое значащие цифры?

Значащие цифры — это цифры в числе, которые имеют значение и влияют на точность измерения. Они являются наиболее точными цифрами в числе и используются для определения количества десятичных знаков в измерении.

Например, в числе 12.345 эти цифры все являются значащими, так как каждая цифра имеет свое значение. Однако, в числе 12.00 только две первые цифры считаются значащими, а две последние нули не имеют значения, так как они не влияют на точность измерения.

Значащие цифры используются для указания точности измерения и для сокращения размера числа, сохраняя тем самым его значимость

Это особенно важно при работе с научными данными и экспериментами, где точность измерений достигает высоких уровней

Использование функций округления

Иногда нужно поменять точность расчетов с числовыми данными не для всего файла, а лишь для определенной области ячеек. В этом случае лучшим решением будет использование встроенных функций для работы с округлением чисел, которых существует несколько видов. Вот самые удобные и наиболее популярные:

ОКРУГЛ – округление до числа с указанным количеством знаков после запятой по правилам математики.
ОКРУГЛВВЕРХ – округление до ближайшего большего значения (по модулю).
ОКРУГЛВНИЗ – округление до ближайшего меньшего значения (по модулю).
ОКРУГЛТ – округление числа с желаемой точностью.
ОКРВВЕРХ – округление с избытком до ближайшего числа, которое кратно заданному значению точности.
ОКРВНИЗ – округление с недостатком до числа ближайшего числа, которое кратно заданному значению точности.
ОТБР – округление до целого числа путем отбрасывания цифр после запятой.
ЧЁТН – округление до ближайшего четного числа.
НЕЧЁТ – округление до ближайшего нечетного числа.

Обобщенная формула для первых трех функций выглядит так: ФУНКЦИЯ(;). Например, для округления числа 3,14159265 до двух знаков после запятой, нам понадобится следующая формула: =ОКРУГЛ(3,14159265;2).

Пишем ее в нужную ячейку, не забывая в начале поставить знак равно.

После набора формулы щелкаем клавишу Enter и получаем в результате число 3,14.

В формулах функций ОКРУГЛТ, ОКРВВЕРХ и ОКРВНИЗ в качестве второго аргумента указывается кратность округления. Например, если стоит задача округлить число 13 до ближайшего числа, делящегося на 5 без остатка, следует написать следующую формулу: =ОКРУГЛТ(13;5).

Результатом вычисления будет число 15.

Последние три функции (ОТБР, ЧЁТН и НЕЧЁТ) используют всего 1 аргумент – само число или ячейка. Первая из них просто вернет его целую часть, а вторая и третья – ближайшее четное или нечетное числа, соответственно.

Сами функции можно прописать как внутри ячейки, так и в верхней строке формул, которая находится справа от надписи fx.

После того, как вы начнете вводить название функции, программа выдаст подсказки, благодаря которым можно выбрать точное название и избежать возможных опечаток. Перед написанием формулы не забывайте ставить знак равно (“=”).

В дополнение ко всему, есть возможность вызвать функци через вкладку “Формулы”. Откройте ее и выберите “Математические”. Появится список всех функций, расположенных по алфавиту, поэтому для поиска округления (ОКРУГЛ) нужно идти в нижнюю часть списка.

После того, как мы выберем нужную функцию, откроется окно для ее настройки.

В строке “Число” пишем координаты ячейки, значение которой нужно округлить. Также, вместо того, чтобы писать адрес ячейки вручную, можно просто находясь курсором в строке “Число” щелкнуть левой кнопкой мыши по нужной ячейке.

Далее переходим к строке “Число разрядов” и здесь пишем число знаков после запятой. Допустим, в нашем случае, пусть это будет 2.

После того, как все заполнено, нажимаем “OK” и получаем результат в первой строке, куда была вставлена функция округления.

Чтобы применить расчеты к остальным строкам столбца, наводим мышью на нижний правый угол ячейки, содержащей формулу. Курсор поменяет свой вид на небольшой крестик. Теперь, зажав его левой кнопкой мыши тянем формулу на оставшиеся строки, по которым нужно произвести расчет, после чего отпускаем кнопку.

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Округление ⭐ чисел: виды, особенности математического до целого числа, примеры с ответами

Округление в python — round, int, модуль math

Правила (алгоритм) округления чисел. примеры. видео

Как округлить число в экселе 2007, 2010, 2013 и 2016

Калькулятор округления значащих цифр — calculator.io

Как округлить число в excel в большую и меньшую сторону | ichip.ru

Округление чисел в python – round, int, функции модуля math

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Округление десятичных дробей

При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:

Разряды целой части:

разряд единиц;
разряд десятков;
разряд сотен;
разряд тысяч.

Разряды дробной части:

разряд десятых;
разряд сотых;
разряд тысячных

Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды

Очень важно не путать их:

Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.

Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых

Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной

Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):

123,456 ≈ 120

Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:

Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:

123,456 ≈ 123,0

Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:

123,456 ≈ 123,0 ≈ 123

Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:

Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,500

Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:

Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями

123,456 ≈ 123,460

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Алгоритм округления чисел

Процесс округления числа в основном означает нахождение числа с меньшим количеством цифр, значение которого близко к значению исходного числа. Например, интуитивно понятно, что 6,1 округлится до 6, поскольку оно «ближе» к 6, чем к 7. Аналогично, 6,2 , 6,3 и 6,4 округлятся до 6. Тогда как 6,9 округлится до 7, так как он ближе к 7, чем к 6. То же самое с 6,8 , 6,7 и 6,6. Но что делать с 6,5? Он находится ровно посередине между 6 и 7. Существует несколько различных правил округления, здесь мы рассмотрим наиболее распространенный метод. В наиболее распространенном методе округления 5 округляется «вверх», так что 6,5 округляется до 7. Алгоритм округления чисел в этом случае состоит из следующих шагов:

Определите количество значащих цифр, которое вы хотите сохранить.
Посмотрите на последнюю цифру, которую вы сохраняете. Если следующая цифра меньше 5, оставьте последнюю цифру прежней; если следующая цифра больше или равна 5, увеличьте последнюю значащую цифру на 1.

Например, давайте округлим каждое число до двух значащих цифр: 1015, 876. Начнем с 1015:

Мы хотим округлить до 2 значащих цифр, поэтому последняя цифра, которую мы сохраняем (и не обращаем в 0) — это ноль: 1015 — здесь мы сохраняем жирные цифры, а остальные обращаем в ноль.
Посмотрим на цифру, следующую за нулем — это единица. 1 меньше 5, поэтому последнюю значащую цифру оставляем прежней. Число становится равным \$1\bar{0}00\$. Горизонтальная линия над второй цифрой показывает, что это число округляется до второй значащей цифры.

Теперь давайте посмотрим на 876:

Последняя цифра, которую мы сохраняем — 7, вторая цифра числа: 876 — опять же, мы сохраняем жирные цифры, а остальные превращаем в нули.
Следующая цифра после 7 — 6. 6 больше 5, поэтому к последней сохраненной цифре нужно прибавить 1: 7 + 1 = 8. Итоговое число будет \$8\bar{8}0\$. Здесь также над второй цифрой добавлена горизонтальная черта, чтобы показать, что число было округлено до второй значащей цифры.

Округление десятичных дробей

Алгоритм округления десятичных дробей такой же, как и алгоритм округления целых чисел

Важно отметить, что ведущие нули не являются значащими цифрами, поэтому они не учитываются при выборе последней сохранившейся цифры. Например, давайте округлим каждое число до трех значащих цифр: 9.05675, 0.01234. Начиная с 9,05675, получаем:

Начиная с 9,05675, получаем:

Мы хотим округлить до трех значащих цифр, поэтому последняя сохраняемая цифра — 5: 9,05675, где мы сохраняем только жирные цифры.
Смотрим на цифру после 5 и видим, что это 6. 6 больше 5, поэтому последнюю значащую цифру нужно увеличить на 1: 5 + 1 = 6. Итоговое число равно 9,06000. В отличие от целых чисел, нули в конце числа не меняют значение окончательного ответа, поэтому их можно удалить. Окончательный ответ — 9,06.

Теперь рассмотрим 0,01234:

Мы хотим округлить до 3 значащих цифр, поэтому последняя цифра, которую мы оставляем, — 3

Обратите внимание, что первые нули не считаются значащими цифрами: 0,01234, где мы сохраняем только жирные цифры.
Цифра после 3 — 4. 4 меньше 5, поэтому последняя цифра не меняется, и окончательное число равно 0,01230, или 0,0123.

Правила округления чисел

Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:

Если цифра равняется или больше 5, то значащее значение округляют с увеличением на 1.
Если цифра меньше 5, то значение округляют без увеличения.

Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.

Функции округления в excel - statanaliz.info

Округление чисел 5 класс онлайн-подготовка на ростелеком лицей | тренажеры и разбор заданий

Приближенные значения чисел. округление чисел

В математике округление числа до двух значащих цифр означает, что все цифры после второй значащей цифры будут отброшены, а вторая значащая цифра будет

Округление чисел в excel: 4 рабочих способа

Как округлять числа правильно? | калькулятор округления чисел

Округление чисел после запятой – правила

Приближенные значения чисел. округление чисел / десятичные дроби / справочник по математике 5-9 класс

Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.

Что мы узнали?

Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.

/5

Вопрос 1 из 5

Алгоритм округления чисел

Определите количество значащих цифр, которое вы хотите сохранить.
Посмотрите на последнюю цифру, которую вы сохраняете. Если следующая цифра меньше 5, оставьте последнюю цифру прежней; если следующая цифра больше или равна 5, увеличьте последнюю значащую цифру на 1.

Например, давайте округлим каждое число до двух значащих цифр: 1015, 876. Начнем с 1015:

Мы хотим округлить до 2 значащих цифр, поэтому последняя цифра, которую мы сохраняем (и не обращаем в 0) — это ноль: 1015 — здесь мы сохраняем жирные цифры, а остальные обращаем в ноль.
Посмотрим на цифру, следующую за нулем — это единица. 1 меньше 5, поэтому последнюю значащую цифру оставляем прежней. Число становится равным \$1\bar{0}00\$. Горизонтальная линия над второй цифрой показывает, что это число округляется до второй значащей цифры.

Теперь давайте посмотрим на 876:

Последняя цифра, которую мы сохраняем — 7, вторая цифра числа: 876 — опять же, мы сохраняем жирные цифры, а остальные превращаем в нули.
Следующая цифра после 7 — 6. 6 больше 5, поэтому к последней сохраненной цифре нужно прибавить 1: 7 + 1 = 8. Итоговое число будет \$8\bar{8}0\$. Здесь также над второй цифрой добавлена горизонтальная черта, чтобы показать, что число было округлено до второй значащей цифры.

Округление десятичных дробей

Алгоритм округления десятичных дробей такой же, как и алгоритм округления целых чисел

Начиная с 9,05675, получаем:

Мы хотим округлить до трех значащих цифр, поэтому последняя сохраняемая цифра — 5: 9,05675, где мы сохраняем только жирные цифры.
Смотрим на цифру после 5 и видим, что это 6. 6 больше 5, поэтому последнюю значащую цифру нужно увеличить на 1: 5 + 1 = 6. Итоговое число равно 9,06000. В отличие от целых чисел, нули в конце числа не меняют значение окончательного ответа, поэтому их можно удалить. Окончательный ответ — 9,06.

Теперь рассмотрим 0,01234:

Мы хотим округлить до 3 значащих цифр, поэтому последняя цифра, которую мы оставляем, — 3

Округление десятичных дробей

Округление десятичных дробей требует учёта количества знаков после запятой. Это может быть полезно для упрощения расчётов или для представления данных в удобном формате.

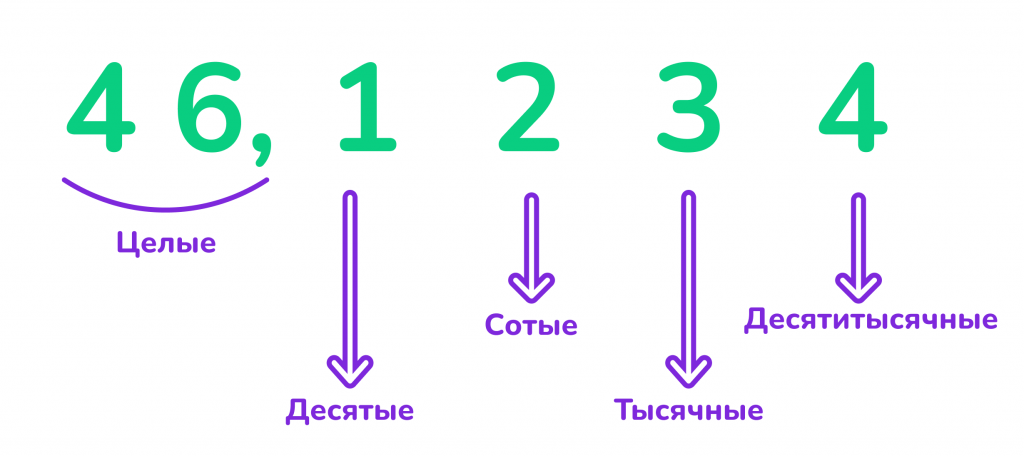
Алгоритм округления десятичных дробей

1. Определение разряда округления:

Определите, до какого разряда нужно округлить число (до десятых, сотых, тысячных и т. д.).

2. Проверка следующей цифры:

Посмотрите на цифру, которая находится сразу после разряда округления.

3. Применение правила округления:

Если цифра после разряда округления меньше 5, цифра в округляемом разряде остаётся без изменений.

Если цифра после разряда округления равна 5 или больше, цифра в округляемом разряде увеличивается на 1.

4. Отбрасывание лишних цифр:

Все цифры, находящиеся справа от округляемого разряда, отбрасываются.

Примеры округления десятичных дробей

Пример 1. Округление до ближайшей десятой доли.

Число: 4,73

Округляем до десятых.
Следующая цифра: 3 (меньше 5).
Округлённое число: 4,7.

Пример 2. Округление чисел до ближайшей сотой доли

Число: 9,856

Округляем до сотых.
Следующая цифра: 6 (больше 5).
Округлённое число: 9,86.

Пример 3. Округление чисел до ближайшей тысячной доли

Число: 3,14159

Округляем до тысячных.
Следующая цифра: 5 (равна 5).
Округлённое число: 3,142.

Зачем нужны значащие цифры?

Значащие цифры являются важным инструментом в математике и науке. Они позволяют выразить точность измерений и оценок с помощью чисел. Кроме того, значащие цифры используются для представления результатов вычислений и математических моделей.

Кроме того, значащие цифры используются для оценки результатов многих научных и инженерных расчетов. Например, если мы вычисляем силу тяжести на земле, мы будем использовать точное значение для ускорения свободного падения на поверхности Земли, а оставшиеся цифры будут написаны в соответствии с точностью измерения.

Выводя итоги, можно сказать, что значащие цифры играют важную роль в науке и энжиниринге. Они помогают представлять точность измерений и оценок с помощью чисел, а также выражать результаты вычислений и математических моделей.

Шаг 3: Округление числа до 2 значащих цифр

После того как мы нашли две первых значащих цифры числа, необходимо провести округление.

Для округления числа до двух значащих цифр, нужно проанализировать третью значащую цифру. Если она меньше 5, то вторая значащая цифра остается без изменений и все остальные цифры обнуляются. Если третья значащая цифра больше или равна 5, то вторая значащая цифра увеличивается на 1, а все остальные цифры обнуляются.

Вот пример:

Дано число: 3.149

Первые две значащие цифры: 3.1

Третья значащая цифра: 4 (меньше 5)

Округленное число: 3.1

Дано число: 3.159

Первые две значащие цифры: 3.1

Третья значащая цифра: 9 (больше или равна 5)

Округленное число: 3.2

Таким образом, округление числа до двух значащих цифр позволяет получить более удобное представление числа, при котором сохраняется необходимая точность, но избавляемся от незначащих цифр.