Содержание
-
Слайд 1
Путешествие в страну Симметрию
Урок — исследование
УМК «Гармония»
Окружающий мир
2 классУчитель:Гришина Марина Викторовна
2016 год -
Слайд 2
«Поиск информации»
телевидение
энциклопедии
справочники
интернет
Научно-исследовательская
лаборатория -
Слайд 3
Исследование- научный труд.
Исследовать- подвергать научному исследованию.
Исследователь- человек, который занимается научным исследованием.
Толковый словарь
«Давай обсудим» -
Слайд 4
-
Слайд 5
ММЕ
3
Я
симметрия -
Слайд 6
Какова же цель нашего исследования?
Цель нашего исследования:СОБРАТЬ ФАКТЫ О СИММЕТРИИ
-
Слайд 7
«Как узнать новое?»
-
Слайд 8
«Симметрия»-
слово греческое ( συμμετρία), оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”, неизменность при каких-либо преобразованиях.«Знаешь ты – знаю и я»
-
Слайд 9
Вопрос исследования:
на какие группы
(виды) можно
распределить симмет-
ричные предметы? -
Слайд 10
Цель исследования:
изучить материалы о каждом
виде симметрии -
Слайд 11
Правила работы в группах
Умей не только слушать, но и слышать.
Умей не только смотреть, но и видеть.
Умей не только думать, но и вдуматься.
-
Слайд 12
Работа в группах
Группа 1
Группа 2
Группа 3Внимательно прочитайте текст. Подчеркните интересные факты о данном виде симметрии.
Прочитайте задания на рабочем листе и выполните их.
Подготовьтесь к выступлению, пользуясь «Помощником ответа». -
Слайд 13
Фигуры, симметричные относительно оси
Главное отличие – одинаковость частей.Ось симметрии – линия, делящая изображение на одинаковые половинки.
Осевая симметрияГруппа 1
-
Слайд 14
Центрально – симметричныефигуры
Поворотная симметрия
Главное отличие – повторяемость при повороте.
Главный закон – здесь что ни повернётся, таким же остаётся.Группа 2
-
Слайд 15
-
Слайд 16
Облака- белокрылые лошадки.
Облака, что вы мчитесь без оглядки.
Не смотрите вы, пожалуйста, свысока..
А по небу прокатите нас, облака. -
Слайд 17
Мимо белого яблока луны,
Мимо красного яблока заката.Облака из неведомой страны,
К нам спешат и опять бегут куда-то. -
Слайд 18
-
Слайд 19
Главное отличие – повтор фигур на одинаковом расстоянии друг от друга.
Группа 3
Переносная симметрия
-
Слайд 20
Национальные узоры, орнаменты
Группа 3
С помощью симметрии выполняются национальные узоры, орнаменты.
Переносная симметрия
-
Слайд 21
Выводы и результаты
исследованияСимметрия многообразна и многолика.
Симметричныеобъекты окружают нас со всех сторон.
Симметричночеловеческое тело.
Симметричны животные, рыбы, насекомые.
Симметриявстречается часто и повсеместно – как в природе, так и в человеческом творчестве.
Симметрияприсутствует в регулярности смены дня и ночи; времён года.«Мы узнали, что…»
-
Слайд 22
переносная
поворотная
осевая -
Слайд 23
В природе
-
Слайд 24
В изделиях человека
-
Слайд 25
-
Слайд 26
текст на с.104 – 106;
закончить рисунок в РТ;
разгадать крестословицу.
Домашнее задание -
Слайд 27
На уроке мне было всё понятно!
У меня возникли некоторые вопросы.
Я многое не понял.
Рефлексия -
Слайд 28
МОЛОДЦЫ!
-
Слайд 29
Одна ось симметрии
Две оси симметрии
А
И
З
Ж
Е
Д
Г
В
Б
О
Н
Л
К
М
П
Р
С
У
Ф
Х
Э
Ю
Т
Имеют ли буквы русского алфавита ось симметрии? -
Слайд 30
О.Т. Поглазова, В.Д. Шилин Окружающий мир, 2 класс- Смоленск «Ассоциация XXІ век», 2015
О.Т.Поглазова Окружающий мир, 2 класс. Рабочая тетрадь — Смоленск «Ассоциация XXІ век», 2015
Толковый словарь В.И.Даля
Я иду на урок в начальную школу: Книга для учителя.- М.: Издательство «Первое сентября»
Узоры, орнаменты — vishivka-felizy.blogspot.com
Смайлики — fotki.yandex.ruРаботу выполнила
учитель начальных классов
Гришина Марина ВикторовнаПрезентация опубликована на сайте — viki.rdf.ru
Ресурсы
Посмотреть все слайды
Как проверить правильность ответов в рабочей тетради по симметрии
При проверке рабочей тетради по симметрии второго класса нужно обратить внимание на несколько ключевых моментов. Во-первых, следует проверить, что ученик правильно определил, какие фигуры являются симметричными, а какие не являются. Для этого нужно сравнить ответы ученика с правильными определениями симметрии, представленными в учебнике или пособии
Для этого нужно сравнить ответы ученика с правильными определениями симметрии, представленными в учебнике или пособии
Во-первых, следует проверить, что ученик правильно определил, какие фигуры являются симметричными, а какие не являются. Для этого нужно сравнить ответы ученика с правильными определениями симметрии, представленными в учебнике или пособии.
Во-вторых, нужно убедиться, что ученик правильно нашел все осевые симметрии в заданных фигурах. Осевая симметрия означает, что фигуру можно разделить на две равные части с помощью прямой линии или оси симметрии. Ученик должен указать все осевые симметрии, а также правильно обозначить их на рисунке.
Также следует проверить, что ученик правильно отразил фигуры относительно заданной оси симметрии. Ученик должен сделать зеркальное отражение фигуры, сохраняя ее размеры и форму
Важно проверить, что отраженная фигура соответствует оригинальной и является симметричной по отношению к заданной оси
При проверке ответов ученика также важно обратить внимание на аккуратность выполнения работы, правильное использование инструментов (линейки, цветных карандашей и т.д.), а также на наличие всех необходимых подписей и пометок на рисунках. В итоге, правильность ответов в рабочей тетради по симметрии можно оценить, сравнивая их с правильными определениями и образцами, а также учитывая выполнение всех требований и условий задания
В итоге, правильность ответов в рабочей тетради по симметрии можно оценить, сравнивая их с правильными определениями и образцами, а также учитывая выполнение всех требований и условий задания
В итоге, правильность ответов в рабочей тетради по симметрии можно оценить, сравнивая их с правильными определениями и образцами, а также учитывая выполнение всех требований и условий задания.
Проверка рабочей тетради по симметрии поможет ученикам закрепить и углубить свои знания о симметричных фигурах, а также научиться применять их в практических задачах.
Общие сведения
Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.
Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.
Любого вида многоугольник состоит из следующих частей:
Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.
Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.
Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.
https://youtube.com/watch?v=FZQXnOdUeeI
Основные принципы симметрии и их применение в математике
Симметрия — это особое свойство фигур, которое характеризуется их равенством относительно определенной оси, линии, или плоскости. В математике симметрия играет важную роль и применяется в различных областях, таких как геометрия, алгебра, теория чисел и другие.
Основные принципы симметрии, которые применяются в математике, включают:
- Осевую симметрию. В случае осевой симметрии фигура имеет ось симметрии, вдоль которой она делится на две одинаковые части. Осевая симметрия широко применяется в геометрии, например, при рисовании фигур и построении графиков функций.
- Плоскую симметрию. Фигура обладает плоской симметрией, если существует плоскость, которая делит ее на две одинаковые половины. Плоская симметрия используется, например, для нахождения дополнительных точек симметрии в треугольниках и прямоугольниках.
- Радиальную симметрию. Фигура обладает радиальной симметрией, если существует точка, называемая центром симметрии, от которой фигура равноудалена во всех направлениях. Радиальная симметрия часто используется при рисовании кругов и окружностей.
Принципы симметрии находят применение в различных областях математики. Например, симметрия используется при решении геометрических задач, при анализе функций и построении графиков, а также при изучении алгебры и теории чисел.
Изучение симметрии помогает развивать логическое мышление и восприятие формы, а также позволяет обнаружить закономерности и связи между различными математическими объектами.
В целом, принципы симметрии в математике играют важную роль и помогают улучшить понимание и визуализацию различных математических концепций. Они также находят применение в других науках, таких как физика, химия и дизайн.
Зачем изучать симметричные фигуры?
Изучение симметричных фигур является важным этапом в математике для детей начальной школы. Знание симметрии поможет им развить важные навыки и умения, а также понимание основных концепций и принципов.
Вот несколько причин, по которым изучение симметричных фигур является полезным:
- Развитие визуального восприятия: изучение симметрии помогает детям развивать способность видеть и понимать визуальные образы. Они учатся распознавать и создавать симметричные фигуры, что способствует развитию их визуального восприятия и пространственного мышления.
- Развитие логического мышления: при изучении симметричных фигур дети учатся применять логическое мышление. Они должны понять и применить правила симметрии, чтобы создавать и распознавать симметричные фигуры. Это развивает их способность рассуждать и решать проблемы.
- Улучшение моторики: изучение симметрии также способствует развитию мелкой моторики и координации движений рук. Дети учатся создавать симметричные фигуры, рисуя и раскрашивая их. Это помогает им улучшить свои навыки рукописи и моторику рук.
- Узнавание и применение симметричных фигур в реальной жизни: симметричные фигуры встречаются повсюду в нашей жизни. Знание симметрии поможет детям распознавать и применять ее в различных ситуациях. Например, они смогут распознать симметричные формы в архитектуре зданий или в природе.
Изучение симметричных фигур не только интересно, но и полезно для развития у детей важных математических навыков, логического мышления и визуального восприятия. При этом они могут видеть применение симметричных фигур в реальной жизни, что делает эту тему еще более практичной и значимой.
Урок информатики во 2 классе «Симметрия»
Тип урока: комбинированный урок с применением ИКТ.
Цели:
-
систематизация знаний учащихся по построению симметричных изображений;
-
закрепление понятий симметричность фигур, ось симметрии;
-
обучение построению симметричных изображений фигур, нахождению оси симметрии некоторых фигур;
-
отработка умений и навыков по основным техническим приемам работы на компьютере;
-
развитие мышления учащихся при отработке умения построения симметричных фигур.
Оборудование: ПК, учебники: Тур С. Н., Бокучава Т. П.. Информатика: 2 класс, СПб: БХВ-Петербург, 2008; изображения фигур.
Программное обеспечение: WindowsXP, Linux, GCompris – математика — Отразить заданный предмет
Ход урока.
-
Организационный момент. (2 мин.)
Здравствуйте!
Начинается урок,
Он пойдёт ребятам впрок,
Постарайтесь всё понять,
Ответы полные давать,
Чтоб за работу получать
Только лишь оценку «пять»!
-
Проверка домашнего задания. (3 мин.)
На прошлом уроке мы говорили о симметричных фигурах, а дома вы должны были нарисовать симметричные предметы. Давайте посмотрим, что у вас получилось. Какие фигуры называют симметричными?
-
Сообщение темы урока. Разминка. (3 мин.)
Сегодня мы продолжим работать с симметричными фигурами: находить их, изображать в тетради и строить с помощью компьютерной обучающей программы.
Игра «Аукцион». Кто больше назовет симметричных предметов, находящихся в нашем кабинете.
Работа с учебником. (7 мин.)
Назовите буквы, у которых есть ось симметрии. (Вспоминаем алфавит и доказываем, есть ли ось симметрии). (А, В, Д, Е, Ж, З, К, Л, М, Н, О, П, С, Т, Ф, Х, Ш, Э, Ю)
Обратите внимание, что у некоторых букв есть две оси симметрии. (Ж, Н, О, Ф, Х)
Придумайте симметричные слова из букв, имеющих ось симметрии. (Оно, Анна, Алла, потоп)
Определите, какая фигура на рисунке «лишняя».
Работа в учебнике-тетради. (7 мин.)
Нарисуйте симметричные изображения букв и слов (отразите букву или слово относительно вертикальной или горизонтальной оси симметрии).
Нарисуйте ось симметрии для каждой фигуры. Дорисуйте каждую фигуру так, чтобы она стала симметричной.
Физминутка. Игра «Зеркало». (3 мин.)
Будь зеркальным отраженьем,
Повторяй мои движенья –
Раз, два, три –
И снова повтори.
Вывод: в зеркале становится все наоборот – правая рука левой, левая нога – правой.
-
Работа с компьютером. (12 мин.)
Упражнение «Отразить заданный предмет».
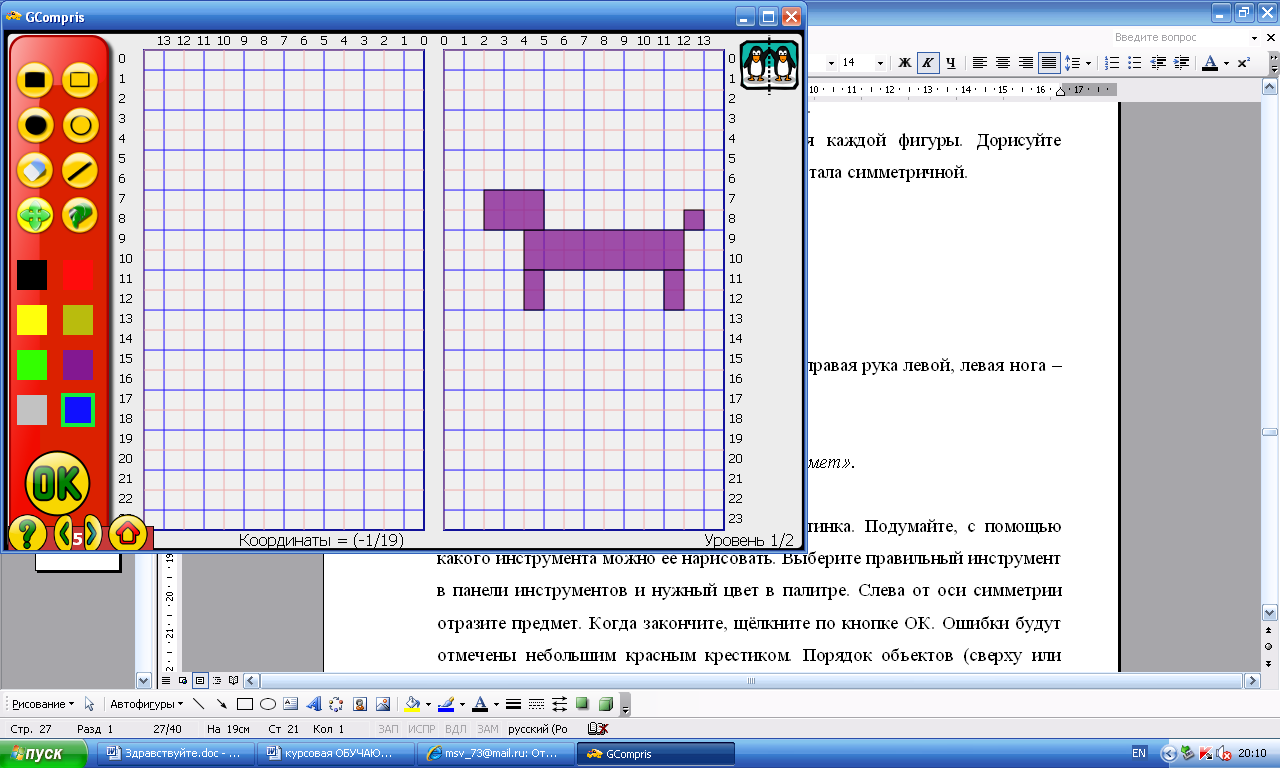
Рисунок 1. Окно программы «Отразить заданный предмет»
В правой части листа изображена картинка. Подумайте, с помощью какого инструмента можно её нарисовать. Выберите правильный инструмент в панели инструментов и нужный цвет в палитре. Слева от оси симметрии отразите предмет. Когда закончите, щёлкните по кнопке ОК. Ошибки будут отмечены небольшим красным крестиком. Порядок объектов (сверху или снизу) не важен, но будьте внимательны, чтобы под объектами не оказалось других ненужных объектов.
-
Итог урока. (5 мин.)
Игра «Сколько осей симметрии?
На доске расположены фигуры (квадрат, равносторонний треугольник, круг, прямоугольный треугольник, прямоугольник, лист дуба, божья коровка, пуговица). Определите, сколько осей симметрии у каждой фигуры. (квадрат -4, равносторонний треугольник — 3, круг — много, прямоугольный треугольник — нет, прямоугольник — 2, лист дуба — 1, божья коровка — 1, пуговица — 2)
— Оценки за урок.
VIII. Домашнее задание. (3мин.)
Нарисуйте в учебнике-тетради листья деревьев, у которых есть ось симметрии.
Осевая симметрия – виды, свойства и примеры фигур
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
Рис. 1 Фигуры, обладающие симметричностью
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
Объект симметричен относительно прямой, если все его точки имеют такие же симметричные аналоги относительно этой прямой. Она же – центр симметрии.
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Рис. 4 Примеры осевой симметрии
Фигуры, имеющие несколько осей симметрии
https://youtube.com/watch?v=mosY_2mbLZk
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
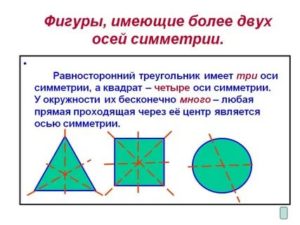
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
«Современная профориентация педагогов и родителей, перспективы рынка труда и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Урок по математике на тему: «Эти симметричные фигуры…» Подготовлен и проведен учителем начальных классов Фалюта Л.В. во 2«А» классе
Ну-ка, проверь, дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка?
Запомните: фигурки, у которых одна половинка как две капли похожа на другую, называют зеркальной симметрией. (ОСЕВОЙ)
Эти фигуры называют симметричными относительно прямой линии, а прямую линию называют осью симметрии.
Достройте вторую половинку нашей работы.
Симметричен человек И увидеть можно: Глаза два и уха два. И руки две- точно! Две ноги и две ноздри, Щечки улыбаются. Симметричен человек, Это всех касается!
Издревле люди стремились украсить все, что окружало их в быту. Они старались простой предмет сделать нарядным, внести праздничность в повседневную жизнь. Украшали дома и ворота, столы и сундуки, орудия труда, посуду и многое другое.
Природа вдохновила человека на создание симметричных форм. Они придумывали удивительные замысловатые орнаменты. В построении орнамента часто используется симметрия. Сегодня на уроке мы будем учиться создавать орнаменты из геометрических фигур с помощью симметрии. СУРПАН- головная повязка
Орнамент – это узор, элементы которого подчинены определенному ритму
Красный – свобода Желтый – цвет солнца Белый – чистота помыслов, честь, благородство
Симметрия – порядок, четкость в изображении
Симметрия – способ создания красоты
Симметрия – способ создания совершенства
Симметрия! Я гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, ты в малой мошке, Ты в елочке, что у лесной дорожки. С тобою в дружбе и тюльпан, и роза, И снежный рой – творение мороза.
Выставка работ учащихся.
http://nikolaeva.21204s01.edusite.ru/p8aa1.html чувашская вышивка http://silova.21411s16.edusite.ru/p26aa1.html чувашская вышивка http://www.bestreferat.ru/referat-113224.html чувашские узоры http://artmus.culture21.ru/ppage.aspx?objid=23031&page=943&type=14&auth=1137&norole=1 чувашский орнамент www.chuvbook.ru учебник чувашского языка, рабочая тетрадь для 2 класс Картинки-раскраски
Курс повышения квалификации
Курс повышения квалификации
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-674766
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Более 50 российских школ перешли на дистанционку из-за коронавируса
Время чтения: 1 минута
Учителям истории предлагают предоставить право бесплатно посещать музеи
Время чтения: 2 минуты
Россияне чаще американцев читают детям страшные и печальные книжки
Время чтения: 1 минута
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Рабочая программа по изучению симметричных фигур
Цель: ознакомить учащихся с понятием симметрии и научить распознавать и строить симметричные фигуры.
1. Введение в понятие симметрии (1 урок)
1.1 Определение симметрии в математике
1.2 Примеры симметричных и несимметричных предметов вокруг нас
1.3 Различение оси симметрии и отсутствия оси симметрии
2. Распознавание симметричных фигур (2 урок)
2.1 Определение симметричной фигуры
2.2 Примеры симметричных фигур
2.3 Практические упражнения по распознаванию симметричных фигур
3. Построение симметричных фигур (2 урок)
3.1 Определение оси симметрии
3.2 Построение оси симметрии с помощью линейки и карандаша
3.3 Практические упражнения по построению симметричных фигур
4. Игра «Найди симметричную фигуру» (1 урок)
4.1 Правила игры
4.2 Практические упражнения по поиску симметричных фигур
5. Подведение итогов и оценка (1 урок)
5.1 Обзор пройденного материала
5.2 Проверочная работа по теме «Симметричные фигуры»
5.3 Оценка успеваемости учащихся
Программа разработана для обучения учащихся 2 класса и может быть адаптирована под специфику каждой группы. Уроки проводятся в игровой форме с использованием различных материалов, включая учебные пособия, задания на распечатках и активное участие детей в упражнениях и играх.
Рабочая тетрадь симметричных фигур для учащихся 2 класса
Рабочая тетрадь по математике для учащихся 2 класса предназначена для изучения симметричных фигур. Эта тетрадь поможет детям развить навыки распознавания и создания симметричных фигур, а также понимания принципов симметрии.
Цель рабочей тетради:
- Познакомить детей с понятием симметрии и ее применением в жизни;
- Развить навыки распознавания и создания симметричных фигур;
- Улучшить восприятие пространственных отношений;
- Способствовать развитию логического мышления.
Структура рабочей тетради:
- Введение в понятие симметрии.
- Упражнения на распознавание симметричных фигур.
- Упражнения на создание симметричных фигур.
- Задачи с использованием симметричных фигур.
- Повторение и закрепление материала.
Основные принципы симметрии, которые изучаются в рабочей тетради:
- Ось симметрии: прямая линия, которая делит фигуру на две равные и зеркальные части.
- Зеркальная симметрия: свойство фигуры, когда она может быть разделена на две симметричные половины относительно оси симметрии.
- Фигуры с несколькими осями симметрии: фигуры, которые могут быть разделены на две или более симметричные части.
Примеры заданий:
| № | Задание |
|---|---|
| 1 | Проследуйте по оси симметрии и закрасьте половину фигуры. |
| 2 | Нарисуйте отражение фигуры относительно указанной оси симметрии. |
| 3 | Подпишите фигуры на картинках, которые симметричные. |
| 4 | Решите задачу, используя знания о симметрии. |
Рабочая тетрадь симметричных фигур для учащихся 2 класса создана для обучения детей разным типам симметрии и развития их математических навыков. Тетрадь содержит интересные и практические задания, которые помогут ученикам лучше понять понятие симметрии и научиться применять его в реальной жизни.
Итог урока
Обобщим полученные знания.
Сегодня на уроке мы познакомились с
двумя основными видами симметрии:
центральная и осевая. Посмотрим на экран
и систематизируем полученные знания.
Обобщающая таблица
|
Осевая |
Центральная |
|
|
Особенность |
Все точки |
Все |
|
Свойства |
1. Симметричные точки лежат на 3. Прямые переходят в прямые, 4. |
1. Симметричные точки лежат на 2. Расстояние от точки до прямой 3. |



























