Вопрос-ответ:
Что такое симметрия в математике?
Симметрия в математике — это свойство фигуры или объекта сохранять свою форму и структуру при некоторых преобразованиях, таких как повороты, отражения или переносы.
Какие бывают виды симметрии в математике?
В математике существует несколько видов симметрии. Одним из них является осевая симметрия, когда фигура делится на две симметричные части относительно оси. Другим видом является центральная симметрия, когда фигура имеет центр, относительно которого она симметрична. Также существуют симметрия относительно плоскости и симметрия относительно точки.
Какие примеры симметрии можно привести?
Примеры симметрии можно найти вокруг нас. Например, лицо человека является симметричным относительно центральной оси — линии, проходящей через нос. Круг является симметричным относительно любого радиуса, а прямоугольник — относительно горизонтальной и вертикальной осей.
Какая роль симметрии в математике?
Симметрия играет важную роль в математике. Она помогает нам классифицировать и анализировать геометрические фигуры и объекты. Симметричные фигуры и структуры часто являются более простыми для изучения и понимания. Кроме того, симметрия используется в различных областях математики, таких как теория групп, топология, фракталы и другие.
Каким образом симметрия применяется в реальной жизни?
Симметрия имеет множество применений в реальной жизни. Например, симметричные фигуры и узоры используются в дизайне, архитектуре и искусстве. Отражение симметрии можно наблюдать в зеркале или в отражении водной поверхности. Симметричные структуры также играют важную роль в биологии, например, в строении растений и животных.
Что такое симметрия в математике?
Симметрия в математике — это свойство фигур, объектов или функций сохранять свою форму, размеры и расположение при определенных преобразованиях. Это означает, что после применения симметричного преобразования объект остается неизменным.
Какие бывают виды симметрии в математике?
В математике выделяют несколько видов симметрии. Это осевая симметрия, центральная симметрия и трансляционная симметрия. Осевая симметрия отражает фигуру относительно некоторой оси, центральная симметрия — относительно некоторой точки, а трансляционная симметрия сдвигает фигуру на некоторое расстояние без изменения ее формы.
Осевая и центральная симметрии. Проводим урок с ЭФУ
Статьи
Линия УМК А. Г. Мерзляка. Математика (5-6)
Математика
Разберемся, как провести урок в 6 классе по теме «Осевая и центральная симметрии» с использованием ЭФУ.
05 февраля 2020
Поурочные разработки к УМК «Математика. 6 класс» А.Г. Мерзляка разработаны в соответствии с основными положениями ФГОС ООО и легли в основу системы уроков, в каждом из которых собрано все необходимое для проведения занятия в шестом классе.
Из курса математики 5 класса учащиеся уже узнали, как выглядят и строятся фигуры, имеющие ось симметрии. Перед изучением темы «Осевая и центральная симметрии» будет целесообразно повторить материал 5 класса. Следует разъяснить учащимся, что построение фигуры во многих случаях возможно по положению ключевых точек.
Учитель: Отрезок можно определить положением концов, треугольник — расположением вершин. Какие еще примеры вы можете назвать? Ученики: Квадрат по 4 точкам, например… И ромб! Учитель: Верно. Чтобы построить фигуру, которая будет симметрична нашему треугольнику или ромбу, нам необходимо отразить ее ключевые точки.
Для закрепления этого интуитивно-наглядного понимания, учитель может предложить детям перегнуть лист бумаги, на котором изображены симметричные фигуры.
Понятие симметрии
Слово «симметрия» происходит от греческого symmetria, что означает соразмерность. В нашем случае, симметрия — это свойство геометрических фигур к отображению.
Учитель: Симметрия используется в рисунках, орнаментах, архитектуре с давних времен. Где еще симметрию могут использовать люди?
Ученики: при строительстве домов; в изготовлении предметов быта.Учитель: верно, но ведь симметрия распространена не только там, где творил человек! Мы видим симметричные объекты природы каждый день. Назовите мне три таких объекта!Ученики: Бабочка, цветы, форма листа! Морская звезда, снежинка, яблоко в разрезе. Симметрий, как это не покажется вам странным и любопытным, много, но мы будем рассматривать две симметрии на плоскости: относительно точки и прямой. Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Заметим, что любые две фигуры, симметричные относительно некоторой прямой, равны (Рис.131). Все точки фигуры, имеющей ось симметрии, не принадлежащие этой оси, можно разделить на пары симметричных точек (Рис. 132).
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Фигуры, имеющие центр симметрии — понятие, воспринимающееся учащимися сложнее, чем фигуры, имеющие ось симметрии. Для удобства восприятия и понимания, рекомендуется привести как можно больше примеров из окружающей природы.
В зависимости от уровня математической подготовки учащихся класса, можно обратить их внимание на то, что прямая — это фигура, имеющая бесконечно много осей и центров симметрии. С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах
Для каждого параграфа в учебнике подобраны задачи для самостоятельного решения. Задания распределены по трем уровням сложности — от простых к трудным. Для дополнительной мотивации учащихся и практического применения полученных знаний предлагается решить специальную задачу «От мудрой совы» — здесь школьникам понадобится проявить смекалку и изобретательность. Еще одна рубрика, которая неизменно заинтересует как юных первооткрывателей, так и учителей, — рубрика «Когда сделаны уроки», в которой можно узнать о важных математических объектах и истории их появления
С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах. Для каждого параграфа в учебнике подобраны задачи для самостоятельного решения. Задания распределены по трем уровням сложности — от простых к трудным. Для дополнительной мотивации учащихся и практического применения полученных знаний предлагается решить специальную задачу «От мудрой совы» — здесь школьникам понадобится проявить смекалку и изобретательность. Еще одна рубрика, которая неизменно заинтересует как юных первооткрывателей, так и учителей, — рубрика «Когда сделаны уроки», в которой можно узнать о важных математических объектах и истории их появления.
Предложите ребятам решить задание № 1260. Какие печатные буквы русского алфавита имеют 1) вертикальную ось симметрии; 2) горизонтальную ось симметрии; 3) горизонтальную и вертикальную оси?
Готовый яркий раздаточный материал «Алфавит» вы можете скачать в конце этой статьи.
Также рекомендуем вам применять на уроке различные методы преподнесения информации: как визуальный, так и аудио. Попробуйте аудиодиктант.
Симметрия
С древних времен люди стремятся упорядочить мир вокруг себя. Поэтому что-то считается красивым, а что-то не очень. С эстетической точки зрения как привлекательные рассматриваются золотое и серебряное сечения, а также, разумеется, симметрия. Этот термин имеет греческое происхождение и дословно означает «соразмерность». Разумеется, речь идет не только о совпадении по этому признаку, но также и по некоторым другим. В общем смысле симметрия — это такое свойство объекта, когда в результате тех или иных образований результат равен исходным данным. Это встречается как в живой, так и в неживой природе, а также в предметах, сделанных человеком.
Прежде всего термин «симметрия» употребляется в геометрии, но находит применение во многих научных областях, причем его значение остается в общем и целом неизменным. Это явление достаточно часто встречается и считается интересным, поскольку различается несколько его видов, а также элементов. Использование симметрии также интересно, ведь она встречается не только в природе, но и в орнаментах на ткани, бордюрах зданий и многих других рукотворных предметах. Стоит рассмотреть это явление поподробнее, поскольку это крайне увлекательно.
Урок «Осевая и центральная симметрия»
Краткое описание документа:
Симметрия – достаточно интересная тема в геометрии, так как именно это понятие очень часто встречается не только в процессе жизнедеятельности человека но и в природе.
Первая часть видео-презентации «Осевая и центральная симметрия» дает определение симметричности двух точек относительно прямой на плоскости. Условием их симметричности является возможность проведения через них отрезка, через середину которого будет проходить заданная прямая. Обязательным условием такой симметричности является перпендикулярность отрезка и прямой.
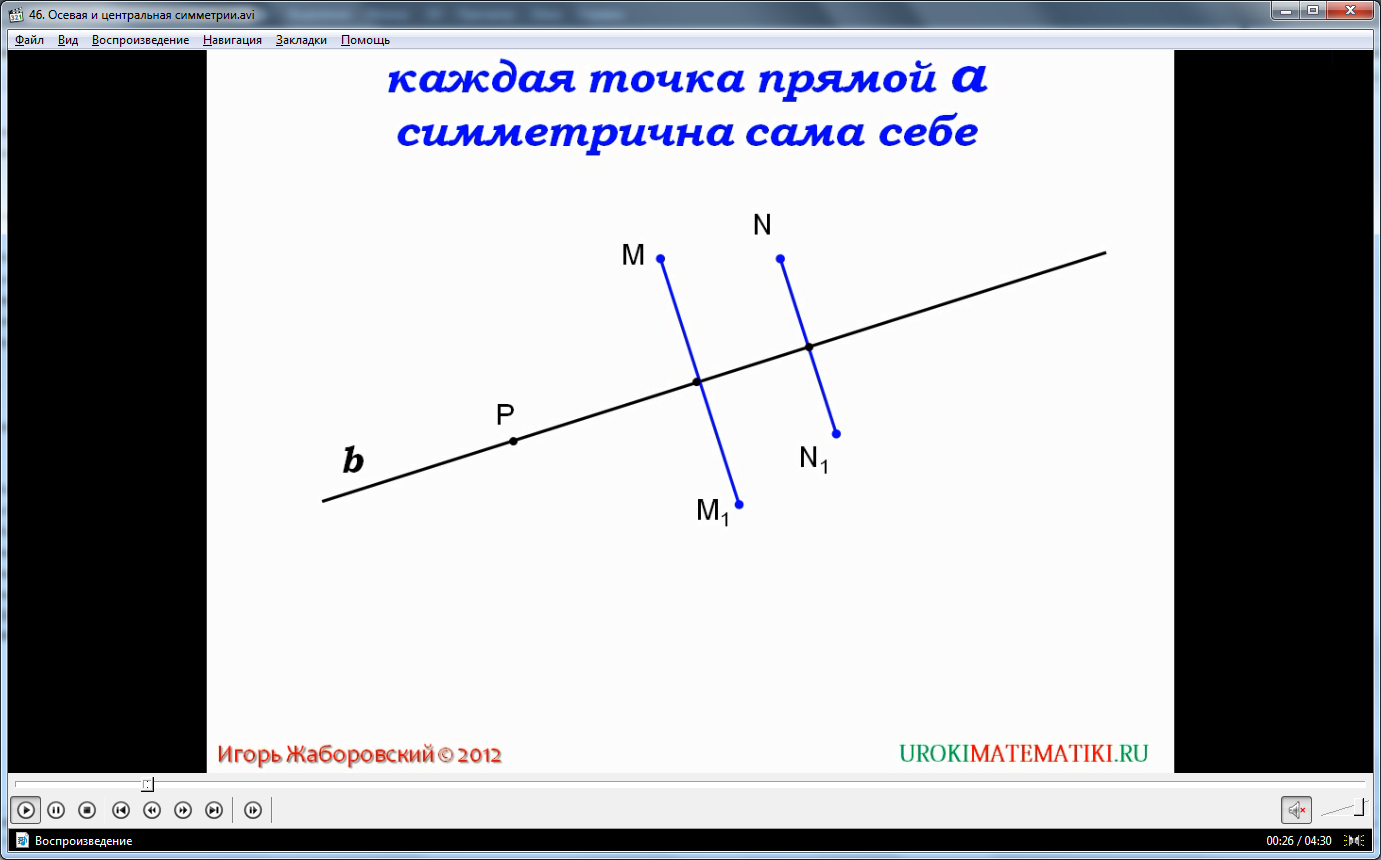
Следующая часть видео-урока дает наглядный пример определения, который показывается в виде чертежа, где несколько пар точек симметричны относительно прямой, а любая точка на этой прямой симметрична сама себе.
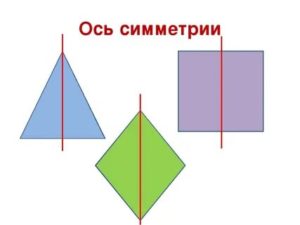
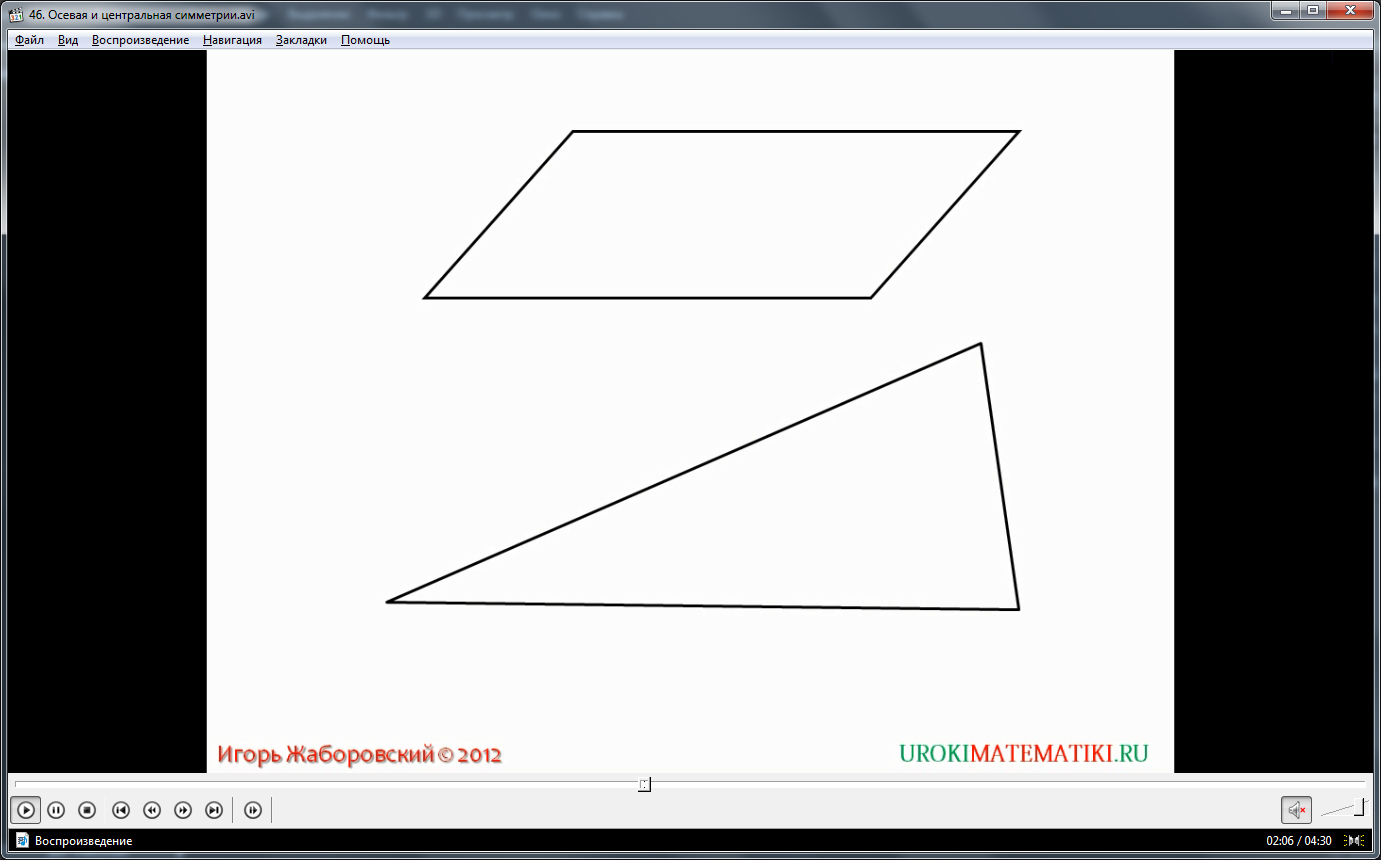
После получения первоначальных понятий о симметрии, ученикам предлагается более сложное определение фигуры, симметричной относительно прямой. Определение предлагается в виде текстового правила, а также параллельно сопровождается речью диктора за кадром. Завершает эту часть примеры симметричных и не симметричных фигур, относительно прямой. Интересно, что существуют геометрические фигуры, имеющие несколько осей симметрии – все они наглядно представлены в виде чертежей, где оси выделены отдельным цветом. Облегчить понимание предлагаемого материала можно таким способом – предмет или фигура является симметричной, если она точно совпадает при складывании двух половин относительно своей оси.
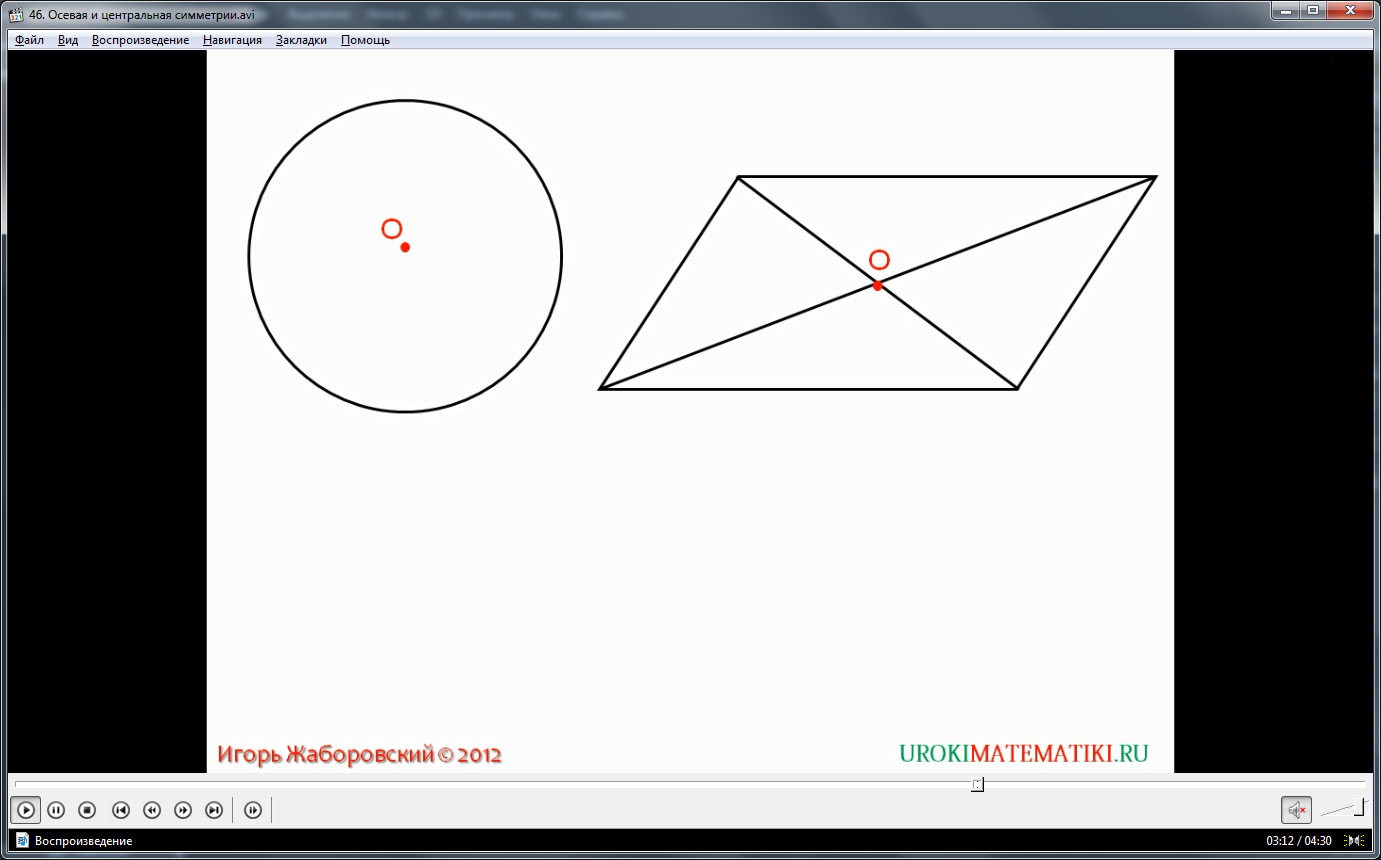
Кроме осевой симметрии существует симметрия относительно одной точки. Именно этому понятию посвящена следующая часть видео-презентации. Сначала дается определение симметричности двух точек относительно третьей, затем предоставляется пример в виде рисунке, где показаны симметричная и не симметричная пара точек. Завершает эту часть урока примеры геометрических фигур, у которых присутствует или отсутствует цент симметрии.
В заключении урока ученикам предлагается ознакомиться с наиболее яркими примерами симметрии, которые можно встретить в окружающем мире. Понимание и умение строить симметричные фигуры просто необходимы в жизни людей, которые занимаются самыми разными профессиями. По своей сути симметрия – основа всей человеческой цивилизации, так как 9 из 10 предметов, окружающих человека, имеют тот или иной тип симметрии. Без симметрии было бы не возможно возведение многих больших архитектурных сооружений, не получилось бы достигнуть впечатляющих мощностей в промышленности и так далее. В природе симметрия также – очень распространенное явление, и если в неодушевленных предметах ее встретить практически невозможно, то живой мир буквально кишит ею – практически вся флора и фауна, за редким исключением, имеет или осевую, или центральную симметрию.
Обычная школьная программа разрабатывается с таким учетом, чтобы ее мог бы понять любой ученик, допущенный к занятием
Видео-презентация в несколько раз облегчает этот процесс, так как одновременно воздействует на несколько центров освоения информации, предоставляет материал в нескольких цветах, тем самым, заставляя учеников концентрировать внимание учеников на самом важном во время урока. В отличии от обычного способа обучения в школах, когда не каждый учитель имеет возможность или желание отвечать ученикам на уточняющие вопросы, видео-урок легко можно перемотать на необходимое место, чтобы заново прослушать диктора и прочитать нужную информацию еще раз, вплоть до ее полного понимания. Учитывая простоту подачи материала, видео-презентацию можно использовать не только во время школьных занятий, но и в домашних условиях, в качестве самостоятельного способа обучения
Учитывая простоту подачи материала, видео-презентацию можно использовать не только во время школьных занятий, но и в домашних условиях, в качестве самостоятельного способа обучения.
urokimatematiki.ru
1.3. Поворотная симметрия
Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … В этом случае о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.
Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой.
Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».
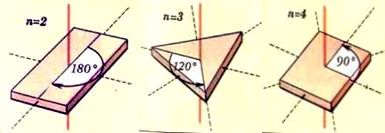
На рисунке 2.7. даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.
Как найти ось симметрии в фигурах
Ось симметрии — это линия, которая делит фигуру на две симметричные половины. Если сложить эти половины, они полностью совпадут.
В 3 классе дети начинают учиться искать ось симметрии в простых геометрических фигурах. Для этого используются следующие правила:
- Нарисуйте фигуру на листе бумаги.
- Поставьте ручку или карандаш на прямой линии или стороне фигуры.
- Проверьте, совпадают ли две части фигуры, они должны быть зеркальными отражениями друг друга.
- Если фигура имеет более одной оси симметрии, повторите шаги 2 и 3 для каждой линии.
Некоторые фигуры, такие как прямоугольники и квадраты, имеют оси симметрии, проходящие через центр фигуры. Другие фигуры, например, треугольники и прямоугольные треугольники, могут иметь оси симметрии, проходящие через стороны.
Отметьте найденные оси симметрии на фигуре. Это поможет визуально представить ось симметрии и лучше понять концепцию.
Примеры фигур и их осей симметрии:
Фигура
Оси симметрии
Прямоугольник
Оси симметрии проходят через центр по диагоналям
Квадрат
4 оси симметрии проходят через центр по диагоналям и сторонам
Треугольник
3 оси симметрии проходят через центр по медианам
Прямоугольный треугольник
3 оси симметрии проходят через стороны
Поиск оси симметрии в фигурах помогает детям развивать умение анализировать и сравнивать формы, а также понимать принципы симметрии
Это является важной навыком в изучении геометрии и визуального искусства
Количество осей симметрии
У количество будет различным. Например, у круга и шара таких осей множество. У равностороннего треугольника осью симметрии будет перпендикуляр, опущенный на каждую из сторон, следовательно, у него три оси. У квадрата и прямоугольника можно провести четыре оси симметрии. Две из них перпендикулярны сторонам четырехугольников, а две другие являются диагоналями. А вот у равнобедренного треугольника ось симметрии только одна, располагающаяся меду равными его сторонами.
Осевая симметрия встречается и в природе. Ее можно наблюдать в двух вариантах.
Первый вид – радиальная симметрия, предполагающая наличие нескольких осей. Она характерна, например, для морских звезд. Более высокоразвитым организмам присуща билатеральная, или двусторонняя симметрия с единственной осью, делящей тело на две части.
Человеческому телу тоже присуща билатеральная симметрия, но идеальной ее назвать нельзя. Симметрично расположены ноги, руки, глаза, легкие, но не сердце, печень или селезенка. Отклонения от билатеральной симметрии заметны даже внешне. Например, крайне редко бывает так, чтобы у человека на обеих щеках были одинаковые родинки.
«Симметрия
» в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.
По более точному определению симметрия
– это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости). Подавляющее большинство кристаллов обладает симметрией.
Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии
, ось симметрии
, центр симметрии
, или центр инверсии
.
Плоскость симметрии делит кристалл на две зеркально равные части. Обозначается она буквой Р. Части, на которые плоскость симметрии рассекает многогранник, относятся одна к другой, как предмет к своему изображению в зеркале разные кристаллы имеют различное количество плоскостей симметрии, которое ставится перед буквой Р. Наибольшее количество таких плоскостей у природных кристаллов – девять 9Р. В кристалле серы насчитывается 3Р, а у гипса только одна. Значит, в одном кристалле может быть несколько плоскостей симметрии. В некоторых кристаллах плоскость симметрии отсутствует.
Относительно элементов ограничения плоскость симметрии может занимать следующее положение:
- проходит через ребра;
- лежать перпендикулярно к ребрам в их серединах;
- проходить через грань перпендикулярно к ней;
- пересекать гранные углы в их вершинах.
В кристаллах возможны следующие количества плоскостей симметрии: 9Р, 7Р, 6Р, 5Р, 4Р, 3Р, 2Р, Р, отсутствие плоскости симметрии.
Увлекательная симметрия геометрических фигур: сколько у них осей?
Геометрические фигуры являются фундаментальными элементами в мире математики и обладают множеством характеристик, которые делают их интересными и увлекательными. Одной из таких характеристик является симметрия, которая означает точное соответствие между частями фигуры, разделенной пополам осью. В этой статье мы рассмотрим симметрию геометрических фигур и сосредоточимся на вопросе: сколько у них осей?
Симметрия в геометрических фигурахСимметрия – это свойство, определяющее взаимосвязь между частями геометрической фигуры. Фигура считается симметричной, если ее можно разделить на две равные части с помощью оси симметрии. Эта ось может быть вертикальной, горизонтальной или даже диагональной, в зависимости от рассматриваемой фигуры.
Оси симметрии в основных фигурахНаиболее распространенные основные геометрические фигуры, такие как квадрат, прямоугольник, треугольник и круг, имеют разное количество осей симметрии. Далее перечислим количество осей симметрии для каждой из этих фигур:
- Квадрат: имеет 4 оси симметрии: две вертикальные и две горизонтальные.
- Прямоугольник: также имеет 4 оси симметрии: две вертикальные и две горизонтальные.
- Равносторонний треугольник: имеет 3 оси симметрии: одну вертикальную и две диагонали.
- Круг: хотя на первый взгляд кажется, что он не имеет осей симметрии, на самом деле он имеет бесконечные оси симметрии, поскольку любая линия, проходящая через центр круга, разделит его на две равные части.
Оси симметрии в более сложных фигурах.По мере продвижения к более сложным фигурам количество осей симметрии может увеличиваться или уменьшаться. Например, правильный шестиугольник имеет 6 линий симметрии, а правильный пятиугольник — только 5. В целом, правильные геометрические фигуры имеют тенденцию иметь большее количество линий симметрии по сравнению с неправильными фигурами.
Для некоторых фигур может быть сложно определить точное количество линий симметрии без проведения точных расчетов или измерений.
Влияние осей симметрии на фигуры: детальный анализ
Оси симметрии являются фундаментальными элементами геометрических фигур, поскольку они оказывают существенное влияние на их внешний вид и на наше восприятие. В этом подробном анализе мы рассмотрим, как линии симметрии влияют на фигуры и как их можно использовать для создания эстетически приятных и сбалансированных дизайнов.
Определение оси симметрииОсь симметрии — это воображаемая линия, делящая фигуру на две одинаковые части, подобно зеркалу. Эта линия может быть вертикальной, горизонтальной или диагональной, в зависимости от фигуры.
Значение осей симметрии на рисункахОси симметрии оказывают существенное влияние на фигуры, поскольку создают ощущение баланса и визуальной гармонии. Когда фигура имеет ось симметрии, две части, генерируемые по обе стороны от оси, являются точным отражением друг друга. Это создает ощущение порядка и стабильности в рисунке.
Применение осей симметрииОси симметрии имеют различное применение в разных областях. В архитектуре, например, их используют для создания симметричных фасадов, передающих ощущение солидности и красоты. В дизайне логотипов линии симметрии используются для создания простого и запоминающегося дизайна. В искусстве оси симметрии используются для создания сбалансированных и привлекательных композиций.
Типы осей симметрииСуществует три основных типа осей симметрии: вертикальная, горизонтальная и диагональная. Вертикальная ось симметрии делит фигуру на две одинаковые части по обе стороны от оси. Горизонтальная ось симметрии делит фигуру на две одинаковые части: одну над осью, другую снизу. Диагональная ось симметрии делит фигуру на две одинаковые части, по одной с каждой стороны оси.
Примеры фигур с осями симметрииМногие геометрические фигуры имеют линии симметрии.
Эврика! Теперь, когда вы знаете все о линиях симметрии, вы готовы стать королем геометрии. Теперь вы можете ходить и говорить что-то вроде: «Я мастер симметрии!» или «Мои линии симметрии прямее линейки!»
Но будьте осторожны, не зацикливайтесь на симметрии и начните раскладывать картофель фри на тарелке по размеру. Помните, что симметрия — это лишь одно из многих чудес, которые может предложить геометрия.
Так что продолжайте исследовать увлекательный мир форм и форм и никогда не забывайте, что симметрия есть повсюду, от бабочки до вашего собственного лица (хотя, возможно, вы предпочитаете не думать об этом слишком много).
До следующих геометрических приключений, любитель симметрии! И не забывайте, что красота геометрии – в глазах смотрящего (и в осях симметрии, конечно).
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.

А сколько примеров окружает нас постоянно! Это цветы, листья, лепестки, овощи и фрукты, животные и даже соты пчел имеют ярко выраженную геометрическую форму и симметрию. Вся природа устроена упорядоченно, всему есть свое место, что еще раз подтверждает совершенство законов природы, в которых симметрия — основное условие.
Аритмия
Этот термин, прежде всего, напоминает большинству о медицине и кардиологии, однако он изначально имеет несколько другое значение. В данном случае синонимом будет «асимметрия», то есть отсутствие или нарушение регулярности в том или ином виде. Ее можно встретить как случайность, а иногда она может стать прекрасным приемом, например, в одежде или архитектуре. Ведь симметричных зданий очень много, но знаменитая чуть наклонена, и хоть она не одна такая, но это самый известный пример. Известно, что так получилось случайно, но в этом есть своя прелесть.
Кроме того, очевидно, что лица и тела людей и животных тоже не полностью симметричны. Проводились даже исследования, согласно результатам которых «правильные» лица расценивались как неживые или просто непривлекательные. Все-таки восприятие симметрии и это явление само по себе удивительны и пока не до конца изучены, а потому крайне интересны.
Осевая симметрия
article>ÐÐ¾Ñ ÐºÐ°Ðº звÑÑÐ¸Ñ Ð¾Ð¿Ñеделение оÑевой ÑиммеÑÑии:
ÐÑевой ÑиммеÑÑией назÑваеÑÑÑ ÑиммеÑÑиÑ, пÑÐ¾Ð²ÐµÐ´ÐµÐ½Ð½Ð°Ñ Ð¾ÑноÑиÑелÑно пÑÑмой. ÐÑи оÑевой ÑиммеÑÑии лÑбой ÑоÑке, ÑаÑположенной по Ð¾Ð´Ð½Ñ ÑÑоÑÐ¾Ð½Ñ Ð¿ÑÑмой, вÑегда ÑооÑвеÑÑÑвÑÐµÑ Ð´ÑÑÐ³Ð°Ñ ÑоÑка на вÑоÑой ÑÑоÑоне ÑÑой пÑÑмой.
ÐÑи ÑÑом оÑÑезки, ÑоединÑÑÑие ÑÑи ÑоÑки, пеÑпендикÑлÑÑÐ½Ñ Ð¾Ñи ÑиммеÑÑии.
Ðа ÑиÑÑÐ½ÐºÐ°Ñ Ð¾ÑÐµÐ²Ð°Ñ ÑиммеÑÑиÑ: ÑоÑки A и B ÑиммеÑÑиÑÐ½Ñ Ð¾ÑноÑиÑелÑно пÑÑмой a; ÑоÑки R и F ÑиммеÑÑиÑÐ½Ñ Ð¾ÑноÑиÑелÑно пÑÑмой AB 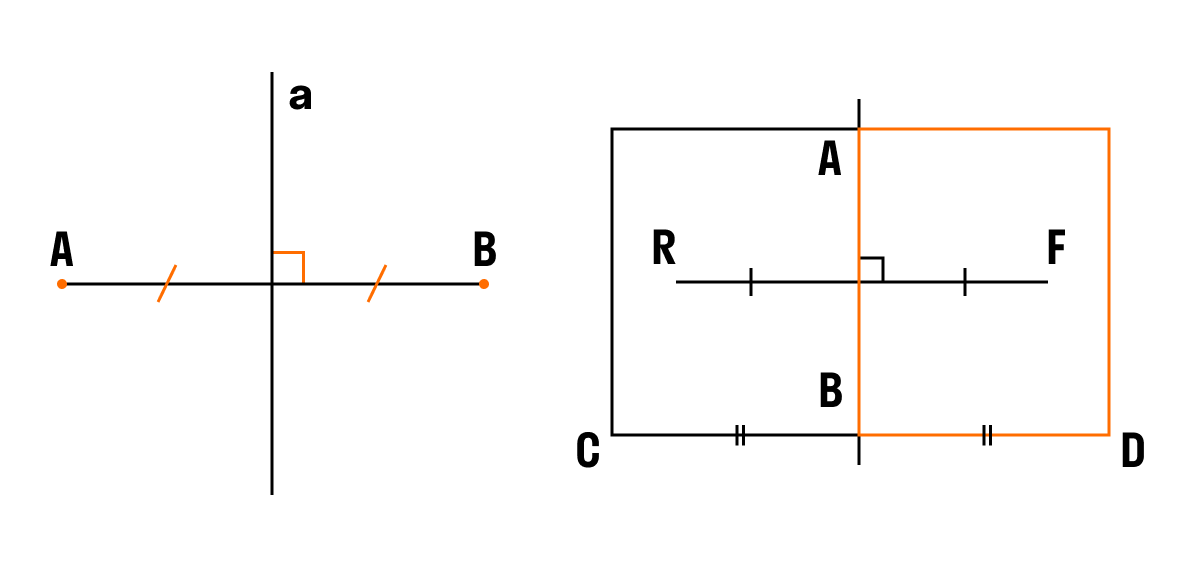
ÐÑÐµÐ²Ð°Ñ ÑиммеÑÑÐ¸Ñ ÑаÑÑо вÑÑÑеÑаеÑÑÑ Ð² повÑедневной жизни. Ð ÑожалениÑ, не на ÑоÑо в паÑпоÑÑе и не в ÑÑÑÐµÐ»ÐºÐ°Ñ Ð½Ð° глазаÑ. Ðо ÐµÑ Ð²Ð¿Ð¾Ð»Ð½Ðµ Ñебе можно вÑÑÑеÑиÑÑ Ð² Ð¿Ð¾Ð»Ð¾Ð²Ð¸Ð½ÐºÐ°Ñ Ð°Ð²Ð¾ÐºÐ°Ð´Ð¾, на моÑде коÑа или в зданиÑÑ Ð²Ð¾ÐºÑÑг. ÐÑÐµÐ²Ð°Ñ ÑиммеÑÑÐ¸Ñ â неоÑÑÐµÐ¼Ð»ÐµÐ¼Ð°Ñ ÑаÑÑÑ Ð°ÑÑиÑекÑÑÑÑ. ÐглÑдиÑеÑÑ Ð¸ поиÑиÑе пÑимеÑÑ Ð¾Ñевой ÑиммеÑÑии вокÑÑг ваÑ.

РгеомеÑÑии еÑÑÑ ÑигÑÑÑ, обладаÑÑие оÑевой ÑиммеÑÑией: квадÑаÑ, ÑÑеÑголÑник, Ñомб, пÑÑмоÑголÑник.
ÐавайÑе ÑазбеÑемÑÑ, как поÑÑÑоиÑÑ ÑигÑÑÑ, ÑиммеÑÑиÑнÑÑ Ð´Ð°Ð½Ð½Ð¾Ð¹ оÑноÑиÑелÑно пÑÑмой.
ÐÑÐ¸Ð¼ÐµÑ 1. ÐоÑÑÑойÑе ÑÑеÑголÑник A1B1C1 ,ÑиммеÑÑиÑнÑй ÑÑеÑголÑÐ½Ð¸ÐºÑ ABC оÑноÑиÑелÑно пÑÑмой.
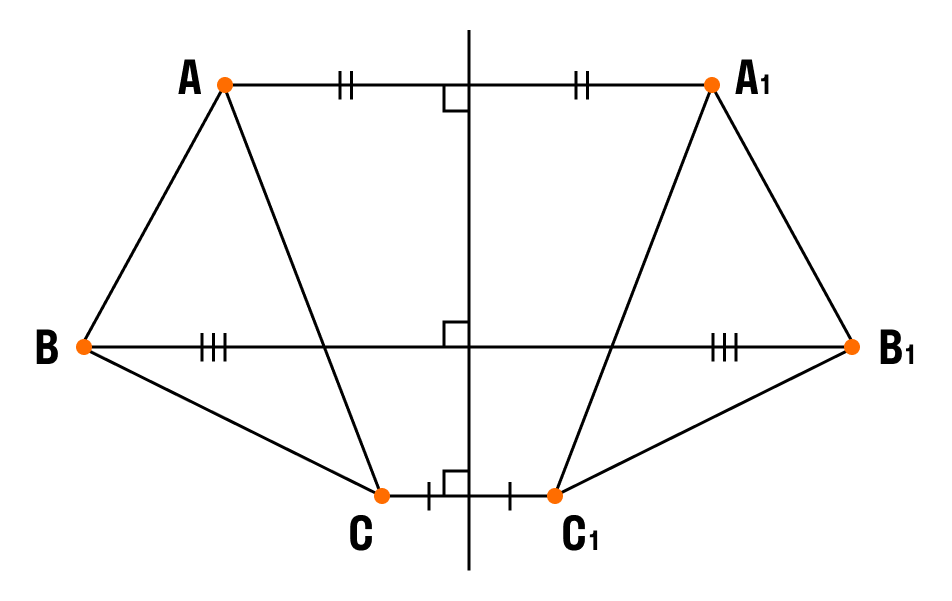
- ÐÑоведем из веÑÑин ÑÑеÑголÑника ABC ÑÑи пÑÑмÑе, пеÑпендикÑлÑÑнÑе оÑи ÑиммеÑÑии, вÑведем ÑÑи пÑÑмÑе на дÑÑгÑÑ ÑÑоÑÐ¾Ð½Ñ Ð¾Ñи ÑиммеÑÑии.
- Ðайдем ÑаÑÑÑоÑние Ð¾Ñ Ð²ÐµÑÑин ÑÑеÑголÑника ABC до ÑоÑек на оÑи ÑиммеÑÑии.
- С дÑÑгой ÑÑоÑÐ¾Ð½Ñ Ð¿ÑÑмой оÑложим Ñакие же ÑаÑÑÑоÑниÑ.
- СоединÑем ÑоÑки оÑÑезками и ÑÑÑоим ÑÑеÑголÑник A1B1C1, ÑиммеÑÑиÑнÑй ÑÑеÑголÑÐ½Ð¸ÐºÑ ABC.
- ÐолÑÑаем два ÑÑеÑголÑника, ÑиммеÑÑиÑнÑÑ Ð¾ÑноÑиÑелÑно оÑи ÑиммеÑÑии.
ÐÑÐ¸Ð¼ÐµÑ 2. ÐоÑÑÑойÑе ÑÑеÑголÑник, ÑиммеÑÑиÑнÑй ÑÑеÑголÑÐ½Ð¸ÐºÑ ABC оÑноÑиÑелÑно пÑÑмой d.
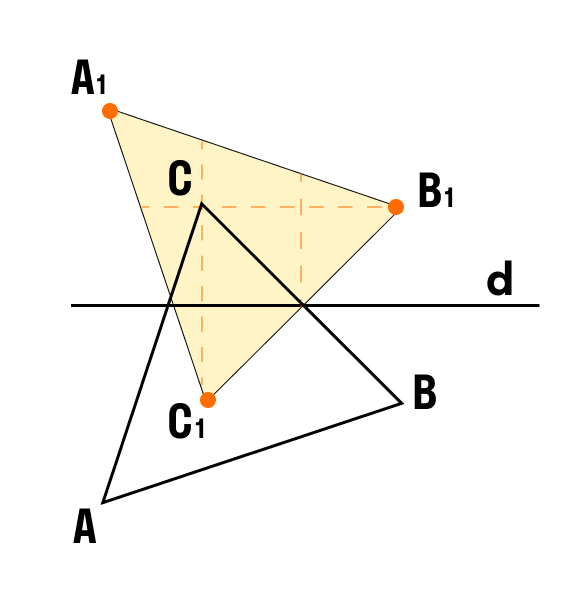
- СÑÑоим по Ñже извеÑÑÐ½Ð¾Ð¼Ñ Ð°Ð»Ð³Ð¾ÑиÑмÑ. ÐÑоводим пÑÑмÑе, пеÑпендикÑлÑÑнÑе пÑÑмой d, из веÑÑин ÑÑеÑголÑника ABC и вÑводим Ð¸Ñ Ð½Ð° дÑÑгÑÑ ÑÑоÑÐ¾Ð½Ñ Ð¾Ñи ÑиммеÑÑии.
- ÐзмеÑÑем ÑаÑÑÑоÑние Ð¾Ñ Ð²ÐµÑÑин до ÑоÑек на пÑÑмой.
- ÐÑкладÑваем Ñакие же ÑаÑÑÑоÑÐ½Ð¸Ñ Ð½Ð° дÑÑгой ÑÑоÑоне оÑи ÑиммеÑÑии.
- СоединÑем ÑоÑки и ÑÑÑоим ÑÑеÑголÑник A1B1C1.
ÐÑÐ¸Ð¼ÐµÑ 3. ÐоÑÑÑоиÑÑ Ð¾ÑÑезок A1B1, ÑиммеÑÑиÑнÑй оÑÑÐµÐ·ÐºÑ AB оÑноÑиÑелÑно пÑÑмой l.
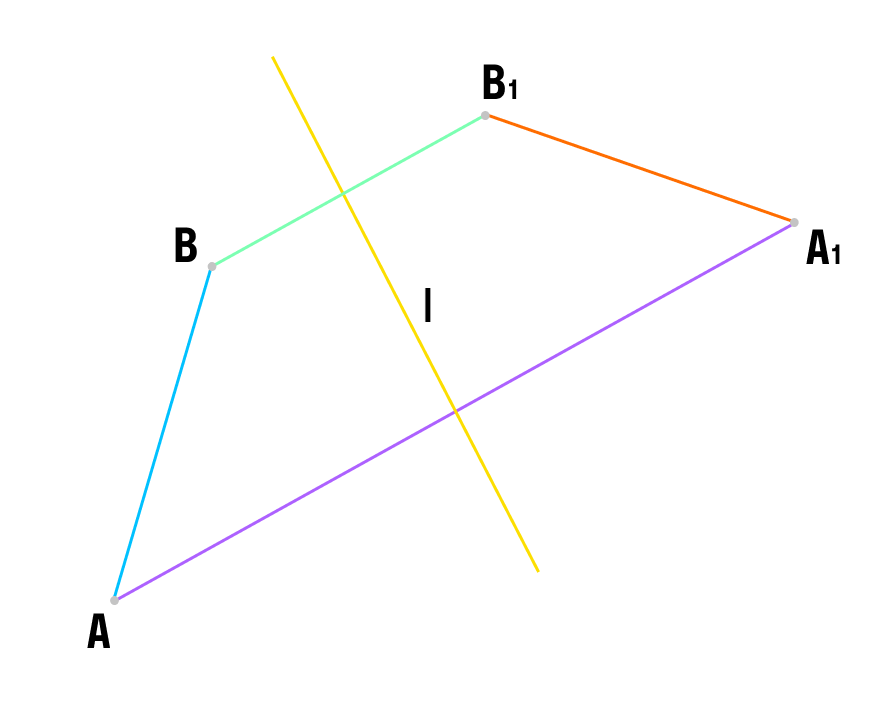
- ÐÑоводим ÑеÑез ÑоÑÐºÑ Ð Ð¿ÑÑмÑÑ, пеÑпендикÑлÑÑнÑÑ Ð¿ÑÑмой l.
- ÐÑоводим ÑеÑез ÑоÑÐºÑ Ð Ð¿ÑÑмÑÑ, пеÑпендикÑлÑÑнÑÑ Ð¿ÑÑмой l.
- ÐзмеÑÑем ÑаÑÑÑоÑÐ½Ð¸Ñ Ð¾Ñ ÑоÑек Ри Рдо пÑÑмой l.
- ÐÑкладÑваем Ñакое же ÑаÑÑÑоÑние на пеÑпендикÑлÑÑнÑÑ Ð¿ÑÑмÑÑ Ð¾Ñ Ð¿ÑÑмой l по дÑÑгÑÑ ÑÑоÑÐ¾Ð½Ñ Ð¸ ÑÑавим ÑоÑки A1 и B1.
- СоединÑем ÑоÑки A1 и B1.
ÐолÑÑе пÑимеÑов и ÑвлекаÑелÑнÑÑ Ð·Ð°Ð´Ð°Ð½Ð¸Ð¹ â
на кÑÑÑÐ°Ñ Ð¿Ð¾ маÑемаÑике в онлайн-Ñколе Skysmart!


























