Калькуляторы и электронные устройства
Калькуляторы и электронные устройства широко применяются для вычислений тангенса и других тригонометрических функций. Современные калькуляторы, как физические, так и программные, обычно имеют встроенную функцию вычисления тангенса, а также других тригонометрических функций, что делает их очень удобными для работы с этими функциями.
Калькуляторы могут иметь различные клавиши для ввода угла в градусах или радианах, и клавишу для вычисления тангенса. После ввода угла калькулятор выдает значение тангенса на дисплее. В программных калькуляторах такая функция также доступна с помощью соответствующего меню или команды.
Кроме калькуляторов, существует множество других электронных устройств, которые могут вычислять тангенс. Например, это могут быть электронные счетчики, компьютеры, смартфоны и другие портативные устройства. Многие из них имеют встроенные калькуляторы, что позволяет с легкостью решать задачи, связанные с тангенсом и другими тригонометрическими функциями.
| Устройство | Описание | Преимущества |
|---|---|---|
| Физический калькулятор | Портативное устройство с клавишами и дисплеем для вычислений | Удобство использования вне компьютерной среды |
| Программный калькулятор | Приложение на компьютере или смартфоне для вычислений | Возможность использования на различных устройствах |
| Электронный счетчик | Устройство для измерения электрических параметров | Высокая точность измерений тангенса |
| Компьютер | Устройство для обработки и хранения данных | Возможность использования специализированных программ для вычисления тангенса |
| Смартфон | Мобильное устройство с широкими возможностями | Портативность и простота использования |
С использованием калькуляторов и электронных устройств, вычисление тангенса становится проще и быстрее
Они позволяют получать точные значения функции, что особенно важно при решении различных математических задач
Как пользоваться таблицами Брадиса
Рассмотрим таблицу Брейдиса для синуса и косинуса. Все, что связано с носовыми пазухами, находится вверху и слева. Если нам нужен косинус, мы смотрим на правую часть внизу таблицы.
Чтобы найти значения синуса угла, найдите пересечение строки, содержащей искомое количество градусов в крайней левой ячейке, и столбца, содержащего искомое количество минут, в самой верхней ячейке.
Если точного значения угла нет в таблице Брадиса, прибегаем к поправкам. Поправки за одну, две и три минуты приведены в крайних правых столбцах таблицы. Чтобы найти значение синуса угла, которого нет в таблице, находим ближайшее значение. После этого добавляем или вычитаем поправку, соответствующую разнице между углами.
Если мы ищем синус угла больше 90 градусов, то надо сначала воспользоваться формулами приведения, а уж потом — таблицей Брадиса.
Пример. Как пользоваться таблицей Брадиса
Пусть требуется найти синус угла 17°44′. По таблице находим тождественный синус 17°42′ и прибавляем изменение его значения за две минуты:
17°44′-17°42’=2′ (требуется поправка) sin 17°44’=0,3040+0,0006=0,3046
Принцип работы с косинусами, тангенсами и котангенсами одинаков
Однако важно помнить о знаке поправок
Важно!
При вычислении значений синуса поправка имеет положительный знак, а при вычислении косинуса поправку необходимо брать с отрицательным знаком.
Синус, косинус и тангенс
Тригонометрия — это ветвь математики, которая занимается изучением углов и взаимосвязей между углами и сторонами треугольников.В этом разделе блога мы будем обсуждать три фундаментальных тригонометрических соотношения: синус, косинус и касательный.Эти соотношения используются для расчета взаимосвязи между углами и сторонами прямоугольного треугольника.
С математической точки зрения три тригонометрические соотношения определяются следующим образом:
1. Синус: синус угла определяется как отношение длины стороны, противоположной углу к длине гипотенузы треугольника.
2. Косинус: косинус угла определяется как отношение длины соседней стороны к длине гипотенузы треугольника.
3. ТАНГАНТА: касание угла определяется как отношение длины боковой напротив угла до длины соседней стороны треугольника.
Эти соотношения важны, потому что они позволяют нам рассчитать длину одной стороны прямоугольного треугольника, если мы знаем длину другой стороны и размер одного из углов.
1. Соотношение синуса:
Соотношение синуса используется для расчета длины боковой напротив угла в прямоугольном треугольнике.Соотношение синуса представлено как грех, где находится угол.Формула для расчета соотношения синуса составляет:
Sin = противоположность/гипотенуза
Например, если у нас есть прямоугольный треугольник с углом 30 градусов и гипотенузой 10 см, мы можем рассчитать длину противоположной стороны, используя отношение синуса:
Sin30 = противоположный/10
Напротив = sin30 x 10
Напротив = 5 см
2. Соотношение косинуса:
Соотношение косинуса используется для расчета длины соседней стороны угла в прямоугольном треугольнике.Соотношение косинуса представлено как cos, где находится угол.Формула для расчета косинусного соотношения:
Cos = прилегающая/гипотенуза
Например, если у нас есть прямоугольный треугольник с углом 45 градусов и гипотенуза 8 см, мы можем рассчитать длину соседней стороны, используя соотношение косинуса:
Cos45 = прилегающий/8
Прилегающий = cos45 x 8
Прилегающий = 5,66 см (округлен до двух десятичных знаков)
3. Соотношение касательного:
Коэффициент касательной используется для расчета длины боковой напротив угла в прямоугольном треугольнике.Коэффициент касательной представлен как загар, где находится угол.Формула для расчета касательной коэффициенты:
Tan = противоположный/прилегающий
Например, если у нас есть прямоугольный треугольник с углом 60 градусов и соседней стороны 6 см, мы можем рассчитать длину противоположной стороны, используя отношение касательной:
Tan60 = наоборот/6
Напротив = tan60 x 6
Напротив = 10,39 см (округлен до двух десятичных знаков)
Коэффициенты синуса, косинуса и касательной являются фундаментальными тригонометрическими соотношениями, которые используются для расчета взаимосвязи между углами и сторонами прямоугольного треугольника.Эти соотношения важны во многих областях, включая инженерию, физику и математику.Знание того, как использовать эти соотношения, важно для тех, кто изучает тригонометрию или использует их в своей профессии. Синус, косинус и тангенс — Тригонометрия: Form4 Тригонометрия: навигационные углы и соотношения
Синус, косинус и тангенс — Тригонометрия: Form4 Тригонометрия: навигационные углы и соотношения
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Синус, косинус, тангенс и котангенс: основные формулы

Формулы приведения
По этим формулам значение тригонометрической функции аргумента a, где p/2 < a < 2p, можно привести к значению функции аргумента a, где 0 < a < p/2, как той же, так и дополнительной к ней.
| Аргумент b
Функция |
– a | + a | p – a | p + a | + a | + a | 2p – a |
| sin b | cos a | cos a | sin a | –sin a | –cos a | –cos a | –sin a |
| cos b | sin a | –sin a | –cos a | –cos a | –sin a | sin a | cos a |
Поэтому в таблицах тригонометрических функций даются значения только для острых углов, причем достаточно ограничиться, например, синусом и тангенсом. В таблице даны только наиболее употребительные формулы для синуса и косинуса. Из них легко получить формулы для тангенса и котангенса. При приведении функции от аргумента вида kp/2 ± a, где k – целое число, к функции от аргумента a:
- название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
- знак в правой части совпадает со знаком приводимой функции в точке kp/2 ± a, если угол a острый.
Например, при приведении ctg (a – p/2) убеждаемся, что a – p/2 при 0 < a < p/2 лежит в четвертом квадранте, где котангенс отрицателен, и, по правилу 1, меняем название функции: ctg (a – p/2) = –tg a.
sin (ab) = sin a cos b cos a sin b;
cos (ab) = cos a cos b sin a sin b
Формулы кратных углов
Эти формулы выводятся прямо из формул сложения:
sin 2a = 2 sin a cos a;
cos 2a = cos2a – sin2a = 2 cos2a – 1 = 1 – 2 sin2 a;
sin 3a = 3 sin a – 4 sin3a;
cos 3a = 4 cos3a – 3 cos a;
Формулу для cos 3a использовал Франсуа Виет при решении кубического уравнения. Он же впервые нашел выражения для cos na и sin na, которые позже были получены более простым путем из формулы Муавра.
Если в формулах двойного аргумента заменить a на a/2, их можно преобразовать в формулы половинных углов.
Формулы универсальной подстановки
Используя эти формулы, выражение, включающее разные тригонометрические функции от одного и того же аргумента, можно переписать как рациональное выражение от одной функции tg (a/2), это бывает полезно при решении некоторых уравнений.
Формулы преобразования сумм в произведения и произведений в суммы.
До появления компьютеров эти формулы использовались для упрощения вычислений. Расчеты производились с помощью логарифмических таблиц, а позже – логарифмической линейки, т.к. логарифмы лучше всего приспособлены для умножения чисел, поэтому все исходные выражения приводили к виду, удобному для логарифмирования, т.е. к произведениям, например:
2 sina sin b = cos (a – b) – cos (a + b);
2 cos a cos b = cos (a – b) + cos (a + b);
2 sin a cos b= sin (a – b) + sin (a + b).
Формулы для функций тангенса и котангенса можно получить из вышеприведенных.
Формулы понижения степени
Из формул кратного аргумента выводятся формулы:
| sin2a = (1 – cos 2a)/2; | cos2a = (1 + cos 2a)/2; |
| sin3a = (3 sin a – sin 3a)/4; | cos3a = (3 cosa + cos 3a)/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
| (tg x)` = ; | (ctg x)` = – ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.
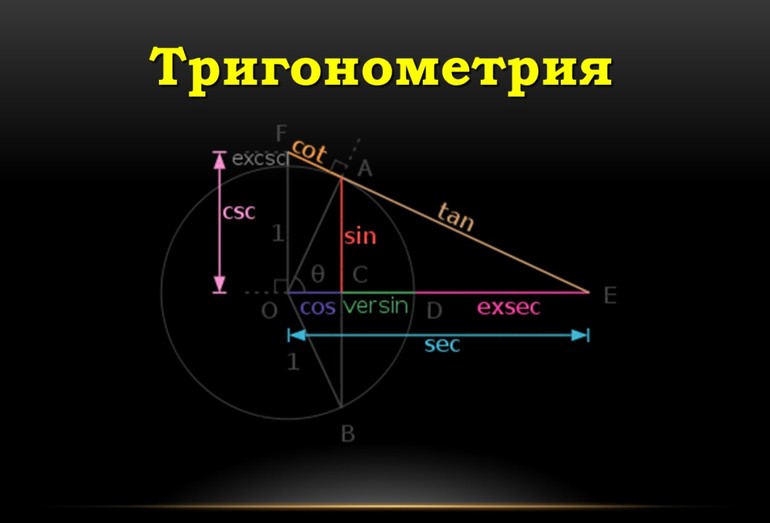
Общая информация
Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.
https://youtube.com/watch?v=9dHBBrXC5uk
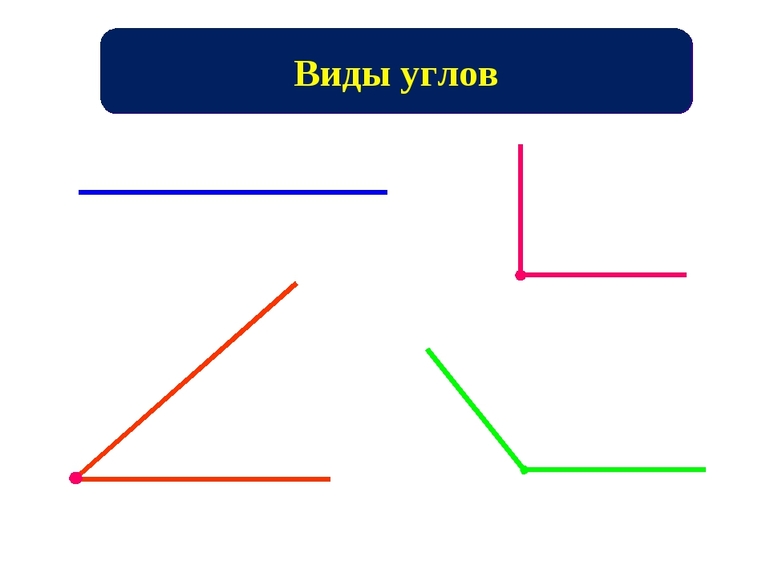
Виды углов
Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.
Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.
Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:
- При х < 90 угол считается острым.
- Если х = 90, то является прямым.
- В случае, когда выполняется неравенство, он считается тупым: 90 < x < 180.
- Развернутый: х = 180.
- Выпуклый: 180 < x < 360.
- Полный: х = 360.
- Свыше 360: x > 360.
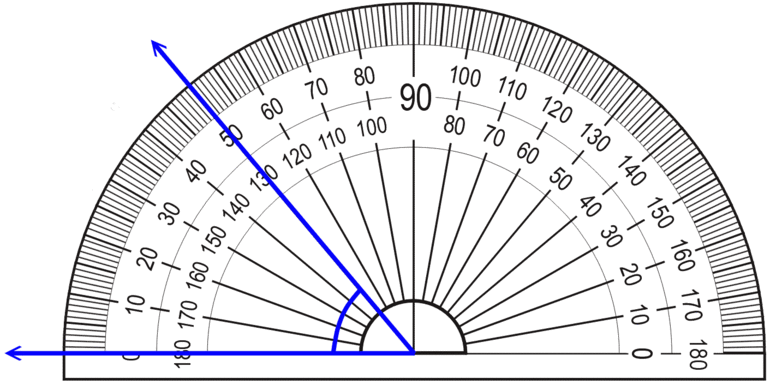
Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
- В радианы: P = (a * ПИ) / 180.
- В градусы: а = (P * 180) / ПИ.
Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.
https://youtube.com/watch?v=trzH5KPEgpw
Смысл функций
Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.

Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.
Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.
График синуса и косинуса
Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .
Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).
Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.
Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.
Мы знаем, что
sin 0 = 0
sin π/6 = 1/2
sin π/2 = 1
Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:
С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:
Теперь соединим их плавной кривой:
Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:
Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:
Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:
В результате мы получили кривую, которую называют синусоидой.
Теперь построим график косинуса. Мы знаем что
cos 0 = 1
cos π/3 = 1/2
cos π/2 = 1
Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:
Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:
Соединяем эти точки плавной линией:
Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:
Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :
Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.
В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:
sin (x+ 2π) = sinx
cos (x+ 2π) = sinx
В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие
f(x) = – f(– x)
Если f(x) – четная ф-ция, то должно выполняться условие:
f(x) = f(– x)
Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:
Поэтому верны формулы:
sin (– α) = – sinα
cos (– α) = cosα
Котангенс на тригонометрической окружности
Чтоб определить котангенс любого угла нам опять не обойтись без системы координат с тригонометрической окружностью. Проведем еще одну ось через точку (0; 1) параллельную оси X и абсолютно такую же как ось X, только называется она уже линией котангенсов. Затем проведем луч AB и из точки B опустим перпендикуляр BC из точки B на ось X.
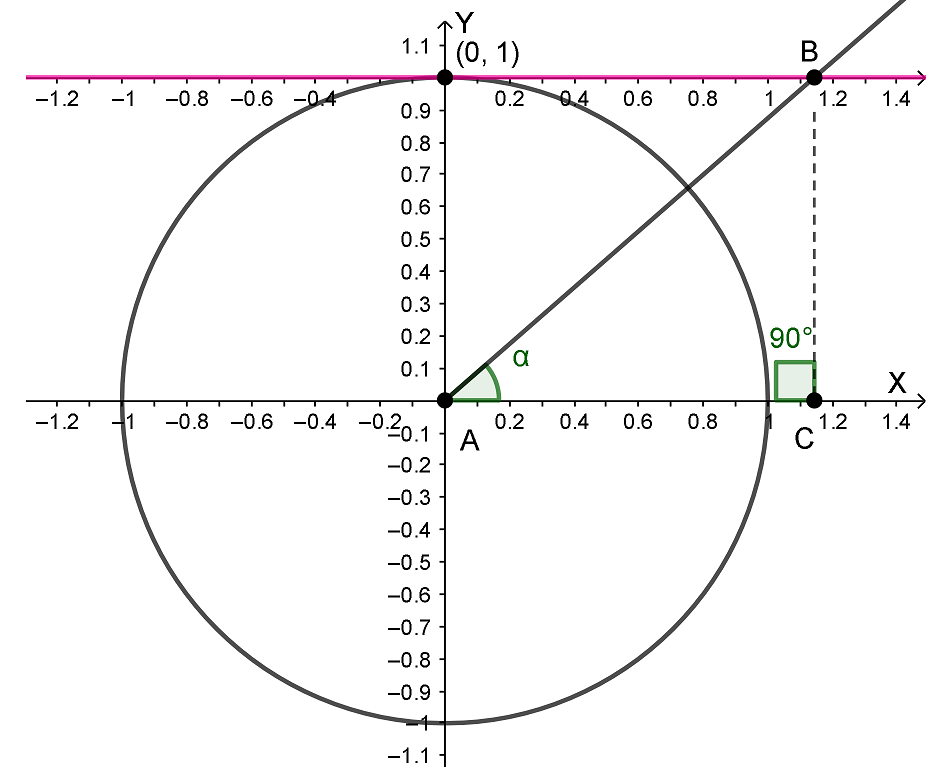
И у нас опять получился прямоугольный треугольник ABC, где угол BAC назовем α.
Из определения котангенса для острых углов известно: чтоб получить котангенс угла α нужно прилежащую к углу α длину стороны AC разделить на длину противолежащей к углу α стороны BC:
Очевидно, что при любом α длина стороны BC, как и радиус окружности, всегда равна единице, тогда:
А при делении на единицу ничего не изменится, значит
Т.е. котангенс угла α будет равен длине отрезка AC.
Не трудно заметить, что при любом α длина стороны AC полностью совпадает с положительной координатой точки B на линии котангенсов. А значит, ctg α будет всегда равен еще и координате точки B на линии котангенсов при всех α. Стороной AC будет не очень удобно пользоваться, поэтому вместо нее возьмем координату точки B на линии котангенсов. Именно эта координата точки B и будет являться котангенсом угла α.
Попробуем приближенно вычислить ctg 150°. Построим систему координат, начертим на ней единичную окружность, проведем линию котангенсов, отмерим угол 150°, проведем луч соответствующий этому углу.
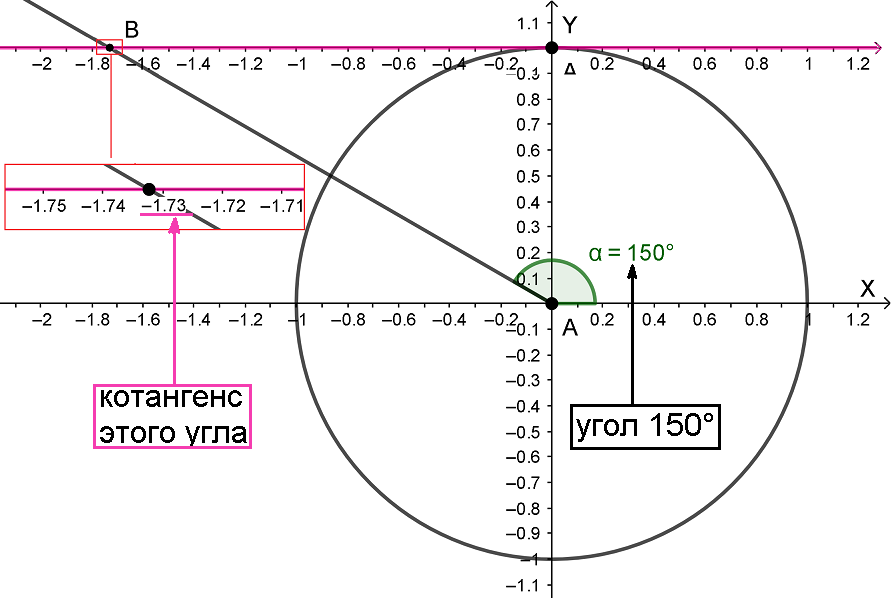
Луч AB пересек линию котангенсов на отметке -1,73, значит ctg 150° ≈ -1,73 (точно: ctg 150° = ).
На калькуляторе нет котангенса. Чтобы вычислить ctg 150°, надо 1 разделить на tg 150°.
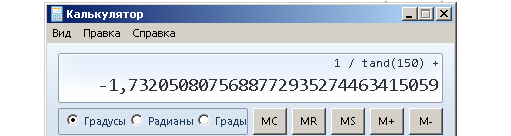
Осталось только определить котангенс для углов от 180° до 360°. Но этой линии котангенсов уже не хватает, поэтому начертим вторую линию котангенсов, проходящую через точку (0; -1), параллельную оси X, но направленную в противоположную сторону.
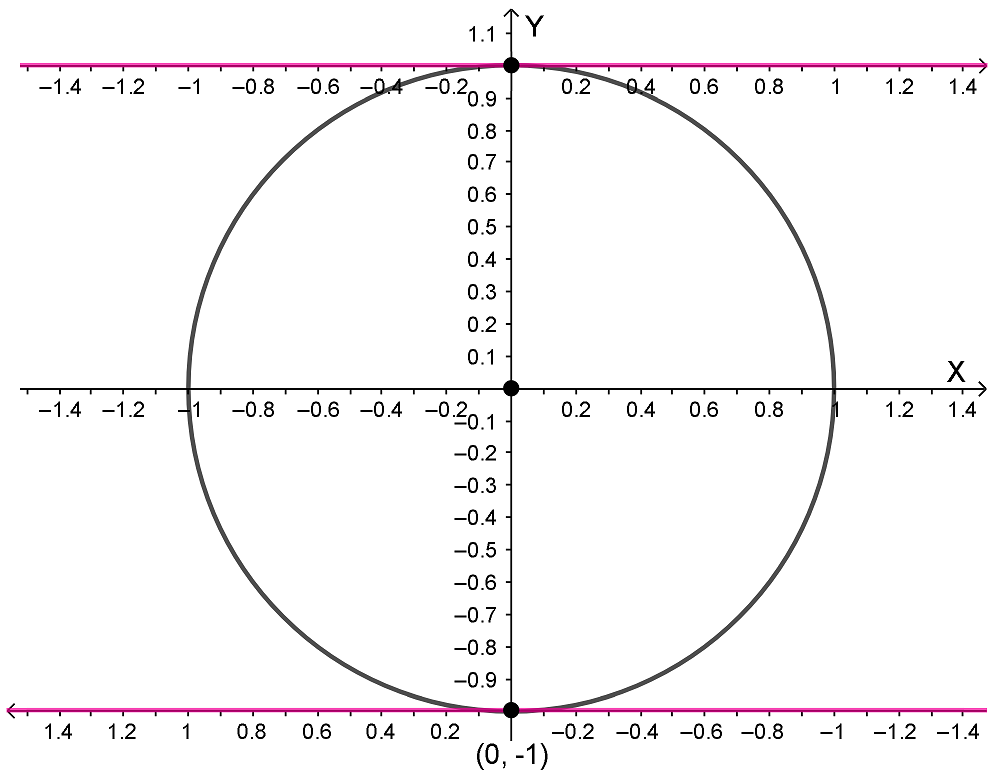
Координата пересечения второй линии котангенсов с лучом AB тоже будет равна котангенсу угла.
Рассмотрим на это на примере. Пусть требуется приближенно вычислить ctg 300°. На системе координат с единичной окружностью проведем луч AB так, чтобы угол α был равен 300°. Тогда луч AB пересечет вторую линию котангенсов где-то на числе -0,58. Значит, ctg 300° ≈ -0,58. Число -0,58 нам уже встречалось – это же , а значит ctg 300° = .
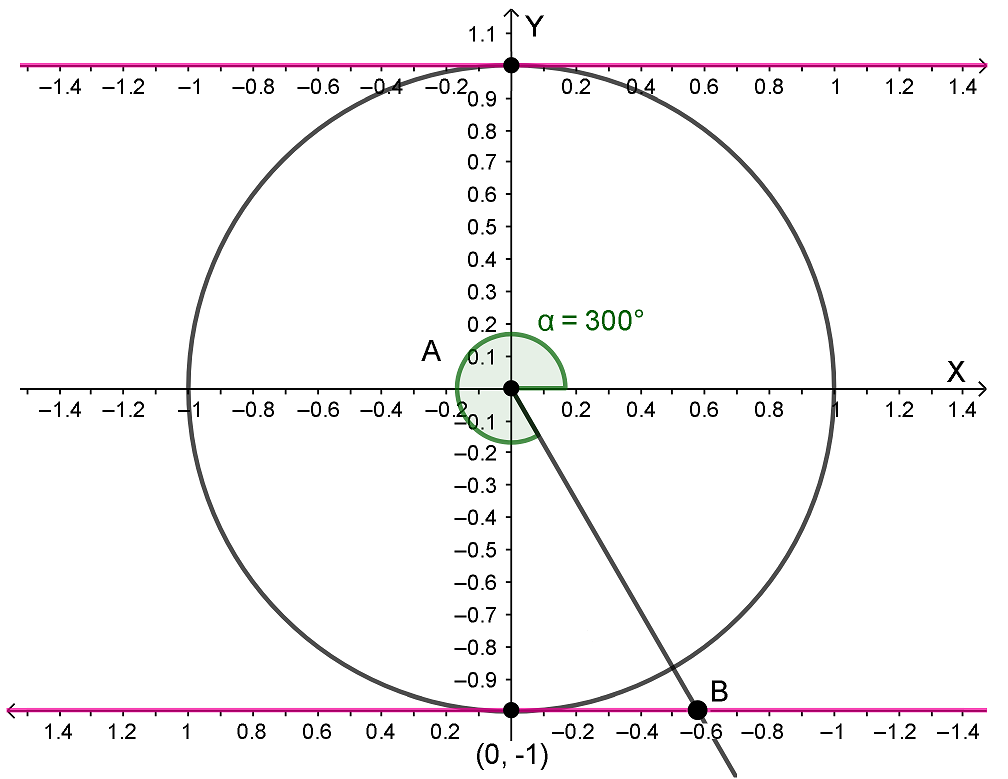
Если сравнить наш результат с калькулятором, то выяснится, что отклонение незначительное. Напоминаю: сначала вычисляем на калькуляторе tg 300°, запоминаем этот результат, затем один делим на число, которое запомнили — получаем ctg 300°.
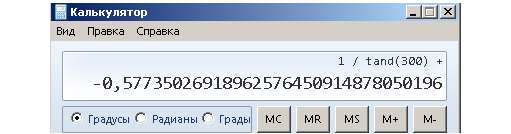
И калькулятор тоже так думает.
Теперь можно обобщить все полученные знания, изобразив на единичной окружности все линии тангенсов и котангенсов и уже точные значения всех нужных углов этих функций.
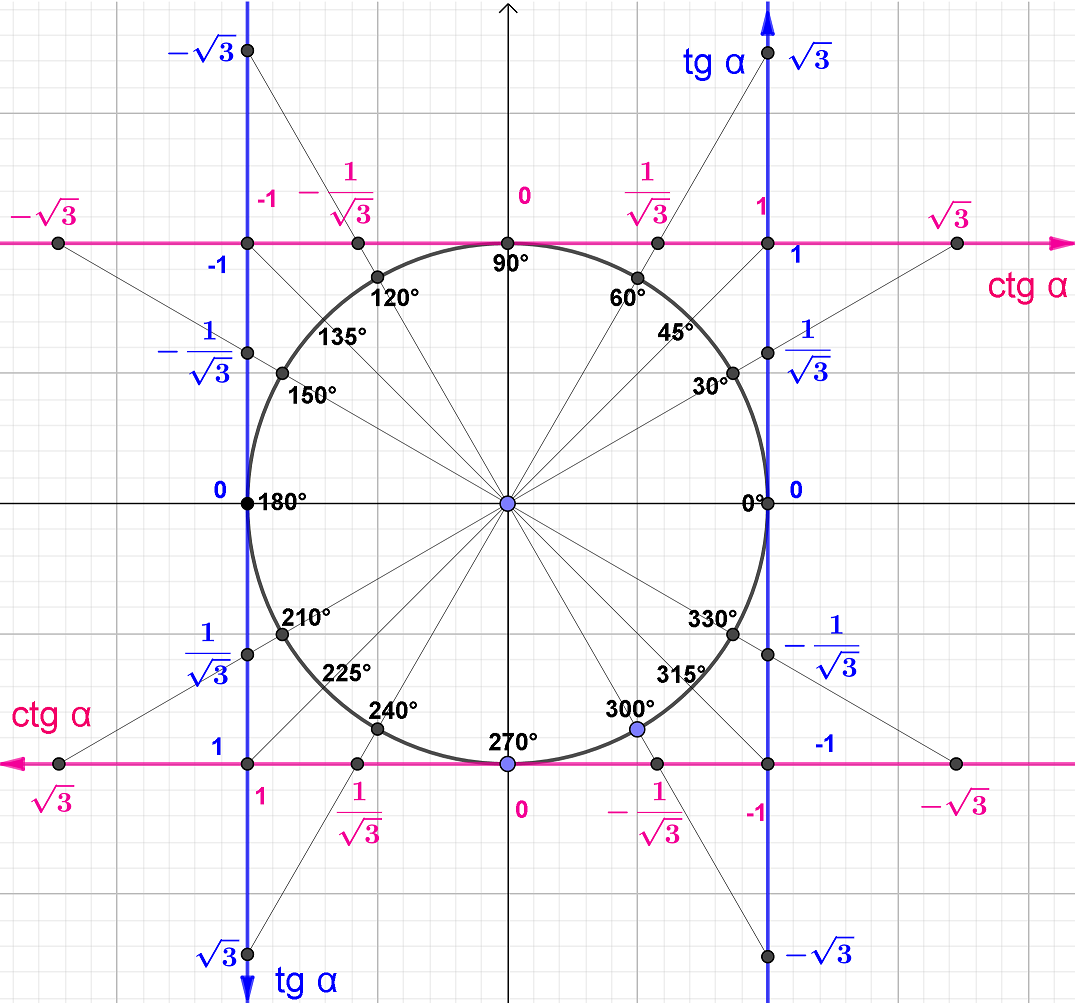
Чтобы определить тангенс или котангенс любого угла от 0° до 360°, достаточно на единичной окружности провести луч, соответствующий требуемому углу, и посмотреть в точке с какой координатой этот луч пересечет одну из линий тангенсов или котангенсов, эта координата и будет равна тангенсу или котангенсу требуемого угла.
Теперь, благодаря тригонометрической окружности, можно легко заметить многие свойства тангенса и котангенса, не прикладывая особых усилий. Например, если плавно увеличивать угол α от 0° до 90°, то tg α будет также возрастать, и чем больше угол α приближается к 90°, тем быстрее увеличивается его тангенс. Аналогично будет увеличиваться и ctg α, если α уменьшать от 90° до 0° или уменьшать от 270° до 180°. Уже можно увидеть, что tg 0° = 0, tg 180° = 0, ctg 90° = 0 и ctg 270° = 0. Настоятельно рекомендую убедиться во всем этом самостоятельно.
Следует обратить особое внимание, что когда угол α равен 90° или 270°, луч AB будет параллелен линиям тангенсов и не пересечет ни одну из них, поэтому тангенсов этих углов не существует, их вообще невозможно определить, выражения tg 90° и tg 270° не имеют смысла, как и деление на ноль. Также, когда угол ал равен 0° или 180° луч AB не пересечет линии котангенсов, значит сtg 0° и tg 180° не существует.. Определить все точные значения этих функций школьными методами нельзя, но это и не понадобится
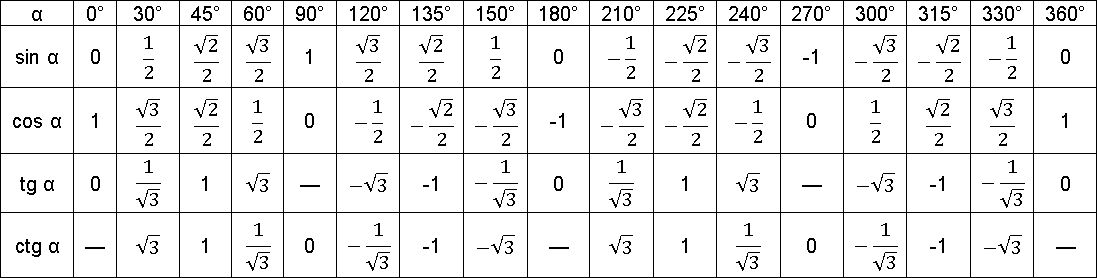
Нужно знать только точные значения тангенса и котангенса углов, изображенных на предыдущем рисунке, но запомнить их в таком виде будет гораздо проще чем таблицу, изображенную ниже, да и без единичной окружности не получится решить многие другие задачи.
Определить все точные значения этих функций школьными методами нельзя, но это и не понадобится. Нужно знать только точные значения тангенса и котангенса углов, изображенных на предыдущем рисунке, но запомнить их в таком виде будет гораздо проще чем таблицу, изображенную ниже, да и без единичной окружности не получится решить многие другие задачи.