Математика

Алгебра: уравнения, функции и графики

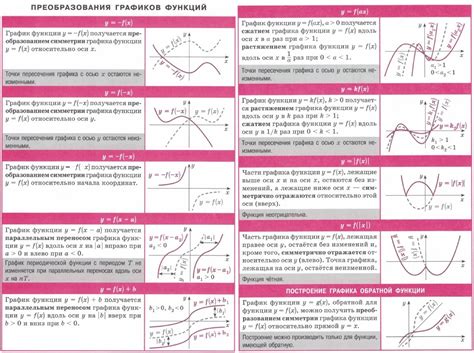
В алгебре изучаются математические выражения, уравнения, функции и графики. Алгебра является одной из основных областей математики и является важным инструментом во многих научных и инженерных дисциплинах.

Одной из основных задач алгебры является решение уравнений. Уравнение представляет собой математическое выражение, содержащее один или несколько неизвестных, для которых требуется найти значения, удовлетворяющие заданному условию. Например, уравнение x + 5 = 10 имеет решением x = 5.

Функции являются основным понятием в алгебре. Функция — это правило, которое сопоставляет каждому элементу множества одно и только одно значение из другого множества. Функции могут быть заданы различными способами, например, аналитически (через формулу), графически (с помощью графика) или таблично (через таблицу значений).

Графики являются важной частью алгебры. График функции представляет собой геометрическую интерпретацию функции в виде точек на координатной плоскости

Это позволяет наглядно представить зависимость между переменными и анализировать поведение функции в различных точках. Графики могут быть использованы для нахождения решений уравнений, определения экстремумов функций, поиска пересечений и т.д.

С помощью алгебры можно решать множество задач, как теоретических, так и практических. Она находит применение в различных областях знания, таких как физика, экономика, компьютерные науки и другие. Понимание основных принципов алгебры позволяет анализировать и решать сложные проблемы в различных областях деятельности.

Математические загадки с подвохом, математические загадки для детей с ответами

Не все так серьезно и скучно в математике, как может показаться на первый взгляд. Предлагаю немножко поиграться с числами, отгадывая веселые математические загадки от Пустунчика. Но не торопись с ответом — в каждом вопросе есть подвох.

34
66 т.

Можешь предложить
занимательное математическое соревнование
одноклассникам. Поделитесь на две
команды (или играйте каждый сам за себя)
и начинайте отгадывать на скорость.
Интересно, кто из вас заслужит почетное
звание математического гения?

Как говорится, Бог в
помощь, ветер в паруса. Начали!

1. Ехал как-то мотоциклист
в город. По дороге ему повстречались
пять легковых автомобилей и грузовик.
Сколько машин ехало в город?

2. Было в одной семье
два отца и два сына. Сколько это человек?

3. Мальчик купил книгу
с оберткой за 11 гривен. За саму книгу он
заплатил на 10 гривен больше стоимости
обертки. Назовите отдельную цену книги
и обертки.

4. Жили-были пять сыновей,
и у каждого из них была сестра. Посчитайте,
сколько же детей в семье?

5. Два хороших товарища
вышли навстречу друг другу: первый из
пункта А со скоростью 20 км/ч, а второй
из пункта В со скоростью 15 км/ч. Кто из
них будет ближе к пункту А, когда друзья
встретятся.

6. Одно яйцо варится 4
минуты, сколько времени нужно варить
шесть яиц?

7. Есть 4 яблока. Подели
их, не разрезая, между тремя друзьями
таким образом, чтобы никто из друзей не
получил больше чем остальные.

8. Часы с
боем отбивают 1 удар за 1 секунду. За
какое время они отобьют 12 часов?

Ответы:

1. Как минимум одна.

2. Три человека: дед,
отец и сын.

3. Обертка стоила 50
копеек, а книга — 10 гривен 50 копеек.

4. Шесть детей.

5. Они встретятся на
одинаковом расстоянии от пункта А.

6. Четыре минуты (или
немножко больше).

7. Два яблока даем одному
другу, и по одному — двум другим.

8. За 11 секунд.

Вот такая вот арифметика
для малышей. Признайся честно, сколько
из этих вопросов удалось осилить Тебе?

Заметили орфографическую ошибку? Выделите её мышкой и нажмите Ctrl+Enter

Вопрос о материи и о точности

В богословских терминах (что чрезвычайно далеко от Мейясу, позиционирующего себя как антифидеиста) пифагорейскую теорию можно сформулировать так: Бог сотворил математику и некоторое количество материи. Поэтому материя подчиняется математическим законам. Что-то им должно подчиняться, в чем-то они должны воплощаться. Таким образом, мы выходим из пифагореизма в теорию Аристотеля о формах и материи.

Остается вопрос, можно ли назвать теорию Аристотеля дуализмом формы и материи, если материя только «есть», и ничего больше о ней сказать нельзя. На мой взгляд, это дуализм, но тут можно рассуждать по-разному.

В истории философии было много дуалистических учений, где материи явным образом приписываются те или иные свойства. В учении Декарта материя уже обладает полным набором свойств. Не факт, что такой тип дуализма будет востребован в онтологии будущего. А вот аристотелевский дуализм, как мне кажется, очень подходит для современных учений, которые выделяют структуру отдельно от ее воплощения. И именно материя ответственна за воплощение структуры и представление ее в реальности.

Тегмарк формулирует эту идею следующим образом: чтобы описать математическую структуру вселенной, нам надо мысленно избавиться от так называемого багажа. Под багажом понимается конкретное воплощение структуры. В некотором смысле у Тегмарка получается, что багажом является материя. Однако он имеет в виду не это, а то, что багаж мешает выделять структуры

Он отвлекает внимание на себя. А это значит, что у него есть собственное бытие, то есть, скорее всего, какая-то своя структура

Однако не исключено, что слишком простым образом описать мироздание не получится.

Материя будет постоянно вносить помехи. Частично эти помехи тоже будут описываться математически, а именно в том случае, когда материя принимает в себя много структур разом. Но, скорее всего, мы будем сталкиваться с тем, что материя вносит просто белый шум, который отличается как раз отсутствием структуры, то есть является простым признаком бытия без всякого смысла.

Поэтому мне кажется, что помехи, вносимые материей, надо искать в каком-то другом месте. Этот вопрос пока остается открытым.

Соответствуют ли навыки счёта вашего ребенка его возрасту?

Полезно знать, какие цифры и навыки счета ребенок должен освоить к 3 — 4 годам. Просмотрите следующий список вех и отметьте, владеет ли этими знаниями ваш ребенок.

1. Знает — и ему любопытно — как числа и счет применимы к его жизни и окружающему миру.
2. Может правильно сосчитать не менее пяти предметов.
3. Может указывать на места в числовой строке и считать с соответствием 1 к 1 вдоль линии (слева направо, справа налево).
4. Понимает, что написанная цифра «3» означает три объекта — и то же самое с цифрами 1-5.
5. Может складывать и вычитать небольшое количество знакомых предметов. Например: «У меня три конфетки. А у тебя две. Сколько у нас вместе?»
6. Может ставить написанные цифры от 1 до 5 в правильном порядке, от меньшего до большего.
7. Можете считать от одного до десяти в правильном порядке.
8. Понимает понятия количества (например, «больше» и «меньше») и размера (например, «больше» и «меньше», «выше» и «ниже») и правильно использует эти термины.

Нуль — грандиозное открытие

Долгое время ученые считали, что ноль не существует. Казалось, что в математике непростительный пробел, который не может быть заполнен. Однако, когда ноль был введен в алгебру и геометрию, все изменилось. Это число стало своего рода магическим ключом в мире математики.

Нуль, вопреки своей назначению «ничто», имеет огромное значение. Он является отправной точкой для всех вычислений и операций. Без нуля нет возможности установить единичку, двойку или любое другое число. Он является фундаментом, на котором строится вся математическая система.

Если задуматься, ноль — это такое интересное число. Ноль и «ничто» кажутся синонимами, но они на самом деле не одно и то же. Ноль обладает математическим свойством, которое делает его неповторимым и уникальным.

Поэтому не стоит недооценивать маленькое и незаметное число — ноль. Ведь именно оно открыло нам новые возможности и позволило расширить границы математического знания.

Применение математики в повседневной жизни

Математика является одной из самых фундаментальных наук и оказывает огромное влияние на нашу повседневную жизнь. Ее применение можно наблюдать во многих областях, начиная от решения ежедневных задач и заканчивая профессиональной деятельностью.

Финансы: Математика играет важную роль в финансовом планировании. Она помогает в расчете процентов по кредитам, ипотеке, депозитам; определении стоимости акций и облигаций; прогнозировании доходности инвестиций и т.д. Без знаний математики невозможно правильно управлять своими финансами.

Торговля и экономика: В торговле и экономике математика неотъемлема. Она используется для анализа данных, прогнозирования спроса и предложения, определения оптимального ценообразования, оптимизации логистических цепочек и многое другое.

Транспорт и логистика: Математика является незаменимым инструментом в области транспорта и логистики. Она применяется для оптимизации маршрутов, планирования доставки, управления складскими запасами, расчета грузоподъемности и т.д.

Медицина и биология: В медицине и биологии математика используется для моделирования биологических систем, анализа медицинских данных, прогнозирования распространения болезней, разработки новых лекарств и т.д.

Архитектура и строительство: В архитектуре и строительстве математика применяется для расчета прочности конструкций, построении планов зданий и городов, определении необходимого количества материалов, разработке эстетических пропорций и т.д.

Это лишь некоторые из областей, где математика играет важную роль в повседневной жизни. При этом, даже в обыденных ситуациях, мы постоянно используем математические принципы и методы вроде расчета времени, денег, пространства и др.

Статьи по теме вопроса

• Основные понятия математики

  Математика является одной из наиболее важных и фундаментальных наук, которая изучает структуру, свойства и отношения между различными объектами. Она является неотъемлемой частью нашей жизни и применяется во многих областях, таких как физика, экономика, биология и технические науки….

• История развития математики

  Математика – это наука, которая изучает количество, структуру, пространство и изменения. Она является одной из самых древних наук и имеет богатую и интересную историю развития.Первые шаги в математикеПервые упоминания о математике можно найти уже в древнейшей письменности,…

• Роль математики в современном мире

  Математика – это наука, которая изучает структуру, свойства и взаимосвязи чисел, пространства, структур и изменений. Она является одной из самых фундаментальных наук и играет огромную роль в различных областях жизни.Математика в технологияхСовременный мир невозможно представить без…

• Математические методы и их применение

  Математика является одной из основных наук, которая широко используется в различных областях нашей жизни. Однако, ее значение не ограничивается только теоретическими вычислениями и формулами. Математические методы имеют большое практическое применение и помогают решать сложные задачи в…

• Математические теории и их значение

  Математика – это наука, которая изучает структуру, пространство, количество и изменение. Она является одной из самых фундаментальных наук и имеет широкое применение в различных областях жизни – от ежедневных расчетов до сложных научных исследований. В своей основе математика использует…

• Влияние математики на другие науки

  Математика – это одна из старейших и наиболее важных наук, которая играет огромную роль в развитии человечества. Ее применение не ограничивается только сферой точных наук, таких как физика или химия, но также оказывает значительное влияние на другие области знаний.Развитие…

• Задачи и проблемы, решаемые с помощью математики

  ВведениеМатематика – это наука о числах, формулах и пространстве. Она является одной из основных наук и играет важную роль в различных областях человеческой деятельности. Многие люди могут думать, что математика не имеет никакого отношения к их повседневной жизни, но на самом деле она…

• Современные достижения в области математики

  Математика является одной из старейших наук и постоянно развивается, открывая новые горизонты для исследований. Сегодня мы поговорим о самых значительных достижениях в области математики за последние несколько десятилетий.Искусственный интеллект и машинное обучениеОдним из…

• Интересные факты о математике

  Математика — это наука, которая изучает структуру, пространство, количество и изменение. Она играет важную роль в нашей жизни, от повседневных расчетов до сложных научных и технических разработок. Но помимо своей практической значимости, математика также представляет собой увлекательное поле…

• Практическое применение математики в повседневной жизни

  Математика является одним из фундаментальных наук, которая изучает структуру, свойства и взаимосвязь чисел, пространства, структур и изменений. Многие люди считают ее сложной и непонятной, однако она имеет огромное практическое применение в нашей повседневной жизни.ФинансыОдно из…

Математика, которая мне нравится

Пишите об интересных свойствах числа

. Картинки приветствуются!

Выкладываю свойства числа 10, которые прислал Лейб Александрович Штейнгарц.

1. У человека ДЕСЯТЬ пальцев на обеих руках. Именно это послужило причиной повсеместного распространения десятичной системы счисления.

2. ДЕСЯТЬ – это наименьшее многозначное число.

3. Эти два слова очень часто употребляются в математике. В каждом из них содержится ровно по 10 букв.

4. Число 10 является суммой первых четырех натуральных чисел:

5. Число 10 является суммой первых трех простых чисел:

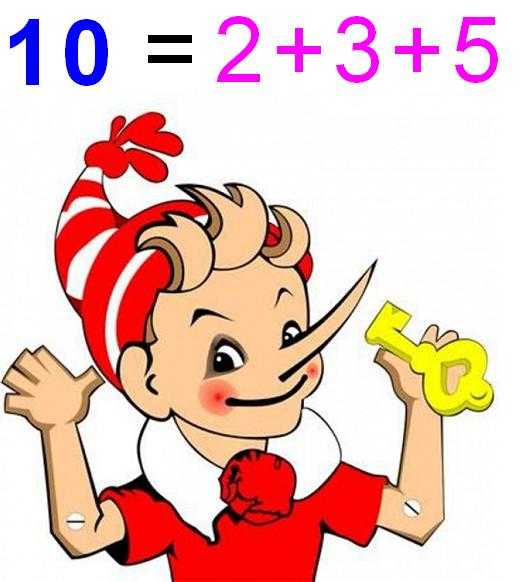
6. Число 10 является суммой первых четырех факториалов:

7. Самым простым признаком делимости является признак делимости на 10.

8. Наибольшее число на игральных картах – это число 10.

9. Любое действительное число можно представить в виде бесконечной ДЕСЯТИЧНОЙ дроби:

Эта запись представляет собой следующий ряд:

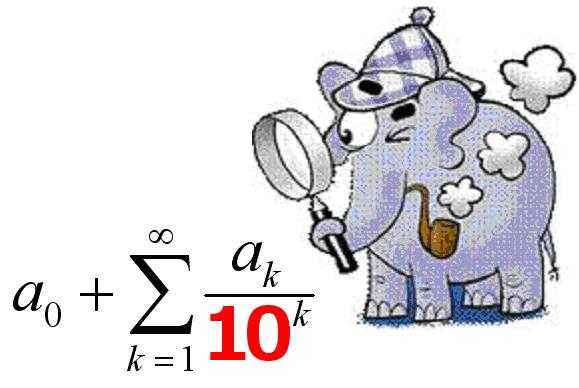
10. Всевышний дал ДЕСЯТЬ заповедей пророку Моисею на горе Синай.

11. В математике очень часто применяют ДЕСЯТИЧНЫЙ логарифм, основание которого обычно не пишется:

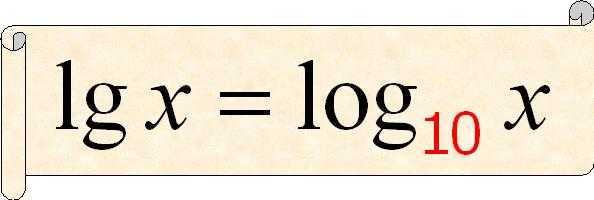
12. В международных (стоклеточных) шашках размер доски 10×10 клеток.

13. В слове ЧАЙКОВСКИЙ – 10 букв. Отец великого русского композитора был ДЕСЯТЫМ ребенком в семье За всю свою жизнь Петр Ильич Чайковский написал ровно ДЕСЯТЬ опер:

14. В слове МАТЕМАТИКА – 10 букв. В связи с этим, распутайте два арифметических ребуса.

Показать решение

15. Число 10 в двоичной системе счисления является числом 2 в десятичной системе счисления.

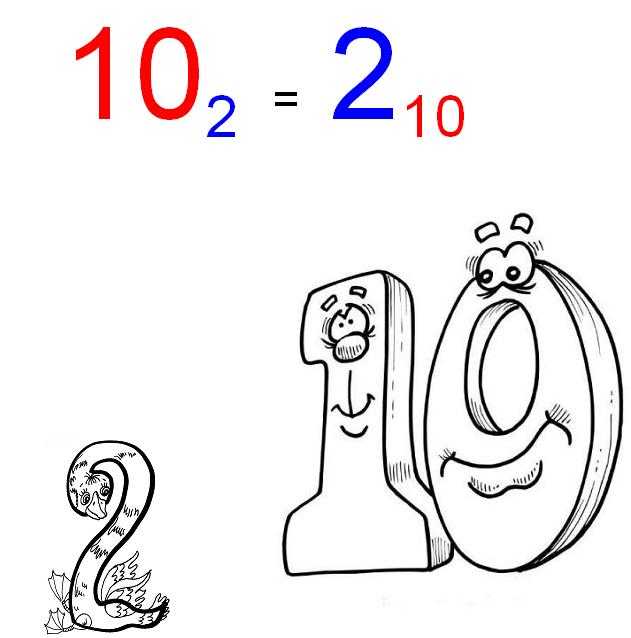
16. Популярна такая головоломка.

Показать решение

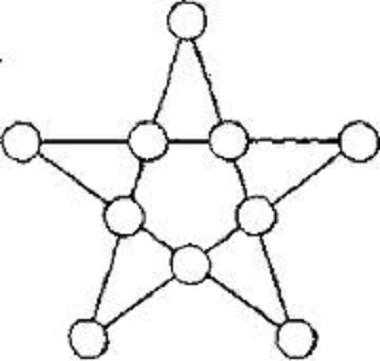
17. В слове АРИФМЕТИКА – 10 букв. В связи с этим, распутайте арифметический ребус.

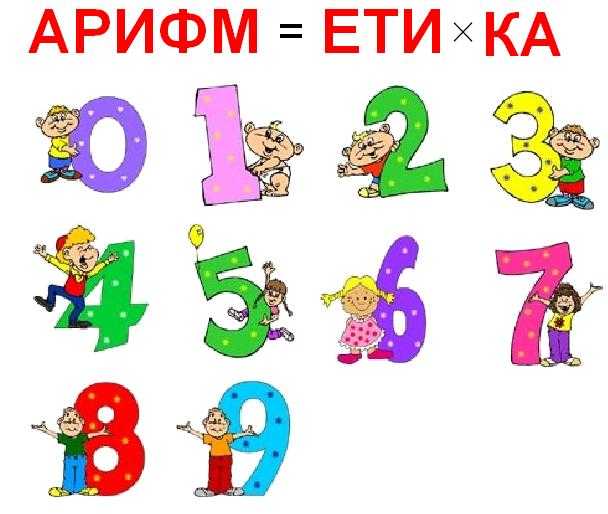
Показать решение

Имеется два способа:

18. ДЕСЯТОК:

• Счетная единица, равная десяти одинаковым предметам. Например, – ДЕСЯТОК ЯИЦ.

• Десять лет возраста. Например, – ЕМУ ПОШЕЛ СЕДЬМОЙ ДЕСЯТОК.

• НЕ РОБКОГО ДЕСЯТКА – о смелом человеке.

19. В фамилии МУСОРГСКИЙ – 10 букв. Очень известны ДЕСЯТЬ пьес для фортепиано (“Картинки с выставки”) великого русского композитора Модеста Мусоргского.

20. Червонец – денежная единица в Российской империи и СССР. Червонцами, начиная с начала XX века, традиционно называют банкноты номиналом в ДЕСЯТЬ единиц.

21. Прыжки в воду – один из водных видов спорта. Самая большая высота, с которой совершаются эти прыжки – 10 метров.

22. В фамилии МАТИЯСЕВИЧ 10 букв. Юрий Владимирович Матиясевич – российский математик, решивший знаменитую ДЕСЯТУЮ проблему Гильберта.

23. “Козлёнок, который считал до ДЕСЯТИ” — советский мультипликационный фильм. Главный герой мультфильма – Козлёнок, научившийся считать до десяти и стремящийся применить свое умение на практике.

24. В двух словах – ПЁТР ПЕРВЫЙ – содержится 10 букв.

Любопытно, что Пётр был провозглашён царём в1682 году (кстати, 8+2=10) в 10-летнем возрасте.

25. Числа Ферма – это числа вида (n – неотрицательное целое число):

Изучение чисел такого вида начал Ферма, который выдвинул гипотезу, что все они простые. Однако, эта гипотеза была опровергнута Эйлером, нашедшим разложение числа

на простые множители:

Любопытно, что в этом равенстве и слева, и справа расположено по ДЕСЯТЬ цифр.

26. КИЛОБАЙТ – единица измерения количества информации, равная 1024 байтам. То есть:

27. Попасть в ДЕСЯТКУ – • Делать что-либо очень точно. • Подбирать очень точные, меткие слова, рассказывая о чём-либо.

Посадка деревьев

Математические головоломки с ответами — самое то для детей.

На субботнике 2 класса ( 5В и 7А) сажали деревья по обе стороны парка. Пятиклассникам захотелось отличиться и, придя на час раньше второго класса, они посадили 5 деревьев. Но потом оказалось, что трудились они не на своей стороне и всю работу им пришлось начинать сначала.

7А управился, конечно, быстрее со своей, и пошел помогать другому классу. Выполнив всю работу, один шестиклассник заметил, что они ее перевыполнили. 5В на это ответил, что они, как и должны были, досадили свои 5 деревьев. Из-за этого завязался спор. Как вы думаете, кто прав?

Ответ: Шестиклассники перевыполнили свое задание, посадив на 10 деревьев больше, в отличие от 5В, который недовыполнил работу. Изначально ребята сажали не на своей территории, да и еще и в конце 5 за них досажали.

Математика развивает мышление

article>ÐаÑем занимаÑÑÑÑ ÑизкÑлÑÑÑÑой? ÐÑÐ²ÐµÑ Ð¿ÑоÑÑой â Ð´Ð»Ñ Ð·Ð´Ð¾ÑовÑÑ Ð¸ кÑаÑоÑÑ Ñела.

ÐаÑем ÑÑиÑÑ Ð¼Ð°ÑемаÑикÑ? ÐÑÐ²ÐµÑ Ð½Ð° ÑÑÐ¾Ñ Ð²Ð¾Ð¿ÑÐ¾Ñ ÐºÐ°Ð¶ÐµÑÑÑ Ð¼ÐµÐ½ÐµÐµ оÑевиднÑм.

ÐаÑемаÑика â ÑÑо гимнаÑÑика Ð´Ð»Ñ Ñма. ХоÑеÑÑ Ð½Ðµ ÑоÑеÑÑ, но в пÑоÑеÑÑе изÑÑÐµÐ½Ð¸Ñ Ð±ÑдÑÑ ÐºÑепÑаÑÑ ÐºÐ°ÑеÑÑва, коÑоÑÑе влиÑÑÑ Ð½Ð° ÑпоÑоб мÑÑлениÑ. ÐÐ»Ñ ÑÑого не обÑзаÑелÑно ÑÑиÑÑÑÑ Ð² пÑоÑилÑном клаÑÑе и ÑÑаÑÑвоваÑÑ Ð² Ð¾Ð»Ð¸Ð¼Ð¿Ð¸Ð°Ð´Ð°Ñ â ÑеÑение даже ÑамÑÑ Ð¿ÑоÑÑÑÑ Ð·Ð°Ð´Ð°Ñек на пÑопоÑÑии или Ñ Ð¿ÑоÑенÑами Ð´Ð°ÐµÑ Ð·Ð½Ð°ÑиÑелÑнÑй ÑÑÑекÑ.

ÐбобÑение, ÑокÑаÑение, анализ, ÑиÑÑемаÑизаÑиÑ, вÑделение важного, поиÑк закономеÑноÑÑей, ÑоÑмÑлиÑование гипоÑез и доказаÑелÑÑÑво ÑеоÑий â вÑе ÑÑо Ð¿Ð¾Ð¼Ð¾Ð³Ð°ÐµÑ ÑазвиÑÑ Ð¼ÑÑление, ÑделаÑÑ ÐµÐ³Ð¾ более гибким. ТоÑно Ñакже, как ÑизиÑеÑкие ÑпÑÐ°Ð¶Ð½ÐµÐ½Ð¸Ñ Ð´ÐµÐ»Ð°ÑÑ Ð½Ð°Ñе Ñело подвижнее, даÑÑ Ð·Ð°ÑÑд Ñил и ÑÑениÑÑÑÑ Ð²ÑноÑливоÑÑÑ, маÑемаÑика ÑÑениÑÑÐµÑ Ñм.

ÐаÑемаÑика ÑÐ°Ð·Ð²Ð¸Ð²Ð°ÐµÑ Ð¸Ð½ÑеллекÑ. ÐÐ°Ð±Ð¾Ñ Ð¿Ñавил и ÑÑнкÑий, коÑоÑÑе Ð¼Ñ Ð¸Ð·ÑÑаем в Ñколе, делаÑÑ Ð½Ð°Ñе мÑÑление поÑледоваÑелÑнÑм и логиÑнÑм. ЭÑо оÑÑажаеÑÑÑ Ð½Ð° Ñмении ÑаÑÑÑждаÑÑ, ÑоÑмÑлиÑоваÑÑ Ð¼ÑÑли и замеÑаÑÑ Ð²Ð·Ð°Ð¸Ð¼Ð¾ÑвÑзи. Ð Ñамое ÑвлекаÑелÑное, ÑÑо ÑÑи Ð·Ð½Ð°Ð½Ð¸Ñ Ð¼Ð¾Ð¶Ð½Ð¾ (и нÑжно!) пÑименÑÑÑ Ð½Ðµ ÑолÑко в Ñколе, но и в неÑÑандаÑÑнÑÑ ÑиÑÑаÑиÑÑ: ÑÑÐ¾Ð±Ñ Ð²ÑбÑаÑÑ ÑамÑÑ Ð²ÑгоднÑÑ Ð±Ð°Ð½ÐºÐ¾Ð²ÑкÑÑ ÐºÐ°ÑÑÑ, пÑоÑÑиÑаÑÑ Ð»Ð¸ÑÑÑ ÐºÑаÑки Ð´Ð»Ñ ÑемонÑа или ÑоздаÑÑ ÐºÐ°ÑÑÑ ÑокÑовиÑ, ÑÑÐ¾Ð±Ñ Ð½Ðµ забÑÑÑ Ð³Ð´Ðµ они ÑпÑÑÑанÑ.

ÐаÑемаÑика â ÑнивеÑÑалÑнÑй междÑнаÑоднÑй ÑзÑк, коÑоÑÑм владеÑÑ Ð¿Ð¾ÑÑи вÑе лÑди на земле. ЭÑи Ð·Ð½Ð°Ð½Ð¸Ñ Ð¿ÑигодÑÑÑÑ Ð² лÑбой ÑÑÑане и могÑÑ ÑÑаÑÑ Ð¿ÑедмеÑом инÑеÑеÑной беÑедÑ.

ÐайÑÑак!
ÐеобÑÑнÑй ÑпоÑоб познакомиÑÑÑÑ â ÑпÑоÑиÑÑ Ñеловека пÑо его оÑноÑение к маÑемаÑике, где он ее иÑполÑзÑÐµÑ Ð¸ Ð¿Ð¾Ð¼Ð½Ð¸Ñ Ð»Ð¸, как извлеÑÑ ÐºÐ²Ð°Ð´ÑаÑнÑй коÑÐµÐ½Ñ Ð¸Ð· ÑиÑла. Ðа, комÑ-Ñо ÑÑо покажеÑÑÑ ÑÑÑаннÑм, но заÑо Ð²Ð°Ñ ÑоÑно запомнÑÑ.

ЧÑо понÑÑÑ, заÑем ÑÑиÑÑ Ð¼Ð°ÑемаÑÐ¸ÐºÑ Ð² Ñколе, ÑолÑко пÑедÑÑавÑÑе, как пÑиÑÑно, когда в голове Ð½ÐµÑ Â«ÐºÐ°Ñи» и пÑÑаниÑÑ Ð² ÑаÑÑÑждениÑÑ. Ðа ÑÑÐ¾Ñ ÑÑÐµÑ ÐµÑе в пÑоÑлом веке великий ÑÑÑнÑй ÐомоноÑов Ñказал: «ÐаÑемаÑÐ¸ÐºÑ ÑолÑко заÑем ÑÑиÑÑ Ð½Ð°Ð´Ð¾, ÑÑо она Ñм в поÑÑдок пÑиводиÑ». Ðак ÑÑÑ Ð¼Ð¾Ð¶Ð½Ð¾ ÑпоÑиÑÑ?

ÐÑÑÑÑ Ð¾Ð±ÑÑÐµÐ½Ð¸Ñ Ð¼Ð°ÑемаÑике помогÑÑ Ð¿Ð¾Ð´ÑÑнÑÑÑ Ð¾Ñенки, подгоÑовиÑÑÑÑ Ðº конÑÑолÑнÑм, ÐÐР и Ñкзаменам.

Теория множеств и множественная логика: включение и операции над множествами

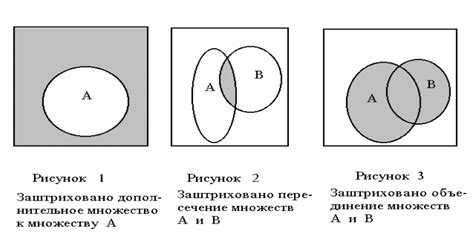
Теория множеств является одной из основных областей математики, изучающей свойства и отношения множеств. Множество — это совокупность объектов, которые образуют единое целое и называются его элементами. Основные операции над множествами включают объединение, пересечение, разность и дополнение.

Включение множеств

Одно множество может быть включено в другое, если все элементы первого множества также являются элементами второго множества. Математически это записывается как A ⊆ B, где A и B — множества. Если A включает все элементы B, но не является равным B, то говорят, что A является подмножеством B, обозначается как A ⊂ B.

Включение множеств используется для описания отношений между множествами и позволяет строить более сложные математические конструкции.

Операции над множествами

Операции над множествами позволяют комбинировать и преобразовывать множества, а также выражать различные отношения и свойства. Наиболее распространенные операции над множествами включают:

• Объединение (A ∪ B) — создает множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A и B.
• Пересечение (A ∩ B) — создает множество, состоящее из всех элементов, принадлежащих одновременно множествам A и B.
• Разность (A \ B или A — B) — создает множество, состоящее из всех элементов, принадлежащих множеству A, но не принадлежащих множеству B.
• Симметрическая разность (A Δ B) — создает множество, состоящее из всех элементов, принадлежащих множеству A или B, но не принадлежащих одновременно обоим множествам.

Эти операции позволяют строить более сложные множества и анализировать их свойства. Они часто используются в различных областях математики, логики, теории множеств, криптографии и т. д.

Изучение множественной логики и операций над множествами позволяет математикам решать сложные задачи, формулировать и доказывать теоремы, а также применять полученные знания в различных областях науки и техники.

Математические загадки на логику

Это очень полезная гимнастика для ума. Достаточно сложными являются логические математические загадки — с ответами на них придется немало подумать. Вот некоторые из них:

1. У Миши был большой, но кислый апельсин. А Витя ел большой, но сладкий. Что в апельсинах похоже, а что их отличает друг от друга? Схожи они тем, что оба большие, а различие в том, что один оказался вкусным, а второй — кислым.
2. Подружки Вера и Настя разглядывали иллюстрации. У одной из них в руках была книга, а у второй — журнал. Где разглядывала картинки Настя, если у Веры в руках был не журнал? Конечно же, в журнале.
3. Вася и Петя решили порисовать. Машину и трактор. Что было на картине у Васи, если Петя не хотел рисовать трактор? Конечно же, Вася рисовал машину.
4. Кристина, Витя и Слава жили в разноэтажных домах. Два из них были трехэтажными, один — двухэтажным. Кристина и Славик проживали не в одинаковых домах, Слава и Витя так же. Кто в каком доме жил? Эта задачка уже посложнее. Правильным будет ответ: Слава жил в двухэтажном доме, а Кристина и Витя — в трехэтажных.
5. Женя, Миша и Андрей любили заниматься чтением книг. Один интересовался машинами, другой — историями о войне, третий — о спорте. Кто о чем читал, если Женя не читал о войне и о спорте, а Миша не читал о спорте? Сложная на имеет достаточно простой ответ. Так как Женя не трогал книги про войну и спорт, значит, читал он о путешествиях. Миша не читал книгу о спорте, значит, он выбрал книгу о войне. Про Андрея информации нет, но методом исключения мы решаем, что ему достается книга о машинах. Все просто.
6. Вера, Маша и Олеся любили вышивать. Одна — сердечки, другая — домики, третья — узоры. Кто что вышивал, если Вера не вышивала сердечки и домики, а Маша не любила сердечки? Тоже довольно сложная задачка. Вера вышивала узоры, Маша — домики, Олеся — сердечки.

Что прочитать, чтобы вникнуть в основы математики?

Чтобы поднатореть в математике, нужно прочесть хотя бы какие-то вводные вещи, например, мою «Математику для гуманитариев» — книга есть в свободном доступе в интернете. За ней — «Что такое математика» Куранта и Роббинса. Можно читать Перельмана, но это, скорее, развлекаловка. Потом идет Иэн Стюарт «Величайшие математические задачи» — очень хорошая книга. Кто любит практику — «Кому нужна математика?» Райгородского. Под редакцией моего друга Николая Андреева вышла книга «Математическая составляющая», а недавно еще и новое издание — рекомендую. Уровень выше — математика для первого курса мехмата: «Введение в матанализ» Зорича, «Линейная алгебра и геометрия» Кострикина.

Так что умнейте. А дальше — уже вперед, на все этажи забирайтесь, господа альпинисты!

Прописи — раскраска

Набор развивающих карточек — прописей предназначены для развития графических навыков, моторной памяти, тренировки руки.

В комплекте 10 карточек и рисунками для раскрашивания . Эти прописи подойдут для тренировки руки дошкольников в детском саду и для первоклассников.

Для тренировки письма рекомендуется листы заламинировать и писать маркером на водной основе. Раскрашивать картинки тоже можно маркером, потом стирать влажной салфеткой. После тренировочного письма, можно предложить поработать цветными карандашами и ручкой.

Задания помогут развить мелкую моторику и координацию движений руки, формируют графические навыки и воображение ребёнка. Прописи помогут детям научится ориентироваться на листе бумаги в клеточку, задания разовьют зрительное восприятие, логическое мышление. Заниматься по настоящим прописям можно как индивидуально, так и в группе.

Для хранения карточек используется папка с кнопкой.

Номер 6: Компьютерная графика и математика

Многие люди думают, что для создания компьютерной графики не нужна математика. Но это далеко не так. Графика основана на математических принципах и алгоритмах, которые позволяют создавать линии, кривые, тени, освещение и многое другое.

• Пиксели и векторы. Каждый элемент графики состоит из множества пикселей – маленьких точек с определенным цветом. Для создания гладких линий и форм используются векторы – математические объекты, определяющие направление и длину линии.
• Матрицы трансформации. Для изменения размера и положения объекта на экране используются матрицы трансформации – математические объекты, представляющие движение, повороты и изменение масштаба объекта.
• 3D-графика. Для создания трехмерной графики используются математические объекты, такие как векторы и матрицы, чтобы определить положение объекта в трехмерном пространстве, его размеры, материалы и теневые эффекты.

Таким образом, математика позволяет создавать красивую и реалистичную компьютерную графику, которая выводит нашу жизнь на новый уровень.

Загадки математики: разгадать или сдаться?

1. Проблема П = NP.

Проблема P = NP является одной из великих загадок математики и информатики. Она заключается в определении отношения между двумя классами задач: P (Polynomial-time) и NP (Nondeterministic Polynomial-time). Суть вопроса заключается в том, можно ли эффективно решить задачу, проверяя предлагаемые решения с логической машиной в разумное время. Данная проблема является открытой и до сих пор не имеет окончательного решения.

2. Гипотеза P против NP.

Гипотеза P против NP является продолжением проблемы P = NP. Она заключается в утверждении, что P-задачи могут быть решены за полиномиальное время, в то время как NP-задачи требуют нелинейного времени. Однако, пока что не существует доказательства этой гипотезы, и она остается одной из самых сложных в математике.

3. Гипотеза Римана.

Гипотеза Римана — это одна из самых древних и сложных открытых проблем в математике. Она формулируется в терминах аналитической функции, называемой дзета-функцией Римана. Гипотеза утверждает, что все нетривиальные нули этой функции имеют вещественную часть, равную 1/2. Множество ученых и математиков пытались доказать или опровергнуть эту гипотезу, но до сих пор она остается нерешенной.

4. Задача о гильбертовых пространствах.

Задача о гильбертовых пространствах — это сложная математическая проблема, которая возникла из анализа геометрии в бесконечномерных пространствах. Она заключается в поиске наименьшего количества измерений, необходимого для представления набора данных или функции. Эта задача имеет множество приложений в физике, экономике и компьютерных науках, но до сих пор не имеет общего решения.

5. Задача о конечной проблеме конечности.

Задача о конечной проблеме конечности — это вопрос о том, существует ли алгоритм, который может определить, является ли определенный формальный язык бесконечным или конечным

Эта проблема имеет важное значение в теории формальных языков и автоматов. Несмотря на многочисленные исследования и попытки решить эту задачу, до сих пор не найдено общего алгоритма для ее решения