Однородные многочлены: определение и примеры

Одночлены и многочлены от одной переменной

      Одночленом (мономом) от переменной   x   называют   x ,  умноженную на число.

      , в которую возведена переменная   x,   называют степенью одночлена, а числовой множитель – коэффициентом одночлена.

      Если в одночлене степень переменной   x   не умножена ни на какое число, то считается, что коэффициент одночлена равен   1.

      Степень одночлена, являющегося числом, равняется нулю.

      Примеры одночленов от переменной   x:

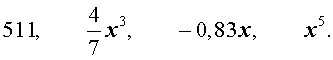
      Алгебраической суммой одночленов от переменной   x   называют один или несколько одночленов, соединенных между собой знаками сложения и вычитания. Аналогично определяется алгебраическая сумма чисел.

      Алгебраическую сумму одночленов от переменной   x   также называют многочленом или полиномом от переменной   x.   Например, многочленом является выражение

2×2 – 45x + 28×5 .

      Степенью многочлена называют наивысшую степень входящих в него одночленов.

      В частности, многочлен

ax + b ,

где буквами   a   и   b   обозначены произвольные числа, причем число   a    отлично от нуля, является многочленом первой степени.

      Многочлен

ax2 + bx + c ,

где буквами   a,   b   и   c   обозначены произвольные числа, причем число   a   отлично от нуля, является многочленом второй степени и называется квадратным трехчленом.

      Двучленом называется многочлен, состоящий из двух одночленов, трехчленом называется многочлен, состоящий из трех одночленов.

      Многочлен всегда можно расположить по возрастанию или по убыванию степеней входящих в него одночленов:

3 + 24x – 2×2 – x5 ;         – x5 – 2×2 + 24x + 3 .

      Число α называется корнем многочлена   p(x),   если

p(α) = 0.

      Например, квадратный трехчлен

x2 – 3x + 2

имеет два корня   x = 1   и   x = 2 .

Топ вопросов за вчера в категории Алгебра

Алгебра 10.11.2023 22:36 27 Смагулова Дильнара

Тіктөртбұрыштың периметрі 28см, ал диагонаоі 10 см. Тіктөртбұрыштың қабырғаларын теңдеулер жүйесін

Ответов: 2

Алгебра 09.12.2023 21:55 6 Азаров Даниил

Спростити вираз root(b * root(b, 5), 6) b > 0 Виберіть одну відповідь: root(b, 5) root(b ^ 3, 5)

Ответов: 1

Алгебра 20.06.2023 04:16 7 Соколова Ксюша

Изобразить на плоскости множество точек,заданных неравенством y-2x<-4

Ответов: 2

Алгебра 07.12.2023 23:48 13 Григорьев Сёма

3. Изобразите на плоскости множество точек, заданных неравенством y>3x-2​

Ответов: 2

Алгебра 02.07.2023 18:55 3 Давыдов Данил

Есть двузначное число, что в три раза больше десятков единиц. Умножение этого числа на сумму чисел

Ответов: 2

Алгебра 26.06.2020 07:14 33 Капачёва Ксения

Должно быть легко. Алгебра

Ответов: 1

Алгебра 23.09.2023 07:54 19 Луньков Никита

Літак виконав рейс з аеропорту А до аеропорту В за маршрутом довжиною 1800 км зі швидкістю х

Ответов: 2

Алгебра 06.05.2023 13:14 45 Саломатин Паха

Какое число нужно возвести в квадрат чтобы получить 5?

Ответов: 3

Алгебра 04.05.2019 19:27 12 Кукуруза Влад

Помогите.25 БАЛЛОВ ЗА ЛЕГКОЕ ЗАДАНИЕ»!!!! Из семи бегунов и трех прыгунов нужно составить команду

Ответов: 2

Алгебра 04.07.2023 10:51 19 Бодещенко Андрей

Объясните подробно,когда в графике функции ставится круглая скобка,а когда квадратная. ПРОШУ ПОМОЧЬ​

Ответов: 2

Степень многочлена – как ее найти?

Еще одним важным сопутствующим определением является определение степени многочлена. Сначала определим степень многочлена стандартного вида, это определение базируется на степенях одночленов , находящихся в его составе.

Определение.

Степень многочлена стандартного вида
– это наибольшая из степеней входящих в его запись одночленов.

Приведем примеры. Степень многочлена 5·x 3 −4
равна 3
, так как входящие в его состав одночлены 5·x 3
и −4
имеют степени 3
и 0
соответственно, наибольшее из этих чисел есть 3
, оно и является степенью многочлена по определению. А степень многочлена 4·x 2 ·y 3 −5·x 4 ·y+6·x
равна наибольшему из чисел 2+3=5
, 4+1=5
и 1
, то есть, 5
.

Теперь выясним, как найти степень многочлена произвольного вида.

Определение.

Степенью многочлена произвольного вида
называют степень соответствующего ему многочлена стандартного вида.

Итак, если многочлен записан не в стандартном виде, и требуется найти его степень, то нужно привести исходный многочлен к стандартному виду, и найти степень полученного многочлена – она и будет искомой. Рассмотрим решение примера.

Пример.

Найдите степень многочлена 3·a 12 −2·a·b·c·a·c·b+y 2 ·z 2 −2·a 12 −a 12
.

Решение.

Сначала нужно представить многочлен в стандартном виде:3·a 12 −2·a·b·c·a·c·b+y 2 ·z 2 −2·a 12 −a 12 =

=(3·a 12 −2·a 12 −a 12)−
2·(a·a)·(b·b)·(c·c)+y 2 ·z 2 =

=−2·a 2 ·b 2 ·c 2 +y 2 ·z 2
.

В полученный многочлен стандартного вида входят два одночлена −2·a 2 ·b 2 ·c 2
и y 2 ·z 2
. Найдем их степени: 2+2+2=6
и 2+2=4
. Очевидно, наибольшая из этих степеней равна 6
, она по определению является степенью многочлена стандартного вида −2·a 2 ·b 2 ·c 2 +y 2 ·z 2
, а значит, и степенью исходного многочлена.
, 3·x
и 7
многочлена 2·x−0,5·x·y+3·x+7
.

Список литературы.

• Алгебра:
  учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Мордкович А. Г.
  Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 17-е изд., доп. — М.: Мнемозина, 2013. — 175 с.: ил. ISBN 978-5-346-02432-3.
• Алгебра
  и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / ; под ред. А. Б. Жижченко. — 3-е изд. — М.: Просвещение, 2010.- 368 с. : ил. — ISBN 978-5-09-022771-1.
• Гусев В. А., Мордкович А. Г.
  Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Или, строго, — конечная формальная сумма вида

∑
I
c
I
x
1
i
1
x
2
i
2
⋯
x
n
i
n
{\displaystyle \sum _{I}c_{I}x_{1}^{i_{1}}x_{2}^{i_{2}}\cdots x_{n}^{i_{n}}}

В частности, многочлен от одной переменной есть конечная формальная сумма вида

c
0
+
c
1
x
1
+
⋯
+
c
m
x
m
{\displaystyle c_{0}+c_{1}x^{1}+\dots +c_{m}x^{m}}

С помощью многочлена выводятся понятия «алгебраическое уравнение » и «алгебраическая функция ».

О числе однородных невырожденных p-ичных функций заданной степени

Пусть p простое число, F = GF(p), Vn n-мерное векторное пространство над F, е базис пространства Vn. Пусть также р: Vn ^ F. Функция р называется e-однородной, если р(х) = nv,e(x) для всех х G Vn, где nv,e однородный многочлен от n переменных над F, имеющий степень не более p 1 по каждой переменной, а x набор координат вектора х в базисе е. Функция р называется невырожденной, если deg р ^ 1 и deg dvр = (deg р) 1 для любого v G Vn \ {0}, где (dvр)(х) = р(х + v) р(х) для всех v,x G Vn. Получена формула для числа HNp(n, d) е-однородных невырожденных функций р: Vn ^ F, имеющих степень d (это число не зависит от е), а именно: если n ^ 1 и d G {1,…,n(p 1)}, n k p то HNp(n,d) = Е (-1)fcp(2)+{«dfe}p n = Е (-1)|S|pCT(S)-|S|+{n dS|}p, где k=0 SC{1…..n} n биномиальk m \ обобщённый биномиальный коэффициент порядка p dp p ный коэффициент Гаусса; ct(S) сумма всех элементов множества S. Доказано, что HNp(n, d) ^ p{d}p 1 (pn 1) (p{ d }p 1 J /(p 1) для любых d ^ 1 и jnj n ^ d/(p-1). Используя…

Универсальное обобщение алгоритма цепной дроби

Простое обобщение. Пусть в трехмерном вещественном пространстве заданы три вещественные однородные линейные формы. Их модули дают отображение этого пространства в другое. В нем рассматривается выпуклая оболочка образов всех целочисленных точек первого пространства, кроме его начала координат. Замыкание этой выпуклой оболочки названо модульным многогранником. Наилучшие целочисленные приближенияккорневымподпространствам заданныхформдаютточки,образы которыхлежатнаграницемодульногомногогранника.Границамодульного многогранника вычисляется любой стандартной программой вычисления выпуклых оболочек. Алгоритм дает также периодичность для кубическихиррациональностей сположительным дискриминантом. Обобщить цепную дробь пытались Эйлер, Якоби, Дирихле, Эрмит, Пуанкаре, Гурвиц, Клейн, Минковский, Вороной и многие другие. Универсальное обобщение. Пусть в n-мерном вещественном пространстве R n заданы l линейных и k квадратичных форм (n = l +2k). Модули этих форм задают отображение пространства R n …

Умножение одночлена на многочлен

Напомним распределительный закон умножения:

Используя этот закон, можно производить умножение одночлена на многочлен.

Пример. Перемножьте выражения 5v2 и 9v3 + 2t4.

Решение: Запишем произведение выражений:

Такое раскрытие скобок можно объяснить с помощью «метода фонтанчика»:

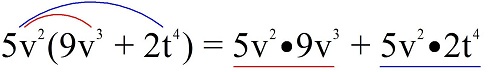
От множителя 5v2 строят линии (синего цвета к) КАЖДОМУ слагаемому в скобке. Каждой такой линии соответствует отдельное произведение в получаемом полиноме.

После раскрытия скобок получили два произведения одночлена на одночлен, которые считаем по отдельности (см. урок 3):

Можно сформулировать следующее правило умножения многочлена на одночлен:

Ещё один пример. Перемножьте полином 2x2y + 4xy2 – 1 и моном – 3ху.

Решение:

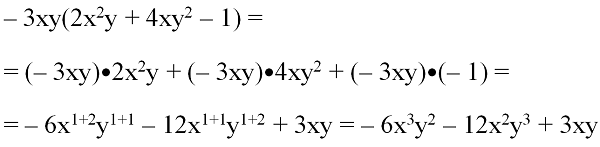
Здесь метод «фонтанчика» будет выглядеть так:

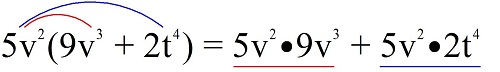
Можно заметить, что после умножения монома на полином получится столько одночленов, сколько их было в исходном полиноме. Это правило можно использовать для самоконтроля.

Однородный и неоднородный

Период, термин однородный прилагательное, указывающее на то, что оно одинаково для различных элементов, составляющих определенную группу или набор, в свою очередь, термин неоднородный Это прилагательное, обозначающее, что что-то состоит из различных частей.

В области химии эти два термина используются для определения соединений. Смесь может быть однородной или неоднородной.

В однородная смесь Это тот компонент, компоненты которого нельзя различить невооруженным глазом, они образованы растворенным веществом и растворителем, например: водой (растворителем), смешанной с сахаром (растворенным веществом).

В гетерогенная смесь Это та смесь, в которой ее компоненты могут быть легко дифференцированы и разделены, такие как вода и масло, оба соединения могут быть легко обнаружены и разделены методом декантации.

Что такое однородное:

Однородный — прилагательное, обозначающее относительно одного пола, обладающих одинаковыми персонажами.

Слово однородный имеет древнегреческое происхождение. гомогены состоит из гомо что означает «такой же» и генос выражая «класс».

Однородный термин состоит из элементов с общими характеристиками, связанными с их классом или природой, что позволяет установить между ними отношения равенства и единообразия.

Слово однородный может использоваться в разных контекстах.

В социальные науки, социальная однородность относится к обществу, в котором все его члены равны, говорят на одном языке и разделяют одни и те же убеждения и обычаи, что снижает вероятность социальных конфликтов, таких как: религиозные, языковые и другие.

Также в область статистики, термин однородный относится к стратификации, при которой существует немногочисленное разнообразие.

Слово «однородный» может использоваться как синоним для слов «подобный», «подобный», «подобный», «однородный» и т. Д. Некоторые антонимы термина однородный: разнородные, разные.

Однородная система

А однородная система В области химии он состоит из одной фазы, это означает, что интенсивные свойства имеют одинаковую ценность во всех своих точках.

Точно так же гомогенная система представляет собой смесь нескольких веществ однородного состава, то есть различные вещества или части, образующие ее, не могут быть различимы как сахар, растворенный в воде.

Гомогенная система делится на: растворы, она имеет единственную видимую фазу, и они образованы растворителем и растворенным веществом, путем дистилляции или кристаллизации они могут быть разделены на другие компоненты, и чистые вещества — это те вещества, которые невозможно получить. другие вещества или компоненты с помощью методов фракционирования.

Однако на научном уровне однородный баланс относится ко всем реакциям, в которых элементы находятся в одной фазе, то есть в том же химическом состоянии, что и смесь газов или жидкий раствор.

См. Также Раствор и растворитель.

Одночлены и многочлены от нескольких переменных

      Одночленом (мономом) от переменных   x₁ ,  x₂ , … , x_n   называют выражение вида:

где   c   – произвольное число, называемое коэффициентом одночлена, а символами

i₁ ,  i₂ , … i_n

обозначены целые неотрицательные числа.

      Таким образом, одночлен от нескольких переменных является произведением числа на несколько букв, каждая из которых входит в одночлен .

      Степенью одночлена называют сумму степеней всех входящих в него букв, т.е. сумму целых неотрицательных чисел:

i₁ +  i₂ + … + i_n .

      Число   c   называют коэффициентом одночлена.

      Пример. Степень одночлена

равна   3,   а коэффициент равен   – 0,83 .

      Два одночлена равны, если, во-первых, у них равны коэффициенты, а во-вторых, одночлены состоят из одних и тех же букв, которые входят в них с соответственно равными показателями степеней.

      Алгебраическая сумма одночленов от нескольких переменных носит название многочлена или полинома от нескольких переменных. Например,

      Степенью многочлена от нескольких переменных называют наивысшую степень входящих в него одночленов.

      В частности, степень многочлена

равна   8.

      Многочлен от нескольких переменных называют однородным многочленом, если степени всех входящих в него одночленов равны. В этом случае степень многочлена равна степени каждого входящего в него одночлена.

      Например, многочлен

является однородным многочленом степени   3.

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Определение многочлена

article>ÐногоÑлен â ÑÑо ÑÑмма одноÑленов. ÐолÑÑаеÑÑÑ, ÑÑо многоÑлен â не ÑÑо иное, как неÑколÑко одноÑленов, ÑобÑаннÑÑ Â«Ð¿Ð¾Ð´ одной кÑÑÑей».

ÐдноÑлен â ÑÑо пÑоизведение, ÑоÑÑоÑÑее из ÑиÑлового множиÑÐµÐ»Ñ Ð¸ одной или неÑколÑÐºÐ¸Ñ Ð¿ÐµÑеменнÑÑ, ÐºÐ°Ð¶Ð´Ð°Ñ Ð¸Ð· коÑоÑÑÑ Ð²Ð·ÑÑа в неоÑÑиÑаÑелÑной ÑÑепени.

РаÑÑмоÑÑим пÑимеÑÑ Ð¼Ð½Ð¾Ð³Ð¾Ñленов:

• 15x + 7x
• 4ab â b + 3

ÐÑли многоÑлен ÑоÑÑÐ¾Ð¸Ñ Ð¸Ð· двÑÑ Ð¾Ð´Ð½Ð¾Ñленов, его назÑваÑÑ Ð´Ð²ÑÑленом:

• 10x â 3×2
• 10x â одноÑлен
• â3×2 â одноÑлен

ÐногоÑлен â ÑÑо ÑÑмма одноÑленов, поÑÑÐ¾Ð¼Ñ Ð·Ð½Ð°Ðº «минÑÑ» оÑноÑиÑÑÑ Ðº ÑиÑÐ»Ð¾Ð²Ð¾Ð¼Ñ ÐºÐ¾ÑÑÑиÑиенÑÑ Ð¾Ð´Ð½Ð¾Ñлена. Ðменно поÑÑÐ¾Ð¼Ñ Ð¼Ñ Ð·Ð°Ð¿Ð¸ÑÑваем â3×2, а не пÑоÑÑо 3×2.

ЭÑÐ¾Ñ Ð¶Ðµ многоÑлен можно запиÑаÑÑ Ð²Ð¾Ñ Ñак:

10x â 3×2 = 10x â 3×2 = 10x + (â3×2).

ЭÑо знаÑиÑ, ÑÑо каждÑй одноÑлен важно ÑаÑÑмаÑÑиваÑÑ Ð²Ð¼ÐµÑÑе Ñо знаком, коÑоÑÑй пеÑед ним ÑÑоиÑ.

ÐногоÑлен вида 10x â 3×2 + 7 назÑваеÑÑÑ ÑÑеÑÑленом.

ÐинейнÑй двÑÑлен â ÑÑо многоÑлен пеÑвой ÑÑепени: ax + b. a и b здеÑÑ â некоÑоÑÑе ÑиÑла, x â пеÑеменнаÑ.

ÐÑли ÑазделиÑÑ Ð¼Ð½Ð¾Ð³Ð¾Ñлен Ñ Ð¿ÐµÑеменной x на линейнÑй двÑÑлен x â b (где b â некоÑоÑое положиÑелÑное или оÑÑиÑаÑелÑное ÑиÑло) â оÑÑаÑок бÑÐ´ÐµÑ ÑолÑко многоÑленом нÑлевой ÑÑепени. То еÑÑÑ Ð½ÐµÐºÐ¾ÑоÑÑм ÑиÑлом N, коÑоÑое можно опÑеделиÑÑ Ð±ÐµÐ· поиÑка ÑаÑÑного.

ÐÑли многоÑлен ÑодеÑÐ¶Ð¸Ñ Ð¾Ð±ÑÑное ÑиÑло â ÑÑо ÑиÑло ÑвлÑеÑÑÑ ÑвободнÑм Ñленом многоÑлена.

ÐапÑимеÑ, в многоÑлене 6a + 2b â x + 2 ÑиÑло 2 â ÑвободнÑй Ñлен.

СвободнÑй Ñлен многоÑлена не Ð¸Ð¼ÐµÐµÑ Ð±Ñквенной ÑаÑÑи. ÐÑоме Ñого, лÑбое ÑиÑловое вÑÑажение â ÑÑо многоÑлен. ÐапÑимеÑ, Ð²Ð¾Ñ Ñакие ÑиÑловÑе вÑÑÐ°Ð¶ÐµÐ½Ð¸Ñ â Ñоже многоÑленÑ:

• 16 + 13
• (7 â 2) â 9
• (25 + 25) : 5

Такие вÑÑÐ°Ð¶ÐµÐ½Ð¸Ñ ÑоÑÑоÑÑ Ð¸Ð· ÑвободнÑÑ Ñленов.

Связанные определения [ | ]

• Многочлен вида
  c
  x
  1
  i
  1
  x
  2
  i
  2
  ⋯
  x
  n
  i
  n
  {\displaystyle cx_{1}^{i_{1}}x_{2}^{i_{2}}\cdots x_{n}^{i_{n}}}
  называется одночленом
  или мономом
  мультииндекса
  I
  =
  (i
  1
  ,
  …
  ,
  i
  n)
  {\displaystyle I=(i_{1},\dots ,\,i_{n})}
  .
• Одночлен, соответствующий мультииндексу
  I
  =
  (0
  ,
  …
  ,
  0)
  {\displaystyle I=(0,\dots ,\,0)}
  называется свободным членом
  .
• Полной степенью
  (ненулевого) одночлена
  c
  I
  x
  1
  i
  1
  x
  2
  i
  2
  ⋯
  x
  n
  i
  n
  {\displaystyle c_{I}x_{1}^{i_{1}}x_{2}^{i_{2}}\cdots x_{n}^{i_{n}}}
  называется целое число
  |
  I
  |
  =
  i
  1
  +
  i
  2
  +
  ⋯
  +
  i
  n
  {\displaystyle |I|=i_{1}+i_{2}+\dots +i_{n}}
  .

• Множество мультииндексов I
  , для которых коэффициенты
  c
  I
  {\displaystyle c_{I}}

  ненулевые, называется носителем многочлена
  , а его выпуклая оболочка — многогранником Ньютона
  .

• Степенью многочлена
  называется максимальная из степеней его одночленов. Степень тождественного нуля доопределяется значением
  −
  ∞
  {\displaystyle -\infty }
  .
• Многочлен, являющийся суммой двух мономов, называется двучленом
  или биномом
  ,
• Многочлен, являющийся суммой трёх мономов, называется трёхчленом
  .

• Коэффициенты многочлена обычно берутся из определённого коммутативного кольца
  R
  {\displaystyle R}

  (чаще всего поля , например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом
  R
  {\displaystyle R}

  без делителей нуля) которое обозначается
  R

  .
  {\displaystyle R.}

• Для многочлена
  p
  (x)
  {\displaystyle p(x)}
  одной переменной, решение уравнения
  p
  (x)
  =
  0
  {\displaystyle p(x)=0}
  называется его корнем .

Полиномиальные функции

Пусть
A
{\displaystyle A}

есть алгебра над кольцом
R
{\displaystyle R}

.
Произвольный многочлен
p
(x)
∈
R

{\displaystyle p(x)\in R}
определяет полиномиальную функцию

p
R:
A
→
A
{\displaystyle p_{R}:A\to A}

Чаще всего рассматривают случай
A
=
R
{\displaystyle A=R}
.

В случае, если
R
{\displaystyle R}

есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов), функция
f
p:
R
n
→
R
{\displaystyle f_{p}:R^{n}\to R}
полностью определяет многочлен p.
Однако в общем случае это неверно, например: многочлены
p
1
(x)
≡
x
{\displaystyle p_{1}(x)\equiv x}
и
p
2
(x)
≡
x
2
{\displaystyle p_{2}(x)\equiv x^{2}}
из
Z
2

{\displaystyle \mathbb {Z} _{2}}
определяют тождественно равные функции
Z
2
→
Z
2
{\displaystyle \mathbb {Z} _{2}\to \mathbb {Z} _{2}}
.

Полиномиальная функция одного действительного переменного называется целой рациональной функцией .

Степень многочлена

Многочлен может иметь степень — имеет на это полное право.

Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.

Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.

1. Приводим многочлен к стандартному виду.
2. Выбираем одночлен с наибольшей степенью.

Рассмотрим на примере:

Дан многочлен 6x + 4xy2 + x + xy2

Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:

• 6x и x — подобные слагаемые
• 4xy2 и xy2 — подобные слагаемые

Получаем многочлен стандартного вида 6x + 4xy2 + x + xy2 = 7x + 5xy2.

• Степень первого одночлена (7x) — 1.
• Степень второго одночлена (5xy2) — 3.
• Наибольшая из двух степеней — 3.

Отсюда делаем вывод, что многочлен 7x + 5xy2 — многочлен третьей степени.

Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy2 + x + xy2 — многочлен третьей степени, поскольку оба многочлена равны друг другу.

В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.

Пример:

Дан многочлен 6xx2 + 5xx2 − 3xx3 − 3x2x

Приведем его к стандартному виду: 6xx3 + 5xx2 − 3xx3 − 3x2x = 6×4 + 5×3 − 3×4 − 3×3

Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:

• 5×3 и −3×3 — подобные слагаемые.
• 6×4 и −3×4 — подобные слагаемые.
• 6×4 + 3×3 − 3×4 − 3×3 = 3×4 − 2×3
• 6xx3 + 5xx2 − 3xx3 − 3x2x — многочлен четвертой степени.

Однородный многочлен

Однородные многочлены от х и у ( то есть такие многочлены, у которых все члены имеют одинаковую степень) и рациональные дроби, имеющие такие члены, преобразуются введением кратных дуг, что понижает степень.
 

Однородный многочлен ( квадратичная форма), определяемый формулой ( 3), называется положительно определенным, если он принимает лишь неотрицательные значения и обращается в нуль, лишь когда все & равны нулю. Аксиома 4 требует, следовательно, чтобы квадратичная форма ( 3) была положительно определенной.
 

Однородный многочлен / равен нулю в 2п общих точках кривых К и S. Выбирая подходящим образом координаты, мы можем исключить случай, когда t оо является одной из точек пересечения S с К.
 

Однородный многочлен Р из леммы 1 является гармонической функцией.
 

Однородный многочлен Р веса л определяется своими значениями на л-мерных декартовых произведениях проективных пространств.
 

Однородный многочлен / степени г по переменным а есть линейная комбинация таких одночленов.
 

Однородный многочлен второй степени ( квадратичная форма) будет знаке / определенным, если он сохраняет постоянный знак при вещественных значениях аргументов, обращаясь в пуль только при обращении в нуль всех аргументов. Если же этот многочлен, сохраняя знак, может обращаться в нуль при значениях аргументов, не равных одновременно нулю, то он называется знакопостоянным.
 

Это однородный многочлен, степень которого равна длине кода; ои очень напоминает тэта-ряд решетки ( см. формулы ( 31) и ( 32) гл.
 

Полагая однородный многочлен и степени / от х, у, г равным r Yt, мы замечаем, что У, зависит только от координат 0, ф и является функцией положения на единичной сфере.
 

Пространство гармонических однородных многочленов степени п линейно. Это пространство, очевидно, инвариантно относительно поворотов.
 

Назовем однородным многочленом или формой степени га многочлен h ( X. Хп), все члены которого имеют одну и ту же полную степень га. Формы степеней 1, 2, 3 называются соответственно линейной, квадратичной и кубичной формами.
 

Нт — однородный многочлен ( форма) степени т относительно координат и импульсов. Аддитивная постоянная ( равная значению функции Гамильтона в положении равновесия) не влияет на уравнения движения и в разложении ( 44) отброшена.
 

Число членов однородного многочлена ( 1) равно С, при этом считаются и те члены многочлена, у которых коэффициент равен нулю.
 

Это свойство однородных многочленов может служить основанием для очень полезного расширения понятия однородности функции.
 

Рз являются однородными многочленами степеней 30, 20 и 12 соответственно. Нули многочлена рз в проективном пространстве, состоящем из всех прямых, проходящих через начало координат в С2, образуют двенадцать вершин правильного икосаэдра, нули многочлена р2 образуют средние точки двадцати граней этого икосаэдра, а нули многочлена р образуют средние точки тридцати ребер этого икосаэдра.
 

Умножение многочлена на многочлен

Пусть нам надо перемножить два полинома, a+bи c+d. Запишем их произведение:

Заменим выражение a + b переменной k:

Теперь исходное произведение можно выразить как произведение монома и полинома:

Проведем обратное преобразование, заменив k на a + b:

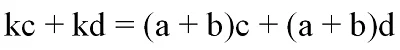
Наконец, раскроем скобки в этом выражении:

Эту формулу можно проиллюстрировать геометрически. Рассмотрим прямоугольник со сторонами a + b и c + d:

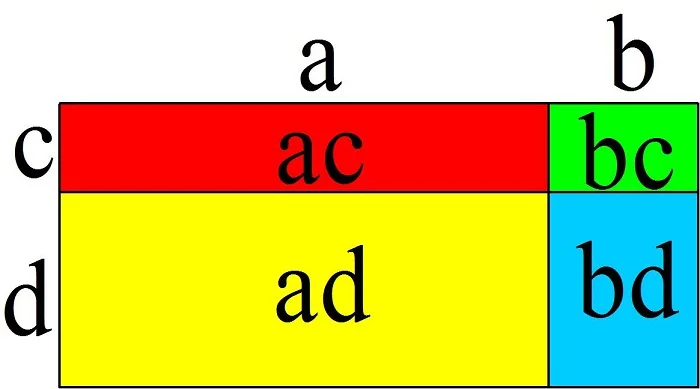
Площадь этого прямоугольника, как и любого другого, равна произведению его сторон, то есть(a + b)(c + d).С другой стороны, она состоит из 4 прямоугольников, чьи площади также вычисляются как произведения их сторон, и составляют ac, bc, ad и bd. Поэтому можно записать равенство

Получается, что для умножения многочлена на многочлен нужно перемножать попарно все мономы, входящие в их состав, после чего сложить их.

Если в одном полиноме содержится m слагаемых, а в другом n, то результатом их перемножения окажется новый полином, содержащий m•n мономов (до приведения подобных слагаемых). Для перемножения многочленов также используется метод «фонтанчика».

Пример. Найдем произведение выражений 3a2 – 4ab + b2и 2a– b.

Решение: В первом полиноме содержится 3 монома, а во втором – 2, поэтому после их перемножения мы получим сумму 3•2 = 6 одночленов:

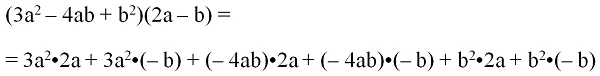
Раскрытие скобок «фонтанчиком» будет выглядеть так:

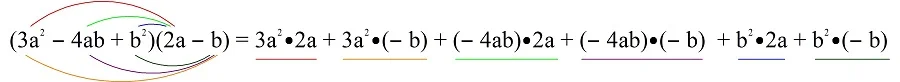
В результате действительно получилась сумма 6 мономов. Осталось вычислить каждый из них, после чего привести подобные слагаемые:

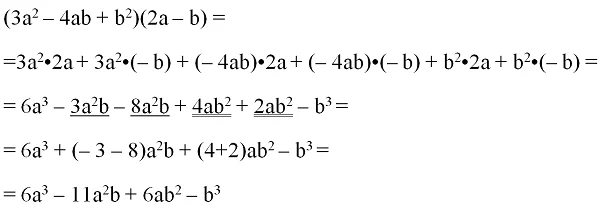
Заметим, что при перемножении полиномов происходит сложение степеней многочленов. Действительно, в рассмотренном выше примере мы умножили полином второй степени 3a2 – 4ab + b2 на полином первой степени 2a– b, и получили в результате многочлен 3-ей (2+1) степени.

Также возможно умножение многочленов в столбик. Особенно это удобно делать в случае с полиномами с одной переменной.

Пример. Найдите произведение выражений 2×3 + 3×2 +5x + 9 и x2 + 4x + 7.

Решение: Запишем полиномы в столбик, один под другим:

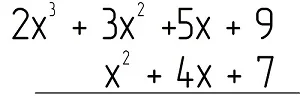
Далее умножим самый правый моном второго многочлена, то есть число 7, на первый полином, и запишем его ниже:

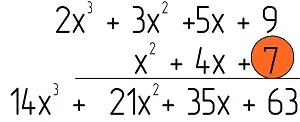
Далее умножим следующий моном, 4х, на первый полином, и запишем результат ещё ниже, причем сместим запись чуть влево, чтобы подобные члены оказались друг под другом:

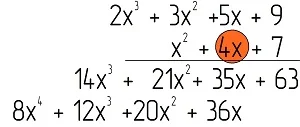
Также умножим последний одночлен, x2, на первый полином:

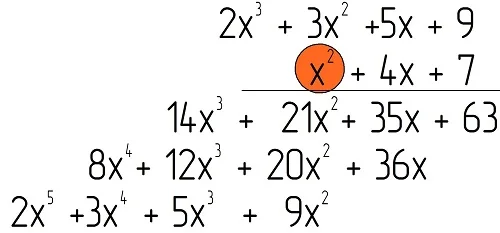
Осталось сложить подобные слагаемые (то есть переменные х с одинаковыми степенями), которые записаны друг под другом:

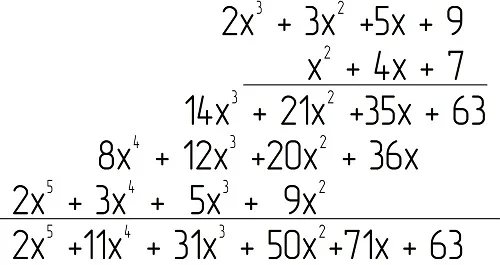
Ещё раз цветом выделим подобные слагаемые и результаты их суммирования:

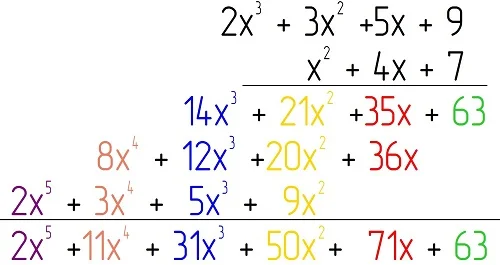
Ответ: 2х5 + 11х4 + 31х3 + 50х2 + 71х +63.

Многочлен и его члены – определения и примеры

В 7 классе многочлены изучаются сразу после одночленов, это и понятно, так как определение многочлена
дается через одночлены. Дадим это определение, объясняющее что такое многочлен.

Определение.

Многочлен
– это сумма одночленов; одночлен считается частным случаем многочлена.

Записанное определение позволяет привести сколько угодно примеров многочленов. Любой из одночленов 5
, 0
, −1
, x
, 5·a·b 3
, x 2 ·0,6·x·(−2)·y 12
, и т.п. является многочленом. Также по определению 1+x
, a 2 +b 2
и — это многочлены.

Для удобства описания многочленов вводится определение члена многочлена.

Определение.

Члены многочлена
– это составляющие многочлен одночлены.

Например, многочлен 3·x 4 −2·x·y+3−y 3
состоит из четырех членов: 3·x 4
, −2·x·y
, 3
и −y 3
. Одночлен считается многочленом, состоящим из одного члена.

Определение.

Многочлены, которые состоят из двух и трех членов, имеют специальные названия – двучлен
и трехчлен
соответственно.

Так x+y
– это двучлен, а 2·x 3 ·q−q·x·x+7·b
– трехчлен.

В школе наиболее часто приходится работать с линейным двучленом
a·x+b
, где a
и b
– некоторые числа, а x
– переменная, а также с квадратным трехчленом
a·x 2 +b·x+c
, где a
, b
и c
– некоторые числа, а x
– переменная. Вот примеры линейных двучленов: x+1
, x·7,2−4
, а вот примеры квадратных трехчленов: x 2 +3·x−5
и .

Многочлены в своей записи могут иметь подобные слагаемые . Например, в многочлене 1+5·x−3+y+2·x
подобными слагаемыми являются 1
и −3
, а также 5·x
и 2·x
. Они имеют свое особое название – подобные члены многочлена.

Определение.

Подобными членами многочлена
называются подобные слагаемые в многочлене.

В предыдущем примере 1
и −3
, как и пара 5·x
и 2·x
, являются подобными членами многочлена. В многочленах, имеющих подобные члены, можно для упрощения их вида выполнять приведение подобных членов .

Изучение и применение [ | ]

Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры».

С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля , отрицательных , а затем и комплексных чисел , а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.

Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (см. аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе .

Многочлены также играют ключевую роль в алгебраической геометрии , объектом которой являются множества, определённые как решения систем многочленов.

Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре , теории узлов и других разделах математики для кодирования или выражения многочленами свойств различных объектов.