Термины, используемые для ориентации
Как только оси и плоскости, которые пересекаются и разделяют тело в анатомическом положении, известны, можно установить отношения между ними и различными анатомическими структурами.
Кроме того, можно определить относительные отношения между структурами и плоскостями в соответствии с положением тела, если оно отличается от анатомического положения. Это очень полезно при выполнении хирургических доступов.
Термины, используемые для описания расположения анатомических элементов в соответствии с плоскостями и осями, следующие:
— Головной.
— Поток.
— Проксимальный.
— Дистальный.
— Вентральный.
— Спинной.
— Медиальный.
— Боковая сторона.
Чтобы определить местонахождение любой анатомической структуры, необходимо указать как минимум две из ранее упомянутых характеристик, а также точку отсчета. Если это не указано, то одна из описанных ранее осей и плоскостей считается универсальной точкой отсчета.
Ось в технической механике:
Ось — это элемент конструкции, представляющий собой деталь соосного соединения двух или более частей механизма. Оси используются для передачи силы, вращения и поддержания точного положения различных деталей механизма.
Оси могут быть изготовлены из различных материалов, таких как сталь, алюминий, чугун и т. д. Они обычно имеют цилиндрическую форму и могут быть полыми или заполненными. Оси могут быть одиночными или соединены вместе с помощью втулок или других элементов.
Оси играют важную роль в работе механизмов. Они обеспечивают жесткую связь между двумя или более деталями, позволяют им вращаться относительно друг друга и переносить механическую нагрузку. Оси также позволяют точно выставить нужное положение деталей и предотвратить их смещение.
Применение осей в технической механике очень обширно. Они используются в различных отраслях промышленности, таких как машиностроение, автомобилестроение, судостроение и т. д. Оси находят применение как в крупных механизмах, так и в мелких инструментах и бытовой технике.
Одним из примеров применения оси является вращение колес на автомобиле. Колеса устанавливаются на оси, которые в свою очередь крепятся к подвеске автомобиля. Оси позволяют колесам свободно вращаться и переносить груз автомобиля.
Еще одним примером применения осей является механизм часов. Внутри механизма находятся различные оси, которые позволяют стрелкам двигаться и указывать время. Оси в часах обеспечивают точное положение стрелок и их вращение.
В заключение, оси представляют собой важный элемент в технической механике и широко используются в различных механизмах. Они обеспечивают передачу силы и вращения, а также поддерживают точное положение деталей. Без осей многие механизмы не смогли бы работать эффективно.
Примеры осей в геометрии
Ось симметрии
Осью симметрии называется прямая, вокруг которой выполняется симметричное отображение фигуры. Например, у круга или равнобедренного треугольника с основанием, параллельным оси ординат, будет существовать ось симметрии.
Ось вращения
Осью вращения называется прямая, вокруг которой выполняется поворот фигуры. Например, у цилиндра осью вращения является прямая, параллельная оси ординат и проходящая через его основания.
Оси симметрии многогранников
У многих многогранников, таких как куб, правильный тетраэдр или октаэдр, существует несколько осей симметрии. Например, у куба всего 9 осей симметрии – 3 оси, параллельные осям координат, и 6 осей, проходящих через середины противоположных граней.
Симметрали
Симметралями называются прямые, перпендикулярные основной оси симметрии, которые разделяют фигуру на две равные части. Например, у прямоугольника с основаниями, параллельными осям координат, симметралями будут серединные перпендикуляры к его сторонам.
Примеры осей в геометрии
Фигура
Тип оси
Круг
Ось симметрии
Равнобедренный треугольник
Ось симметрии
Цилиндр
Ось вращения
Куб
Ось симметрии
Прямоугольник
Симметрали
Примеры использования поперечного направления
Существует ли простой способ, чтобы запомнить разницу между поперечным и продольным направлением?
Да, есть простой способ запомнить разницу между поперечным и продольным направлением. Представьте себе, что вы находитесь на перекрестке и переходите дорогу, двигаясь поперек пути движения транспорта. Это поперечное направление. А теперь представьте, что вы идете по длинной улице, двигаясь вперед, вдоль улицы. Это продольное направление.
Поперечное направление играет важную роль во многих сферах нашей жизни. Вот несколько примеров, где знание поперечного направления может быть очень полезным:
1. Дорожное движение: Запомните, что поперечно направление соответствует пешеходному переходу, а продольно — движению автомобилей. Поперечное направление будет также указывать на перпендикулярность между дорогой и прилегающими улицами. Выучите эти правила и сдать экзамен по ПДД будет намного проще!
Как запомнить разницу между поперечным и продольным направлением?
Простой способ запомнить разницу между поперечным и продольным направлением — это представить себе поперечный проход в перекрестке, а продольный — прямую дорогу, вдоль которой можно двигаться.
2. Работа с деревом или металлами: Поперечное направление часто используется для обозначения сечения дерева или металла. Например, при работе с деревом поперечное направление указывает на направление, перпендикулярное росту дерева, а продольное — вдоль роста.
3. Медицина: Поперечное направление может использоваться для описания местоположения органов тела. Например, поперечное сечение живота будет перпендикулярно продольной плоскости тела.
4. Работа с картами и компасами: При использовании компаса или чтении карты, поперечное направление поможет вам определить коротчайший путь или разницу между двумя точками. Следуйте поперечному направлению и не заблудитесь!
5. Изучение основ: При изучении новой темы или конспектировании уроков, поперечное направление может помочь вам облегчить запоминание информации. Используйте стишки-запоминалки или создайте схемы и рисунки, чтобы лучше запомнить содержание.
Важно понимать разницу между поперечным и продольным направлением и уметь применять эту информацию в нужных ситуациях. Сравните различия и запомните, что поперечное направление пересекает другие направления, а продольное направление соответствует идущему вперед. Не забывайте об этом при решении задач и подготовке к экзаменам!
Не забывайте об этом при решении задач и подготовке к экзаменам!
Оси в геометрических фигурах
Ось геометрической фигуры – это линия или прямая, которая делит фигуру на две симметричные части. Она является основой для изучения симметрии и других характеристик фигур. Оси используются не только в плоской геометрии, но и в трехмерных пространствах.
В зависимости от формы и типа фигуры, оси могут быть различными. Вот несколько примеров:
- Ось симметрии – это линия, которая делит фигуру на две равные и симметричные части. Например, равнобедренный треугольник имеет ось симметрии, проходящую через вершину и середину основания.
- Ось вращения – это линия, вокруг которой фигура может вращаться без изменения своей формы. Круг, например, имеет бесконечное количество осей вращения.
- Ось отражения – это линия, через которую фигура отражается без изменения формы. Примером служит ось отражения зеркала.
- Ось симметрии и вращения – некоторые фигуры имеют одновременно оси симметрии и вращения. Примером является квадрат, у которого четыре оси симметрии и четыре оси вращения.
Оси в геометрических фигурах помогают нам понять их свойства и взаимодействие с другими фигурами. Они также играют важную роль в решении различных задач и заданий в математике и физике.
Выбрать другой язык:
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
- Добавить термин
График гиперболы
Опять же вспоминаем тривиальную «школьную» гиперболу .
Выполним чертеж:
Основные свойства функции :
Область определения: .
Область значений: .
Запись обозначает: «любое действительное число, исключая ноль»
В точке функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись обозначает, что мы бесконечно близко приближаемся по оси к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись обозначает, что мы бесконечно близко приближаемся по оси к нулю справа. При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .
Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.
В данном случае ось является вертикальной асимптотой для графика гиперболы при .
Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.
Также односторонние пределы , говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.
Исследуем функцию на бесконечности: , то есть, если мы начнем уходить по оси влево (или вправо) на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .
Таким образом, ось является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.
Функция является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .
График функции вида () представляет собой две ветви гиперболы.
Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).
Если , то гипербола расположена во второй и четвертой координатных четвертях.
Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.
Пример 3
Построить правую ветвь гиперболы
Используем поточечный метод построения, при этом, значения выгодно подбирать так, чтобы делилось нацело:
Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.
Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.
Координационные оси здания
Здание, или какое либо сооружение в плане разделяется условными осевыми линиями на ряд сегментов. Данные линии определяющие положение основных несущих конструкций, называются продольными и поперечными координационными осями.
Интервал между координационными осями в плане здания называют шагом, а по преобладающему направлению шаг может быть продольным или поперечным.
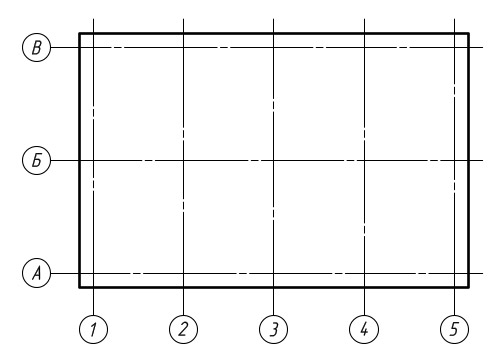
Маркировка координационных осей
В том случае если расстояние, между координационными продольными осями, совпадает с пролётом, перекрытием или покрытием, основной несущей конструкции, то этот интервал называют пролетом.

Высота этажа в многоэтажном жилом доме
За высоту этажа Нэт принимается расстояние от уровня пола выбранного этажа до уровня пола вышерасположенного этажа. По тому же принципу определяют и высоту верхнего этажа, при чём толщину перекрытия чердака принимают условно равной толщине междуэтажного перекрытия с. В промышленных одноэтажных строениях высота этажа равна расстоянию от пола до нижней поверхности конструкции покрытия.
С целью определения взаимного расположения частей здания используют сетку координационных осей, определяющую несущие конструкции данного строения.
Координационные оси наносятся штрих пунктирными тонкими линиями и маркируются внутри окружностей диаметром от 6 до 12 мм .
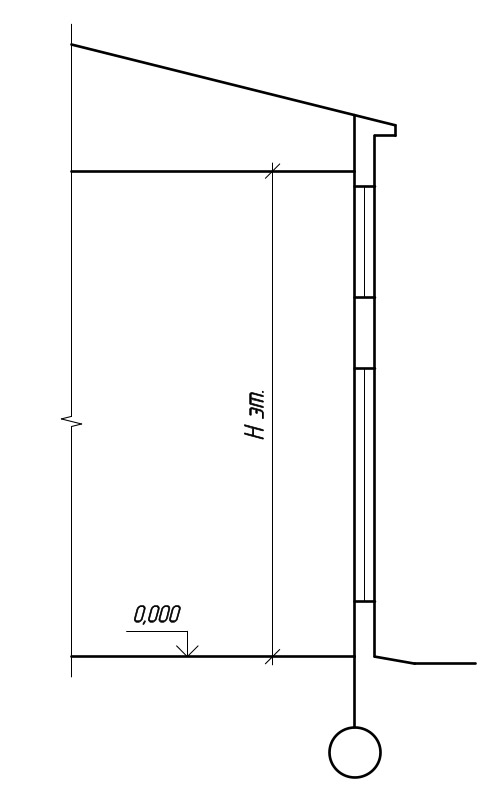
Высота этажа в одноэтажном здании
Маркировка координационных осей производится арабскими цифрами и прописными буквами, за исключением символов: 3 , Й , О , X , Ы , Ъ , Ь .
Высота шрифта обозначающего координационные оси выбирается на один-два номера больше, чем величина чисел на этом же листе.
Цифрами обозначают оси по стороне здания с наибольшим количеством координационных осей.
Направление маркировки осей наносят с лева на право, по горизонтали и снизу вверх, по вертикали.
Маркировка осей располагается, как правило, по левой и нижней сторонам плана здания.
Координационную ось наружной стены располагают на расстоянии, а = 100 мм, соблюдая отступ для установки плит перекрытия.

Координационные оси наружных и внутренних стен
Источник
Что такое продольная ось?

Функция продольной оси заключается в определении и ориентации объекта в пространстве. Она помогает определить положение объекта относительно окружающих его элементов и обеспечивает соответствующую ориентацию и симметрию объекта.
Примеры объектов, имеющих продольную ось, включают автомобили, самолеты, корабли и здания. Продольная ось в автомобилях и самолетах проходит от передней части до задней части, что позволяет им двигаться в прямом направлении. В кораблях продольная ось направлена от носа к корме, обеспечивая их движение вперед и назад. В зданиях продольная ось проходит от одной стороны до другой, задавая главное направление здания.
Важные уточнения по процедуре измерения углов установки колес
Предлагаемый метод дает возможность только определять углы установки колес (УУК), чтобы получить представление о текущих параметрах схода и развала. Дальнейшие работы по их регулировке можно проводить как своими руками (при наличии соответствующего опыта и знаний), так и в автомастерских.
Подразумевается, что замеры проводятся при исправной подвеске и нормальном давлении в шинах. Поэтому соответствующие работы, связанные с диагностикой и ремонтом ходовой части, не рассматриваются.
Также необходимо учесть, что в данной статье не рассматривается, какими должны быть углы схода и развала. Речь пойдет только о процессе их измерений. Полученные результаты в дальнейшем нужно сравнить с заводскими значениями, которые могут отличаться для автомобилей разных марок и моделей.
Перед замерами углов схода и развала необходимо разместить автомобиль на ровной твердой поверхности – например, на бетонном полу гаража. Заезжая на рабочую площадку, следует держать руль в нулевом положении. При этом колеса будут стоять максимально близко к тому положению, в котором они находятся при движении авто по прямой дороге.
Если же автомобиль после остановки будет подниматься на домкрате или подъемнике, это приведет к разгрузке подвески, затем колеса станут на пол недостаточно ровно. Для устранения таких погрешностей понадобятся поворотные круги или сдвижные платформы, которых большинство автовладельцев не имеют. Поэтому приподнимать кузов перед проведением замеров настоятельно не рекомендуется. Подвеска машины должна быть под привычной нагрузкой.
Начинать замеры следует с определения углов схода, поскольку именно эти параметры регулируются на большинстве моделей автомобилей. Данная характеристика определяется для каждого из четырех колес, поэтому ее иногда называют «полусхождением». Индивидуальный сход замеряют относительно продольной оси автомобиля. Ее можно построить несколькими способами, рассмотрим подробнее.
Продольное и поперечное в строительстве: основные отличия и приоритеты
Продольное направление применяется для описания объектов, чьи размеры изменяются вдоль главной оси. Например, длина комнаты — это продольный размер, поскольку он измеряется вдоль стены. Продольное направление также связано с основным направлением движения или расположения объекта.
С другой стороны, поперечное направление применяется для определения размеров, перпендикулярных главной оси объекта. Например, ширина комнаты — это поперечный размер, поскольку он измеряется от одной стены до другой, перпендикулярно продольному направлению. Поперечное направление обычно перпендикулярно к продольному.
Основные отличия между продольным и поперечным направлениями проявляются в разных аспектах строительства.
Строительные материалы: При выборе материалов для строительства обращают внимание на их способность выдерживать нагрузки в продольном и поперечном направлениях. Некоторые материалы могут быть более подходящими для продольных конструкций, таких как стены, тогда как другие материалы лучше подходят для поперечных элементов, таких как перекрытия или покрытия
Прочность и устойчивость: Продольные элементы обычно имеют более высокую прочность, так как они должны выдерживать тяжелые нагрузки, например, от веса стен или крыши
Поперечные элементы, в свою очередь, могут быть менее прочными, но играют важную роль в обеспечении устойчивости всей конструкции. Например, столбы и балки могут использоваться для поддержки поперечных элементов.
Функциональность и эффективность: Продольное и поперечное направления могут оказывать влияние на функциональность и эффективность использования объекта. Например, расположение перегородок в продольном направлении может определять различные функциональные зоны, а поперечные проемы и двери могут обеспечивать удобный доступ к этим зонам.
При проектировании и строительстве необходимо учитывать как продольные, так и поперечные аспекты. Тщательный анализ и планирование помогут оптимизировать использование пространства и обеспечить долговечность и функциональность построенного объекта.
Применение оси в различных отраслях промышленности
Ось, как конструктивный элемент, широко применяется в различных отраслях промышленности и играет важную роль в многих работах. В данном разделе рассмотрим несколько примеров использования оси в разных сферах деятельности.
Машиностроение и автомобильная промышленность:
- В машиностроении оси используются в различных механизмах и машинах для передачи момента силы и обеспечения вращения. Они применяются, например, в двигателях, трансмиссиях и приводах.
- В автомобильной промышленности оси играют важную роль в системе подвески, обеспечивая стабильность и маневренность автомобиля.
Судостроение:
В судостроении оси применяются для передачи силы от двигателей к винтам и рулевым устройствам судна. Они обеспечивают движение и маневренность судна.
Энергетика:
В энергетике оси используются в различных механизмах и оборудовании: в турбинах, генераторах, насосах и других устройствах, где необходимо передавать вращение.
Горнодобывающая промышленность:
В горнодобывающей промышленности оси применяются в шахтных лебедках для подъема и опускания грузов.
Производство и строительство:
- В производстве оси используются в различных станках и механизмах для обеспечения вращения и передачи силы.
- В строительстве оси применяются в строительных машинах и оборудовании: кранах, буровых установках, подъемниках, гидравлических системах и т.д.
Это лишь несколько примеров применения оси в различных отраслях промышленности. Она является неотъемлемой частью многих механизмов и оборудования, обеспечивая надежную и эффективную работу.
Связь графика функции и первообразной
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?

Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
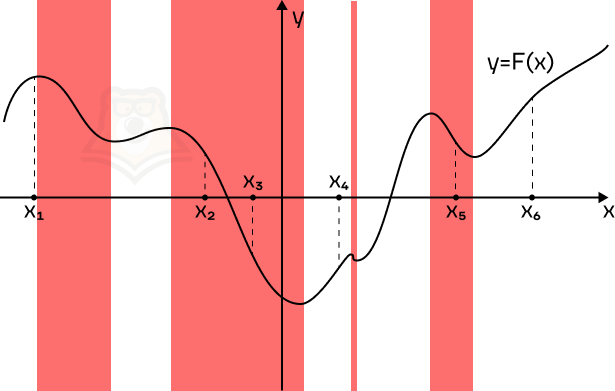
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке .

Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
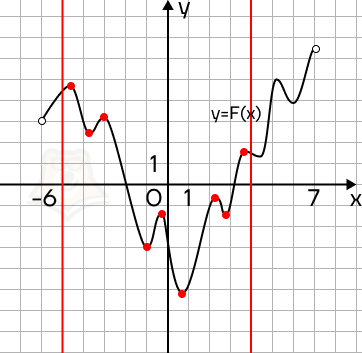
Ответ: 9
| Чем кофе похож на функцию, ее первообразную и производную? Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток. Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная. Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной. |

2.3. Привязка стен к координационным осям
На
чертежах зданий роль координатной сетки
играют координационные оси капитальных
стен. После нанесения на план координационных
осей выполняют привязку
к ним конструктивных элементов , в первую
очередь, наружных и внутренних несущих
стен и опор. Привязка осуществляется
простановкой размеров от оси до обеих
граней стены или колонны. При этом ось
стены не проводят на всём её протяжении,
а продляют лишь на величину, необходимую
для простановки размера привязки. Оси
опорных колонн принято чертить двумя
взаимно перпендикулярными отрезками
штрихпунктирных линий.
Координационные
оси не всегда совпадают с геометрическими
осями стен. Их положение задаётся с
учётом размеров стандартных пролётных
конструкций балок, ферм и плит перекрытия.
В примере на рис. 8 для наглядности
частично показана раскладка панелей
перекрытия и их опирание на стены. Панели
вычерчены прямоугольниками с тонкими
диагоналями.
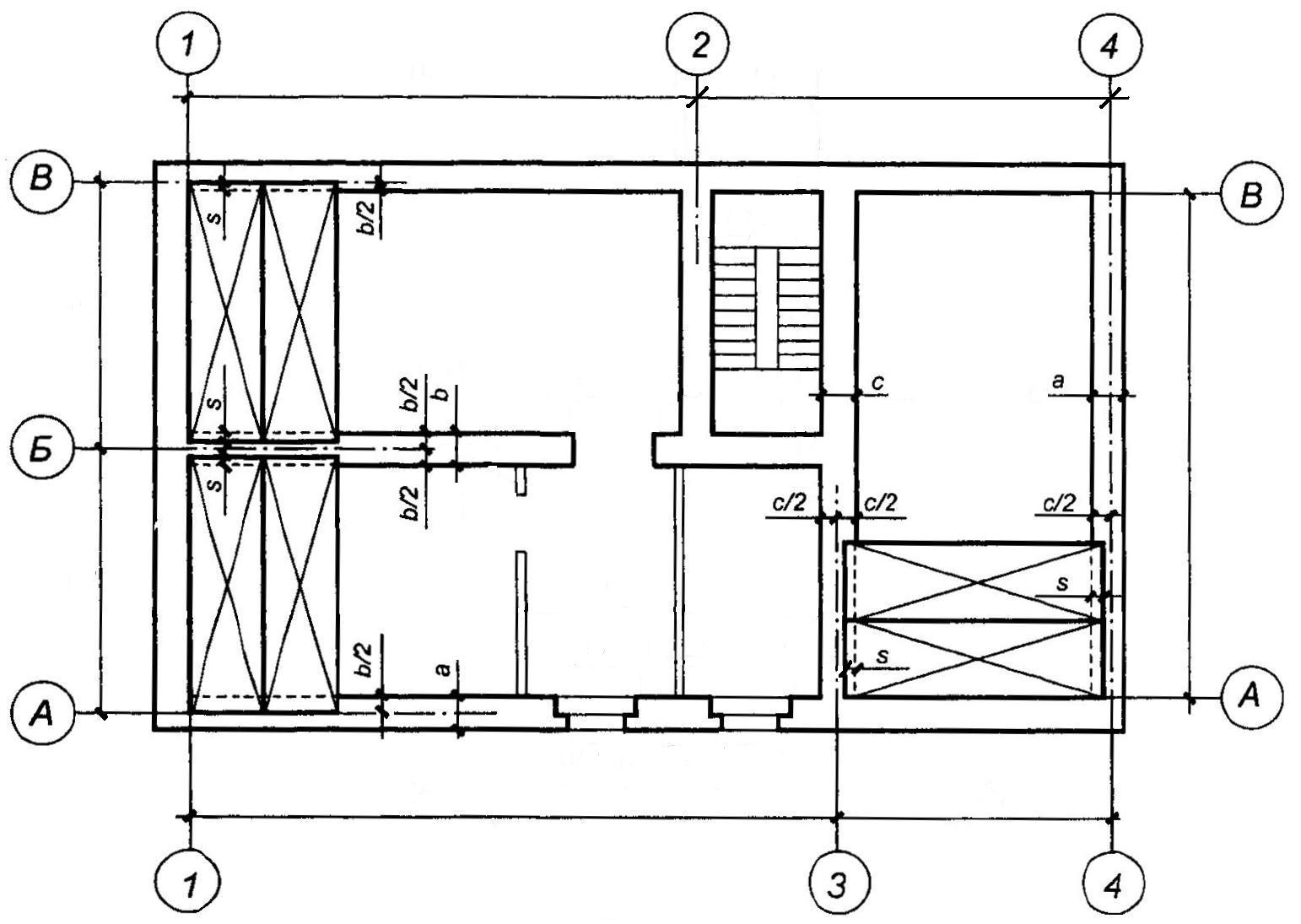
Рис.8.
Привязки
капитальных стен на плане здания
Привязку
стен к модульным координационным осям
в зданиях с несущими продольными или
поперечными стенами осуществляют,
исходя из следующих указаний:
на
внутренних
стенах
их геометрическая
ось, как правило,
со-
вмещается
с координационной осью (рис. 9, а
;
рис. 8, ось Б, ось 3);
допускается
не совмещать геометрическую и
координационную
оси
стен лестничных клеток , стен с
вентиляционными каналами и т.п.;
в
стенах лестничных клеток оси проводятся
на расстоянии, кратном модулю, от
внутренней (обращённой в сторону
лестницы) грани стены (рис. 9,б
;
рис. 8, ось
2
);
в
наружных несущих стенах координационная
ось проводится от
а)
б) в)
г)
Рис.9.
Варианты
привязок несущих стен
внутренней
(обращённой в сторону помещения) грани
стены на расстоянии, равном половине
толщины соответствующей внутренней
несущей стены (рис. 9,в
;
рис. 8, ось
А
,
ось
В
,
ось
4
);
в
наружных самонесущих стенах выполняется
так называемая
нулевая
привязка –
координационная ось совмещается с
внутренней
гранью
стены – (рис. 9,г
;
рис. 8, ось
1
);
если
наружная стена является на разных
своих участках несу-
щей
(участок
стены по оси А между осями 1 и 3
)
и самонесущей (участок
стены по оси А между осями 3 и 4
),
то координационная ось ориентируется
по несущему участку (рис.8);
привязка
колонн и стен производственных зданий
зависит от их
положения
в одном из рядов (средних, крайних или
торцевых); варианты таких привязок
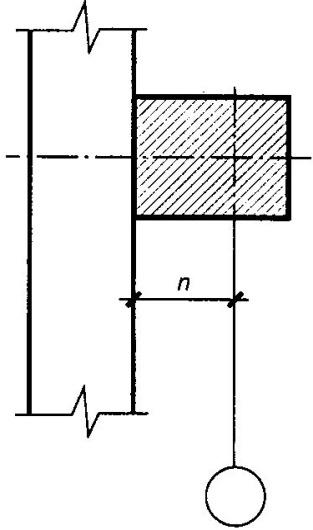
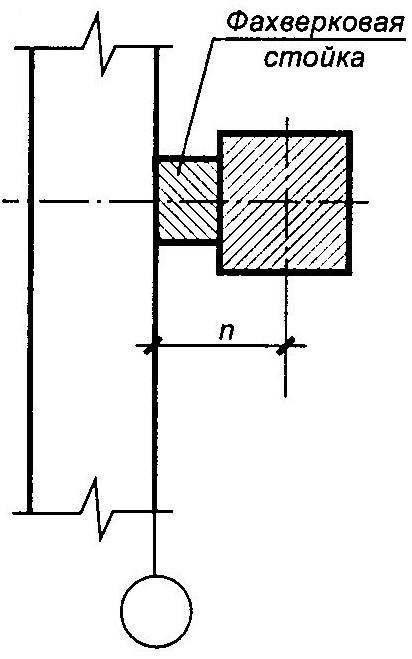
показаны на рис. 10.
 а)
а)
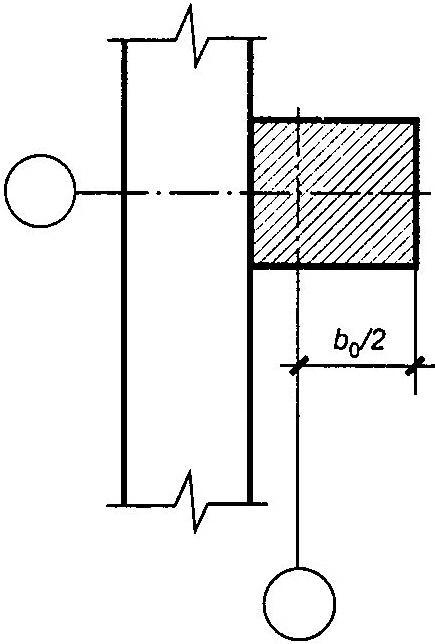 б)
б)
в)
 г)
г)
 д)
д)
 е)
е)
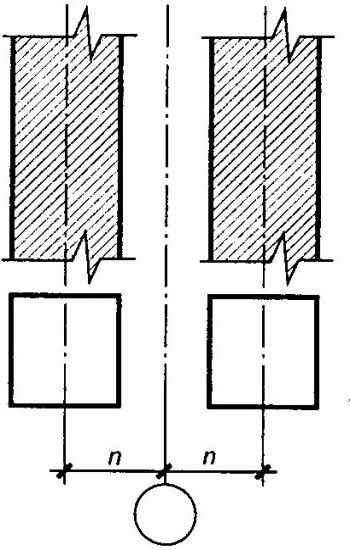
 ж)
ж)
 з)
з)
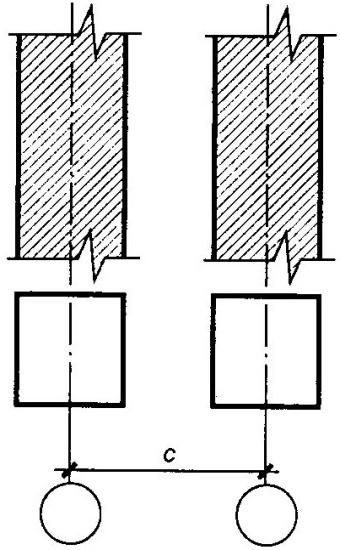
и)
Рис.10.
Привязки
колонн к координационным осям:
Заключение
Способы измерения УУК автомобиля, рассмотренные в данной статье, практически не используются на профессиональных автосервисах. Компьютерный метод более удобен и эффективен, требует меньших затрат времени. Но в быту автомобилистов часто бывают ситуации, когда визит на СТО затруднен по разным причинам: например, если машина временно не на ходу, не хватает финансов, или когда водителю нужно лишь убедиться в нормальном состоянии подвески машины. В таких ситуациях предложенная технология оптимально подойдет для замера углов схода/развала и станет достойной альтернативой компьютерной диагностике УУК.




























