Определение неравенств: основные понятия
Неравенство — это математическое выражение, утверждающее, что одна величина меньше, больше или не равна другой. В отличие от равенства, неравенство позволяет сравнивать значения и устанавливать отношение между ними.
В неравенстве используются следующие математические символы:
- > — знак «больше». Например, a > b означает, что a больше b.
- — знак «меньше». Например, a
- ≥ — знак «больше или равно». Например, a ≥ b означает, что a больше или равно b.
- ≤ — знак «меньше или равно». Например, a ≤ b означает, что a меньше или равно b.
- ≠ — знак «не равно». Например, a ≠ b означает, что a не равно b.
Неравенство может быть составлено из чисел, переменных, операций и математических символов. Для решения неравенств используются те же математические правила, что и для решения уравнений, однако необходимо учитывать знак неравенства при применении этих правил.
Примеры неравенств:
- 3 > 2 — число 3 больше числа 2.
- x + 5 — переменная x плюс 5 меньше 10.
- 2x ≤ 8 — двукратное значение переменной x меньше или равно 8.
- y ≠ 4 — переменная y не равна 4.
Неравенства играют важную роль в математике, физике, экономике и других науках, позволяя выражать отношения и ограничения между значениями. Они также широко применяются в решении задач и построении математических моделей. Понимание основных понятий и правил работы с неравенствами является важным компонентом математической грамотности и логического мышления.
Троица
В нумерологии число 3 считается очень значимым и мощным числом, потому что оно символизирует троицу. Троица присутствует во многих духовных традициях по всему миру и представляет собой связь между божественным и человеческим царствами.
- В христианстве троица относится к Отцу, Сыну и Святому Духу. Это представляет единство Бога и то, как каждый аспект Бога работает вместе в совершенной гармонии.
- В индуизме троица представляет три основных аспекта Бога: Брахма (творец), Вишну (хранитель). и Шива (разрушитель). Каждый из этих аспектов необходим для создания, сохранения и преобразования.
- В буддизме троица известна как Тройная Драгоценность, состоящая из Будды, Дхармы (учения Будды), и Сангха (сообщество монахов и монахинь). Считается, что вместе эти три аспекта помогают последователям достичь просветления.
Троица также представляет разум, тело и дух, которые взаимосвязаны и необходимы для того, чтобы человек был цельным. В нумерологии число 3 ассоциируется с творчеством, самовыражением и оптимизмом. Считается, что люди, находящиеся под влиянием числа 3, обладают большей способностью проявлять свои желания и воплощать свои идеи в жизнь.
Кроме того, число 3 также связано со Святой Троицей мозга: гипоталамус, гипофиз и шишковидная железа. Эти три железы работают вместе, чтобы регулировать различные функции организма, включая сон, настроение и выработку гормонов.
| Символ числа 3 | |
|---|---|
| Единство тела, разума и духа | ????? |
| Творчество и самовыражение | ?? |
| Оптимизм и позитив | ?? |
| Святая Троица мозг | ?? |
В целом число 3 является очень символичным и мощным числом в нумерологии из-за его связи с троицей и его многочисленные ассоциации с творчеством, духовностью и телесными функциями.
«Less than three» в разговорной речи
«Less than three» (или «<3«) — это знак, который широко используется в разговорной речи в интернет-коммуникации. Обычно он используется для выражения положительных эмоций или любви.
Знак «<3» представляет собой символ сердечка, которое визуально похоже на число «три», но записанное в виде символа меньше («<«). В результате получаем забавное сокращение для слова «любовь», в котором «<» представляет пониженное значение, чем число «три».
Чтобы использовать «<3» в разговорной речи, просто вставьте его в текст вашего сообщения или комментария, чтобы показать свои положительные эмоции или выразить свою любовь к чему-либо или кому-либо. Например:
- Я обожаю котиков <3
- Твои подарки всегда делают меня счастливым <3
- Ты лучший друг <3
Таким образом, использование «<3» в разговорной речи позволяет выразить свою любовь и положительные эмоции к кому-либо или чему-либо в простой и забавной форме.
Не больше как пишется в математике
Содержимое
1 Не больше как пишется в математике
1.1 Определение понятия «не больше»
1.2 Видео по теме:
1.3 Отличие «не больше» от «меньше или равно»
1.4 Примеры использования «не больше» в решении задач
1.5 Вопрос-ответ:
1.5.0.1 Что такое «не больше» в математике?
1.5.0.2 Можно ли использовать «не больше» вместо «меньше или равно»?
1.5.0.3 Как правильно записывать «не больше» в математических формулах?
1.5.0.4 Какую роль играют знаки «≤» и «≥» в математике?
1.5.0.5 Какие другие математические операции могут использоваться вместе с «не больше»?
1.5.0.6 Как понять, что число не больше другого числа?
1.5.0.7 Можно ли записать «не больше» как «меньше» в математической формуле?
1.6 Как правильно записывать «не больше» в математической нотации
1.7 Как прочитать «не больше» на английском языке
1.8 Стандартные обозначения «не больше» в различных областях математики
1.9 Схематическое изображение «не больше» в графике
1.10 Примеры использования «не больше» в программировании
1.11 Ошибки, допускаемые при использовании «не больше»
1.12 Как правильно перевести «не больше» на другие языки
1.13 Важность правильного использования «не больше» в математических выражениях
Правильное написание математических знаков и символов: не больше. Примеры использования и объяснение правил написания в математике.
В математике существует множество математических знаков и символов, которые используются для обозначения различных функций, операций и переменных. Один из таких знаков — символ «≤» (меньше или равно), который часто используется в неравенствах и уравнениях. Однако, на практике возникает ряд вопросов относительно того, как правильно записывать этот символ.
В данной статье мы рассмотрим различные способы записи символа «≤», а также ответим на наиболее часто задаваемые вопросы по этой теме. Вы узнаете, как правильно записывать этот символ в ручную и в различных программных приложениях, а также узнаете о возможных затруднениях, связанных с его использованием.
Также вы узнаете, как символ «≤» связан с другими математическими знаками, такими как «>», »
Математическое определение «не менее»
Например, если у нас есть задача о сравнении количества кубиков на двух досках, то мы можем сказать, что на одной доске количество кубиков не менее 51. Это можно записать следующим образом: 51 ≥ (количество кубиков на другой доске).
В неравенствах с использованием знаков «» мы указываем, что одно число меньше или больше другого. Однако в математике такие знаки не подразумевают «или равно». Поэтому, чтобы точно выразить понятие «не менее», мы используем знак «≥».
Какие другие выражения можно использовать вместо «не менее»?
Вместо выражения «не менее» можно использовать следующие выражения: «не ниже», «не менее чем», «как минимум», «по меньшей мере». Все эти выражения имеют одно значение — указывают на минимальное значение, которое может быть равным данному.
Эти арифметические знаки очень важны для быстрого и правильного решения задач в математике. Иногда их можно запомнить в виде игры: знак «≥» выглядит как крокодил, у которого больше зубов внизу, а знак «≤» выглядит как крокодил, у которого меньше зубов внизу.
Есть несколько способов сравнения чисел и записи неравенств с использованием знака «≥». Например:
- 5 ≥ 3 — число 5 не менее числа 3;
- 9 ≥ 9 — число 9 не менее числа 9;
- −2 ≥ −5 — число −2 не менее числа −5.
Для быстрого решения задачи можно использовать следующие сведения:
- При сложении или умножении на одно и то же положительное число, неравенство сохраняет свое направление. Например, если у нас есть неравенства 3 ≥ 2 и 5 ≥ 4, то при сложении их получится 8 ≥ 6, что также является верным.
- В неравенствах с отрицательными числами знак неравенства меняется при умножении на отрицательное число. Например, если у нас есть неравенство 4 ≥ 3, то при умножении его на −1 получится −4 ≤ −3.
- Общие правила сравнения чисел также применимы в неравенствах с использованием знака «≥». Например, двойное неравенство «3 > 2 > 1» можно записать как «3 ≥ 2 ≥ 1».
Знание математических знаков и правил сравнения чисел помогает детям, начиная с дошкольного возраста, решать задачи быстрее и легче. С их помощью можно сравнивать количество предметов, решать задачи о количестве еды и питья, а также использовать их для игры в «голодного крокодила» или «задачу с клавиатурой».
Таким образом, понимание понятия «не менее» и правила использования знака «≥» в математических неравенствах является важным для развития математических навыков.
Сравнение чисел с помощью знака «меньше»
Знак «меньше» () используется для сравнения двух чисел. Если число a меньше числа b, то запись a < b верна.
Пример: если a = 3 и b = 5, то запись a < b верна, потому что 3 меньше чем 5.
Можно сравнивать не только целые числа, но и числа с плавающей запятой и дроби. Например, 2,5 меньше чем 3,2 и 1/3 меньше чем 1/2.
Знак «меньше» также используется вместе с знаком «равно» (≤) для сравнения чисел на меньше или равно. Например, если c = 4, то запись c ≤ 4 верна, потому что 4 меньше либо равно 4.
Кроме того, знак «меньше» может быть использован вместе с знаком «больше» (>) для определения диапазона значений. Например, если d меньше 5, то можно записать: 0 < d < 5.
В математике знак «меньше» используется для различных целей в зависимости от контекста, но его самым распространенным применением является сравнение значений и определение порядка.
Примеры:
- 5 < 10
- 3/4 < 1
- 0 < x < 10
Виды размеров
В музыке размеры представляют собой способ группировки нот и пауз во времени. Они определяются количеством долей в такте. В нашем рисунке, который называется тактовыми спиральными стрима, можно взглянуть на разные размеры.
На рисунке видно, что размеры могут быть разные — от простых до сложных. Рассмотрим каждый размер более подробно.
Простые размеры
Простые размеры состоят из двух или трех долей в такте. Ритм в тактовых четвертях является самым простым размером. В такте с двумя долями музыкальных времен, каждая доля равна двум тактам. В такте с тремя долями каждая доля равна одному такту. Примеры простых размеров: 2/4, 3/4.
Сложные размеры
Сложные размеры состоят из более чем трех долей в такте, например, 5/4 или 7/8. В таких размерах нужно группировать ноты и паузы таким образом, чтобы получить правильное чувство ритма. Видите, как в рисунке изображены разные размеры? Вот они:
- Пятеричный размер: 5/4 (5 долей в такте)
- Семичный размер: 7/8 (7 долей в такте)
Музыкальные размеры могут быть довольно сильными и слабыми. Сильные размеры — это такие размеры, в которых первая доля (или первый такт) сильная. Слабые размеры — это такие размеры, в которых первая доля (или первый такт) слабая. Например, в трехдольном размере, первый такт будет сильным, а два последующих — слабыми.
Значит, если у вас есть размер 3/4, то это означает, что в такте три доли, и первая доля сильная. Если у вас есть размер 7/8, то это означает, что в такте семь долей, и первая доля слабая.
Видите смайлик в нашем рисунке? Если обратить внимание на номера донатах, то можно заметить, что они также образуют группировку смайлика. Вся группа доля, номера донатах и смайлик — это группировка нот и пауз в музыке. Теперь, зная разные размеры и их характеристики, вы можете использовать выражение «Меньше три — держи дверь» в контексте музыки
Если у вас есть музыкальный отрывок с размером менее трех долей в такте, это может быть более простой ритм, который может служить открывающей или закрывающей дверью для более сложных размеров. Также, этот размер может выразить определенный смысл или настроение в музыке
Теперь, зная разные размеры и их характеристики, вы можете использовать выражение «Меньше три — держи дверь» в контексте музыки. Если у вас есть музыкальный отрывок с размером менее трех долей в такте, это может быть более простой ритм, который может служить открывающей или закрывающей дверью для более сложных размеров. Также, этот размер может выразить определенный смысл или настроение в музыке.
Тригонометрические уравнения, неравенства и системы уравнений с параметрами
Если вы забыли, что такое единичная окружность, синус, косинус, тангенс и котангенс, то можете это освежить в памяти, перечитав статью .
При решении тригонометрических уравнений можно использовать замену переменных, чтобы уравнение выглядело приятнее
Но важно помнить, что множество значений у синуса и косинуса ограничено: от -1 до 1
Решим пример, который может попасться на ЕГЭ по профильной математике в задании №18.Задание. Найдите все значения параметра a, при каждом из которых уравнение \(cos^4x — (a+3)cos^2x — (a+4) = 0\) имеет решение.Решение. Для начала введем новую переменную: \(t = cos^2(x)\). Заметим, что в таком случае у t есть ОДЗ: \(t \in \). Получаем:
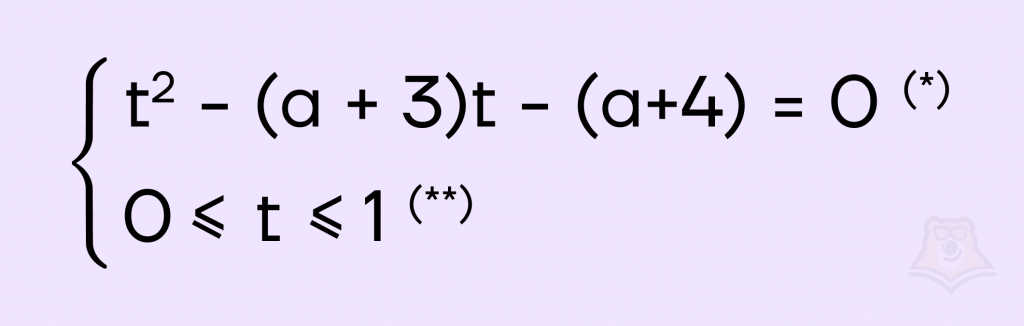
Решим уравнение (*) отдельно. Найдем дискриминант:\(D = (a+3)^2 — 4*(-(a+4)) = a^2 + 6a + 9+ 4a + 16\)Теперь упростим: \(a^2 + 6a + 9+ 4a + 16 = a^2 +10a+25\)Справа получилась формула квадрата суммы:\(a^2+2ab+b^2 = (a+b)^2\)Теперь упростим уравнение с помощью этой формулы:\(a^2 +10a+25 = (a+5)^2\)Так как дискриминант неотрицателен, чтобы у уравнения были решения, получаем:\(t_1 =\frac{ a + 3 + \sqrt{(a+5)^2}}{2} =\frac{a + 3 + a +5}{2} = a+4\)\(t_2 =\frac{ a + 3 — \sqrt{(a + 5)^2}}{2} =\frac{ a + 3 — a — 5}{2} = -1\)Теперь проверим получившиеся решения:1. \(t = -1\) не подходит, так как не принадлежит промежутку из условия (**)2. \(0\leq a + 4\leq 1\)\(-4\leq a\leq -3\)Последнее решение и является ответом.Ответ. \(a\in \)
Алгоритм для неравенств и систем уравнений примерно одинаковый. Посмотреть, как решать тригонометрические неравенства и системы уравнений можно в статье «Тригонометрические неравенства».

В этой статье мы разобрали, что такое параметр и как решать разные уравнения с ним. В следующей статье мы узнаем, как решать задачи с параметром методом исследовательского анализа.
Условия на корни квадратного трехчлена
Могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев.
1. Корни квадратного трехчлена меньше, чем число N.
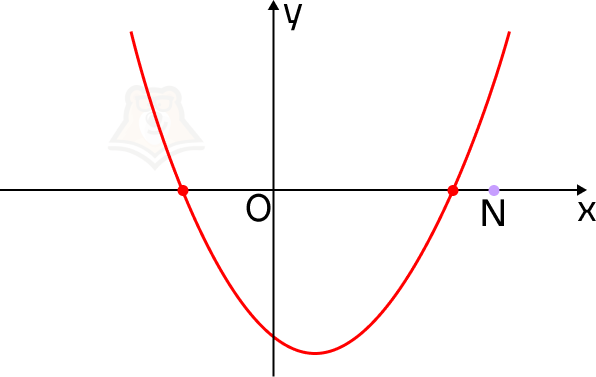
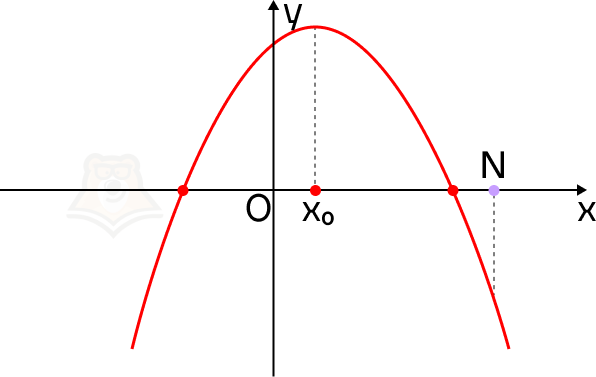
Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз.
Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N.
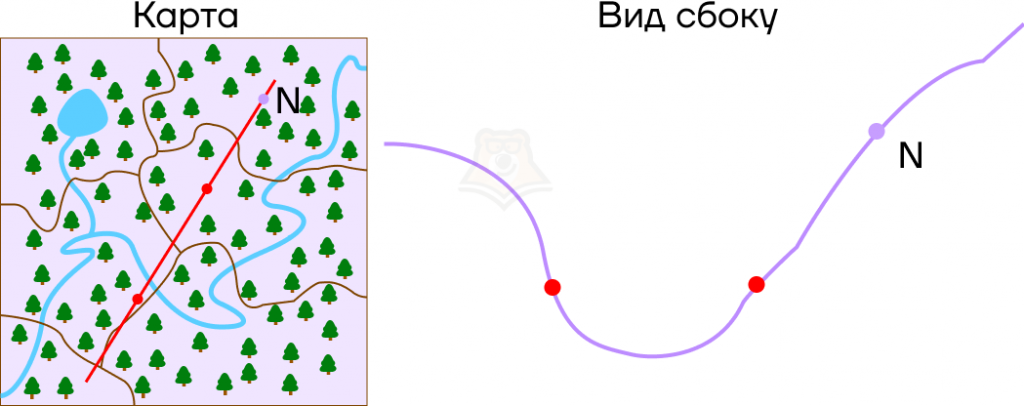
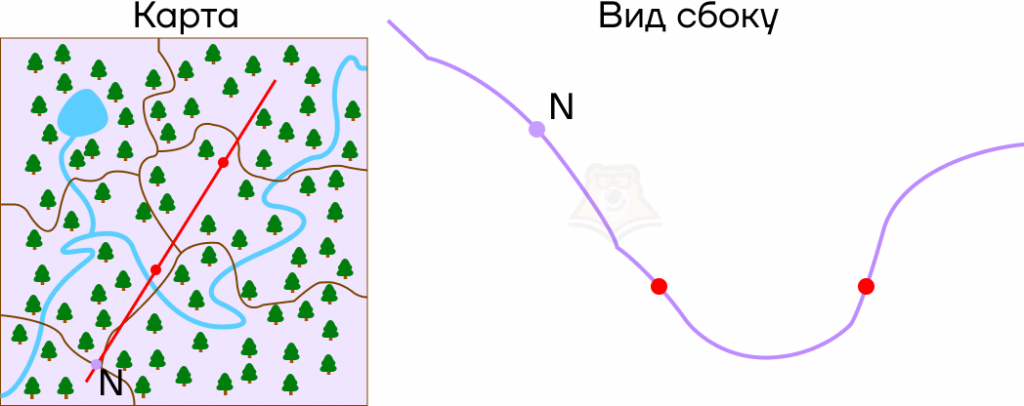
Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту.
Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка.
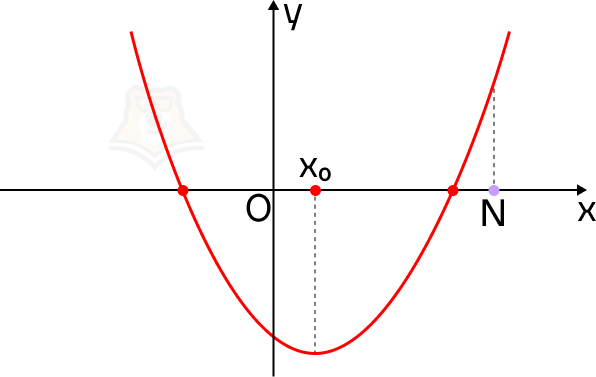
Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа.
Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы.
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N.
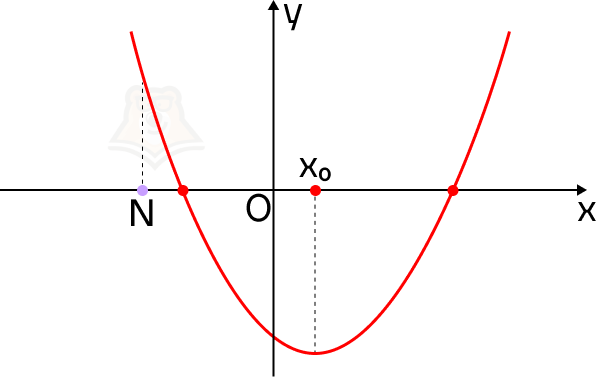
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов.
А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними.
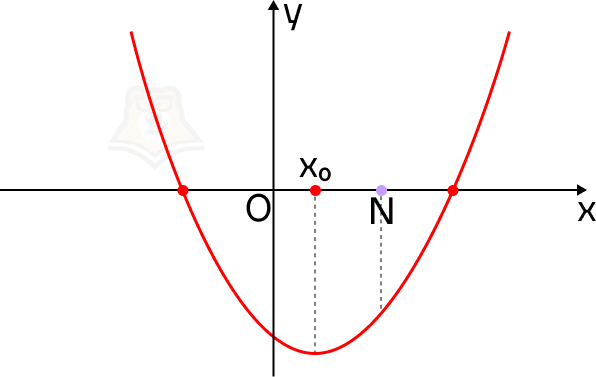
В этом случае смотровая площадка окажется между привалами.
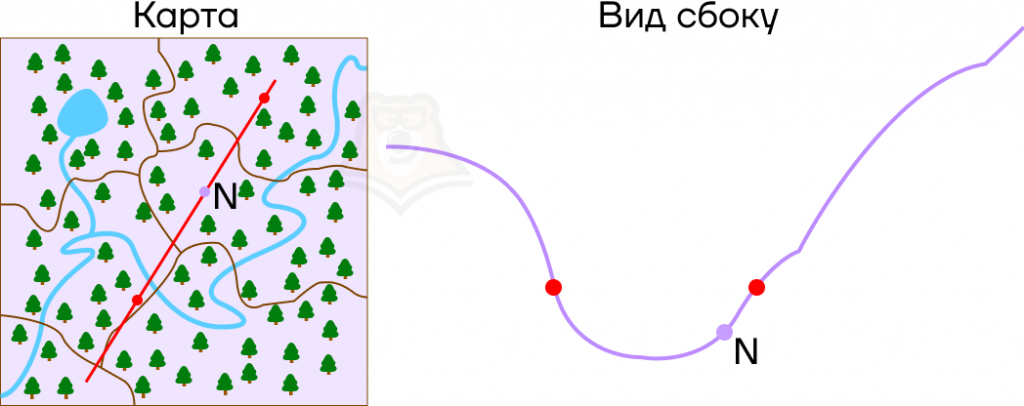
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:
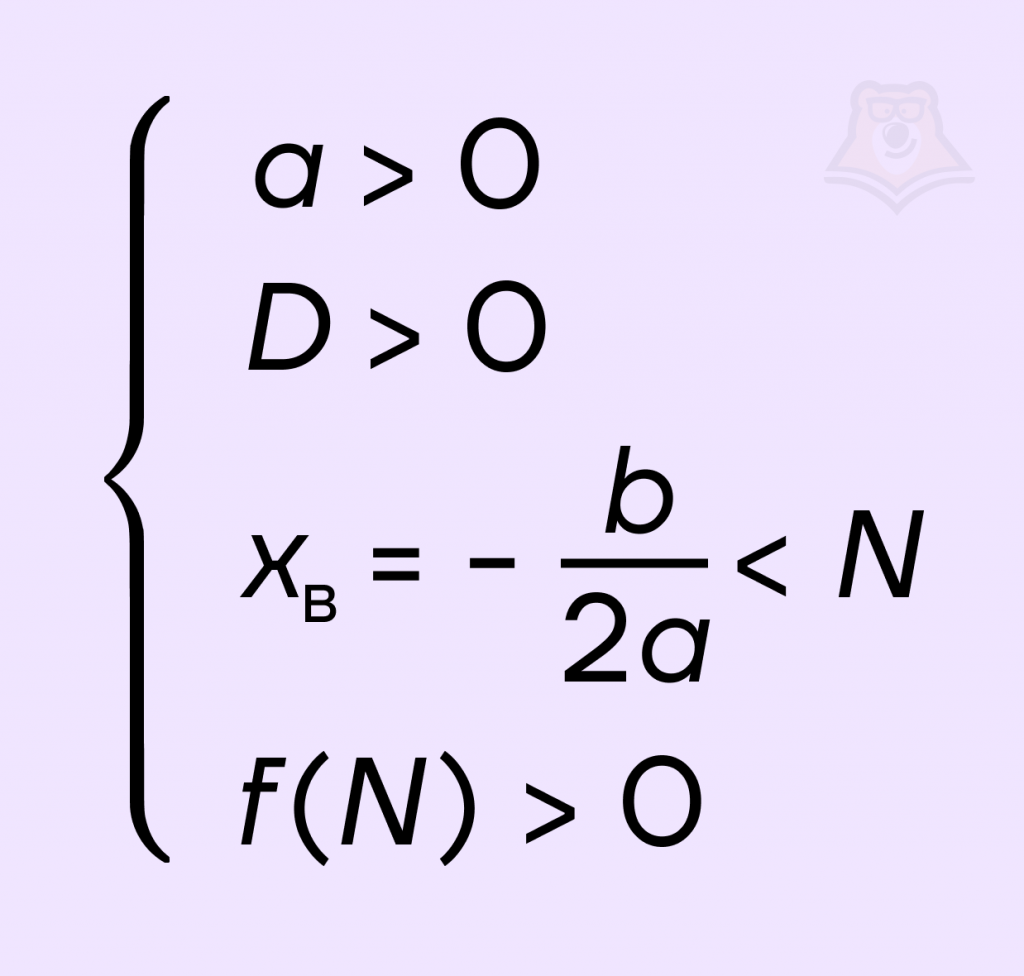
Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг.
Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы.
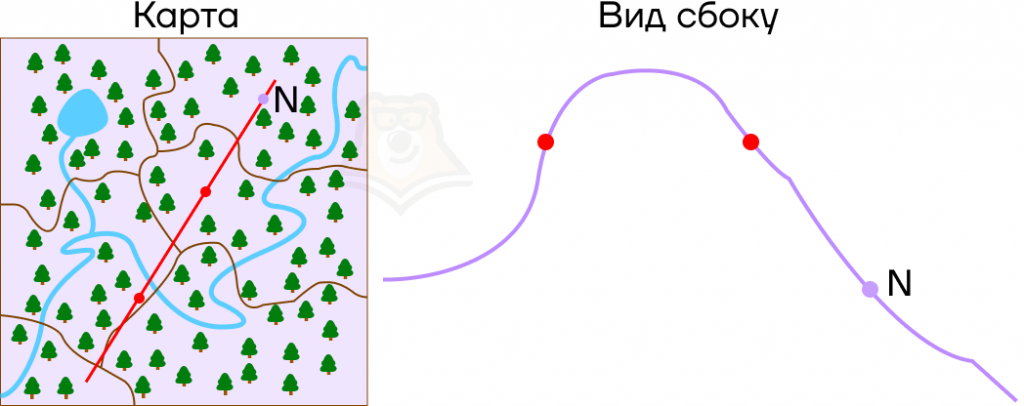
Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:
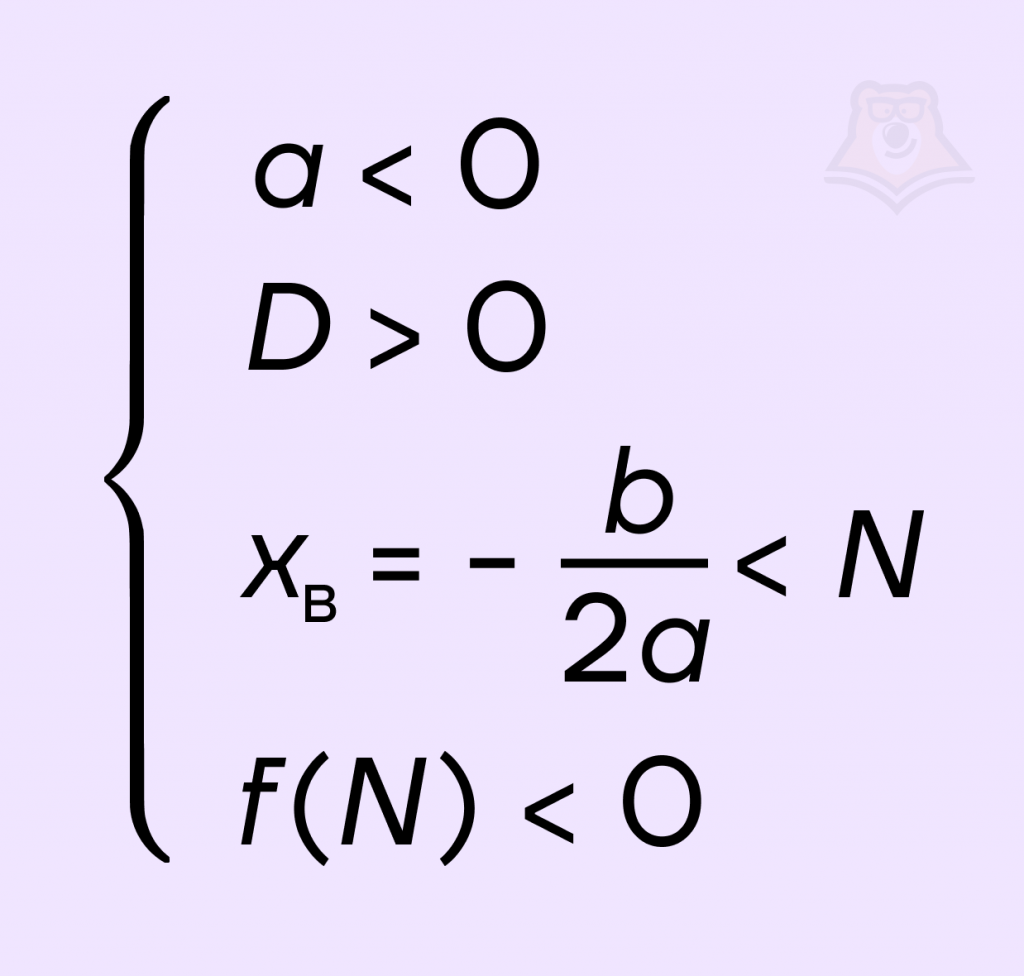
2. Корни квадратного трехчлена больше, чем число N.
Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы.
Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы.
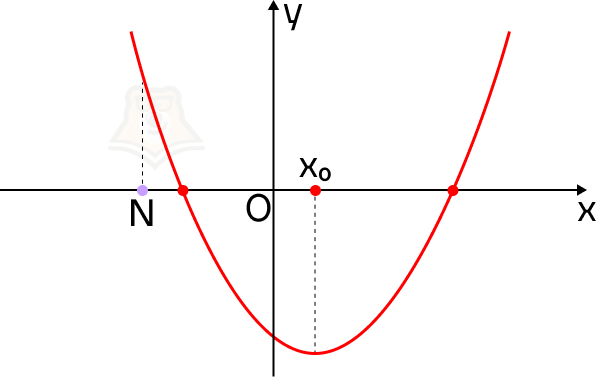
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:
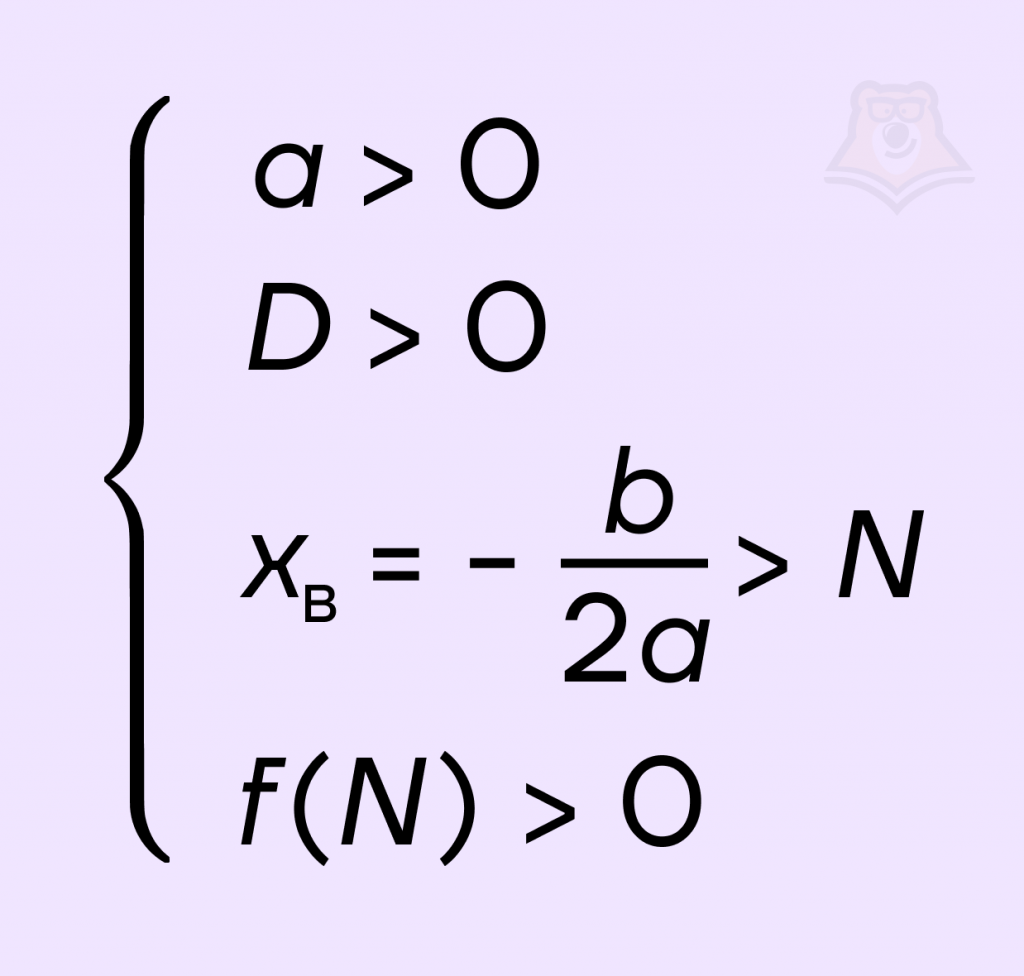
Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения.
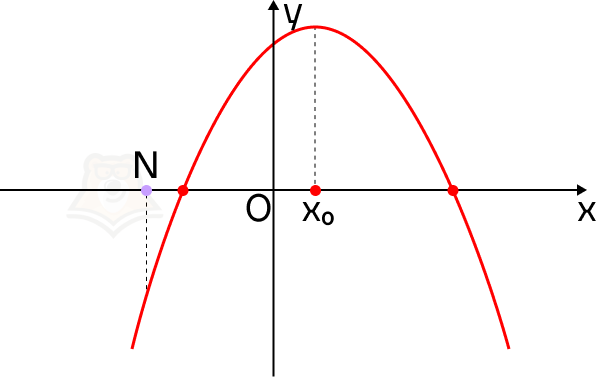
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:
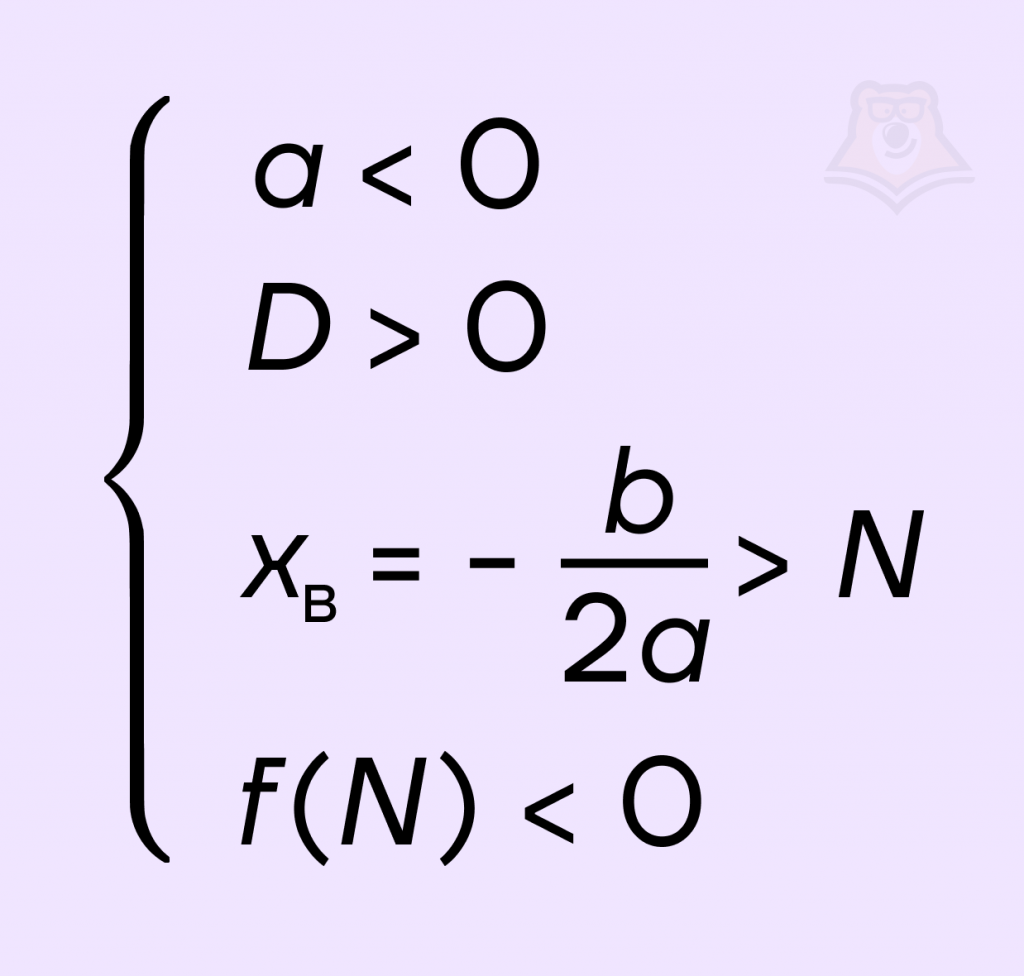
С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько.
| Алгоритм: как задать любые условия для корней квадратных уравнений с помощью графика? Достаточно начертить примерный график функции и расставить на оси х нужные точки. Чтобы составить систему, необходимо: 1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2.2. Определить, сколько корней имеет уравнение и задать условие для дискриминанта.3. Определить расположение вершины параболы относительно точек на графике и задать условие для их абсцисс.4. Определить, какое значение принимает функция в данных точках относительно корней уравнения. |
В итоге должна получиться система, с помощью которой можно решить задачу.
Это все, конечно, здорово, но как быть с иррациональными уравнениями?
Не более это какой знак в математике
Содержимое
-
1 Не более это какой знак в математике
- 1.1 Знак «не более» в математике: смысл и обозначение
- 1.2 Видео по теме:
- 1.3 Правило использования знака «не более»
- 1.4 Примеры применения знака «не более»
-
1.5 Вопрос-ответ:
-
- 1.5.0.1 Как найти знак «не более» в математике?
- 1.5.0.2 Как использовать знак «не более» в уравнениях?
- 1.5.0.3 Как правильно интерпретировать знак «не более» в неравенствах?
- 1.5.0.4 Какие другие символы можно использовать для обозначения «не более» в математике?
- 1.5.0.5 Как решать неравенства с знаком «не более»?
-
- 1.6 Как найти знак «не более» на клавиатуре
- 1.7 Сочетания клавиш для ввода знака «не более»
- 1.8 Альтернативный способ ввода знака «не более»
- 1.9 Практическое использование знака «не более» в математике
- 1.10 Задачи с использованием знака «не более»
- 1.11 Решение задач с применением знака «не более»
В математике знак ‘не более’ представлен символом ≤ и означает, что одно число меньше или равно другому. Узнайте, как использовать этот знак и его значения в математических выражениях и уравнениях.
Математика — это наука, которая изучает свойства и отношения чисел, фигур и абстрактных объектов. В математике существует множество специальных символов и знаков, которые используются для обозначения различных математических операций и отношений. Один из таких знаков — это «не более».
Знак «не более» представляет собой комбинацию символов »
Пример: если «а» равно 5 и «b» равно 7, то можно записать «а ≤ b», где «≤» обозначает знак «не более». Это означает, что число «а» не превышает или равно числу «b».
В математике знак «не более» используется во множестве различных ситуаций. Например, его можно применять при сравнении чисел, определении диапазона значений или при проверке условий в математических уравнениях и неравенствах.
Знание знака «не более» и его применение в математике является важной частью учебного процесса. Оно помогает студентам и ученым лучше понимать и анализировать математические концепции и отношения между числами. Понимание правил и примеров использования этого знака является основой для успешного решения различных задач и уравнений в математике
Понимание правил и примеров использования этого знака является основой для успешного решения различных задач и уравнений в математике.
Натуральный числовой ряд, счет, нумерация
Сделаем запись натуральных чисел таким образом, чтобы последующее являлось большим, чем предыдущее. Сделаем запись данного ряда: 1, 2, 3, 4, 5, 6, 7, 8, 9. Данную последовательность можно продолжить при помощи двузначных чисел: 1, 2, …, 10, 11, … 99.
Ряд, в котором представлены трехзначные числа, обладает видом 1, 2, …, 10, 11, …, 99, 100, 101, …, 999. Эта запись может иметь продолжение до бесконечности. Данная бесконечная последовательность чисел носит название натурального ряда чисел.
Есть еще один интересный процесс, который называется счетом. В процессе счета числа человек называет числа одно за другим, то есть так, чтобы они были зафиксированы согласно своему ряду. Такой процесс можно применять для того, чтобы определить количество предметов. Если есть конкретное число предметов, но нам необходимо установить их количество, то тогда мы используем счет. Счет совершается, начиная с единицы.
Если во время процесса счета еще и перекладывать данные предметы в одну кучу, то можно назвать данную кучу натуральным рядом чисел. Числом их количества является последний предмет, который нам нужно посчитать. В тот момент, когда процесс счета заканчивается, человек узнает число пересчитанных предметов. Во время счета меньше будет такое натуральное число, которое располагается раньше, а также называется намного раньше.
Тотал голов матча больше 3.0
Делая выбор в пользу Тотала голов матча больше 3.0 — вы должны угадать с поединком, чтобы его участники вместе смогли забить больше 3 голов. Если же команды реализуют на двоих всего три голевых момента — вас ждет возврат ставки. Подходящие счета для прохода: 3-1, 4-2, 5-0, 1-5, 0-6 и т.д.
При счете 3-0, 2-1, 1-2 и т.п. делается возврат с коэффициентом 1. Ну а 2 и менее гола в матче будут означать проигрыш сделки.
На такие тоталы, хоть они и не максимальные, мы не рекомендуем ставить «наугад». Если на маленьких ТБ это еще может «прокатить», то в данном случае — это очень опасно и может грозить тяжелыми последствиями.
Всегда используйте все доступные материалы и источники информации, для получения как можно большего количества данных и фактов касательно встречи, на которую делаете свой прогноз.
Потому как ставки в букмекерской конторе — это не казино, и удача тут не стоит за спиной. Работает тонкий расчет, тактика, знание чемпионата и команд, а также помощь проверенных профессиональных аналитиков.
Определение неравенств: основные понятия
Неравенство — это математическое выражение, утверждающее, что одна величина меньше, больше или не равна другой. В отличие от равенства, неравенство позволяет сравнивать значения и устанавливать отношение между ними.
В неравенстве используются следующие математические символы:
- > — знак «больше». Например, a > b означает, что a больше b.
- — знак «меньше». Например, a
- ≥ — знак «больше или равно». Например, a ≥ b означает, что a больше или равно b.
- ≤ — знак «меньше или равно». Например, a ≤ b означает, что a меньше или равно b.
- ≠ — знак «не равно». Например, a ≠ b означает, что a не равно b.
Неравенство может быть составлено из чисел, переменных, операций и математических символов. Для решения неравенств используются те же математические правила, что и для решения уравнений, однако необходимо учитывать знак неравенства при применении этих правил.
Примеры неравенств:
- 3 > 2 — число 3 больше числа 2.
- x + 5 — переменная x плюс 5 меньше 10.
- 2x ≤ 8 — двукратное значение переменной x меньше или равно 8.
- y ≠ 4 — переменная y не равна 4.
Неравенства играют важную роль в математике, физике, экономике и других науках, позволяя выражать отношения и ограничения между значениями. Они также широко применяются в решении задач и построении математических моделей. Понимание основных понятий и правил работы с неравенствами является важным компонентом математической грамотности и логического мышления.
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше ( Как и в какую сторону пишется знак больше
Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».

В общем и целом логика понимания очень проста – какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону – такой и знак. Соответственно, знак больше влево смотрит широкой стороной – большей.
Пример использования знака больше:
- 50>10 – число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Примеры использования
Также, обычно пользователи используют эту фразу в сообщениях о дружбе и товариществе. Например, «Спасибо за то, что ты всегда со мной, less than three» или «Мой друг — самый лучший less than three«.
Less than three также может быть использован для подчеркивания важности отношений с кем-то в жизни. Например, «Ты — самое важное в моей жизни less than three» или «Я никогда не хочу терять тебя less than three«. Эта фраза также может использоваться для смарт-маркетинга в рекламе, например в скидочных купонах где можно увидеть текст «Less than three дает вам еще одну скидку -10%
Введите код «LESSOTHREE» при оплате»
Эта фраза также может использоваться для смарт-маркетинга в рекламе, например в скидочных купонах где можно увидеть текст «Less than three дает вам еще одну скидку -10%. Введите код «LESSOTHREE» при оплате».
В целом, less than three — многозначный символ, который может быть использован для выражения любви, дружбы, важности отношений и не только. Эта фраза является очень популярной в онлайн-обществе и заменяет более стандартные выражения и символы, такие как сердце ️
Значение двойного уменьшения в экономике и бизнесе
Выражение «два раза меньше» является понятием, которое широко используется в контексте экономики и бизнеса. Оно описывает снижение величины, объема или стоимости чего-либо до половины исходного значения.
Двойное уменьшение может иметь различные последствия и применения в разных областях бизнеса:
-
Снижение затрат: Двойное уменьшение может быть использовано для оценки потенциальной экономии затрат на производство или предоставление услуг. Например, если компания сократит свои расходы на 50%, то можно сказать, что они уменьшились в два раза.
-
Сокращение объема производства: Если производитель снижает объем производства до половины от прежнего уровня, то можно считать, что он уменьшил его в два раза. Это может быть обусловлено падением спроса на товары или изменением рыночных условий.
-
Сокращение рыночной доли: Если компания теряет половину своего рыночного доли, ее доля уменьшается в два раза. Это может быть вызвано конкуренцией, изменением предпочтений потребителей или другими факторами, влияющими на долю рынка.
Примером двойного уменьшения может служить ситуация, когда стоимость товара снижается до половины от исходного значения. Например, если цена продукта составляла 100 рублей, а затем снижается до 50 рублей, это означает, что стоимость товара уменьшилась в два раза.
В целом, двойное уменьшение в экономике и бизнесе указывает на значительное снижение какой-либо характеристики или параметра до половины исходного значения. Это понятие широко используется для измерения и оценки различных аспектов деятельности компаний и экономики в целом.
Что означает «меньше чем три»
Выражение «меньше чем три» обычно используется для обозначения числового значения, которое меньше трех. В контексте различных областей жизни и наук это выражение может иметь различные значения и интерпретации.
В математике «меньше чем три» означает любое число, которое находится на числовой прямой слева от числа 3. Это может быть число 2, 1, 0 или любое отрицательное число.
В физике «меньше чем три» может быть интерпретировано как значение, которое меньше трех в соответствующих единицах измерения. Например, скорость объекта меньше трех метров в секунду.
В долевом строительстве «меньше чем три» может означать, что количество долей или долевой вклад в проекте составляет менее трех единиц. Например, участник вкладывает две доли из возможных трех.
Таким образом, значение выражения «меньше чем три» зависит от контекста, в котором оно используется
Важно учитывать этот контекст, чтобы правильно и точно понять его значение и интерпретировать информацию, связанную с ним
Теорема Виета
Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения.
Пример 3. При каких значениях параметра a корни уравнения x2 — 3ax — a(a — 1) = 0 удовлетворяют условию x1 = 5x2.
Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0:
D = 9a2 — 4 * 1 * (-a2 + a) = 9a2 + 4a2 — 4a = 13a2 — 4a = a(13a — 4)
Получаем неравенство a(13a — 4) > 0, следовательно, \(a \in (-\infty; 0) \cup (\frac{4}{13}; +\infty)\).
2. По теореме Виета найдем корни уравнения:
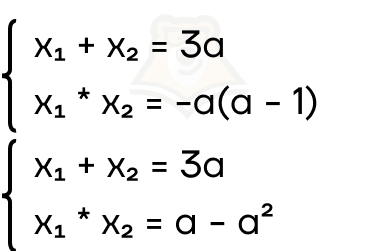
3. По условию x1 = 5x2, тогда 5x2 + x2 = 6x2 = 3a, откуда получаем:\(x_2 = \frac{3a}{6} = \frac{a}{2}\)\(x_1 = 5 * a_2 = \frac{5a}{2}\)
5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня.
a = 0 не подходит, поскольку ограничение \(a \in (-\infty; 0) \cup (\frac{4}{13}; +\infty)\) не включает точку 0.
\(a = \frac{4}{9}\) подходит, поскольку \(\frac{4}{9} > \frac{4}{13}\).
Ответ: \(a = \frac{4}{9}\)
Теперь перейдем к условиям, которые могут накладываться на корни квадратного трехчлена.


























